基于驾驶员转向模型的共享控制系统
2022-08-01田彦涛赵彦博
田彦涛 赵彦博 谢 波
众所周知,自动驾驶分为5 个阶段,分别是辅助驾驶系统、部分自动驾驶、有条件的自动驾驶、高度自动驾驶、完全自动驾驶.有一部分专家跳过人机共享控制的过程,直接对无人驾驶进行研究,2013 年,姜岩等[1]提出基于微分约束的横纵向协同规划算法,用高阶多项式模型在预瞄距离内对可行驶曲线进行建模,横向规划算法提供横向安全性,纵向规划算法保证了纵向安全性,最终能够实现封闭环境下速度低于 40 km/h 的无人驾驶.2017 年,田涛涛等[2]提出了一种基于无模型自适应控制的无人驾驶汽车横向控制方案,其实际是运用了预瞄偏差角构成横向控制的数据模型,从而避免了对无人车复杂模型的建模,进而设计自适应算法,该方法对复杂的无人驾驶运行有较好的自适应性.一定环境条件限制下的无人驾驶研究得到了较快的发展,但是当前驾驶的现实情况下是无法忽略驾驶员的,则本文着重考虑人机共驾的共享控制过程.
共享控制的应用广泛,可应用于飞行领域、车辆驾驶领域、智能轮椅领域以及机器人等领域[3−8],以车辆驾驶为例,当前无人驾驶存在安全性和可靠性无法保障的问题时,共享驾驶在目前汽车行业发展过程中能够发挥其积极的作用[9−11].因此,在保证车辆行驶安全性的基础上,如何合理分配二者的驾驶权重以及优化共享系统的性能是共享控制的核心问题[12−14].2004 年,Griffiths 等[15]较早地针对人机共享控制问题展开研究并取得了一定的研究成果,其研究结果表明通过对驾驶员进行触觉辅助能够提高驾驶精度、减轻驾驶员负担,但是其未考虑当驾驶员与控制器发生控制冲突时,应该如何有效分配控制权.2016 年,Erlien 等[16−17]提出了基于模型预测的避障预测触觉反馈控制方案,系统引入安全驾驶包络的概念,使得系统能够包容不同的驾驶风格,大大降低了人机之间不必要的控制冲突.2018 年,Nguyen 等[18]提出了一种新的共享控制方法用于车道保持系统,该方法能够合理地分配驾驶员与控制器的驾驶权,并且能够有效降低两者之间的冲突,但其缺乏对驾驶员不同驾驶状态下的人机共享的讨论.2019 年,Ji 等[19]提出了一种基于随机博弈的共享控制框架,从而有效地模拟驾驶员与智能系统之间的转向力矩,该框架下博弈的合理性得到了有效的验证.本文则从驾驶员的角度出发,在并联方式的间接共享控制的结构下,建立驾驶员转向操控模型,并利用遗传算法辨识驾驶员模型参数,可以得到一个与驾驶员特性相近的模型,其合理性得到验证,在辨识出相关参数后,将其作为共享控制器应用至共享控制系统,同时对驾驶员不同驾驶状态下的人机共享控制作进一步分析,从而能够得到该模型能够有效增加驾驶精度,减轻驾驶员的驾驶负荷.本文的主要贡献有:1) 针对驾驶员转向模型的参数辨识问题,本文采用遗传算法对驾驶员转向模型的视觉预瞄参数、补偿参数与神经肌肉系统参数进行辨识,获得了很好的拟合效果;2) 针对车辆与道路曲率变化对驾驶员模型参数的影响,本文基于上述辨识方法进一步分析不同车速和道路曲率下驾驶员模型参数的变化情况,并建立了驾驶员神经肌肉系统相关参数与车速之间的函数关系,以达到增加驾驶员模型参数适用范围的目的;3) 针对驾驶员不同驾驶状态下的人机共享问题,本文将已辨识的理想驾驶员模型应用至共享系统,并基于模拟驾驶实验平台对共享系统进行在线实验,实验结果说明该系统能够在不同的驾驶员转向操作下保证车辆行驶的安全性与轨迹跟踪的精确性,同时能够减轻驾驶员的驾驶负荷.
本文结构安排如下:第 1 节对驾驶员转向行为进行描述并对驾驶员转向行为进行建模;第 2 节分别对实验场景与驾驶员状态信息进行采集,并对第 1节得到的驾驶员转向模型进行参数辨识;第 3 节给出仿真实验结果,并对结果进行分析;第 4 节得出结论.
1 驾驶员转向模型建立
借鉴文献[20]并联方式的间接共享控制结构,如图1 所示,驾驶员与控制器分别作用于转向角权重分配,综合作用于车辆.
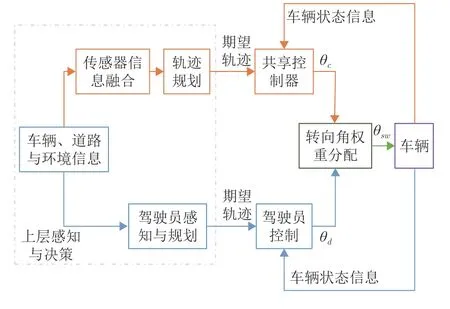
图1 间接共享控制结构图Fig.1 Indirect shared control structure
1.1 视觉预瞄、补偿与传递延迟
本文使用基于两点预瞄特性与神经肌肉系统的驾驶员转向模型结构[21],主要包括视觉预瞄模块、视觉补偿模块和神经肌肉模块,如图2 所示.该模型可简化为两点预瞄模型[22],如图3 所示.图3 中近预瞄点用来计算车辆与道路中心线的偏差距离,远预瞄点用来估算前方道路的曲率大小.在图3 中,lf代表远预瞄点与车辆距离,ln代表近预瞄点与车辆距离,Rt代表转弯中心到远预瞄点的距离,Rv代表车辆的转弯半径;因此可以得到,远预瞄点处的偏差角θf与近预瞄点处的偏差角θn可表达为[22]
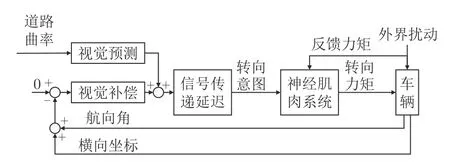
图2 驾驶员转向结构示意图Fig.2 Driver steering structure

图3 驾驶员两点预瞄示意图[22]Fig.3 Two-point preview of driver[22]

式 (2) 中,预瞄侧向偏差为yL,车辆航偏角为φL,θf是视觉预测模块Gp的输入,θn是视觉补偿模块Gc的输入,Gp和Gc分别表达为[22]
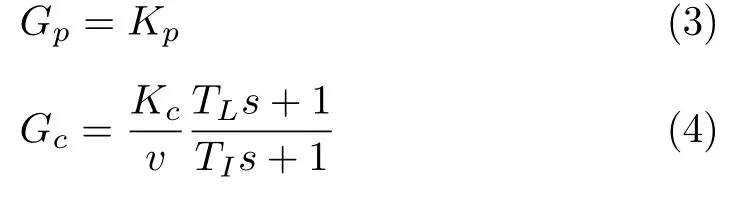
其中,预测模块的比例增益为Kp,补偿模块的比例增益为Kc,车辆行驶速度为v,补偿速率为TL,补偿频带为TI.时间延迟可以用纯滞后环节 e−τps进行表达,为提高模型的通用性,对此采用一阶泰勒近似,即

延迟模块作用于神经肌肉系统,进而通过神经肌肉系统作用于方向盘,因此,接下来需要对神经肌肉系统进行建模与分析.
1.2 神经肌肉模型
本文借鉴了英国剑桥大学的 Pick 等[23−24]的肌电分析方法得到了肌电信号与转向力矩的关系,以及清华大学刘亚辉等[25]提出的驾驶员神经肌肉收缩以及物理变化过程的一些研究结论,从而搭建神经肌肉系统的传递函数模型.该模型由前馈GNa、反馈GNf与神经肌肉动力GNM三个部分构成,如下所示[22]:
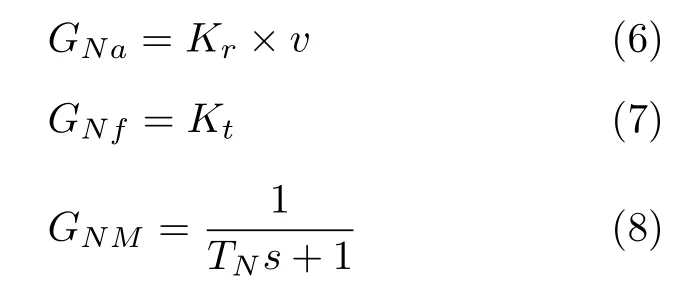
其中,Kr是力矩与转角间的比例系数;v是车辆的纵向速度;TN是神经肌肉的时间因子;Kt是转向角偏差的比例因子.综上所述,驾驶员模型的传递函数如图4.其中代表驾驶员意图产生方向盘转角,δsw代表反馈的方向盘转角,Γs代表反馈力矩,Γd代表模块输出力矩.为了方便参数辨识过程,将驾驶员模型的传递函数改写为驾驶员转向模型的状态空间形式:
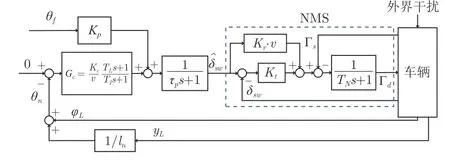
图4 驾驶员转向模型Fig.4 Driver steering model

其中,x1,x2,x3是传递函数转换成状态空间过程中产生的中间变量,是输入输出之间的一种线性组合.
2 参数辨识
2.1 实验场景与驾驶员状态信息采集
本文着重考虑转弯时的转向特性,建立双向单车道如图5 所示,其中,路面坡度为 0,附着系数设为 1,长度为 3 m,两线间隔为 6 m,单侧道路宽度为 3.5 m.

图5 模拟驾驶实验场景Fig.5 Driving simulation experiment scenario
道路的俯视图如图6 所示,由直线段和半径分别为200 m、300 m 的 90°弯道组成实验道路,采用内置的车辆模型,由于现有的设备与方法还暂时无法检测出驾驶员视觉感知的远预瞄点和近预瞄点误差的真实值,因此,根据文献[22]的论述,本文选取车辆前方行驶路径中心 5 m 远处为近预瞄点,车辆前方道路间隔线 10 m 远处为远预瞄点.其次,为了便于模型参数的辨识,本文将每次实验中车辆的行驶速度v设定为常数.因此,实验时车速为 72 km/h,转弯半径为 200 m.

图6 模拟驾驶实验场景 (单位:m)Fig.6 Driving simulation experiment scenario (unit:m)
2.2 驾驶员转向模型参数辨识
为了研究驾驶员转向特性,只选取弯道路况数据,数据集截取各个变量 800~2 200 之间的 1 400个数据点,驾驶员力矩数据序列滤波后如图7 所示.

图7 驾驶员力矩滤波与截取Fig.7 Filtering and interception of driver torque
可以看出滤波后的曲线更加平滑.遗传算法与传统算法相比较具有能够求出优化问题的全局最优解、优化结果与初始条件无关、具有较强的鲁棒性和适合于求解复杂的优化问题等诸多优点,故本文选用遗传算法对模型参数进行辨识.
基于实验并结合文献[26]给出的参数大致取值范围,遗传算法的主要参数取值如表1 所示.

表1 遗传算法主要参数取值Table 1 Value of main parameters of genetic algorithm
将 8 个待辨识参数看作遗传基,采用实数编码方法,故可将其表示为
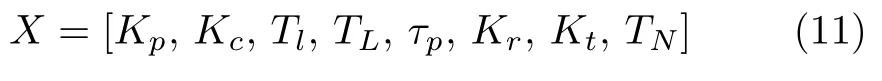
本文为了使驾驶员真实值与模型输出值的总体误差最小,将目标函数定义为误差函数的 1/2,即

其取值范围的上限与下限分别设置为

因为采集的数据为离散序列,式 (9) 和 (10) 的驾驶员模型数据变化是连续的,所以需要对采集数据进行离散处理,即

其中,I代表三阶单位矩阵,T0.02 s,代表采样周期.目标函数值在车速为 72 km/h 时的迭代寻优曲线如图8 所示,最小值为 0.891,驾驶员力矩的真实输出曲线与辨识模型输出曲线的拟合程度如图9所示.

图8 目标函数值(v=72 km/h,R=200 m)Fig.8 Value of objective function(v=72 km/h,R=200 m)

图9 驾驶员力矩测量值与辨识值对比(v=72 km/h,R=200 m)Fig.9 Comparison of measurement and identification value (v=72 km/h,R=200 m)
可以看出,驾驶员真实值的变化与最优个体的模型输出值的变化基本一致,则模型参数的最优个体取值为

为了更好地验证模型的准确性,截取第2 段弯道来验证模型性能,车速仍为 72 km/h,验证结果如图10 所示.

图10 驾驶员力矩测量值与模型输出值对比Fig.10 Comparison of measurement and model output value of driver torque
可以看出,驾驶员真实值与模型输出值变化趋势几乎一致.最大力矩误差值为 0.298 N·m,如图11所示,力矩误差的和方差SSE1.784,均方差MSE0.0013,均方根RMSE0.036.
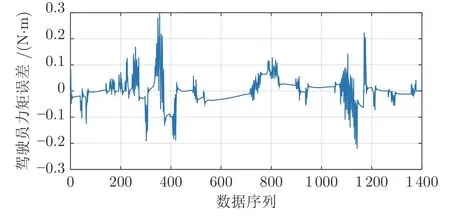
图11 驾驶员力矩误差值Fig.11 Error value of driver torque
为了进一步分析不同车速、道路曲率下驾驶员模型参数的变化情况,分别将转弯半径设为 200 m和 300 m,采集多组驾驶员在 54 km/h,63 km/h,72 km/h,90 km/h,108 km/h,126 km/h 下的参数变化情况,变化结果分别如表2 和表3 所示.

表2 转弯半径为200 m 的驾驶员模型参数Table 2 Driver model parameters with turning radius of 200 m
为了对数据进行更加直观的分析,将表2 和表3数据分别制作成图表的形式,如图12 和图13 所示,可以看出,车速和视觉补偿增益Kc是反比例关系,车速与驾驶员神经肌肉系统反馈刚度Kt是正比例关系.
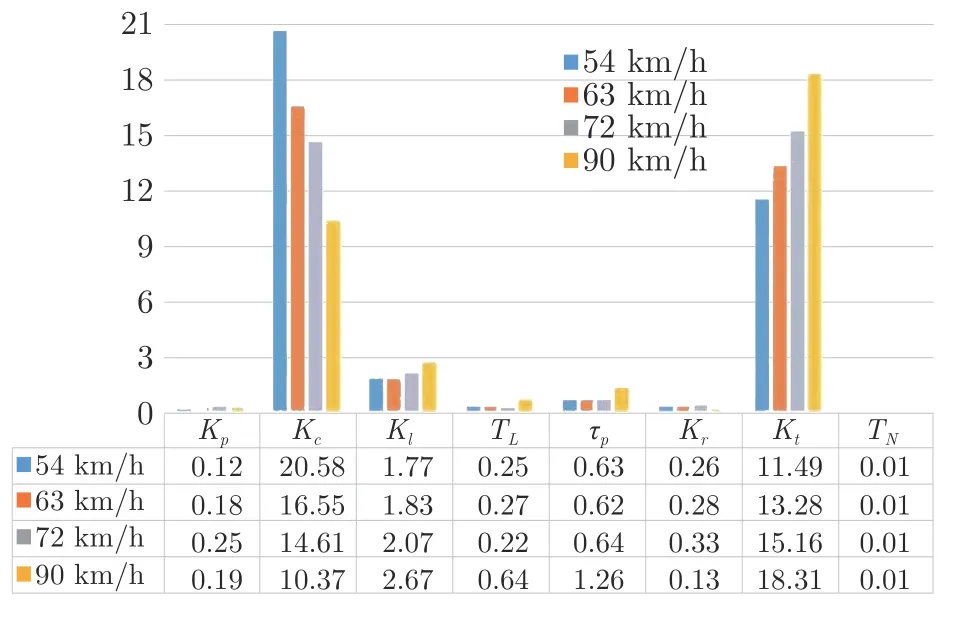
图12 不同车速下模型参数平均值对比(R=200 m)Fig.12 Comparison of mean values of model parameters at different vehicle speeds (R=200 m)
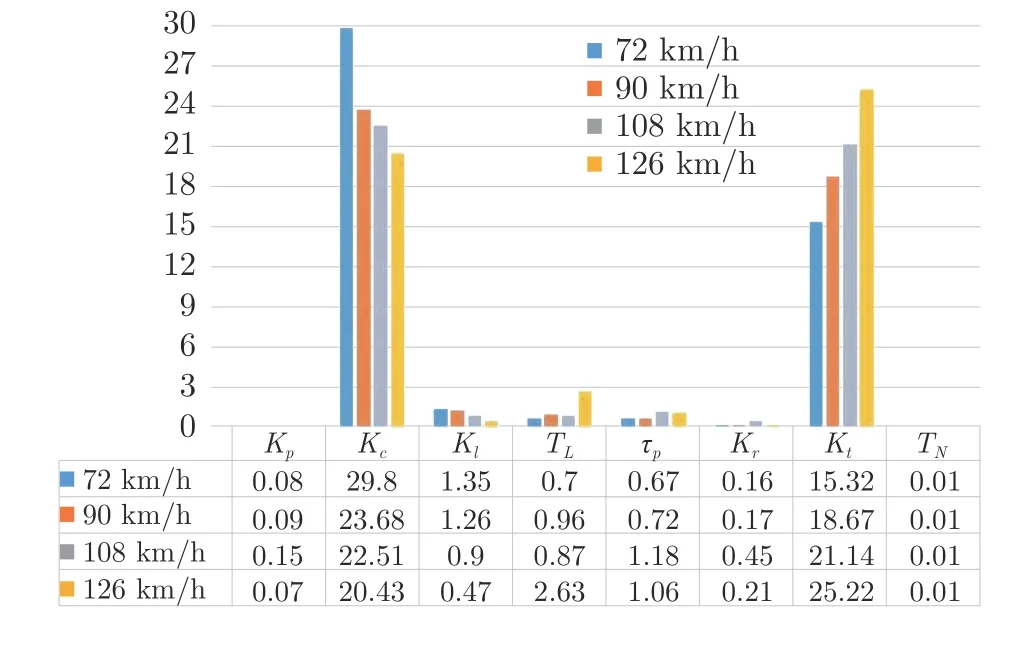
图13 不同车速下模型参数平均值对比(R=300 m)Fig.13 Comparison of mean values of model parameters at different vehicle speeds (R=300 m)

表3 转弯半径为300 m 的驾驶员模型参数Table 3 Driver model parameters with turning radius of 300 m
而车速分别在 72 km/h 和 90 km/h 且转弯半径不同的情况下,Kt无明显变化.另外Kr在当前实验情况下变化不明显,TN也基本保持不变,约为 0.01.可见转弯半径对参数变化影响不大.因此本文主要讨论Kt与速度的关系,相关参数的误差指标如表4和表5 所示.
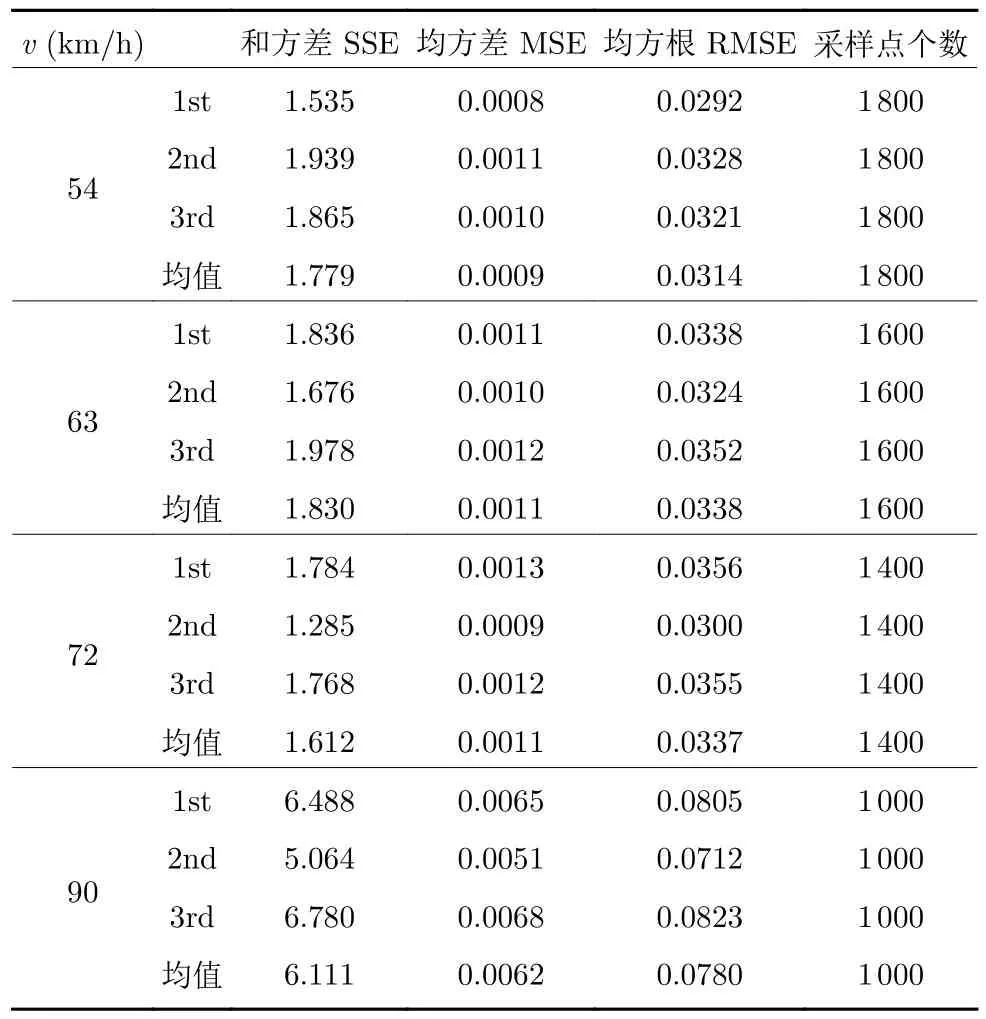
表4 驾驶员模型的辨识误差指标(R=200 m)Table 4 Identification error index of driver model (R=200 m)
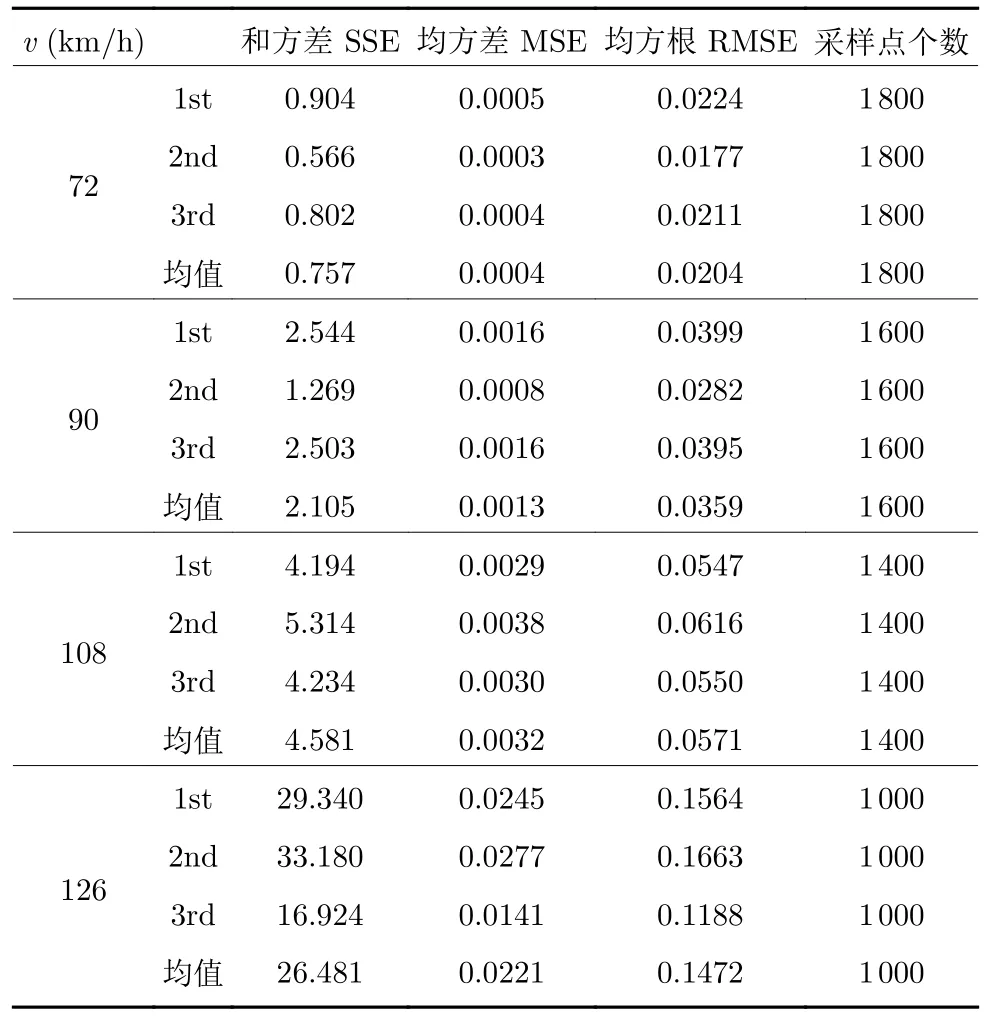
表5 驾驶员模型的辨识误差指标(R=300 m)Table 5 Identification error index of driver model (R=300 m)
当转弯半径为 200 m 时,利用Kt与车速v的数据进行一次曲线拟合.拟合范围即速度的变化范围,拟合函数如式 (18),拟合曲线如图14 所示.由图14 得,曲线的拟合精度达到 99.82%,和方差为0.045.
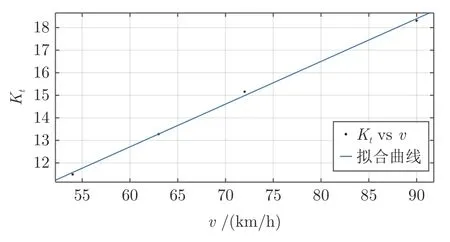
图14 转弯半径为200 m 时神经肌肉反馈刚度与车速的拟合曲线Fig.14 Fitting curve of K t and v at turning radius of 200 m

当转弯半径为 300 m 时,拟合函数如式 (19),拟合曲线如图15,曲线拟合精度达到 99.15%,和方差为 0.4432.可见式 (19) 的拟合度相对较低,这可能是由于参数辨识精度不高或模型的非线性造成的.

图15 转弯半径为300 m 时神经肌肉反馈刚度与车速的拟合曲线Fig.15 Fitting curve of Kt and v at turning radius of 300 m
由于在车速变化的情况下存在采样的数据点也在变化的问题,为了解决采样数据点变化的问题,本文采用数据的均方差和均方根误差来进行分析.如图16 所示,模型的辨识误差随着车速的增加而增加.同样也表明速度在 54~72 km/h 的范围内时,模型的辨识误差小,此时驾驶员的转向行为更加平稳.

图16 不同车速下驾驶员模型辨识误差指标对比(R=200 m)Fig.16 Comparison of driver model error index at different vehicle speeds (R=200 m)
当车速为 90 km/h 时,模型辨识误差显著增加,说明驾驶员的转向行为表现较差.图17 进一步验证了速度较高模型辨识误差大的结论.另外,随着转弯半径增大,会使模型辨识误差减小,即驾驶员的转向行为变得稳定.
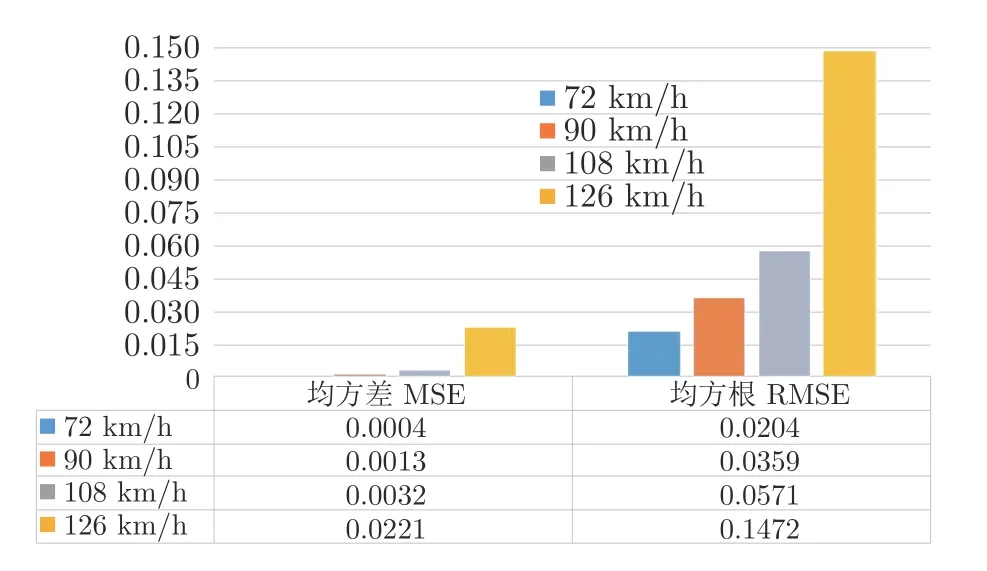
图17 不同车速下驾驶员模型辨识误差指标对比(R=300 m)Fig.17 Comparison of driver model error index at different vehicle speeds (R=300 m)
3 仿真实验与结果分析
这里沿用了文献[20]中所提出的模糊权重分配策略,该策略主要负责根据输入变量(横向偏离程度LD与转向角精确程度 Δφcd) 的变化实现转向角权重值的合理自适应分配.其变化规则如下:
1)LD相同时,控制器控制权随着转向角精确度的增加而逐渐减小;
2) 当控制器转向角更精确且转向角精确度相同时,LD越大控制器控制权越大;
3) 当驾驶员转向角更精确且转向角精确度相同时,LD越大控制器控制权越小;
4) 当控制器与驾驶员转向角相等,控制器控制权保持不变.
最终输出便是合理的权重分配系数,进而得到期望转向角,其具体表达为


其中,kc是控制器权重,kd是驾驶员权重.由此能够更好地验证驾驶员模型,并且能够有效地进行在线共享控制实验,获取相关特性.
3.1 理想驾驶员模型参数选取
驾驶员模型结构简单,辨识精度高,本文的目的是基于驾驶员转向模型设计共享控制器,以满足驾驶员与控制器共享控制的需求.因此,本文的理想驾驶员采用 CarMaker 的内置驾驶员模型.采集转弯半径为 200 m,车速分别为 54 km/h,63 km/h,72 km/h,83 km/h 和 94 km/h 时的理想转向数据,从而得到神经肌肉反馈刚度与车速的关系.选取车速为 72 km/h 时的理想驾驶员转向数据,并利用遗传算法辨识模型参数,驾驶员转向力矩的真实值与辨识值对比如图18 所示.

图18 辨识模型与真实测量转向数据对比Fig.18 Comparison of identification model and measurement value
可以看出,辨识力矩值的拟合程度非常高,且变化趋势基本一致,误差非常小,当前情况下的模型参数为

进一步选取车速为 54 km/h,63 km/h,83 km/h和 94 km/h 的理想数据,并得到相关评价指标,统计结果如表6 所示,显然Kt与车速之间呈近似正比例关系,根据曲线拟合方法,拟合范围为实验选取的速度范围,可得到二者的一次函数关系为
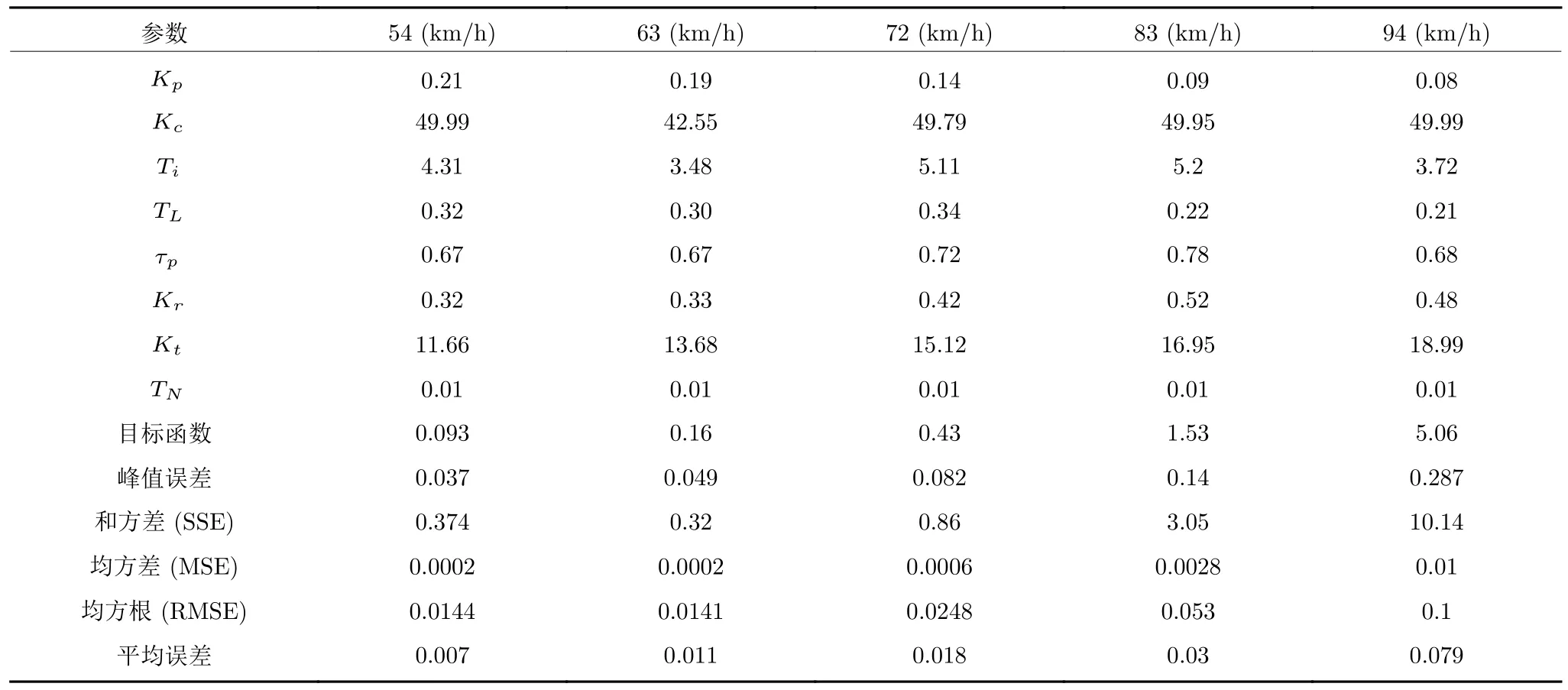
表6 不同车速下的驾驶员模型参数辨识结果Table 6 Identification of driver model parameters at different vehicle speed
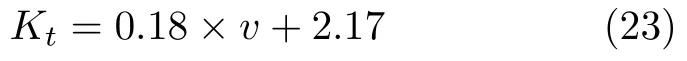
如图19 所示,拟合精度较高,因此,本文将利用包含车速的解析形式表示反馈增益Kt.
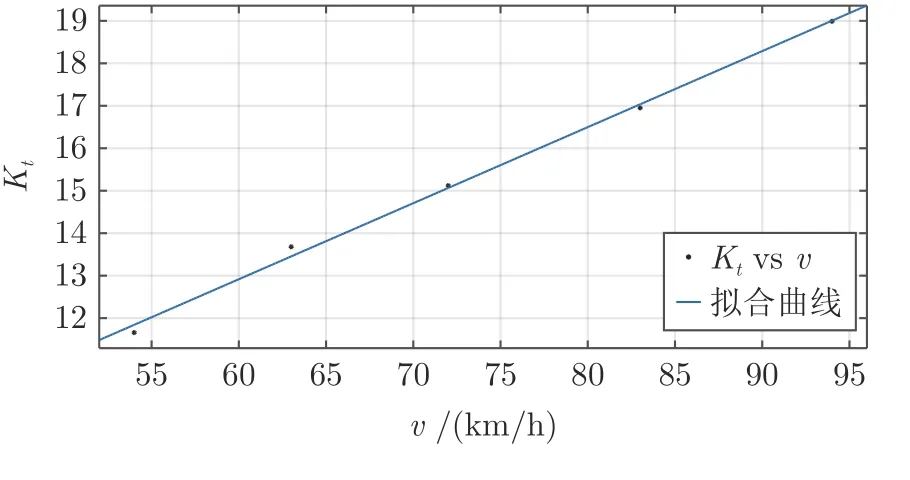
图19 数据点与拟合曲线Fig.19 Fitting curve and data point
由于本文驾驶员模型的输出为驾驶员力矩,所以需要建立转向系统模型,从而连接驾驶员与模糊权重分配模块.转向系统传递函数的形式为
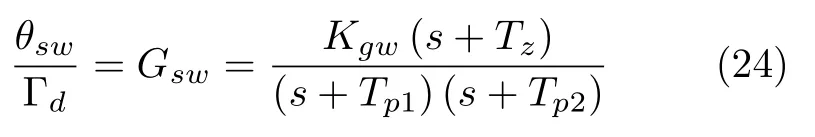
其中,Gsw代表转向系统的传递函数,Kgw代表模型增益,Tz代表函数零点,Tp1和Tp2代表函数极点.
转向系统模型参数的辨识结果如图20 所示,可以看出辨识精度较高,图21 进一步验证了模型的准确性.可见该模型能够有效描述转向系统,辨识后的模型可写为

图20 辨识模型值与真实测量值对比Fig.20 Comparison of identification model value and measurement value

图21 已辨识模型的输出值与真实测量值对比Fig.21 Comparison of the output value of the identified model with the measured value

其中,零点−0.298 与极点−0.31 非常接近,零极点抵消后的模型为
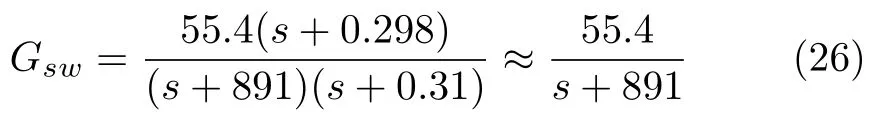
3.2 共享控制系统在线测试与评价
3.2.1 共享控制器单独驾驶测试
为了讨论控制器对于该模型的表现性能,首先则对控制器在不同的行驶速度下的转向性能进行实验检测.本文采用 Simulink 和 CarMaker 联合仿真的方式进行实验,采用 CarMaker 内置车辆模型,在 Simulink 中搭建控制器.实验结果如图22 所示,由于道路宽度为3.5 m,显然当车速为120 km/h时,车辆右侧已经驶出道路边界线,另外,当车速低于120 km/h 时,车辆能够有效通过转弯半径为200 m 的弯道.
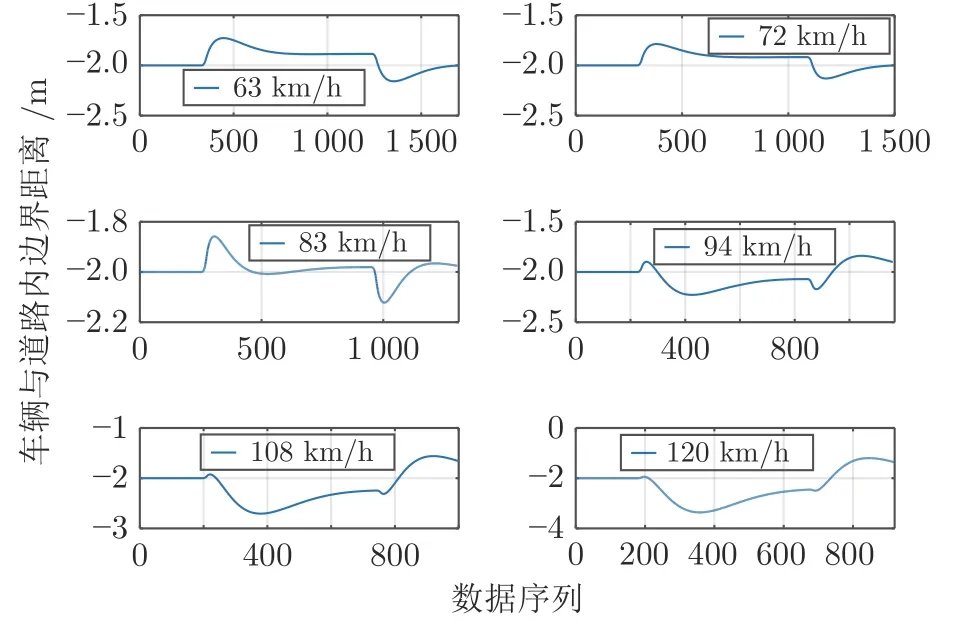
图22 不同车速下车辆中心点与道路内边界的距离Fig.22 Distance between vehicle center point and road internal boundary at different vehicle speeds
另外,从图23 看出模型输出力矩随着速度的增加而增加,从图24 看出方向盘转角也是随着速度的增加而增加,由此可以得出速度越快,控制器的控制力度越大,由此来保证车辆转弯的通过性与安全性.图25 得到不同车速下车辆的路径跟踪偏差,可以看到速度越快,路径跟踪的偏差越大,当车速小于 94 km/h 时,车辆的路径跟踪偏差都能够保持在一个较小的范围内.

图23 不同车速下共享控制器的输出力矩Fig.23 Output torque of shared controller at different vehicle speeds
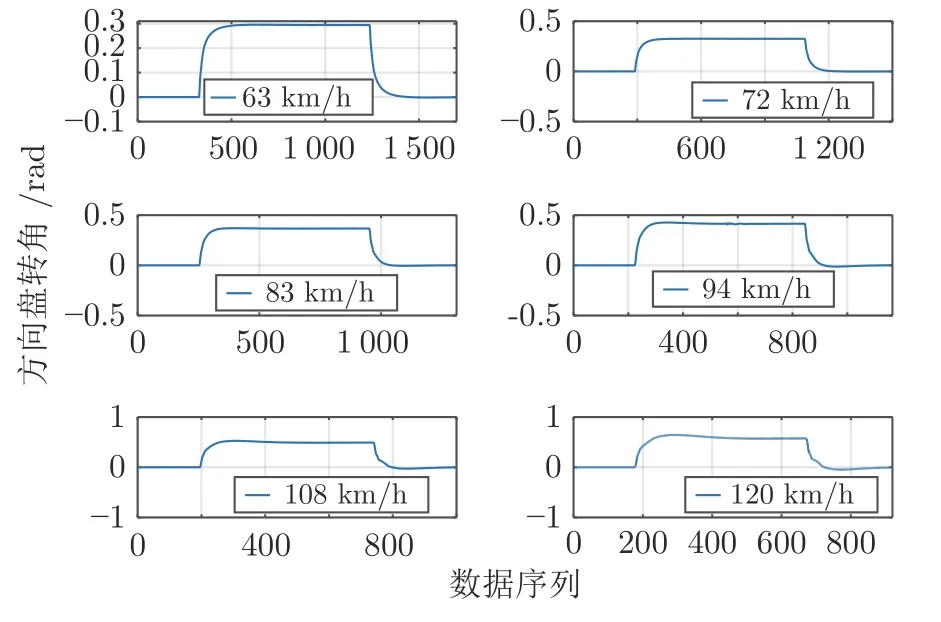
图24 不同车速下方向盘的输出转向角Fig.24 Output steering angle of steering wheel at different speeds
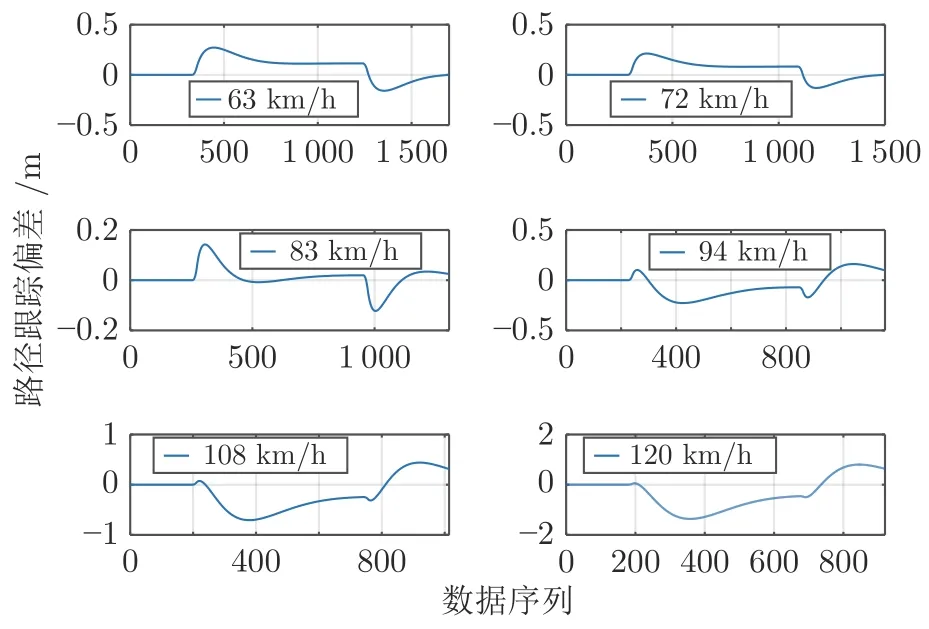
图25 不同车速下车辆的路径跟踪偏差Fig.25 Vehicle path tracking deviation at different speeds
为了更加直观地分析车辆的路径跟踪情况,将不同车速下路径跟踪偏差的相关指标统计如表7所示,可以看出,当车速低于 94 km/h 时,车辆的路径跟踪的峰值偏差能够保持在 0.23 m 以内,说明该控制器能够有效保证车辆的路径跟踪性能.

表7 不同车速下的车辆路径跟踪偏差指标对比Table 7 Comparison of route tracking deviation index at different vehicle speeds
3.2.2 人机共驾在线测试
在第3.2.1 节中对控制器单独驾驶进行了验证,可见控制器在单独驾驶时能够有效完成路径跟踪任务.接下来进行半实物的台架实验,分别采用罗技的实物驾驶单元、CarMaker 软件、MATLAB 完成对双环人机协同驾驶的实验,进而讨论人机协同驾驶下的车辆的道路跟踪特性以及安全特性.另外还需要讨论控制器加入人机协同控制是否能够提高车辆的转向精度、优化驾驶员的转向操作、降低驾驶员的驾驶负担.
基于以上目标,我们分别采集驾驶员A、驾驶员B、驾驶员C在人机协同控制中的转向实验数据.人机共驾测试示意图如图26 所示,车速设定为65 km/h,分别让驾驶员A进行正常的转向操作,驾驶员B进行过度转向操作,驾驶员C进行欠转向操作.然后分析不同驾驶员在不同转向模式下的方向盘转向角的变化以及车辆道路跟踪的偏差情况.

图26 人机共驾测试示意图Fig.26 Man-machine co-driving test
如图27 所示,当驾驶员A在正常转向的情况下,驾驶员此时的转向操作较为精准,当经过权重后的输出转向角与驾驶员产生的转向角较为接近,可以得到,如图28 所示,如果驾驶员在进行正常转向的情况下且保证车辆的路径跟踪误差在允许的范围内,共享系统会增加驾驶员的驾驶权重.从而达到辅助驾驶员进行转向操作的功能.如图29 所示,驾驶员A在正常转向的情况下,车辆的路径跟踪偏差维持在较小的水平,完全能够满足车辆通过的安全性.

图27 驾驶员A 正常转向下驾驶员转角与权重后的输出转向角对比Fig.27 Contrast of driver's angle with output steering angle after weight under driver A's normal steering
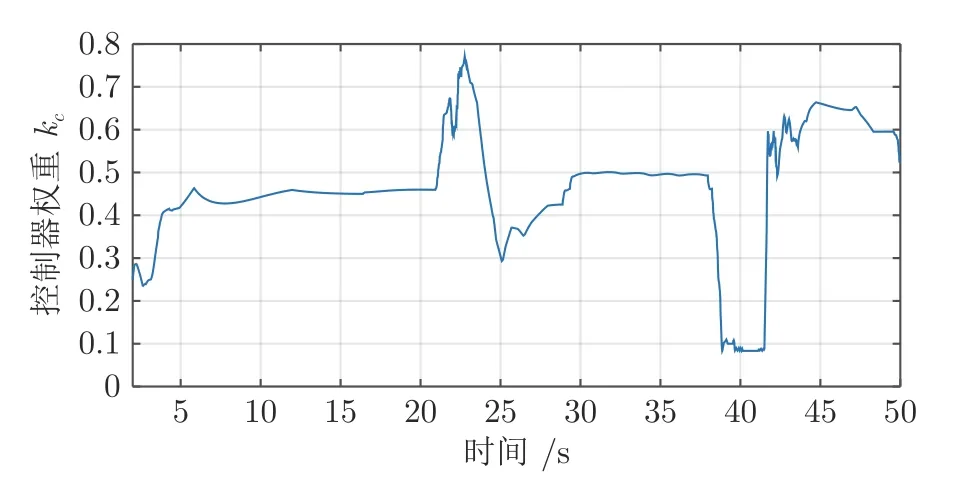
图28 驾驶员A 正常转向下控制器权重的变化Fig.28 Variation of controller weight under driver A's normal steering
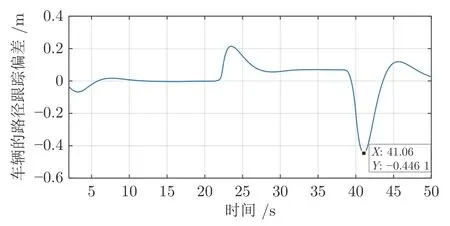
图29 驾驶员A 正常转向下车辆的路径跟踪偏差Fig.29 Vehicle path tracking deviation under driver A's normal steering
当驾驶员B在过度转向的情况下,如图30 所示,驾驶员输出的转向角明显高于正常的转向角水平,但是,驾驶员的转向角经过权重后输出的转向角能够保持在正常值的水平.如图31 可见,当驾驶员进行过度转向操作的情况下,控制器的控制权重会增加,对应的降低了驾驶员的控制权重,从而达到纠正驾驶员的功能.如图32 所示,当驾驶员B在过度转向的情况下,共享系统仍旧能够将车辆的跟踪路径偏差维持在安全的范围内.虽然驾驶员B比驾驶员A产生的转向角误差较大,但是此时控制器的控制权重提升,以此保证车辆的通过性.
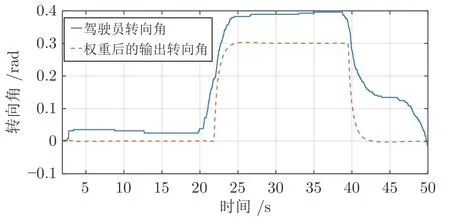
图30 驾驶员B 过度转向下驾驶员转角与权重后的输出转向角对比Fig.30 Contrast of driver's angle under driver B oversteering with output steering angle after weighting

图31 驾驶员B 过度转向下控制器权重的变化Fig.31 Variation of controller weight under driver B's oversteering
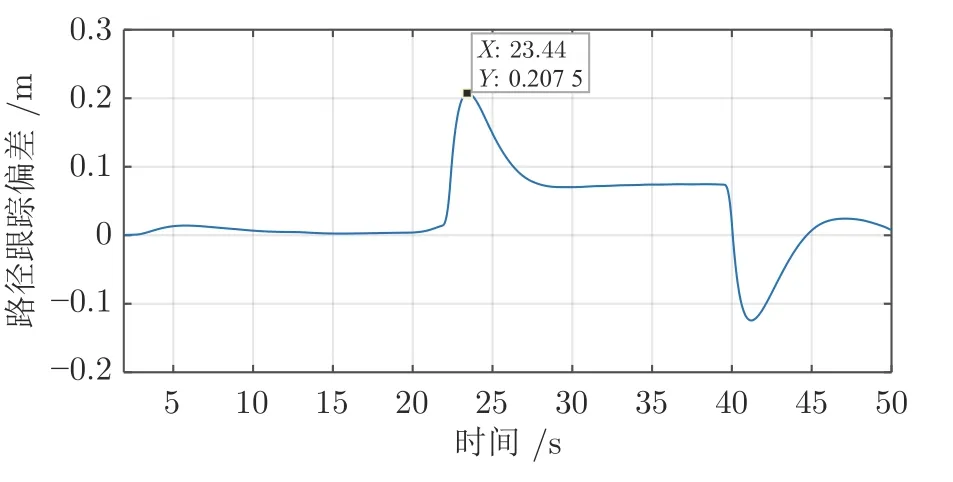
图32 驾驶员B 过度转向下车辆的路径跟踪偏差Fig.32 Vehicle path tracking deviation under driver B's oversteering
当驾驶员C在转向不足的情况下,如图33 所示,驾驶员输出的转向角明显低于正常的转向角水平,但是,驾驶员的转向角经过权重后输出的转向角依旧能够将保持在正常值的水平.此时同样是增加了控制器的控制权重,从而补偿驾驶员的转向操作.如图34 所示,当驾驶员C在转向不足的情况下,共享系统能将车辆的跟踪偏差维持在安全值的范围内.可见,无论驾驶员是在过度转向还是在转向不足的情况下,共享系统都能保证车辆的路径跟踪要求.

图33 驾驶员C 转向不足时驾驶员转角与权重后的输出转向角对比Fig.33 Contrast the driver's angle with weighted output steering angle when C is insufficient turning
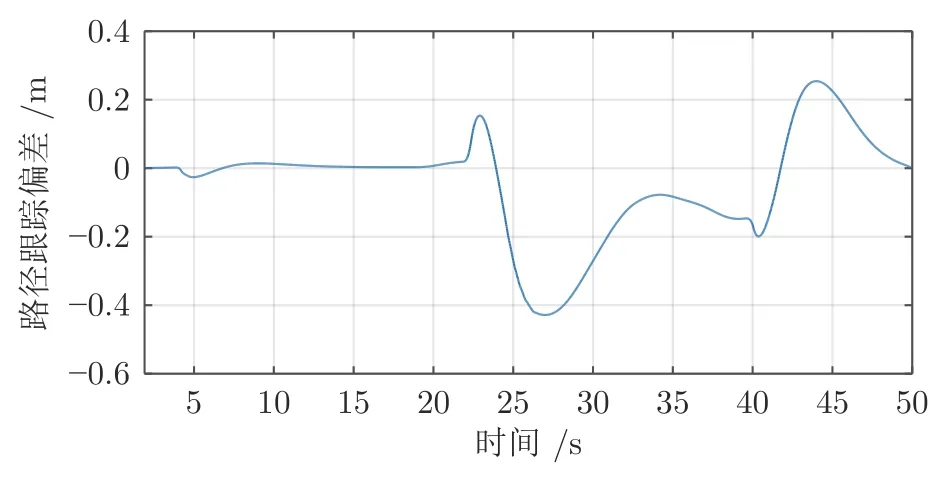
图34 驾驶员C 转向不足时车辆的路径跟踪偏差Fig.34 Vehicle path tracking deviation when driver C steering is insufficient
最后,本文将讨论共享驾驶相较驾驶员C单独驾驶的差异.如图35 所示,共享驾驶的情况下,驾驶员产生的转向角小于单独驾驶时驾驶员产生的转向角.如图36 所示,共享驾驶的情况下,驾驶员产生的输出力矩小于单独驾驶时驾驶员产生的力矩.为了进一步比较单独驾驶与共享驾驶的差异,将相关数据制作成统计表如图37 所示,给出了驾驶员C单独驾驶和共享驾驶下的平均力矩、平均功率和总功率的统计直方图,可以看出共享驾驶情况下比单独驾驶的3 项指标都要小.说明共享驾驶能够有效减轻驾驶员的驾驶负担.图38 和图39 给出了驾驶员单独驾驶的路径跟踪偏差和共享驾驶的路径跟踪偏差,其中最大偏差分别是 0.78 m 和 0.16 m,可见共享系统能够极大地提升路径跟踪的精度.

图35 驾驶员C 单独驾驶与共享驾驶下转向角对比Fig.35 Contrast of insufficient steering angle between driver C driving alone and shared driving
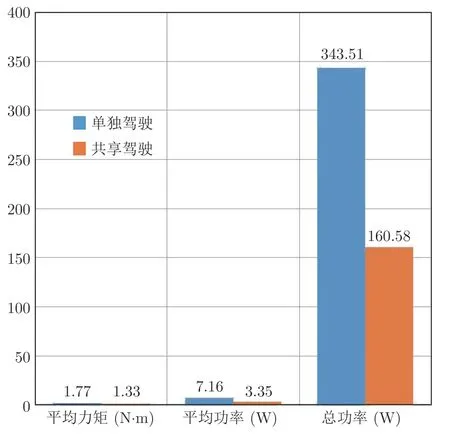
图37 驾驶员C 单独驾驶与共享驾驶下驾驶员各项指标对比Fig.37 Contrast of driver's index between driver C driving alone and shared driving

图38 驾驶员C 单独驾驶的路径跟踪偏差Fig.38 Vehicle path tracking deviation when driver C driving alone

图39 驾驶员C 共享驾驶下的路径跟踪偏差Fig.39 Vehicle path tracking deviation under shared driving for driver C
由此可见,在驾驶员正常驾驶、过度转向、转向不足的不同驾驶模式下,共享系统都能提升驾驶路径的精度、减小驾驶员的驾驶负荷.
为了进一步对比分析,表8 给出了4 种驾驶行为下的路径跟踪偏差的峰值误差、和方差、均方差、均方根数据.可见,共享驾驶能够有效减小车辆的道路跟踪偏差,提升驾驶过程中的安全性,另外减轻了驾驶员的驾驶负担.
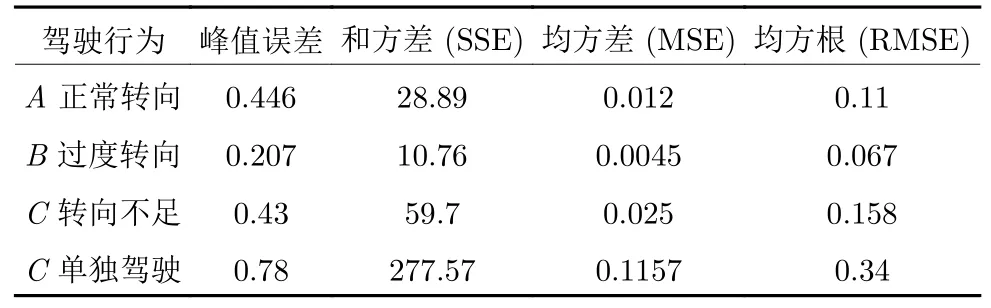
表8 不同驾驶模式下车辆的路径跟踪偏差指标对比Table 8 Comparison of vehicle path tracking deviation index under different driving mode
4 结束语
本文首先建立驾驶员转向模型,然后通过遗传算法辨识模型参数并分析其与车速和道路曲率之间的函数关系,最后在线验证了共享控制系统的相关性能.
结果表明该系统不仅能够更好地辅助驾驶员实现转向操控行为,提升车辆的轨迹跟踪精度和安全性,还能够极大地减轻驾驶员负荷.但是仍存在一定的缺陷,比如,当车辆在高速状态时,模型参数的辨识误差较大.因此,需要对模型的结构和参数进行进一步的优化,同时也可以对遗传算法进行优化.另外,本文的验证与实验中只采用了简单的弯道路况,今后可以深入研究驾驶员转向模型在复杂工况下的特点.在仿真实验的环节,考虑城市路况,利用低速数据进行分析,同时讨论路面附着系数的影响;另外需要考虑一些环境干扰较大的因素,例如风阻,道路颠簸等;同时可以设计鬼探头极限工况;此外,共享控制系统也需要不断优化,例如加入驾驶员状态监测与意图识别模块来提高共享系统的性能.速度变化的模型参数辨识过程更符合实际情况,也值得进一步研究.
