基于WOA-BP算法的海底管道腐蚀速率预测
2022-08-01肖荣鸽靳帅帅
肖荣鸽, 靳帅帅
基于WOA-BP算法的海底管道腐蚀速率预测
肖荣鸽, 靳帅帅
(西安石油大学 石油工程学院 陕西省油气田特种增产技术重点实验室, 陕西 西安 710065)
管道腐蚀速率的影响因素众多, 构成了异常复杂的腐蚀体系, 很难对其进行准确预测。针对单一BP模型初始权值和阈值的选取不当容易陷入局部最优等问题, 引入WOA算法优化BP神经网络对海底管道腐蚀速率进行预测, 并与GA和PSO算法优化BP预测模型进行对比, 验证WOA-BP模型的预测效果和可行性。结果表明: WOA-BP模型的平均绝对百分误差和均方根误差分别为3.689% 和0.1537, 远低于单一BP、PSO-BP、GA-BP模型, 具有较高的预测精度和稳定性, 可以为海底管道内腐蚀防护和油气管道流动保障提供决策支持。
腐蚀速率; WOA算法; BP模型; GA算法; PSO算法
石油与天然气在我国能源战略中占据重要的地位, 关乎国家发展命脉。管道运输作为油气输送最为普遍的方式之一, 已发展成为我国的第五大运输行业。但在管道运行时, 受环境和管输介质影响, 不可避免的会出现管道腐蚀, 进而发生各种安全事故。据统计, 除人为破坏外, 管道的失效形式以腐蚀失效为主, 腐蚀是影响管道可靠运行的主要影响因素, 一般用腐蚀速率作为管道腐蚀的评价指标[1]。影响管道腐蚀的因素有很多, 如管输介质的温度、流速、pH、溶解氧和CO2含量等, 构成了异常复杂的腐蚀体系, 并且很难找到腐蚀速率与各影响变量之间的函数关系[2]。因此, 在管道的腐蚀速率预测方面, 经典的预测方法变得不再适用。
随着计算机科学的兴起, 智能算法逐渐应用于管道腐蚀速率预测方面。范峥等[3]基于多相流动态实验, 利用小波神经网络建立油气集输管道的腐蚀速率预测模型; 章玉婷等[4]使用单一的BP神经网络(BP neural network, BPNN)对管道腐蚀速率进行分析预测, 由于未经优化的BP易陷入局部最优, 因此预测值相对真实数据误差较大。为了解决单一神经网络算法精度不高的问题, 研究者提出将优化算法与神经网络结合用于腐蚀速率预测。周慧等[5]提出了将灰色模型、多项式回归模型与人工神经网络组合的用于预测输气管道腐蚀速率的组合模型, 提高了预测精度和增强了预测模型的自适应性; 万里平等[6]提出了基于GA-BP的输油管道内腐蚀速率预测模型, 运用遗传算法优化BP神经网络的权值和阈值, 有效避免了单一BP容易陷入局部最优的缺陷; 凌晓等[7]为了解决初始模型参数对BP神经网络预测精度的影响, 提出了粒子群算法优化BP神经网络的腐蚀速率预测模型, 提高了模型的预测精度和稳定性。
鲸鱼算法(whale optimization algorithm, WOA)是Mirjalili等[8]受鲸鱼独特的气泡网捕食机制启发, 提出的一类群体智能算法, 该算法具有操作简单, 调整的参数少以及寻优能力强等优点。采用WOA算法优化BP神经网络, 不仅可以有效避免单一BP容易陷入局部最优和预测不稳定等问题的发生, 还可以提升自身搜索到全局最优的能力[9]。因此, 本文引入WOA算法优化BP神经网络进行海底管道腐蚀速率仿真, 并与遗传算法(genetic algorithms, GA)和粒子群算法(particle swarm optimization, PSO)优化BP预测模型进行对比, 验证WOA-BP模型的预测效果和可行性。
1 BP神经网络及各优化算法原理
1.1 BP神经网络
BP神经网络[10-11]是一类多层的前馈神经网络, 其原理是: 通过大量的网络训练, 利用误差的反向传播, 不断调整网络的权值和阈值, 减小误差, 实现复杂变量的非线性映射和数据联想功能。BP神经网络一般采用三层网络拓扑结构即输入层、隐含层和输出层, 如图1所示。输入层和输出层的节点数由输入数据和输出数据的类型确定, 隐含层的节点数由式(1)确定。当样本数据输入之后, 神经元被激活, 沿输入层→隐含层→输出层路径传播计算, 而输出误差沿相反路径反馈到输入层, 此时变量正传播与误差逆传播交替进行。如果预测不合理, 通过对隐含层的权值和阈值进行修正, 不断迭代, 直至预测结果满足要求。
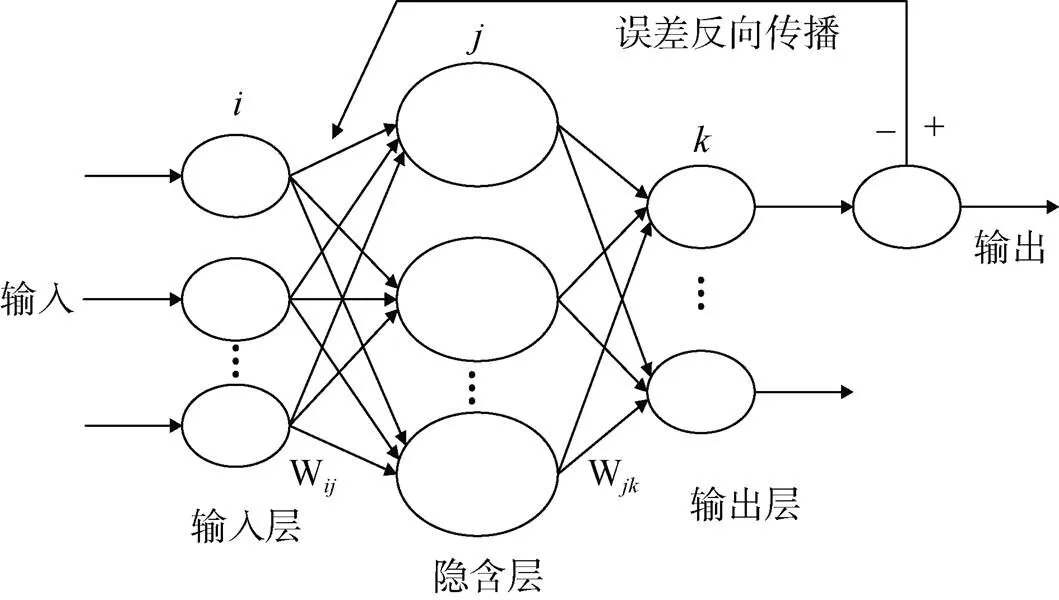
图1 BP神经网络结构
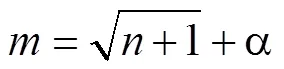
式中,为隐含层节点数,为输入层节点数,为输出层节点数, α为1~10之间的常数。
1.2 WOA算法
WOA算法通过模拟座头鲸的觅食行为, 构建出随机搜索捕食、包围捕食和气泡网捕食等理论模型, 以实现对目标问题的优化求解, 具有稳定性强、调节参数少等优点[12-13]。
该算法提出的主要数学方程如下:
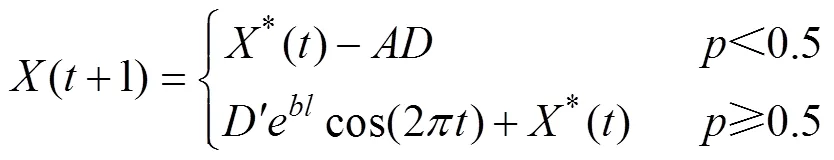
其中,′=|*()–()|,=|*()–()|,=2–,=2,是[0, 1]之间的一个随机数;()和*()分别表示当前鲸鱼位置和每次迭代的最优解,′表示第条鲸鱼的最佳捕食位置,是定义螺旋形状的常数,为[–1, 1]的随机数,表示迭代次数,是在迭代过程中线性地从2减小到0的常数。
方程(2)的第一部分模拟了包围机制, 而第二部分模拟了气泡网捕猎技术。变量以相等的概率在这2个部分之间切换。
在鲸鱼算法中, 参与捕猎行为的每头鲸鱼都代表一个可行解。在每一代的游动中, 鲸鱼们会随机选择3种觅食行为向着最优位置的猎物捕猎或者通过包围收缩进行位置的更新, 不断逼近目标猎物, 直至找到最优解[14]。
1.3 GA算法
遗传算法是Holland[15]受达尔文进化理论启发于1962年提出的随机搜索优化算法。它把自然界中的“物竞天择, 适者生存”的生物进化原理引入算法中, 通过设置的适应度函数对种群采取选择、交叉和变异操作, 进行个体筛选, 淘汰适应度差的个体, 保留适应度好的个体, 实现种群的信息更新。这样反复循环, 直到满足终止条件。
遗传算法具有智能性和并行性两种优点。该算法在演化过程中将获得的信息自行组织搜索, 将适应值大的个体保留下来, 是具有“潜在学习能力”的自适应技术, 容易直接移植到实际问题中。遗传算法在本质上是并行的, 包括内在并行性和内含并行性, 非常适于求解复杂问题, 以及搜索复杂的解空间, 能够以较少的计算获得较大的收益[16-17]。
1.4 PSO算法
粒子群优化算法是Kennedy和Eberhart[18]受鸟群捕食行为启发提出的一类随机搜索算法, 通过模拟鸟群的迁徙和群聚行为, 在计算机上建立群体模型仿真, 实现对目标问题的优化求解[19]。
粒子群算法的基本思想是: 将鸟群中的每个个体当做优化问题的潜在解即粒子, 每个粒子通过跟踪个体极值和全局极值来更新自己, 然后通过适应度函数决定下一步的飞翔方向和距离, 不断迭代直至找到最优解。该算法具有调节参数少、简单易实现等优点, 被广泛应用于复杂问题寻优等应用领域[20-21]。
2 管道腐蚀速率预测模型构建
2.1 模型搭建
结合第一节建立的理论模型, 分别使用PSO、GA、WOA算法依次对BP神经网络模型的权值和阈值进行优化, 构建海底管道的腐蚀速率预测模型即PSO-BP、GA-BP、WOA-BP, 流程图如图2所示。

图2 各预测模型流程图
2.2 模型评价指标
为综合评价腐蚀速率预测模型的预测精度, 选取平均绝对百分误差(MAPE)、均方根误差(RMSE)[22]作为模型评价指标:
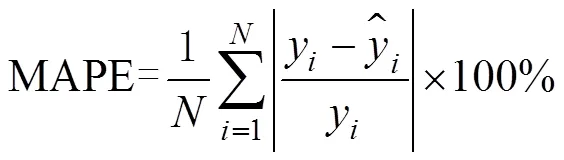
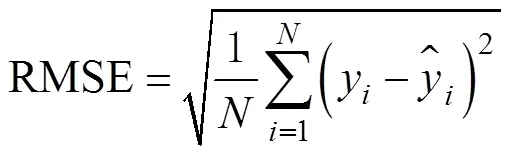
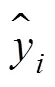
3 实例计算
3.1 样本数据的收集与处理
本文选用文献[23]的50组海底管道腐蚀数据作为样本数据, 因篇幅有限, 文内仅展示10组, 如表1所示。随机选取40组数据作为训练样本, 利用剩余的10组进行精度验证。
3.2 灰色关联分析
每个影响因素对管道腐蚀的影响程度不同, 若将影响小的因素作为预测模型的输入, 则会影响预测模型的准确性和计算复杂度, 因此对各影响因素进行影响程度分析具有重要意义。
灰色理论[24]是邓聚龙于1982年提出的用于判别不同因素间关联程度的一种方法。该方法无需要求各影响因素之间具有明显的函数关系, 只需要通过数学变换就能进行影响因素分析。本文通过灰色理论分析, 建立各影响因素与腐蚀速率之间的关联度。关联度越大, 影响程度越大。通过灰色关联分析, 得到各影响因素的关联度, 如表2所示。
由表2可知, 各影响因素对腐蚀速率的影响程度从大到小依次为: 温度>HCO3–>CO2分压>系统压力> CO2浓度>含水率>介质流速>pH>Cl–浓度, 均在0.6以上。结果表明各影响因素与腐蚀速率的相关性都很大, 可以作为预测模型的输入参数。
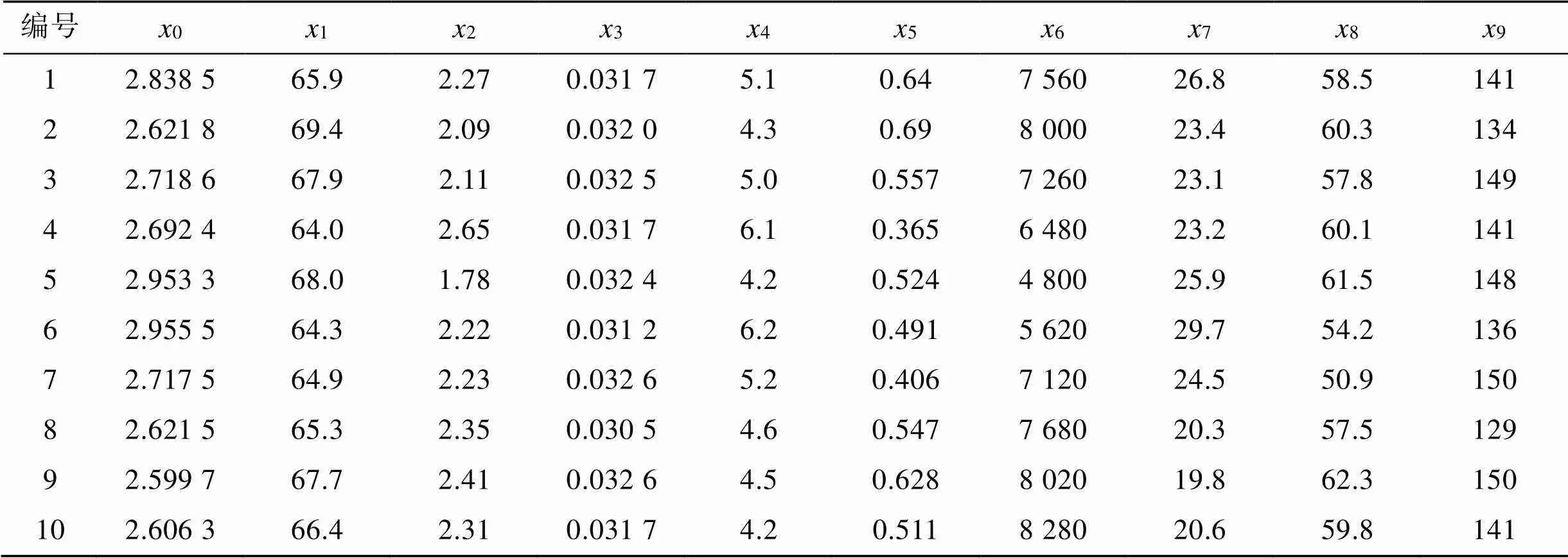
表1 部分海底管道腐蚀速率数据[23]
注:0为腐蚀速率(mm·a–1),1为温度(℃),2为系统压力(MPa),3为CO2分压(MPa),4为pH值,5为介质流速(m·s–1),6为Cl–浓度(mg·L–1),7为CO2浓度(mg·L–1),8为含水率(%),9为HCO3–浓度(mg·L–1)。

表2 各影响因素灰色关联分析
3.3 模型参数设置
3.3.1 BP神经网络设置
设定BP神经网络学习的训练次数为1 000, 学习速率为0.01, 训练目标最小误差为0.000 01。BP神经网络采用3层网络结构, 由于管道腐蚀速率的影响变量为9, 目标变量为腐蚀速率, 所以输入层节点数取9, 输出层节点数取1。一般来说, 隐含层的节点数不是唯一的, 而是在一个区间范围内。根据经验公式(1)确定隐含层节点数区间, 通过试值的方式确立最优节点数。经计算,的取值为4~13, 代入模型进行计算可得图3。
由图3可知, 最佳的隐含层节点数为4, 相应的均方误差为0.175 6。因此, 本模型隐含层节点数取4。
3.3.2 模型初始化设置
通过以上分析, 设置PSO-BP、GA-BP、WOA-BP模型的网络拓扑结构为9-4-1。各优化算法的初始参数设定如表3、表4、表5所示。
WOA除了设置表5中参数, 还需要对位置向量和领导者得分进行初始化操作。
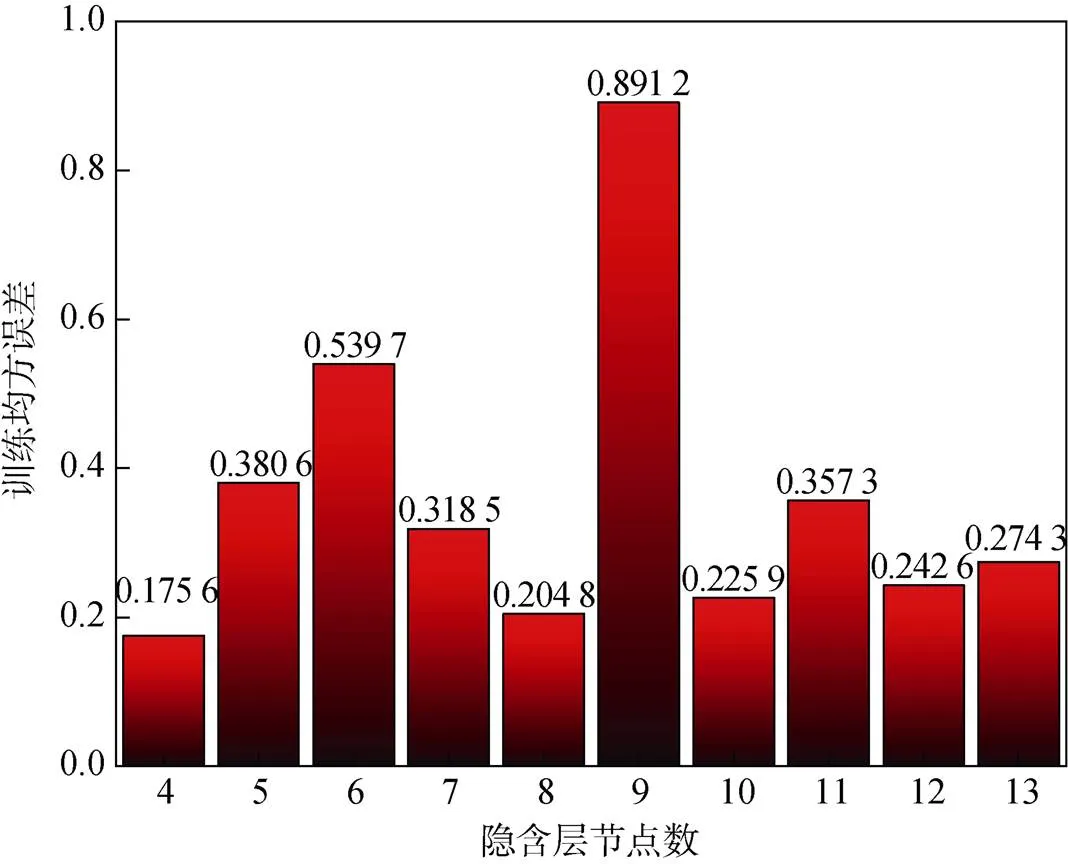
图3 m取不同值的训练均方误差

表3 GA参数设置

表4 PSO参数设置
3.4 预测结果与误差检验
各模型进行训练后的预测结果如表6、图4、图5所示。由图4可知, WOA-BP腐蚀速率预测模型的预测值与实验值最接近, 预测效果最好, 相较于单一BP模型, 预测精度有了较大提升, 并且优于PSO-BP与GA-BP预测模型。
由表6、图5可知, 单一BP模型的预测效果最差, 最大相对误差和最小相对误差分别为20.29%和0.14%, 预测结果极其不稳定。WOA-BP模型的预测效果最好, 其相对误差基本稳定在3%以内, 误差曲线也最为平缓。对各模型的平均相对误差进行计算, 其中WOA-BP模型的平均相对误差最小, 为3.689%; PSO-BP和GA-BP模型的平均相对误差分别为5.868%和6.14%, 分别位于第2位和第3位; 单一BP模型的平均相对误差最大, 为8.142%。
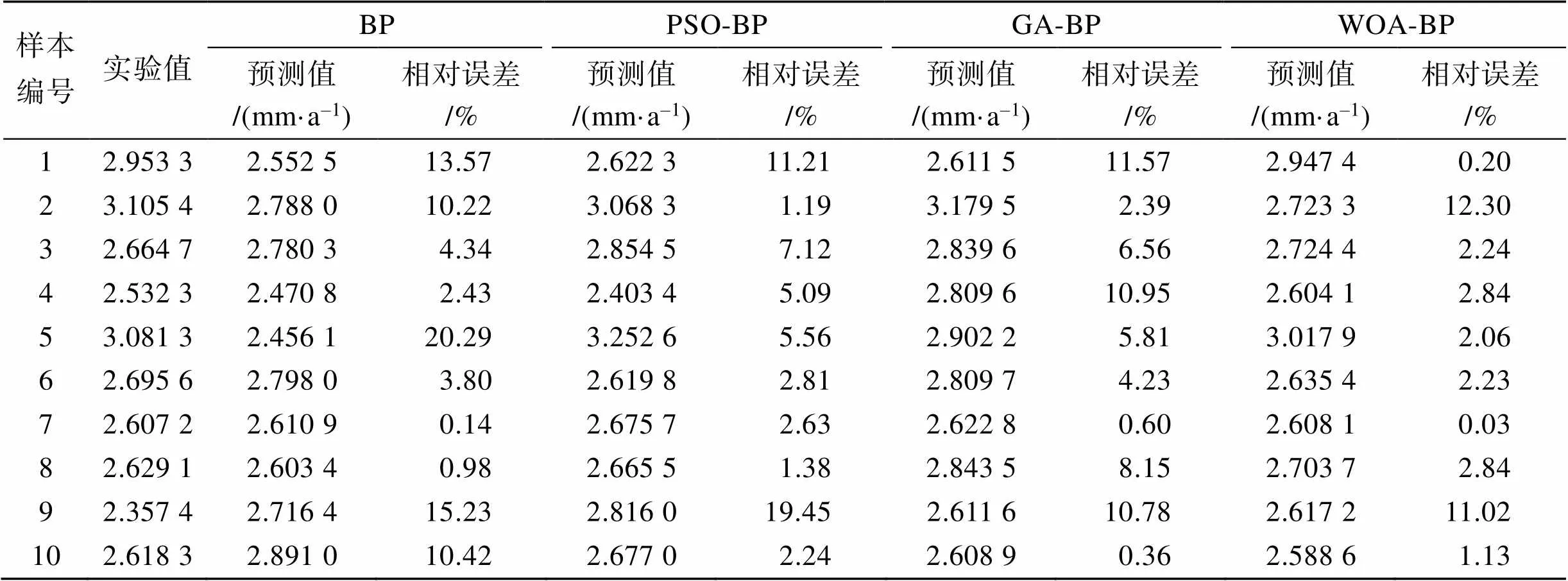
表6 模型预测误差统计表
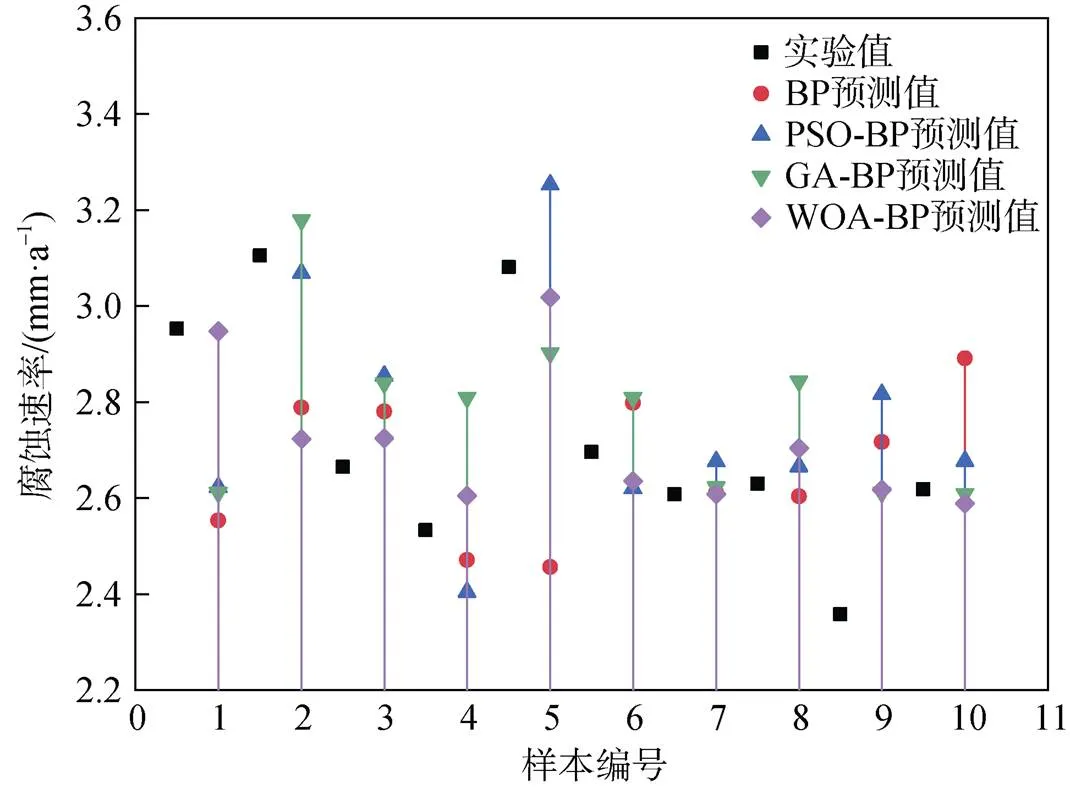
图4 各模型预测结果对比图
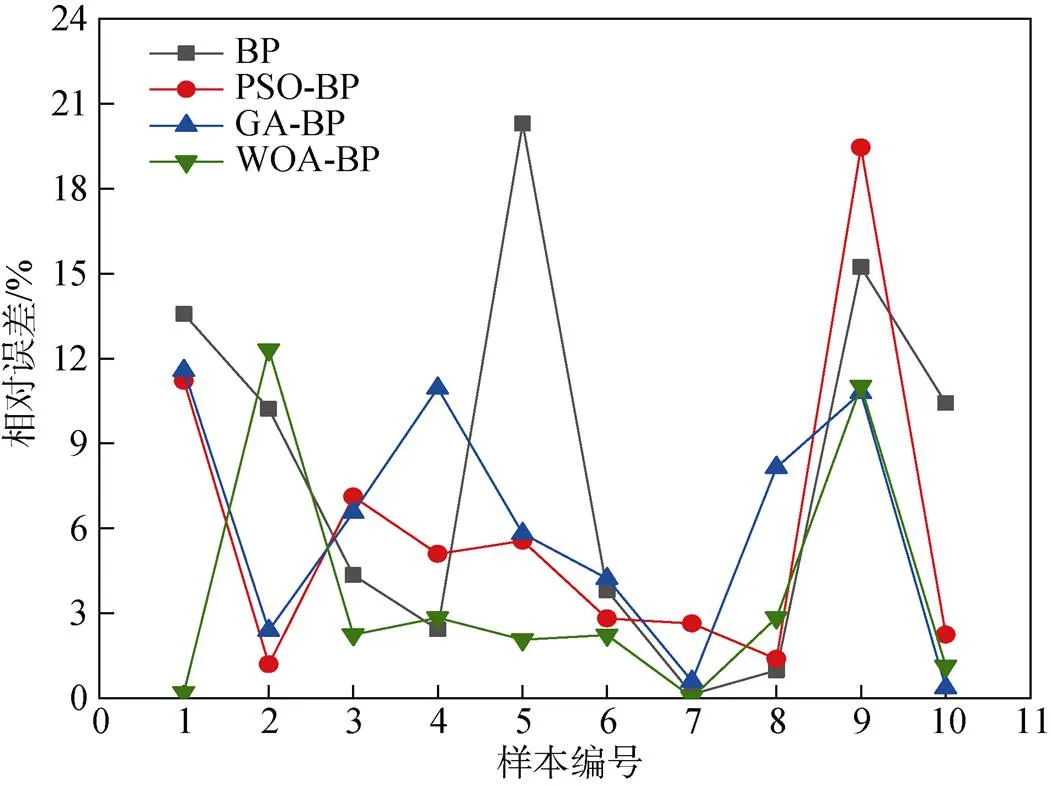
图5 各模型相对误差对比
利用式(3)和式(4)计算各模型的MAPE和RMSE, 对模型精度进行更深层次的验证, 计算结果如图6所示。
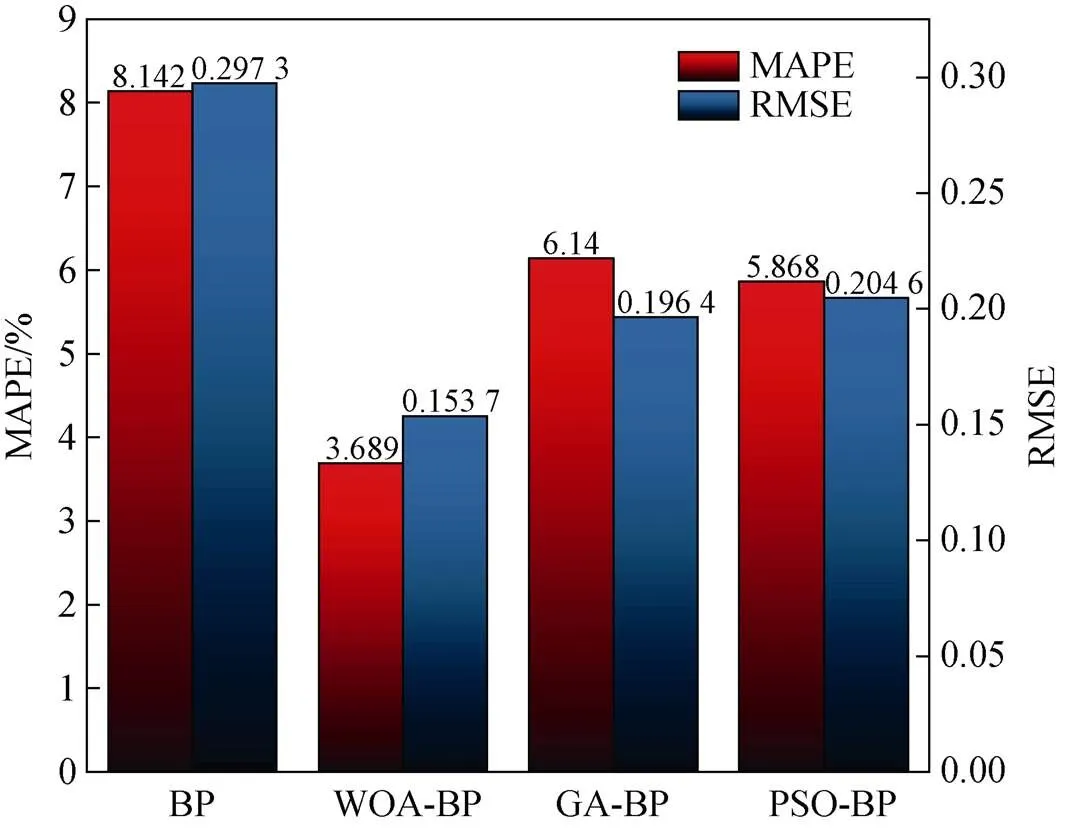
图6 各模型MAPE与RMSE
由图6可知, WOA-BP模型的平均绝对百分误差和均方根误差分别为3.689%和0.153 7, 远低于单一BP模型、PSO-BP模型和GA-BP模型, 预测结果理想。
以上结果表明, 4种模型中预测精度最高、预测结果最稳定的是WOA-BP模型, 该模型能很好地应用于海底管道腐蚀速率预测。
3.5 WOA-BP模型的适用范围
由于WOA-BP模型建立时选取的数据遵循相互独立、数据范围广、随机选取的原则, 为后面预测提供精准的训练数据。因此, 本模型适用于任意环境下的管道腐蚀速率预测。
4 结论
1) 基于灰色理论, 对影响海底管道腐蚀速率的9个影响变量进行灰色关联分析, 得到各影响变量对腐蚀速率的关联度从大到小依次为: 温度>HCO3–> CO2分压>系统压力>CO2浓度>含水率>介质流速> pH>Cl–浓度。结果表明: 各影响因素与腐蚀速率的相关性都很大, 可以作为预测模型的输入参数。
2) 分别采用单一BP模型、PSO-BP模型、GA-BP模型以及WOA-BP模型对海底管道腐蚀速率进行训练和仿真。WOA-BP模型的平均绝对百分误差和均方根误差分别为3.689%和0.153 7, 远低于单一BP、PSO-BP、GA-BP模型, 验证了WOA-BP模型的预测精度和稳定性。说明WOA-BP模型可为海底管道内腐蚀防护和油气管道流动保障提供决策支持。
3) 由于影响管道腐蚀的因素众多且相互作用, 工程上很难得到完整的实验数据, 后续研究可在数据中添加随机变量进行深入研究。
[1] 崔铭伟. 多相流海管CO2内腐蚀及剩余强度研究[D]. 青岛: 中国石油大学(华东), 2014.
Cui Mingwei. Study on CO2internal corrosion and residual strength of multiphase offshore pipeline[D]. Qingdao: China University of Petroleum, 2014.
[2] 喻西崇, 赵金洲, 邬亚玲, 等. 利用灰色理论预测注水管道腐蚀速率的变化趋势[J]. 腐蚀与防护, 2003, 24(2): 51-54, 69.
Yu Xichong, Zhao Jinzhou, Wu Yaling et al. Using gray model to predict corrosion rate variation with time in injecting pipeline[J]. Corrosion & Protection, 2003, 24(2): 51-54, 69.
[3] 范峥, 付文耀, 赵笑男, 等. 基于小波神经网络预测多相动态管道腐蚀速率[J]. 化工进展, 2018, 37(8): 2904-2911.
Fan Zheng, Fu Wenyao, Zhao Xiaonan, et al. Prediction of tubular corrosion rate under multiphase dynamics condition based on wavelet neural network[J]. Chemical Industry and Engineering Progress, 2018, 37(8): 2904-2911.
[4] 章玉婷, 杨剑锋. 基于BP神经网络的管道腐蚀速率预测[J]. 全面腐蚀控制, 2013, 27(9): 67-71.
Zhang Yuting, Yang Jianfeng. Corrosion rate prediction of based on artificial neural network[J]. Total Corrosion Control, 2013, 27(9): 67-71.
[5] 周慧, 王晓光, 张有君. 输气管道腐蚀速率的BP神经网络组合预测方法[J]. 腐蚀科学与防护技术, 2010, 22(3): 162-165.
Zhou Hui, Wang Xiaoguang, Zhang Youjun. BP neural networks combinatorial forecasting method for gas pipeline’s corrosion rate[J]. Corrosion Science and Protection Technology, 2010, 22(3): 162-165.
[6] 万里平, 徐友红, 冯兆阳, 等. 基于遗传算法优化BP神经网络预测CO2/H2S环境中套管钢的腐蚀速率[J]. 腐蚀与防护, 2017, 38(9): 727-731, 736.
Wan Liping, Xu Youhong, Feng Zhaoyang, et al. Application of genetic algorithms BP neural networks to predicting corrosion rate of carbon steel in CO2/H2S environment[J]. Corrosion & Protection, 2017, 38(9): 727-731, 736.
[7] 凌晓, 徐鲁帅, 梁瑞, 等. 基于改进PSO-BPNN的输油管道内腐蚀速率研究[J]. 中国安全生产科学技术, 2019, 15(10): 63-68.
Ling Xiao, Xu Lushuai, Liang Rui, et al. Study on internal corrosion rate of oil pipeline based on improved PSO-BPNN[J]. Journal of Safety Science and Technology, 2019, 15(10): 63-68.
[8] Mirjalili s, Lewis A, et al. The whale optimization algorithm[J]. Advances in Engineering Software, 2016, 95: 51-67.
[9] 王镱嬴. 基于改进鲸鱼算法的神经网络预测模型的研究[D]. 鞍山: 辽宁科技大学, 2020.
Wang Yiying. Research of neural network orediction model based on modified whale optimization algorithm[D]. Anshan: University of Science and Technology Liaoning, 2020.
[10] 李海涛, 袁森. 基于遗传算法和BP神经网络的海洋工程材料腐蚀预测研究[J]. 海洋科学, 2020, 44(10): 33-38.
Li Haitao, Yuan Sen. Corrosion prediction of marine engineering materials based on genetic algorithm and BP neural network[J]. Marine Sciences, 2020, 44(10): 33-38.
[11] 凌晓, 徐鲁帅, 余建平, 等. 基于改进的BP神经网络的输油管道内腐蚀速率预测[J]. 传感器与微系统, 2021, 40(2): 124-127.
Ling Xiao, Xu Lushuai, Yu Jianping, et al. Prediction of corrosion rate in oil pipeline based on improved BP neural network[J]. Transducer and Microsystem Technologies, 2021, 40(2): 124-127.
[12] 骆正山, 秦越, 张新生, 等. 基于LASSO-WOA- LSSVM的海洋管线外腐蚀速率预测[J]. 表面技术, 2021, 50(5): 245-252.
Luo Zhengshan, Qin Yue, Zhang Xinsheng, et al. Prediction of external corrosion rate of marine pipelines based on LASSO-WOA-LSSVM[J]. Surface Technology, 2021, 50(5): 245-252.
[13] 巩世兵, 沈海斌. 仿生策略优化的鲸鱼算法研究[J]. 传感器与微系统, 2017, 36(12): 10-12.
Gong Shibing, Shen Haibin. Study of whale algorithm for biomimetic strategy optimization[J]. Transducer and Microsystem Technologies, 2017, 36(12): 10-12.
[14] 李志鹏, 陈堂贤. 基于变分模态分解和改进鲸鱼算法优化的神经网络风速预测模型[J]. 电器与能效管理技术, 2019(11): 24-31.
Li Zhipeng, Chen Tangxian. Optimized fuzzy neural network wind speed prediction model based on VMD and improved whale algorithm[J]. Electrical & Energy Management Technology, 2019(11): 24-31.
[15] Holland J H. Genetic algorithms[J]. Scientific american, 1992, 267(1): 66-73.
[16] 向乃瑞, 闫海, 王炜, 等. GA-BP神经网络预测金属腐蚀速率[J]. 电力学报, 2018, 33(1): 48-54.
Xiang Nairui, Yan Hai, Wang Wei, et al. Prediction of metal corrosion rate based on GA-BP neural network[J]. Journal of Electric Power, 2018, 33(1): 48-54.
[17] 商杰, 朱战立. 基于遗传算法的神经网络在预测油管钢腐蚀速率中的应用[J]. 腐蚀科学与防护技术, 2007, 19(3): 225-228.
Shang Jie, Zhu Zhanli. Application of genetic algorithms neural networks in prediction corrosion rate of carbon steel[J]. Corrosion Science and Protection Technology, 2007, 19(3): 225-228.
[18] Kennedy J, Eberhart R. Particle swarm optimization[C]// Icnn95-international Conference on Neural Networks. IEEE, 2002.
[19] 张新生, 张玥. 基于Lasso-PSO-BP神经网络的腐蚀管道失效压力的预测[J]. 材料保护, 2020, 53(4): 46- 52.
Zhang Xinsheng, Zhang Yue. Prediction of failure pressure of corroded pipeline based on Lasso-PSO-BP neural network[J]. Materials Protection, 2020, 53(4): 46-52.
[20] 黄宝洲, 杨俊华, 卢思灵, 等. 基于改进粒子群优化神经网络算法的波浪捕获功率预测[J]. 太阳能学报, 2021, 42(2): 302-308.
Huang Baozhou, Yang Junhua, Lu Siling, et al. Wave capture power forecasting based on improved particle swarm optimization neural network algorithm[J]. Acta Energiae Solaris Sinica, 2021, 42(2): 302-308.
[21] 张玥. 基于有限元和PSO-BP的多点腐蚀缺陷管道剩余强度研究[D]. 西安: 西安建筑科技大学, 2020.
Zhang Yue. Residual strength of multi-point corroded pipeline based on finite element and PSO-BP[D]. Xi’an: Xi’an University of Architecture and Technology, 2020.
[22] 纪广月. 基于因子分析和WOA-Elman的肇庆API预测研究[J]. 数学的实践与认识, 2021, 51(11): 265-276.
Ji Guangyue. Prediction of Zhaoqing API based on factor analysis and WOA Elman neural network[J]. Mathematics in Practice and Theory, 2021, 51(11): 265- 276.
[23] 宋莹莹. 在役海底油气管道内腐蚀速率预测研究[D]. 西安: 西安建筑科技大学, 2020.
Song Yingying. Research for internal corrosion rate prediction of submarine oil and gas pipelines in service[D]. Xi’an: Xi’an University of Architecture and Technology, 2020.
[24] 邓聚龙. 灰色系统论文集[M]. 武汉: 华中理工大学出版社, 1989.
Deng Julong. Collection of grey system essays[M]. Wuhan: Huazhong University of Science and Technology Press, 1989.
Prediction of the submarine pipeline corrosion rate based on the whale optimization algorithm and back propagation (WOA-BP) algorithm
XIAO Rong-ge, JIN Shuai-shuai
(Shaanxi Key Laboratory of Advanced Stimulation Technology for Oil & Gas Reservoirs, College of Petroleum Engineering, Xi’an Shiyou University, Xi’an 710065, China)
Many factors affect the pipeline corrosion rate, constituting a highly complex corrosion system; thus, accurately predicting the pipeline corrosion rate is difficult. A single back propagation (BP) model can easily fall into the local optimum due to an improper selection of the initial weight and threshold value. To address this problem, the whale optimization algorithm (WOA) algorithm is introduced for BP neural network optimization to predict the corrosion rate of a submarine pipeline. Then, it is compared with the GA and PSO algorithms to optimize the BP prediction model to verify the prediction effect and feasibility of the WOA-BP model. The results show that the average absolute percentage and root mean square errors of the WOA-BP model are 3.689% and 0.1537, respectively, considerably lower than those of the single BP, PSO-BP, and GA-BP models. It has high prediction accuracy and stability and can provide decision support for corrosion protection in the submarine pipeline and flow guarantee of the oil and gas pipeline.
corrosion rate; WOA algorithm; BP model; GA algorithm; PSO algorithm
Aug. 23, 2021
[2019 Local Service Special Plan Project of Shaanxi Provincial Department of Education, No. 19JC034]
TG174
A
1000-3096(2022)06-0116-08
10.11759/hykx20210823003
2021-08-23;
2021-10-14
陕西省教育厅2019年度服务地方专项计划项目(19JC034)
肖荣鸽(1978—), 女, 陕西省兴平人, 教授, 博士, 主要从事天然气处理与加工、油气水多相流理论与应用研究, E-mail: xiaorongge@163.com
(本文编辑: 赵卫红)
