基于正交试验的橡胶混凝土单轴受压应力-应变全曲线研究*

2022-08-01李京军

工业建筑 2022年3期

付乾薛刚许胜李京军

(内蒙古科技大学土木工程学院，内蒙古包头 014010)

近年来, 我国汽车行业飞速发展, 截至2021年3月，全国汽车保有量达到2.87亿辆。随着汽车保有量的快速增长，废旧轮胎数量也迅速增加，而我国废旧轮胎利用率较低。有数据显示，2020年我国废旧轮胎产量超过1 000万吨，回收利用率约60%，有近400万吨废旧轮胎未回收利用，不仅造成资源浪费，同时给环境带来严重污染。若能合理回收利用废弃轮胎，不仅能够缓解我国橡胶资源人均匮乏的窘境，而且能够改善环境质量，实现经济效益和生态效益双赢。

橡胶混凝土是在普通混凝土基体中掺入橡胶集料的一类新型混凝土，简称为CRC,其具有良好的韧性和延性，优良的抗冲击性能和弯曲性能，但抗压强度低。将其用于道路工程，可充分发挥其减振、降噪、耐磨等多方面的优势，对资源回收利用也起到了积极的作用[1-5]。Topcu以45%的橡胶粉取代集料掺入混凝土中进行抗压与抗拉强度试验，研究表明，橡胶混凝土抗压强度接近基准混凝土强度的50%，抗拉强度也出现明显下降[6]。Benazzouk等对橡胶水泥复合材料的物理性能进行了研究，发现橡胶颗粒改善了复合材料的抗折强度和变形能力，随着橡胶掺量的增加，抗折强度有着不同程度的提高，但抗压强度降低[7]。刘日鑫等采用废旧橡胶颗粒分别以 0、2%、4%、6%、8%、10%、15%、20%、30%、40%体积分数外掺到混凝土中进行抗压及抗折强度试验[8]，结果表明：橡胶掺量对混凝土强度的影响十分显著，低掺量的橡胶混凝土强度减小较慢，橡胶掺量超过10%时，随着掺量的增加，强度减小迅速。潘东平以橡胶掺量和橡胶粒径为变量，研究得出橡胶混凝土的本构方程[9]。

粉煤灰在一定程度上可以提高混凝土的密实度，减少混凝土内部因水化产生的热量，这在混凝土的耐久性方面表现的较为明显。

以正交设计方法配置橡胶混凝土，对其进行单轴受压试验，研究橡胶混凝土的破坏形态。利用极差法分析橡胶混凝土力学性能对水胶比、橡胶替代率、橡胶粒径、粉煤灰替代率4个因素的敏感性，探讨橡胶替代率对橡胶混凝土峰值应力、峰值应变、弹性模量、极限应变、韧性指数、脆性指数的影响机理，提出这些力学性能指标与橡胶替代率的函数关系，并建立橡胶混凝土的应力-应变模型，以期为橡胶混凝土的工程应用提供试验和理论依据。

1 试验概况

1.1 试件设计及制作

为研究不同水胶比、橡胶替代率、橡胶颗粒目数以及粉煤灰替代率下橡胶混凝土单轴受压应力-应变全曲线，设计了12 组配合比(含 3 组不同水胶比的普通混凝土)、尺寸为150 mm×150 mm×300 mm的试件，每组3个试件，同时制作了100 mm×100 mm×100 mm的立方体试件，以测得混凝土立方体抗压强度。试件制作方法参考GB/T 50080—2016《普通混凝土拌合物性能试验方法标准》。使用HJW-60型单卧轴试验室混凝土搅拌机对CRC进行搅拌，搅拌步骤如下：先将砂、石子和水泥投入搅拌机内搅拌均匀，再加入橡胶颗粒继续搅拌至均匀，然后再加入的70%左右的水，搅拌10～20 s，最后加入外加剂和剩余水，搅拌2～3 min，直到拌和均匀。将搅拌好的混凝土灌入试模中，经过振捣后在标准养护条件下养护28 d。

1.2 原材料

选用P·O 42.5水泥，强度为42.5 MPa，其相关性能指标见表1。橡胶粉采用20，50，80目橡胶颗粒。3种橡胶粉表观密度分别为1 050,1 020,890 kg/m3，具体物理性能见表2。粉煤灰用量为水泥含量的10%和20%，材料属性见表3。碎石采用5～25 mm连续级配，堆积密度为1 550 kg/m3，表观密度2 703 kg/m3。中砂采用普通河沙，最大粒径为5 mm，表观密度为1 530 kg/m3，细度模数为2.5，符合GB 14684—2011《建设用砂》的要求。依据GB 14684—2011进行砂子级配分析。外加剂采用聚羧酸高性能减水剂，减水率不小于25%。水采用普通自来水。

表1 水泥物理性能Table 1 Physical properties of cement

表2 橡胶集料物理性能Table 2 Physical properties of rubber aggregate

表3 粉煤灰材料属性Table 3 Material properties of fly ash

1.3 配合比设计

试验以水胶比为0.35的普通混凝土为基准，砂率为 43%。采用4因素3水平(34)的正交试验表，因素水平的选取见表4。考虑到重载要求，基准混凝土按照表5(n-0-0.35)组进行配制。按照各性能指标需要进行因素水平组合制备不同配合比的 CRC试件。采用橡胶粉等体积替代砂的方式掺入到混凝土中，根据正交试验设计的因素水平组合方案，最终得到9组不同配合比的CRC设计，见表5。

表4 正交试验因素和水平Table 4 Orthogonal test factors and levels

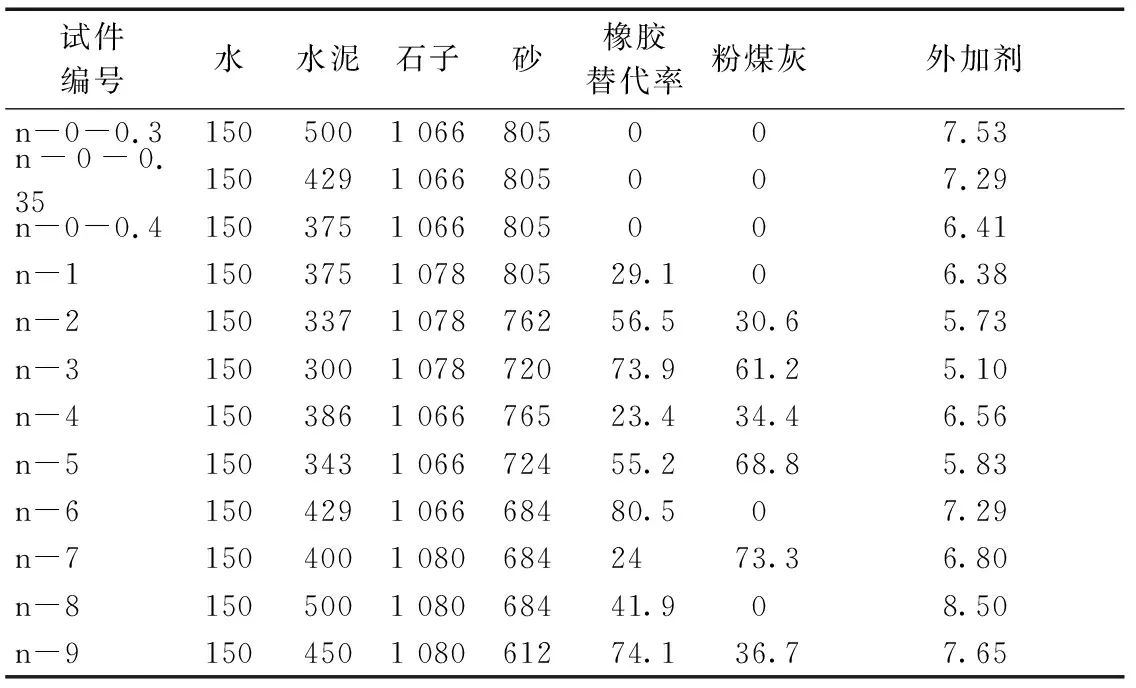
表5 橡胶混凝土配合比Table 5 Mix proportion of rubber concrete kg/m3

1.4 试验方法

棱柱体受压试验在微机控制电液伺服压力机上进行，用两个1 000 kN的液压千斤顶作为附加刚性元件，增加试验装置的整体刚度，以防混凝土突然破坏，该试验装置能够测得混凝土受压应力-应变曲线下降段。在试件两侧放置两个位移计以测量竖向位移，另外两侧分别在竖向和横向的中心线处粘贴混凝土应变片用于以测量应力-应变曲线上升段混凝土的应变。在应力达到约75%极限应力之前，试验加载速度为0.01 mm/s；在应力达到75%极限应力之后，试验加载速度调整为0.003 mm/s。试验中采用DTS-530型高速静态数据采集仪自动采集。立方体抗压强度值为该组3个混凝土试件立方体抗压强度的算术平均值，按照GB/T 50081—2019《混凝土物理力学性能试验方法标准》，骨料粒径不大于30 mm可以使用非标准试件，因此试验值需要乘以修正系数 0.95，得到橡胶混凝土立方体最终抗压强度。

2 试验结果及分析

2.1 试验现象和破坏形态

橡胶混凝土和普通混凝土试件破坏形态如图1所示，两者破坏形态和破坏机理有所差别，主要分为4个阶段：

a—普通混凝土； b—橡胶混凝土。图1 单轴受压试件破坏形态Fig.1 Failure modes of specimens under uniaxial compression

1)弹性阶段：在试验加载初期，由于此时应力较小，橡胶混凝土试件变化不大，变形主要是骨料和水泥基体受力产生的弹性变形[10]，初始微裂缝变化以及水泥的黏性流动产生的影响很小。此阶段混凝土内部微裂缝扩展与已有微裂缝的压缩平衡，处于相对稳定期，该阶段的橡胶混凝土变形略高于普通混凝土变形。

2)内部裂缝稳定扩展阶段：随着荷载的逐渐增加，由于水泥胶体黏性流动和内部微裂缝的扩展，加之橡胶颗粒被逐渐压缩，其对试件弹性性能的增强作用减弱，试件持续发出碎裂的声音，说明试件内部裂缝逐步稳定扩展，整体仍处于稳定状态。与普通混凝土相比，由于橡胶颗粒与其他骨料和水泥浆体的黏结作用相对较弱，该阶段橡胶混凝土试件内部裂缝发展相对较快。

3)外部裂缝扩展阶段：荷载继续增加，当试件所积蓄的弹性应变能持续大于裂缝发展所需要的能量，便进入裂缝快速发展的不稳定阶段[11]，试件内部原有裂缝逐渐扩展、贯通，新裂缝大量产生，表面裂缝开始显现并逐渐增大，上端与下端开始出现多个细小裂缝，混凝土内部水泥砂浆与骨料逐渐失去黏结作用，竖向压缩应变增长较快，试件侧向膨胀，试件的竖向裂缝逐渐增多，随后混凝土达到峰值应力。这个阶段，橡胶混凝土的裂缝发展更加充分，橡胶替代率高的试件，加荷上升速度相对较慢。

4)破坏阶段：达到峰值应力后，试件的承载能力随应变增长逐渐减小，出现应变软化现象[12]，此阶段试件表面出现一些不连续的纵向裂缝，裂缝越来越多，裂缝宽度也有所增加，内部结构的破坏越来越严重，荷载的有效传力路线不断减少，混凝土骨料与水泥浆体之间的胶结力、摩擦力等黏结作用被破坏[11]，试验机读数下降速度加快，直到试件失去承载能力。橡胶混凝土试件荷载下降速度较普通混凝土下降速度均匀且缓慢，破坏形态较普通混凝土完整，体现出更好的变形能力。

2.2 橡胶替代率对CRC力学性能的影响

通过极差法分析正交试验结果，直观地排列出橡胶混凝土的峰值应力、峰值应变、弹性模量、极限应变、韧性指数、脆性指数6种力学性能对水胶比、橡胶替代率、橡胶粒径、粉煤灰替代率4个因素变化的敏感性，极差分析结果见表6。根据极差分析结果可以看出，4个因素中橡胶替代率对橡胶混凝土力学性能影响最大，主要分析在不同的水胶比下，橡胶替代率对橡胶混凝土力学性能的影响规律。

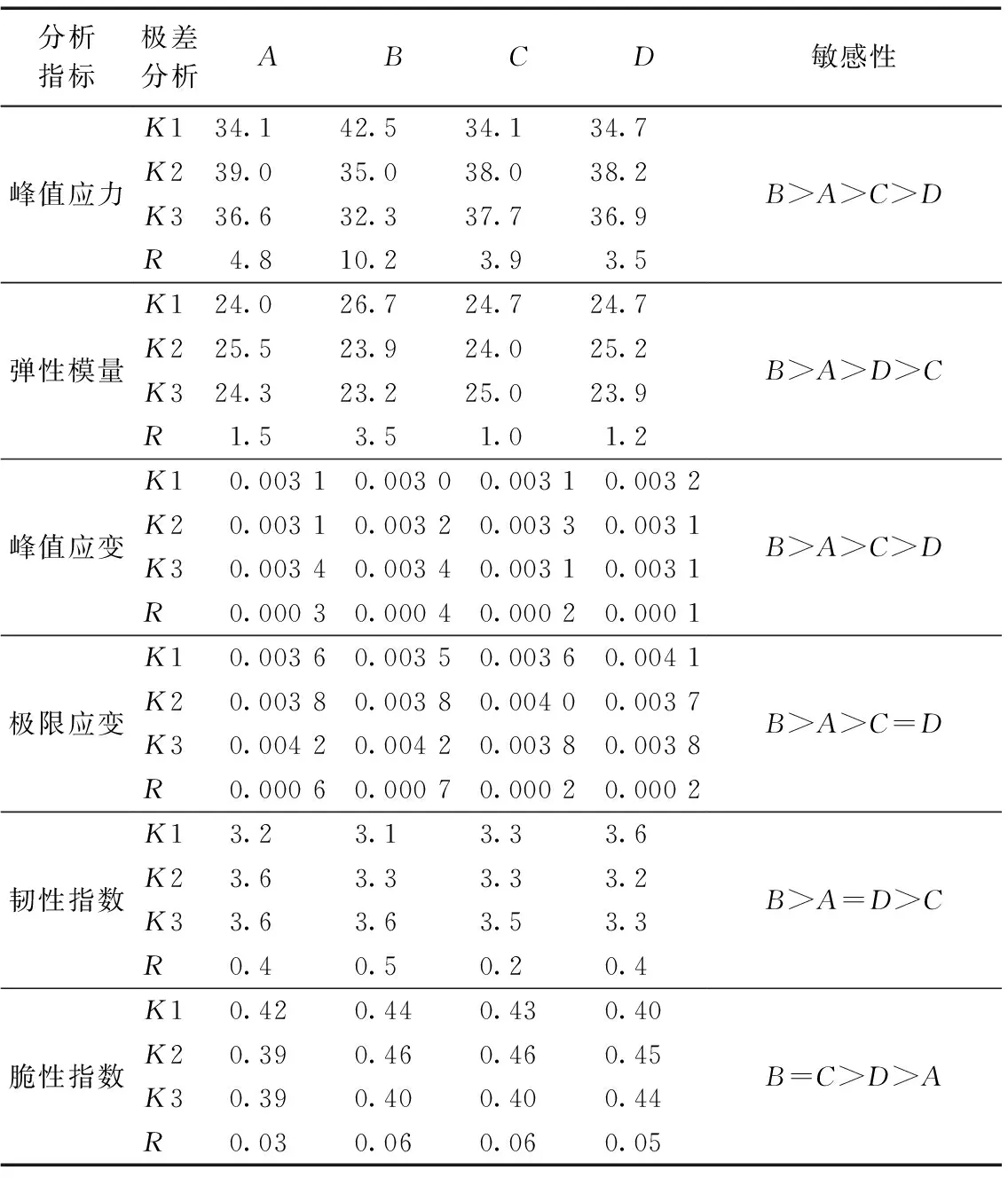
表6 极差分析结果Table 6 Range analysis results

1)峰值应力。橡胶混凝土的峰值应力主要取决于水泥砂浆的强度和骨料与水泥基体的界面连接[13]，一般情况下橡胶颗粒与水泥基体的连接情况较差。由图2a可知：橡胶混凝土的峰值应力明显低于普通混凝土的峰值应力；随着橡胶替代率的增大，橡胶混凝土的峰值应力逐渐减小，说明橡胶替代率的增加会降低橡胶混凝土的强度。以水胶比0.35为例，橡胶替代率从5%增加至10%，峰值应力下降了26.7%。

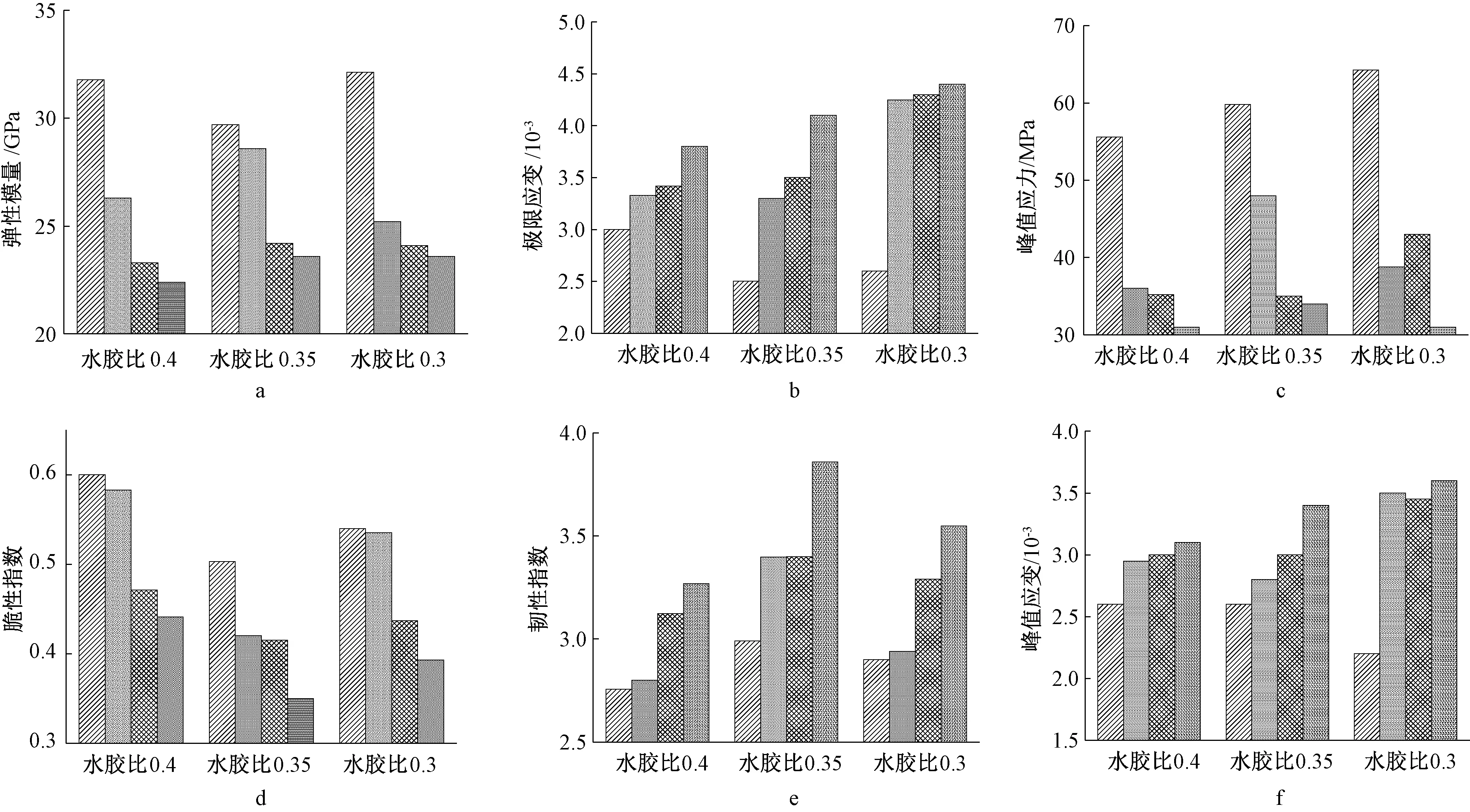
a—橡胶替代率对峰值应力的影响； b—橡胶替代率对峰值应变的影响； c—橡胶替代率对弹性模量的影响； d—橡胶替代率对极限应变的影响； e—橡胶替代率对韧性指数的影响； f—橡胶替代率对脆性指数的影响。橡胶替代率0%；橡胶替代率5%；橡胶替代率10%；橡胶替代率15%。图2 橡胶替代率对力学性能指标的影响Fig.2 Influence of rubber replacement ratios on relevant parameters

2)峰值应变。峰值应变也是橡胶混凝土应力-应变模型的重要参数，主要受混凝土强度、加载速率，截面尺寸和约束条件等因素影响[10]。橡胶替代率对橡胶混凝土峰值应变的影响如图2b所示，由图可知：橡胶混凝土的峰值应变高于普通混凝土的峰值应变，且随着橡胶替代率的增加，橡胶混凝土的峰值应变逐渐增大；水胶比为0.35，橡胶替代率从5%增加到15%时，峰值应变增加了21.5%。说明随着橡胶替代率的增加，橡胶混凝土的变形能力增强，且体积变形率逐渐增大。

3)弹性模量。弹性模量用于衡量材料抵抗弹性变形能力。橡胶替代率对橡胶混凝土弹性模量的影响如图2c所示：随着橡胶替代率的增加，橡胶混凝土的弹性模量逐渐减小，在加载初期阶段，橡胶替代率越高，试件的弹性变形越明显，当水胶比为0.35，橡胶替代率从5%增加到10%时，弹性模量降低了15.4%。原因在于，混凝土弹性模量与骨料弹性模量和表面构造有明显的相关性，橡胶颗粒为弹性材料，弹性模量相对低，因此橡胶混凝土的弹性模量随着橡胶替代率的增加而降低。

4)极限应变。极限应变是应力-应变曲线重要的特征点，对工程应用有重要的参考价值，橡胶替代率对橡胶混凝土极限应变的影响如图2d所示：随着橡胶替代率的增加，橡胶混凝土的极限应变呈增大趋势。水胶比为0.35，橡胶替代率从10%增加到15%时，极限应变增加了32.3%。表明随着橡胶替代率的增加，橡胶混凝土的延性得到提高。水胶比为0.35，橡胶替代率为10%时，试件极限应变偏高，主要是因为该配合比下橡胶混凝土的稳定性相对较好。

5)韧性指数。在塑性变形和破坏过程中，韧性表示材料吸收能量的能力，一般来说，材料韧性的大小主要体现在两个方面：材料的极限强度以及材料破坏时变形的大小；韧性指数为3倍峰值应变与1倍峰值应变所对应的力-应变曲线包围的面积之比。橡胶替代率对橡胶混凝土韧性指数的影响如图2e所示。水胶比为0.4，橡胶替代率为10%时，峰值应变较大，未测到3倍峰值应变点，以峰值应变点后曲线全部下降段与应变轴围成的面积来代替曲线峰值应变点到3倍峰值应变点之间曲线与应变轴围成的面积。图2e表明，提高橡胶替代率，可以增强橡胶混凝土的韧性，使其在破坏时极限强度相对较小，而破坏时的变形相对较大。实际工程应用中，在满足强度要求的情况下，可考虑用橡胶颗粒替代纤维等增韧材料。

6)脆性指数。实际工程中，要尽可能避免发生脆性破坏。有的材料极限强度较小，破坏时变形较大，呈现延性；而有的材料极限强度高，破坏时变形较小，表现为脆性。脆性指数为1倍峰值应变与1倍到3倍峰值应变对应的应力-应变曲线围成的面积之比。橡胶替代率对橡胶混凝土脆性指数的影响如图2f所示：脆性指数随橡胶替代率的提高而渐渐降低，水胶比为0.4时，橡胶替代率从5%增加至10%，峰值脆性指数降低了19.2%。说明增加橡胶替代率可以降低混凝土的脆性。由韧性指数I和脆性指数B的关系(I=1+1/B)可以再次证明，橡胶替代率的增加可以提高橡胶混凝土的韧性。

2.3 橡胶混凝土应力-应变关系分析

橡胶混凝土的应力-应变曲线如图3所示。总体来看，随着橡胶替代率的增加，应力-应变曲线逐渐呈现出“矮胖”的形状，曲线的饱满程度明显提高。在加载初期，0.5fc(fc为峰值应力)之前，应力-应变曲线接近直线，这一阶段，随着橡胶替代率的增加，曲线斜率逐渐减小，说明橡胶颗粒的掺入降低了混凝土的刚度；与普通混凝土相比，由于橡胶颗粒本身具有的良好弹性，再加上试件内部的缺陷和空隙较少，使得橡胶混凝土的弹性阶段比普通混凝土弹性阶段维持较长。

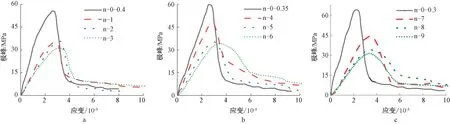
a—水胶比0.4； b—水胶比0.35； c—水胶比0.3。图3 橡胶混凝土应力-应变全曲线Fig.3 Full stress-strain curves of rubber concrete

在0.5fc～fc之间，应力-应变关系偏离直线，应变的增长速度快于应力的增长速度。曲线斜率逐渐减小，但减小速率有所差别，总体来看，橡胶替代率越大，曲线斜率减小的速率越快，且曲线顶端也逐渐趋于圆滑，说明随着橡胶替代率的增加，橡胶混凝土的韧性逐渐增强、脆性得到明显改善。

在曲线整个上升段可以看出，随着橡胶替代率的增加，橡胶混凝土对荷载的承受能力下降，但变形能力得到了提高，应力-应变曲线原点至峰值点的割线模量逐渐减小，峰值割线模量和弹性模量的比值E′C/EC逐渐减小。

峰值应力之后，在曲线下降阶段，应力下降加快，直到下降段曲线出现“拐点”，曲线开始凸向应变轴，这时应力下降缓慢，最后趋于稳定。总体来看，橡胶替代率高的试件破坏时发生的位移比橡胶替代率低的试件要大，延性破坏和较高的耗能能力等特点逐渐明显。对比来看，不同橡胶替代率的橡胶混凝土下降段形状有较大差异，总体呈橡胶替代率越高，下降段越缓，即应力下降相同幅度时橡胶替代率越高的试件变形越大，延性越好；反之越低，越陡，越小，越差。

下降段的存在和相对较缓表明受压破坏后的橡胶混凝土仍保持一定的承载能力，这在工程应用可以更好的承受荷载，降低发生脆断的风险，但下降段中趋于稳定的后半段已经失去工程意义。其中值得一提的是，在观察各试件的各应力-应变曲线下降段可以看出，在下降段的后一部分，应力出现了幅度较为明显的骤回，这是由于橡胶颗粒被压实所导致的。

2.4橡胶混凝土力学指标随橡胶替代率的变化规律

前文分析了橡胶替代率对各种力学性能的影响规律，但在实际工程应用中要有一定的数据或者计算模型作为参考，从而也对理论分析做出必要的支持。现将各种力学性能及各种影响因素做无量纲处理，运用MATLAB软件进行回归分析，得出橡胶替代率和各力学性能间函数性质的内在联系。

1)峰值应力。普通混凝土轴心抗压强度与立方体抗压强度的比值fc/fcu在0.7～0.92，本文测得橡胶混凝土轴心抗压强度与立方体抗压强度的比值fc/fcu在0.69～0.83，略低于普通混凝土的强度比值。主要原因在于，掺入橡胶颗粒后，试件强度和弹性模量均有所降低，且随着橡胶替代率的增大，立方体抗压强度也随之逐渐降低，试验机加载板对橡胶混凝土的环箍作用对强度的影响相对增强，致使立方体的抗压强度有所增高，而橡胶混凝土的单轴抗压强度稍有降低，故两者比值相对较低。回归分析得到橡胶混凝土棱柱体抗压强度和立方体抗压强度比值fc/fcu与替代率r的换算关系及轴心抗压强度与立方体抗压强度的换算关系：

fc=75.62r+1.28fcu-31.74

(R2=0.94)

(1a)

fc=0.58fcu+8.9 (R2=0.96)

(1b)

2)峰值应变和极限应变。由于橡胶混凝土自身的初始弹性模量较小，在强度相同情况下，橡胶混凝土的峰值应变和极限应变均大于普通混凝土，故原有的混凝土峰值应变计算模型不再适用于橡胶混凝土，拟合得出橡胶混凝土应变与橡胶替代率的函数关系为[14]：

εc=-2.33×10-3r+0.93εcu-1.32×10-4

(R2=0.97)

(2)

式中：εc为峰值应变；εcu为极限应变。

3)弹性模量。从应力-应变曲线关系的角度来看，弹性模量和韧性指数有着密切联系，在峰值应力相同时，初始弹性模量的大小和峰值应力点前应力-应变曲线与应变轴围城的面积有明显相关性，弹性模量越大，围成的面积越大，反之越小。这就说明弹性模量EC和韧性指数I呈正相关关系，拟合得出弹性模量、韧性指数和橡胶替代率的关系为：

EC=-67.8r+4.58I+16.41 (R2=0.96)

(3)

4)韧性指数和脆性指数。由韧性指数和脆性指数的关系(I=1+1/B)可将两者与橡胶掺量的函数关系综合分析，拟合得出韧性指数、脆性指数及橡胶掺量三者间的函数关系：

B=4.19×10-2r-0.22I+1.16 (R2=0.98)

(4)

3 应力-应变全曲线模型

3.1 模型确定

近年来国内外学者对橡胶混凝土的力学性能开展了广泛而深入的研究，但对橡胶混凝土单轴受压应力-应变本构模型的研究仍然较少，难以准确描述橡胶混凝土的力学性能和破坏特征，在工程应用中计算结果的可靠度较低。采用3种混凝土单轴受压应力-应变全曲线模型，包括Yang模型[15]、Saenz模型[9]、过镇海模型[16]。采用Matlab软件并结合试验结果和理论分析对各试件应力-应变曲线进行拟合。

Yang提出的表达式具有数学表达式简单、上升段与下降段采用同一个方程以及参数计算较为简便的特点，其表达式为：

(5)

其中y=σ/fc，x=ε/εc

式中：σ为应力；fc为橡胶混凝土峰值应力；ε为应变；εc为混凝土峰值应变；β1是确定曲线上升段和下降段斜率的关键参数。

关于β1有:

β1=0.20exp[0.73(10/fc)0.67(wc/2 300)1.17]ε≤εc

(6a)

β1=0.41exp[0.77(10/fc)0.67(wc/2 300)1.17]ε>εc

(6b)

0.4(Xa)β1+1+(0.4-Xa)β1-Xa=0ε≤εc

(7a)

0.4(Xd)β1+1+(1-2Xd)β1-Xd=0ε>εc

(7b)

其中Xa=0.4fc/Ecεc，Xd=ε0.5/εc

式中：ε0.5为曲线下降段最大应力下降 50%时的极限点；wc为混凝土密度，取2 500 kg/m3。

1964年,Saenz 提出的混凝土本构关系，该表达式也是上升段与下降段采用同一个方程，其表达式为：

y=x/(c1+c2x+c3x2+c4x3)

(8)

其中y=σ/fc，x=ε/εc

式中：σ为应力；fc为混凝土峰值应力；ε为应变；εc为混凝土峰值应变；c1、c2、c3、c4均为常数，可根据应力-应变曲线的特征点确定。

过镇海提出的混凝土单轴受压应力-应变关系表达式为分段形式，以峰值应力点为界限，分为上升段和下降段，上升段为多项式函数，下降段为有理分式函数，其表达式为：

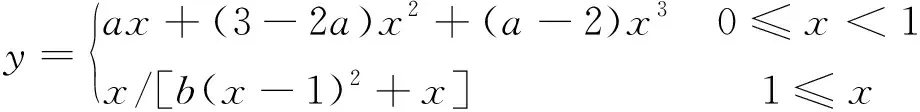
(9)

其中y=σ/fc，x=ε/εc

式中：σ为应力；fc为橡胶混凝土峰值应力；ε为应变；εc为混凝土峰值应变；a为混凝土原点切线模量与峰值割线模量比值，a值越大，材料延性越好；b为下降段曲线的陡峭程度参数，b值越大，下降段曲线越陡峭，材料脆性越大。文献[15]对该式中的参数做了详细的分析。

对试验数据进行无量纲化处理，再利用以上3个模型对本文的试验结果进行拟合，结果见图4。拟合结果表明：Yang模型、过镇海模型和Saenz模型三者均与试验曲线上升段拟合程度较高，相关系数均大于0.97，但过镇海模型中参数a不满足该模型的允许范围，Saenz模型上升段高估了橡胶混凝土的应力，出现了y=σ/fc大于1的情况，不符合应力-应变关系曲线特征。对于下降段，由于橡胶混凝土区别于普通混凝土的一些特殊性质，过镇海模型和Yang模型与试验曲线的拟合程度均不高，只有Saenz模型与试验曲线的拟合程度较高，相关系数均大于0.98，并且符合应力-应变关系曲线特征。

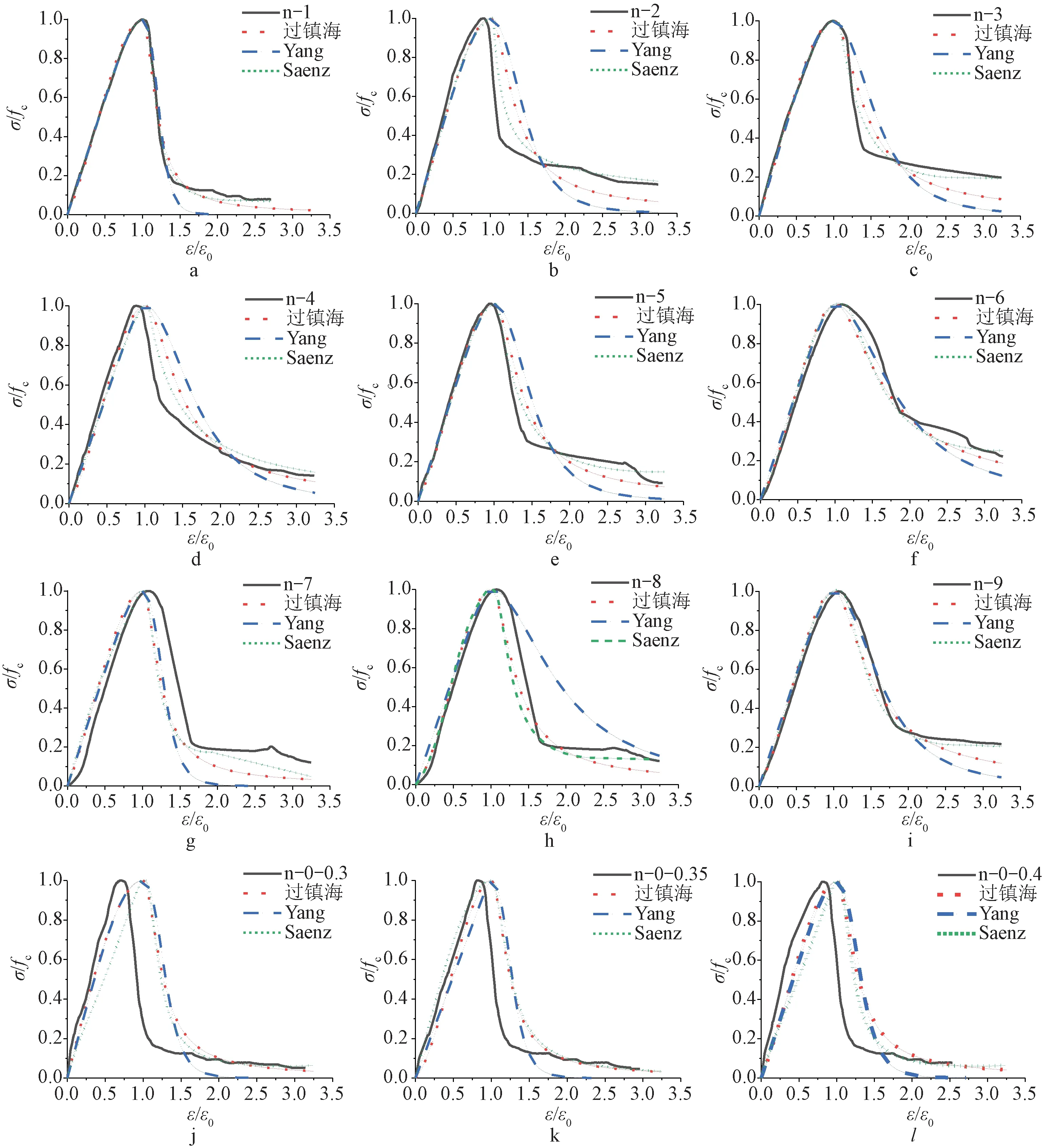
a—n-1； b—n-2； c—n-3； d—n-4； e—n-5； f—n-6； g—n-7； h—n-8； i—n-9； j—n-0-0.3； k—n-0-0.35； l—0-0-0.4。图4 拟合结果Fig.4 Fitting results

根据橡胶混凝土的应力-应变关系试验结果、3个混凝土本构模型的拟合结果以及橡胶混凝土的自身特点，建议采用函数类型为分段式的应力-应变全曲线方程对橡胶混凝土单轴受压应力-应变全曲线进行描述。上升段采用Yang模型，下降段采用Saenz模型，这种修正模型不仅能准确描述橡胶混凝土的应力-应变关系，还能简化曲线上升段的计算，同时又能较好地描述下降段的曲线特征，表达式为：

(10)

3.2 模型参数计算分析

将确定模型中的参数β1和c1、c2、c3、c4与轴心抗压强度和立方体抗压强度进行无量纲回归分析，确定各参数的计算表达式如下：

β1=3.04fc-1.69fcu-24.65 (R2=0.96)

(11a)

c1=-30.85fc-18.95fcu-245.78 (R2=0.98)

(11b)

c2=66.17fc-40.67fcu-529.08 (R2=0.98)

(11c)

c3=-44.47fc-27.35fcu-357.22 (R2=0.98)

(11d)

c4=8.89fc+5.48fcu+71.08 (R2=0.99)

(11e)

参数β1和c1、c2、c3、c4与轴心抗压强度和立方体抗压强度的函数关系的相关系数均接近1，根据拟合出的模型系数与强度的关系，再次做出橡胶混凝土的应力-应变曲线，与试验得出的曲线进行对比，结果见图5，可见由模型参数关系式表达的曲线与试验结果曲线吻合良好，表明上述计算式可以较准确地反映橡胶混凝土的应力-应变关系。

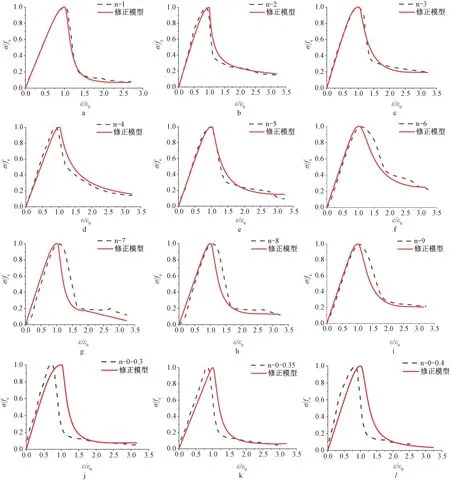
a—n-1； b—n-2； c—n-3； d—n-4； e—n-5； f—n-6； g—n-7； h—n-8； i—n-9； j—n-0-0.3； k—n-0-0.35； l—0-0-0.4。图5 修正模型与试验结果对比Fig.5 Comparisons between the modified model and the test results

为了更易理解所建立的应力-应变模型与橡胶混凝土特点之间的联系，特地将应力-应变模型参数与橡胶混凝土的韧性和脆性建立联系，以便更直观地了解橡胶混凝土的特性，表达式如下：

β1=-2 956.7+2 609.6B+545.7I

(R2=0.98) (12a)

c1=-2 217.9+2 145.0B+389.3I

(R2=0.99) (12b)

c2=4 467.3-4 384.0B+777.7I

(R2=0.99) (12c)

c3=-2 829.0+2 817.7B+487.5I

(R2=0.99) (12d)

c4=567.2-569.2B-97.1I

(R2=0.99) (12e)