深开挖后土体卸荷导致隧道隆起变形的算法*
2022-08-01王振峰徐明霞刘红霞
王振峰 赵 婷 徐明霞 刘红霞
(1.陕西国防工业职业技术学院, 西安 710300; 2.西安文昌历保信息科技有限公司, 西安 710065)
随着城市建设脚步加快,越来越多的地下空间被开发利用,目前地下空间的建设是城市建设中的重要组成部分。在地下空间大规模的开发过程中,基坑开挖施工造成的扰动不可避免。基坑开挖在施工过程中,会将大量的地下土进行转移,破坏周围土体原有的受力平衡情况,引起强烈的环境效应,邻近土地原有的应力场因受到破坏而发生变化,引起基坑底部发生土体隆起、墙后土体侧移、内外地表的土体沉降;此外,还会造成邻近建筑物的主体结构的变化[1-2]。隧道结构具有刚度比较小,抵抗外界荷载能力比价弱的特点,一旦当隧道的变形超过自身所能承受的极限,就会引发安全事故。由于地下空间的使用能很大程度上缓解用地的压力,所以对基坑开挖施工过程中的土体卸载对地下空间造成的影响进行分析研究十分必要,通过计算影响程度对基坑开挖施工项目进行控制是提高隧道安全的重要措施。
对既有隧道上方基坑开挖,国内外学者已在经验预测、理论分析、模型试验、现场实测以及数值模拟等方面进行了大量分析研究。
在经验预测上,俞剑龙等假设地铁隧道变形与土体位移一致,结合上海软土地区基坑案例,利用Boussinesq公式,利用残余应力法得到预测基坑开挖而产生的土体竖向向上的变形算式,但是没有考虑隧道刚度存在对土体影响,同时未考虑基坑开挖卸荷的影响深度[3]。曹力桥指出基坑开挖范围越大,产生的坑底回弹变形就越大[4]。代述兵等认为土体加固对隧道控制回弹变形最有影响,对监测数据进行了回归分析并建立了半经验的隧道回弹计算式[5]。在模拟试验上,周顺华等通过室内模型试验,对基坑开挖下既有隧道相关的土压力、弯矩和内径的工作机理进行了研究,并在此基础上提出求解隧道水平和竖向内力和变形的具体方法[6]。魏纲等通过离心试验分析了隧道开挖对既有管道的影响规律,试验中以排放同等量水体来模拟隧道开挖引起的土体损失,研究了管线埋深、地层损失率等因素对管线附加荷载和变形的影响规律[7]。
在理论分析上,当前可以将基坑开挖引起的土体变形分析方法分为正分析和反分析法两大类,其中的反分析法主要是依据大量的现场施工数据进行反推得出项目施工方案[8]。就当前已有的研究来说,利用正分析方法对隧道的隆起变形进行计算求解时,对于土体间的相互作用力的关注尚较缺乏,大多将隧道的变形认为是的竖向变形,缺少一定的工程实用性。在利用反分析法进行求解时,由于需要依赖于大量的现场施工数据,但是在实际施工过程中,由于基坑施工项目的地质状态、支护结构、开挖卸荷等情况比较复杂,含有大量的不确定因素,所以利用这种分析法得到的结果偏差可能也比较大。在对施工项目的数值进行模拟的时候多是利用弹塑性本构模型,这种方法不能考虑应力和应变水平对基坑开挖卸荷土体刚度造成的影响,所以实际的计算结果也存在着一定的偏差[9]。郭院成等基于弹性理论,采用两阶段法,利用分层总和法计算出隧道轴线处由于基坑土体开挖引起的土体位移,用高斯曲线来拟合,研究基坑开挖对下卧隧道竖向隆起的影响[10]。刘建文等将盾构隧道简化为Vlazov地基中的Timoshenko梁,对作用在下卧盾构隧道上的基坑开挖卸荷作用采用Mindlin解计算,建立基坑开挖引起既有下卧盾构隧道隆起变形的理论计算模型[11]。曾祥会等为了研究基坑开挖过程对邻近高铁桥墩竖向变形的影响,通过对2个邻近高铁桥墩的基坑工程进行实时自动化监测,采用基于叠加原理的薄层分层总和法编制高铁桥墩邻近荷载竖向变形影响计算软件PIAS,对计算结果与监测数据进行对比验证[12]。周泽林等将隧道视为弹性地下连续梁来分析隧道本身的受力和变形,推导了隧道与周围土体相互作用的有限元耦合平衡方程,建立了层状地基中基坑开挖对邻近隧道影响的耦合分析方法[13]。康成等采用不同地基模型计算隧道纵向变形时,对比实际监测数据和隧道纵向变形理论解,认为Kerr地基模型下理论解最为精确,Pasternak模型稍次,而Winkler模型的计算结果误差最大[14]。
在数值模拟上,李恒结合不同位移控制标准,采用PLAXIS有限元软件,通过改变隧道相对位置、围护结构变形模式等参数,计算了480个有限元模型[15]。陶宇等以上海某基坑工程为依托,对基坑降水进行数值模拟,显示相比跨层降水,逐层降水方案对隧道位移的控制作用更加显著[16]。张玉伟等采用有限元并结合一维固结理论和三维渗流理论分析越江隧道上方基坑降水对其隧道结构的影响,研究发现基坑降水将造成下方越江隧道的沉降,降水深度与其隧道沉降量呈线性变化关系[17]。
在现场实测上,徐中华等针对上海市闸北区大宁商业中心基坑工程邻近隧道处采取了一系列控制地铁隧道变形的措施,遵循时空效应原理来设计开挖工况,并通过实测数据表明基坑开挖对已运营地铁隧道产生了一定的影响[18]。许四法等结合上海地区一个典型的隧道旁侧开挖深基坑工程,分析表明开挖会引起隧道向基坑方向产生较明显侧移并使隧道断面呈横椭圆形状的变形,直接影响到隧道的使用功能和安全性[19]。杨建民等基于对数型地层沉降曲线算式和弹性地基梁理论,推导得到对数型地层沉降作用下地埋梁的变形及内力解析解,并应用有限差分法推导得数值解[20]。
综上所述,目前基坑开挖对既有下卧隧道影响研究尚存在以下问题:1)目前盾构隧道的土体损失引起的土体变形理论解方法已经比较成熟,而基坑开挖引起的土体损失目前鲜有文献涉及,同样基坑开挖引起的周围土体位移场以及隧道变形的计算更多地是采用统计数据拟合的经验式,并没有从原理上入手。2)目前的重点研究仍集中于下卧隧道变形方面,而关于基坑开挖卸荷对下卧隧道的附加应力研究尚不成熟。3)目前研究基坑开挖对下卧隧道变形很少考虑地下水的影响,鲜有考虑对基坑开挖前工程降水对下卧隧道变形影响的研究。
基于已有的研究结果,通过对基坑开挖后土体卸荷引起的隧道隆起变形,从土体对造成隧道变形的原因进行分析,借助两阶段分析法对基坑开挖后土体卸荷导致的隧道附加荷载和地基梁刚度变化进行分析,采用有限元分析方法对基坑施工过程进行了模拟分析,用以计算隧道变形的规律。
1 方法原理
1.1 基坑隧道变形因素分析
基坑施工土体开挖会使得基坑邻近土体的原始应力场发生变化,施工过程中基坑开挖面上发生土体卸荷的情况,则因这部分土体自重应力的释放,使其原有的应力场产生变化[21],促使其下土体产生竖直向上的位移,导致基坑底部发生隆起;在进行开挖时,周围土体会在应力场的作用下向着中间进行移动,发生位移,使得基坑周围的土体发生沉降,加剧了基坑底部隆起变形的程度。当基坑邻近隧道施工时,会使隧道原有的结构平衡破坏,使隧道发生变形。
基坑开挖工程导致隧道发生变形是多因素综合作用的结果,包括基坑施工的自身因素,土体特性、施工参数,施工方案,支护结构以及基坑降水等[22]。
1)基坑施工的自身因素作用。基坑工程的自身因素主要是来源于基坑的形状、深度、土体特性、基坑和隧道的相对距离等,这些因素会直接导致隧道的变形。郑刚等论证了通过对坑内地基加固可将因基坑开挖所引起的地铁隧道位移控制在20 mm以内,满足地铁变形控制标准,安全可行[23]。
2)支护结构。在进行基坑施工时搭建支护结构是必不可少的施工阶段,搭建支护结构是为了保证基坑施工的安全,支护结构会对土体施加附加应力使其产生相对位移,使得土体原有应力发生改变,会对隧道原有的结构稳定状态产生影响,导致其发生变形;刘继强等研究发现:围护结构变形同时也会引起隧道产生收敛变形及轨道高差变化,当围护结构最大位移为45 mm时,对于收敛变形,悬臂型模式引起的变化最小,内凸型和复合型居中,踢脚型最大。
3)基坑降水的影响。基坑降水是开挖施工的前期准备工作,地下水位降低会导致土体中的原有应力场产生变化,增加应力导致土体可能发生位移变形,最终导致隧道产生位移变形。张建斌发现:基坑降水引起上、下行线道床水平位移分别为9.08,5.6 mm,各占总位移量的82.5%和37.3%。因此,对控制地铁轨道结构变形而言降水工序是安全施工控制的关键阶段。
4)基坑开挖土体卸荷的影响。基坑在进行施工时会伴随着土体卸荷的现象,基坑开挖会促使土体周边的初始应力平衡状态产生变化,随着基坑开挖深度的不断增加,土体自重应力释放程度的加剧,导致基坑底部产生向上隆起的变形状态,基坑周围土体的原始状态受到破坏,改变区域内相应土体原有的位移和内力状态,使得隧道初始平衡状态被破坏,稳定性发生变化,基坑下方隧道出现隆起现象,基坑本身的隆起变形也会使得隧道的隆起变形加剧。梁荣柱等指出:开挖结束后到浇筑底板期间,隧道变形仍在不断增大,主要原因是底板施工期间经历强降雨,由于土体流变产生的时空效应,隧道变形不断增大; 浇筑底板后至隧道上方底板结构施工开始之时,左线拱顶由于上覆荷载的不同,导致最大变形约408 mm,增大约36%,右线隧道拱顶最大变形约6.65 mm,增大约58%; 随后进行结构施工,隧道受结构自重荷载作用下沉,至结构施工完成,左线隧道拱顶最大变形约3.4 mm,减小约20%,右线拱顶最大变形减小至5.4 mm,减小约20%[26]。
1.2 隧道隆起变形计算方法
当前对于隧道的隆起变形的计算通常采用的是两阶段分析法,可以将其分为两阶段应力法和两阶段位移法[27]。由于两阶段位移法相对来说缺乏一定的理论技术的支持,所以选择两阶段应力法对隧道的隆起变形进行分析。第一步是计算出基坑开挖工程邻近没有隧道时的土体附加荷载情况,第二步是将第一步计算出来的土体附加荷载移加到隧道上,再利用隧道土体之间的相互作用理论求解出隧道的变形情况。在计算前,首先对基坑施工的扰动因素和隧道进行假定:首先假设隧道的下覆土体是均质弹性的,对土体参数取加权平均值;其次假设隧道是架设在均质土体上方的弹性地基长梁,两者之间不会产生相对位移的情况;最后在进行计算时,第一阶段对扰动因素下的附加应力场进行分析,第二阶段对在附加应力场下隧道产生隆起变形情况进行计算。
基坑的形状一般可将其认为是矩形的,在施工过程中包含了四个侧壁和一个基坑底部等五个施工卸荷面,施工过程中,基坑底部卸荷面会承受土体自重应力的释放,产生一个竖直向上的均布荷载,在侧壁卸荷面上同样也会承受土体应力的释放,产生一个垂直于侧壁面的三角形水平方向的荷载[28]。将土体看作是均质弹性的半无限体,不对支护结构对卸荷应力的遮拦效应进行计算,则可以认为卸荷应力是完全释放的状态,则可以通过Mindlin解算法对基坑施工卸荷面上的附加荷载进行计算[29]。
假设作用于基坑卸荷面任意一点的应力为σ,对卸荷面竖直(z方向)和水平(x方向)上的附加荷载进行计算,通过叠加原理计算出作用于基坑所有卸荷面上的卸荷应力为:
σx=σxd+σx1+σx2+σx3+σx4
(1a)
σz=σzd+σz1+σz2+σz3+σz4
(1b)
式中:σxd为水平基坑底面卸荷应力;σzd为竖直基坑底面卸荷应力,σx1、σx2、σx3、σx4为水平方向上基坑四个侧壁上的卸载力,σz1、σz2、σz3、σz4为竖直方向上的四个侧壁面上的卸荷应力。
1.3 隧道隆起变形求解方法
不考虑土体位移场与隧道刚度之间相互作用时,可默认土体位移场的位移即为隧道位移,但是考虑到隧道具有一定的刚度,必然与周围土体位移场产生相互作用,考虑土体与隧道之间的接触和作用方式,弹性地基梁理论是比较常见的基坑开挖卸荷对下卧既有隧道影响的隧道-土体相互作用理论方法[30]。弹性地基梁理论将隧道看作架卧在均质弹性土体上的无限长梁,理论中的参数的选取尤为重要,比较常见的 Winkler 模型,为单参数弹性模型,Winkler 模型假设地基为一系列独立的弹簧,但是此模型中未考虑土体的剪切刚度,土体性质仅由弹簧刚度所决定[31]。考虑隧道剪切变形效应,隧道纵向变形下的解析解通常有两种方法,一种是考虑隧道模型复杂化,将单参数的 Euler-Bernoulli 弹性长梁用双广义位移参数的梁模型来替代,另外一种方法就是从隧道与土体之间的作用模型入手,在常见的 Winkler 模型基础上考增加剪切层使得土体弹性变形之间增加联系,如Pasternak 模型,或者引入应力或位移假定得到隧道-土体作用模型,而三参数模型是对两参数模型的进一步深化,比较具有代表性的为 Kerr 模型。该模型是对于双参素模型的进一步深化,所需要的约束条件同样也更多。通过差分法对这几种计算模型进行地基梁刚度系数矩阵的转换。
Winkler模型是单参素模型,在该模型中只需要考虑隧道土体层压缩因素,隧道与土体相互作用时的地基模型如图1所示。
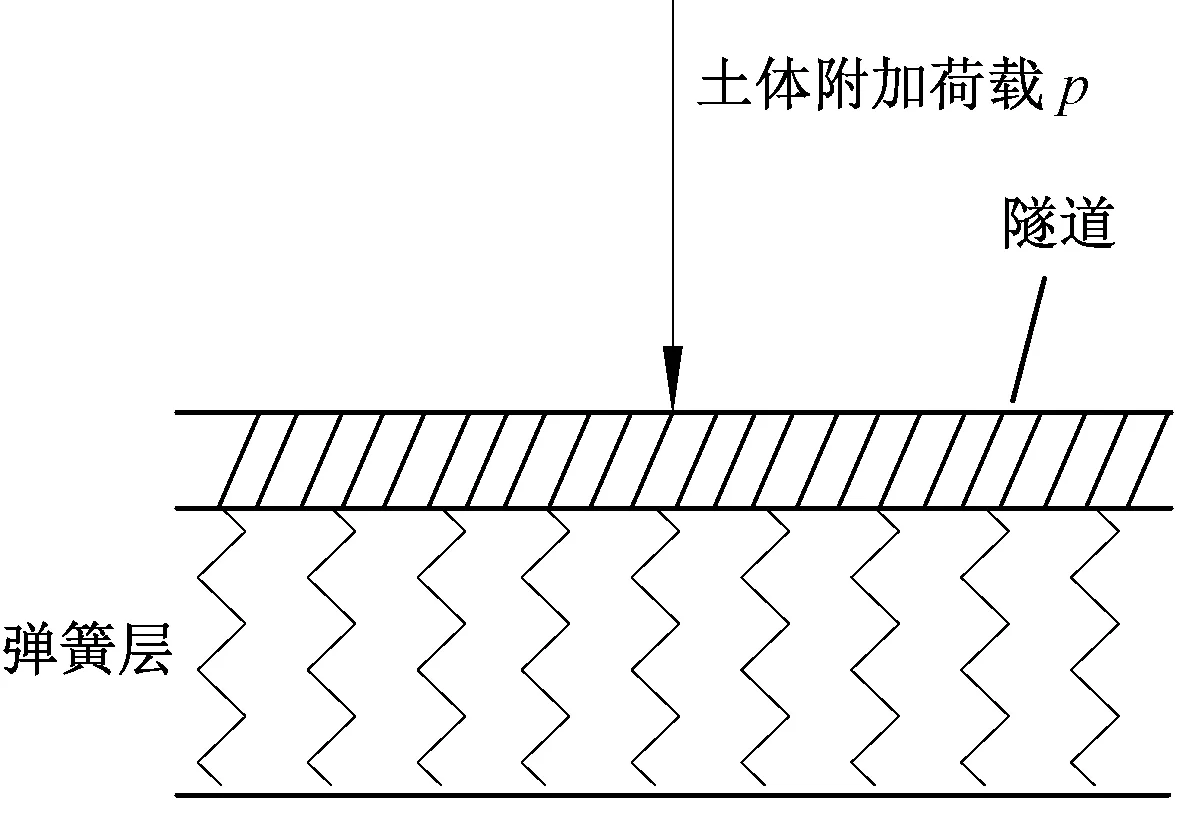
图1 Winkler模型地基梁示意Fig.1 The schematic diagram for the foundation beam of the Winkler model
Winkler模型的计算方法如下所示:
p=kw1
(2b)
式中:EI为隧道等效抗弯刚度;D为隧道外径;k为弹簧刚度系数;p为隧道与土体相互作用下的荷载;w1为土体位移;w为隧道的实际位移。
Pasternak模型是双参素模型,在进行计算时需要考虑土层和剪切变形效应,常用的隧道与土体进行相互作用的常见模型如图2所示。
Pasternak 模型推导式如下:
(3)
式中:G为剪切层剪切刚度。
将Winkler模型式和Pasternak 模型式通过差分法进行计算:
pi=α(w1)i+2+β(w1)i+1+γ(w1)i+
β(w1)i-1+α(w1)i-2
(4)
其中α=-EIG/(Dcl6)
β=6EIG/(Dcl6)+EI(c+k)/(Dcl4)
式中:α为基坑底部土体损失面形状系数,只与基坑的大小、长度、深度以及与土体点相对位置有关;β为侧壁的土体损失面形状系数,同样只与基坑形状、桩嵌入深度以及与土体点相对位置有关;i为剪切层的层数;γ为土体厚度。
对每个土体损失面简化方式下的位移乘以其土体坐标点向对应的形状系数叠加求和可得到整个任意一点的土体位移。
图3为Kerr模型中隧道与土体相互作用的常见模型,Kerr模型是三参素模型,是对双参素模型的进一步深化,其考虑了土层与剪切层之间的相互作用,在Kerr模型中,含有两个弹簧层以及一个剪切层,共有三个变形层,其平衡微分方程为:
(5)
式中:k为上部弹簧刚度;c为下部弹簧刚度。
将其代入相应的差分法式中进行计算:
pi=α(w1)i+3+β(w1)i+2+ξ(w1)i+1+ψ(w1)i+
ξ(w1)i-1+β(w1)i-2+α(w1)i-3
(6)
其中ξ=-15EIG/(Dcl6)-4EI(c+k)/(Dcl4)-G/l2
式中:ξ为下部弹簧层的土体损失面形状系数;ψ为土体厚度。
2 隧道隆起变形计算实例
基坑开挖会促使隧道产生隆起变形现象,其是一个复杂的过程,对市政隧道基坑施工引起的西安市地铁2号线隧道隆起变形进行计算。对西安已开通的地铁2号线区间隧道上方的综合改造工程的市政隧道工程对隧道的影响进行模拟计算。市政隧道采用明挖法施工,总长度867 m,共13节隧道箱涵,其中第6~8节隧道箱涵的基坑开挖最深约为9.5 m。市政隧道宽约41.0 m,高度约为5.0 m,采用单箱四室钢筋混凝土框架结构的方式,框架结构的顶板厚0.7 m,底板厚0.8 m,边墙厚0.8 m。地铁2号线盾构隧道顶覆土厚度约为1.3 m,隧道内径5.4 m,外径6 m,管片的厚度0.3 m,管片环宽1.5 m,区间隧道的最小埋深大概为12 m。市政隧道在地铁2号线盾构区间隧道顶部垂直穿过,对隧道造成影响的市政施工长度为236 m,盾构区间隧道的长度为37.05 m,市政隧道基坑底板到盾构隧道的拱顶的距离只有2 m。为了简化模型数值计算,选取第8节隧道箱涵所在位置进行模拟分析,定义模型尺寸设置为250 m×150 m×40 m。基坑尺寸为80.0 m×50.0 m×10.0 m,分5步开挖,开挖深度依次分别为3,2,2,2,1 m。建立了3个数值计算模型,在基坑的两侧及底部分别设置一条隧道,隧道半径为3.0 m,隧道中心距离基坑间距依次增加5.0 m。土体和管片采用solid实体单元,基坑连续墙采用板单元,连续墙与土体之间建立接触单元,地下连续墙外施加3层锚杆,锚杆采用梁单元,长度为15.0 m。地层采用修正摩尔-库仑模型描述,管片和连续墙采用弹性结构模型,接触单元符合库仑摩擦。模型底部采用固定位移约束,水平向边界均容许竖向位移,共有单元158 330个,结点117 416个。
分别用Pasternak模型,Winkler模型和Kerr模型对其进行计算。拟具体计算基坑5个卸荷面对隧道产生的附加水平线荷载和竖直线荷载,然后根据土体-隧道相互作用的三种差分法简化下的刚度矩阵模型,最终求出Winkler、Pasternak、Kerr模型下附加荷载下隧道产生的变形。同时建立基坑整体开挖数值模拟模型,进行对比。
为了对比上述这几种算法的计算优劣性,将分别用Pasternak模型,Winkler模型和Kerr模型对其进行计算,然后利用有限元分析方法对隧道的变形情况进行模拟求解,将利用三种模拟进行计算的结果与有限元解进行对比。
2.1 不同水平隧道位移变化
从三种模型位移计算结果(图4)来看,在基坑中心隧道纵轴坐标为0.0 mm处位移最大,竖向位移,Kerr和Pasternak的计算结果为92.8,93.4 mm,差距不大,而Winkler模型计算下竖向位移最大达到96.8mm,比前两者分别高了4.3%和3.6%,Winkler解计算结果最大的原因可能是由于Winkler 单参数假设下由于约束参数少,所以结果略微偏大。水平位移,Winkler模型下计算结果为9.55 mm,对比Pasternak和Kerr的8.16,8.08 mm,计算结果比后两者分别高出了14.6%和15.4%,三者中,Winkler解最大,Pasternak其次,Kerr解最小,原因是Winkler没有考虑土层剪切变形,参数设置相对较少,而Kerr模型里有三个参数,所以说地基梁刚度矩阵约束作用较大,则理论为位移相对较小。所以相对来说利用Kerr模型计算出来的结果更加准确,因此可以利用该模型对隧道变形的数值进行计算。
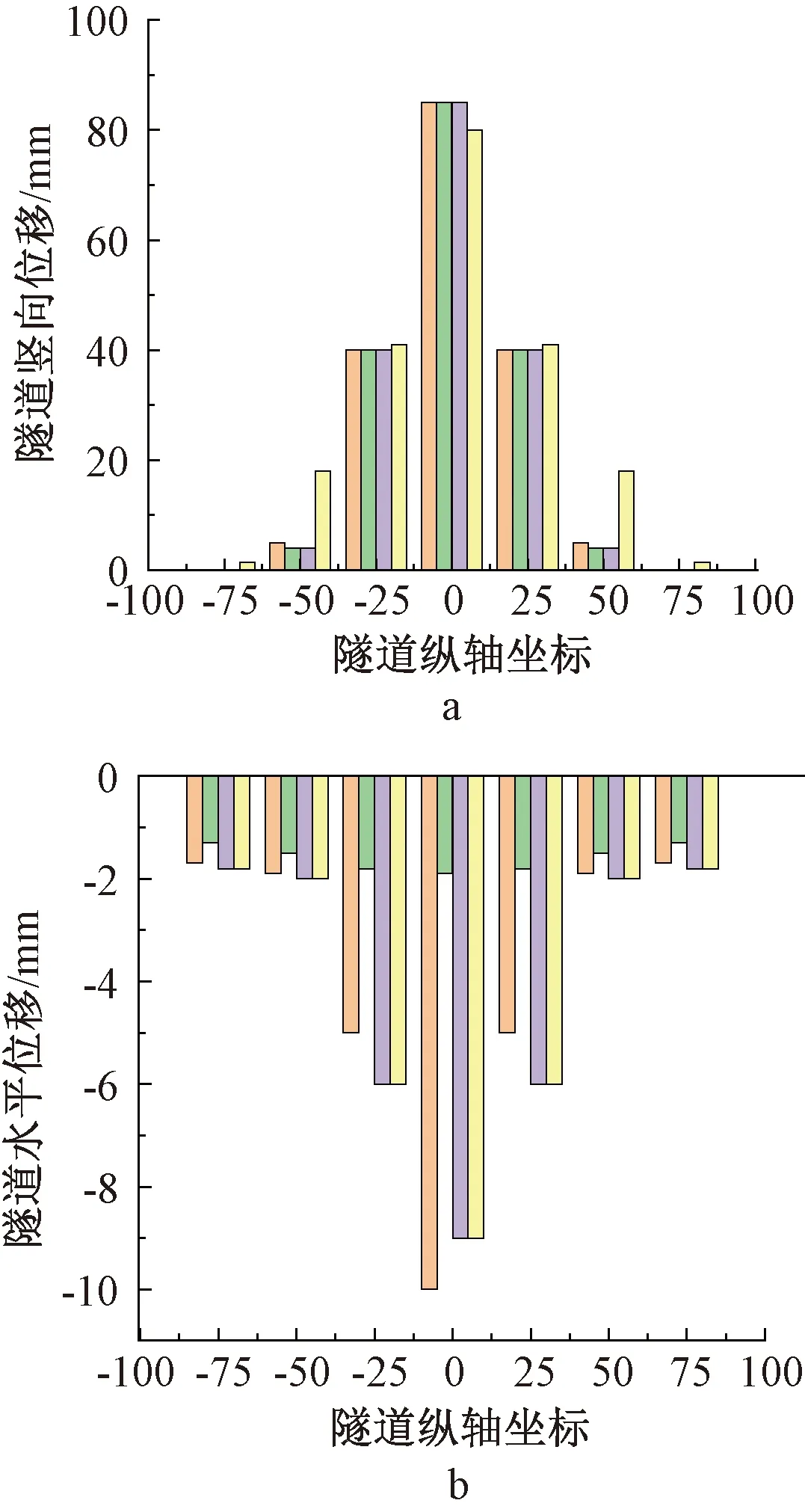
Winkler; Pasternak; Kerr; 有限元。图4 隧道不同方向位移情况Fig.4 Displacement of tunnels in different directions
2.2 数值模拟与三种模型计算结果对比分析
对比数值模拟与Winkler、Pasternak、Kerr三者的竖直位移和水平位移,如图5所示,可以发现数值模拟下最大竖向位移为6.6 mm,Winkler理论解比其大46.7%,而水平位移最大为1.68 mm,Winkler理论解比其大408.9%。首先数值模拟下两者的竖向位移和水平位移都比理论解小,这有由于理论解是应力卸荷完全释放的原因,而竖向位移变化幅度较小只有大约0.3倍,而水平位移变化了3.5倍。如图6所示,侧壁的围护结构对竖向附加荷载相对来说影响很小,对水平荷载影响相对很大,所以侧壁结构支护作用对隧道水平位移约束作用较大,对竖向位移约束作用较小,从而出现了水平位移和竖向位移幅度差如此大的计算结果。

水平位移; 竖直位移。图5 不同计算方法位移值对比Fig.5 Comparisons of calculating values in displacement calculating by different methods

a—水平附加荷载; b—竖向附加荷载。 基坑底面; X=-21; X=21; Y=-25.5; Y=25.5; Y=总和。图6 卸荷对隧道附加荷载的影响Fig.6 The influence of excavation on the additional stress of tunnels
对于隧道变形方面,通常以20 mm作为控制运营区间隧道变形允许值,竖向位移方面,Winkler 解其中在-35~35 m处竖向位移超过了允许值,需要重点布控对位移进行控制。而在Pasternak 和Kerr模型计算下,分别在-36~36 m和-37~37 m区间里面需要对竖向位移进行控制。而在水平位移方面,隧道整体位移最大值Kerr解为85.5 mm,属于可允许变形值,故此基坑开挖下水平位移方面可不进行布控。
2.3 有限元结果分析
计算基坑隆起如图7所示,基坑最大隆起量发生在(-5.25 m,0 m,12 m)处,最大基坑隆起值为12.07 cm。并不在基坑中心(0 m,0 m,12 m),分析原因:基坑开挖会对基坑底部下面土体产生向上的位移场,土体位移场作用在隧道上,导致隧道伴随土体产生附加的向上位移;但同样反过来,隧道具有一定刚度,会对基坑开挖引发的位移场产生一定的抵抗作用。隧道、土体之间的相互作用,共同形成了基坑开挖形成的土体位移场。
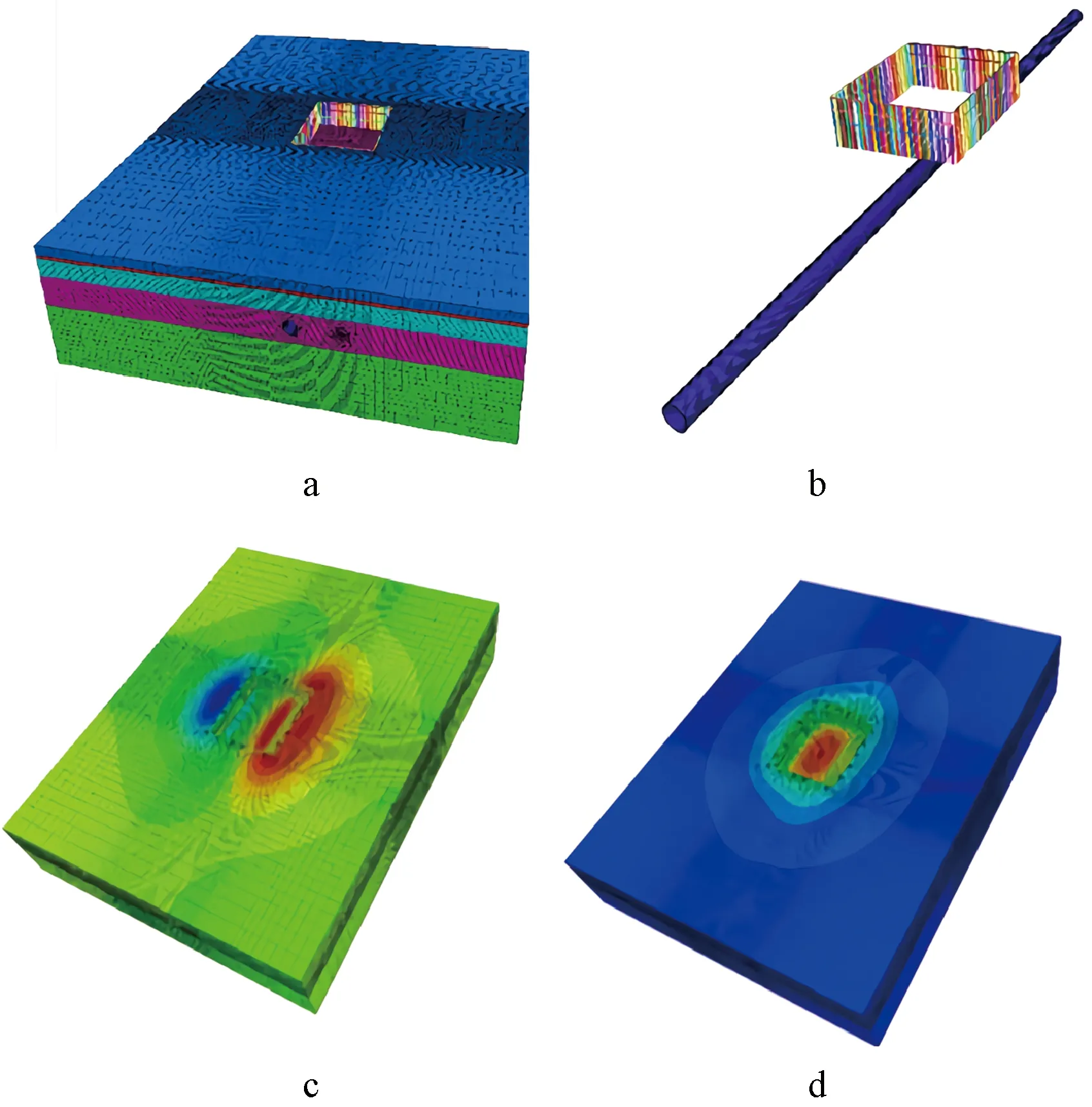
a—单隧道基坑开挖计算模型; b—单隧道与基坑之间的相对位置和支护结构; c—基坑开挖水平位移; d—基坑开挖的竖向位移。图7 有限元结果分析示意Fig.7 Analysis results by the finite element method
图8为有限元数据的验证结果,对Winkler、Pasternak、Kerr 和数值模拟四者竖向位移解得高斯曲线公式拟合,方差为5.098×10-2mm,确定系数为0.999 1,标准差:0.631 1 mm,通过四者拟合曲线可以发现,Winkler竖向位移拟合曲线在计算结果上最大,但标准差最小,数据离散程度最小,离散点更为集中。水平位移曲线和竖直位移规律相同。以数值模拟结果计算出来的水平位移来拟合高斯曲线,方差为1.292×10-2mm,确定系数为0.187 5,标准差为0.317 7 mm。可以看出曲率半径方面在-82,82 m的区间范围内小于允许最小曲率半径值15 000 m,在此区间范围内,隧道线路平顺性不满足规定要求,影响地铁安全舒适运营,需要在此区间进行重点监控防治。
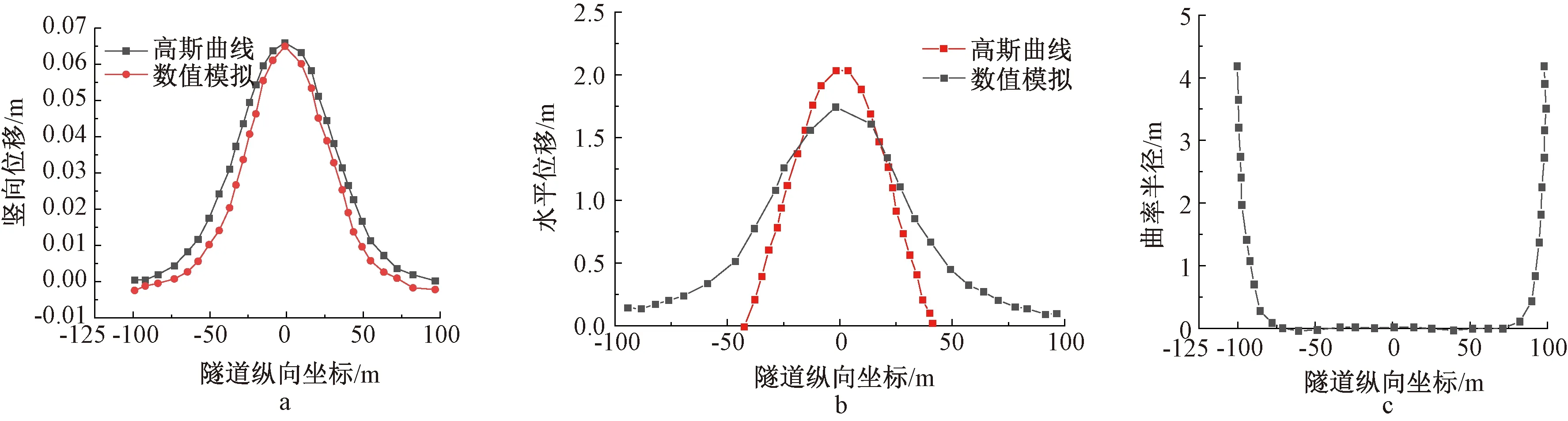
图8 有限元模型数据验证Fig.8 Data verification by the finite element model
从图9可以看出:隧道发生的水平位移由Pasternak模型,Winkler模型计算出的结果分别为4.459,4.463 mm,两者的相差结果不大,Kerr模型计算出的结果为4.451 mm与有限元解相差的最近。这可能是因为在计算过程中,Winkler模型是单因素模型,主要通过土体层参数进行计算,模型的受约束参数比较少,所以得到的计算结果比较大。隧道发生的竖向位移由Pasternak模型,Winkler模型计算出的结果分别为5.464,5.473 mm,Kerr 模型计算出的结果为5.458 mm同样其结果与有限元解相差的最近,Winkler单因素模型的求解结果同样是其中最大的,在该模型中不考虑土层的剪切变形,所需要的参数也相对较少,Kerr模型中需要涉及到三个参数对地基梁刚度矩阵的约束作用比较大,所以得到的计算结果也就相对较小。所以相对来说利用Kerr模型计算出来的结果更加准确,因此可以利用该模型对隧道变形的数值进行计算。
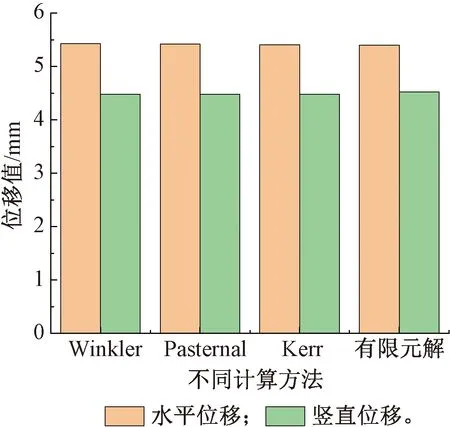
图9 不同计算方法下的位移求解结果分析Fig.9 Calculation results of displacement by different calculation methods
3 结束语
1)在对基坑开挖施工土体卸荷引起隧道变形的计算方法的分析的基础上,研究了基坑施工造成隧道隆起变形的原因,并对基坑开挖过程造成的隆起变形情况进行因素的假设处理。利用差分法对用于求解隧道隆起变形的Pasternak模型,Winkler模型和Kerr模型进行了刚度系数转换, 发现基坑开挖对下卧隧道的附加竖向荷载基本由底部卸荷面产生,而附加水平荷载由五个卸荷面共同作用产生,其中底部卸荷面起主要作用。因此对基坑底面进行加固,可以有效减小基坑开挖对下卧隧道产生的附加荷载。
2)借助有限元分析方法对西安市地铁2号线的实际基坑开挖工程对隧道带来的隆起变形的规律进行了研究,将Pasternak模型,Winkler模型和Kerr模型的计算结果与有限元分析的解进行比较发现Kerr模型的求解结果更加准确。
