基于演化博弈模型的过期药品回收监管策略研究

王培蕊，刘 晨 （江苏大学 管理学院，江苏 镇江 212013）

0 引 言

目前随着我国家庭储备药品数量的不断增加且品种繁多，过期药品的流通和处置已成为学术界和企业界关注的热点问题。过期药品数量的不断增加不仅造成了资源的浪费、环境的破坏，而且给药品使用带来了安全风险。理想情况下，在完全市场经济条件下，资源配置可以通过市场机制自动优化。但在现实中，过期药品的回收受到政策制定、企业成本等诸多动态因素的影响，难以通过市场机制来实现效率的最大化。近年来，随着公众环境保护意识的增长，越来越多的企业开始重视逆向物流，应用在过期药品上指反向供应渠道流动过程以实现过期药品的销毁或回收。由于我国的回收政策有待完善，市场机制不够成熟，政府的监管选择和企业的回收选择正处于一个动态演变的过程。因此，本文从逆向物流的角度，运用演化博弈理论分析如何加强过期药品监管，创新回收模式，以期对我国医药市场的发展有所启示。

1 文献综述

国外已经建立了较为成熟的过期药品回收渠道。Fonara 等引入“局部规范”，研究他人对回收行为的影响。Sushimita 等通过建模研究印度医药行业的逆向物流，并分析了影响行业发展的有效因素。国内的研究者也从不同角度对过期药品的回收利用进行了研究。王智锦认为要联动制药工业、医药电商等多个主体做好过期药品的回收工作。曹允春等从区块链视角构建了过期药品的逆向供应链模型并进行了仿真分析，蒋逸韬等采用问卷访谈法探索我国药品回收的机制。张亚文等通过借鉴发达国家的经验，分析了我国药品回收的背景和现状。

演化博弈论起源于生物演化理论，将博弈分析与动态演化过程相结合，是识别相关影响因素的有用工具。国内学者将演化理论应用于逆向物流的研究，广泛应用于电子、矿业、环保等领域。杜茂康等基于政府、回收企业和市民三主体，构建了废旧家电回收逆向物流博弈模型。付小勇等从政府管制角度出发，针对废旧电子产品处理问题构建了政府与处理商之间的混合博弈模型。方国昌等构建了政企碳减排演化博弈模型。通过对现有文献的梳理发现，大部分研究都围绕我国过期药品回收现状分析并提出建议，利用演化博弈论对过期药品的回收机理进行数值模拟是一个较新的思路，但目前的研究较少。因此，本文试图从这一角度进行深入研究，建立过期药品回收的演化机制，并对政府监管提出建议。

2 模型构建

2.1 问题描述

通过对我国药品回收现状的相关研究，了解到过期药品的回收主要有三种渠道。一是药品管理部门指定专门的站点进行免费回收。例如，在北京、上海等大城市，药品回收箱被放置在指定地点，回收的药品将在有关部门的监督下进行环保处理。二是制药公司有责任回收。例如，中国的一些企业，以广州制药公司和深圳海星制药公司为代表，率先举办了“免费更换家庭过期药品”活动。虽然这些活动很有效，但由于费用高昂，不能定期举行。三是医药零售企业通过一定比例的返款或给予顾客纪念品、优惠券等奖励的方式回收药品。通过这种方式，更多的公众注意力将转移到过期药品的回收问题上。医药零售企业面向全社会，能够灵活多样地回收多种药品。因此，建议过期药品的回收由药品零售企业经营，由政府牵头奖励，由药品管理部门监督。以演化稳定策略和复制因子动力学方程为建模基础，构建了基于政府与药品零售企业演化博弈的药品回收机制。

2.2 模型假设

在市场条件下，该博弈模型包括两组参与者：一组是负责监督回收活动的部门（以下简称政府），另一组是回收者——医药零售企业。在该模型中，政府与药品零售企业每次随机匹配。假设政府的可用策略为A= ｛A,A｝= ｛监督/不监督｝，药店可用策略为B= ｛B,B｝= ｛回收/非回收｝。对政府的假定利益:（1） 缺乏监督。药品零售企业不提供回收过期药品，政府：W 是基本的政府收入，M 是当非法回收过期药品和随意丢弃有害药物时对社会造成的损失。医药零售企业回收过期药品时，对政府的效益为S+T，其中T 为回收产生的社会效益，如健康效益、环境效益等。（2） 存在监督。假设政府对未实施回收的企业的处罚为M；政府的监督成本为D（包括管理成本和宣传成本）。在医药零售企业不实行回收的情况下，给政府带来的好处是S+M-D-W。而如果政府监管是有效的，假设政府在较高水平上分配的资金为Y，政府对实施回收的企业的补贴为Z，那么政府的收益为S+T+Y-D-Z。药品零售企业的假设效益：药品零售企业的基本效益为r。企业在不回收过期药品、不受行政管理部门监管的情况下，将获得基本效益。当他们不回收，但政府监督他们，好处是R-M。当他们选择回收时，政府不监督时，他们的收益是R-C，政府监督时，他们的收益是R+Z-C，其中C 为回收成本。基于上述假设和分析，我们得到收益矩阵，如表1 所示。

表1

演化模型：复制因子动力学实际上是一个动态微分方程，描述了一种策略在一个种群中使用的比例或频率。它反映了玩家的学习速度和方向。基于以上分析，构建了政府与医药零售企业的演化博弈，即RDE（复制因子动力学方程）。假设博弈初始阶段，政府群体选择监管策略的概率为p，而非监管策略的概率为1-p；零售商选择回收过期药品的概率为q，不回收的概率为1-q。

假设政府在监管和不监管时的期望收益分别为U和U，则平均收益为U。

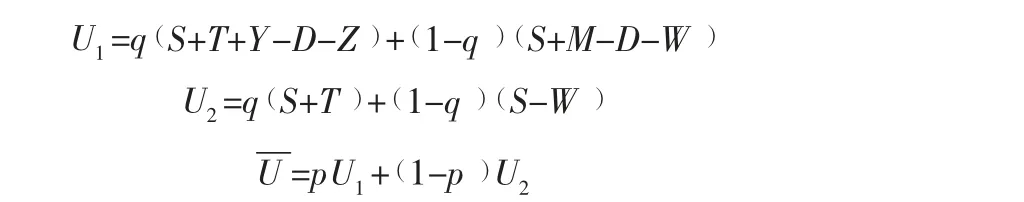
假设零售商回收和不回收时的期望收益分别为V和V，则平均收益为V。

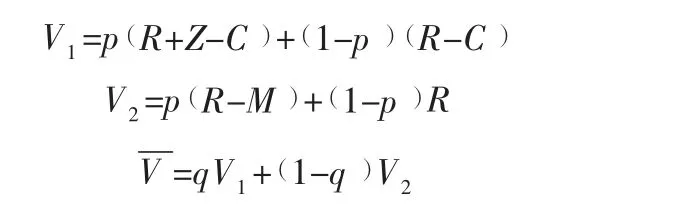
根据马尔萨斯动力学方程，可以知道策略的增长率等于其相应的适应性。那么只要采用这种策略的个体的适应能力高于种群的平均适应能力，这种策略就一定会随着时间的推移而增长。从而得到政府群体与零售商群体之间的演化动态博弈方程。

根据Firedman 的观点，通过分析演化系统雅各布矩阵的局部稳定性，可以得出系统平衡点的稳定性。由上式可知，雅各布矩阵为：

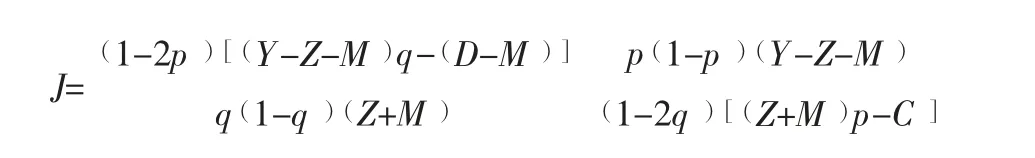
3 稳定性分析

3.1 平衡点及其稳定性分析

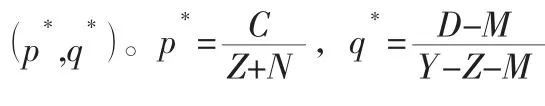
各平衡点的行列式符号和雅各布矩阵的轨迹如表2 所示。

表2

由表2 可以看出，该博弈系统存在（0,0 ）和（1,1 ）两个平衡点，即演化稳定策略ESS。对应的策略是（A,B）和（A,B）。政府与医药零售企业的战略互动如图1 所示。

在图1 中，存在两个非均衡点，N （0,1 ）和H （1,0 ）。连接这些点与鞍点A （p,q）的曲线可以看作是系统收敛到不同模态的临界点。在NAHO 地区的初始状态下，系统将趋同于“无监管无回收”的模式。此模式是一种坏的锁定状态，一旦形成，将不允许出现任何其他模式。在初始状态的NAHL 地区，系统会趋同于“监督与回收”的模式，这是一种理想状态。根据鞍点的表达（p,q），知道鞍点会和因此导致的收敛区域的变化当下列因素变化，包括企业回收过期药品成本，由政府给予补助企业操作循环，政府的监管成本，企业的处罚不执行循环，从政府和基金分配在一个更高的水平。根据这些参数的变化规律，可以提出可行的策略来指导回收工作，以期推动回收工作向良性方向发展。

3.2 多元均衡下的参数分析与调控

图1 政府与药品零售企业行为策略交互过程

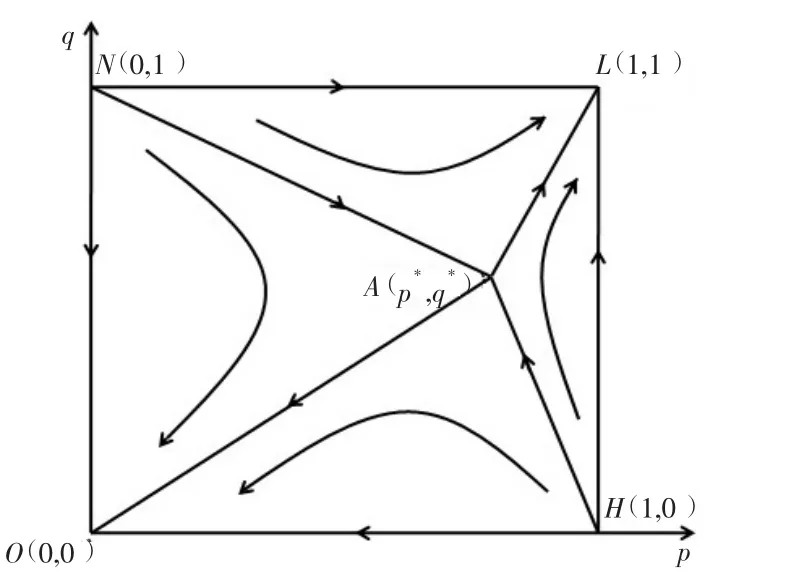
图2 参数C 变化对收敛方向的影响

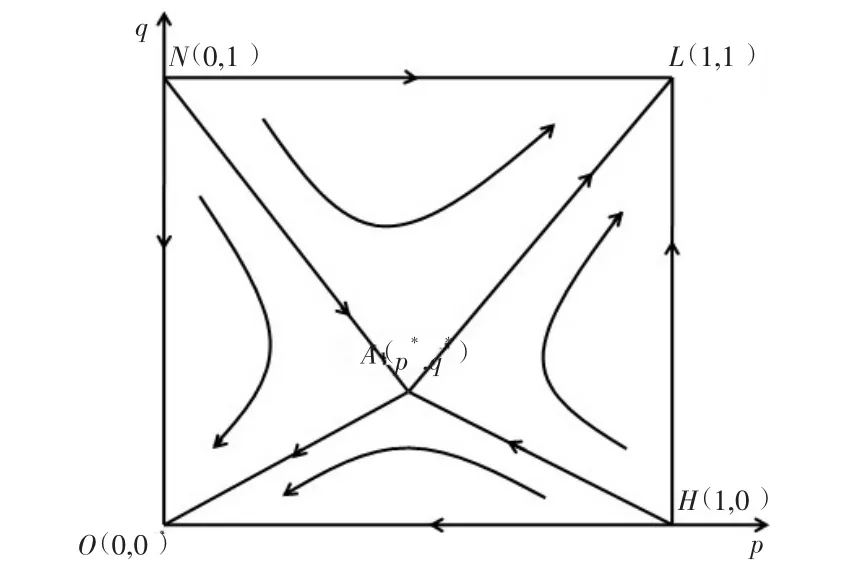
图3 参数Y 变化对收敛方向的影响

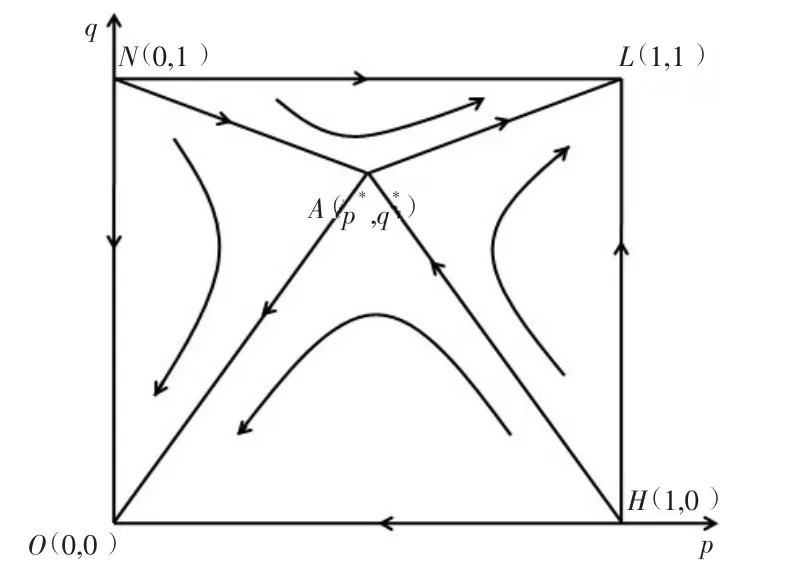
图4 参数D 变化对收敛方向的影响

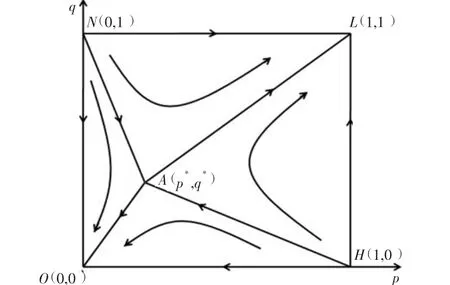
图5 参数M 变化对收敛方向的影响

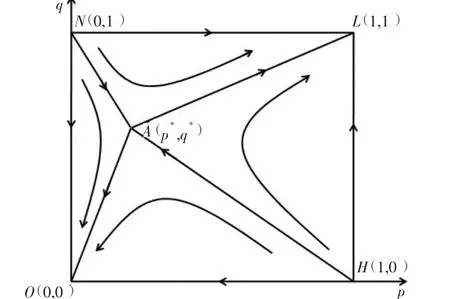
图6 参数Z 变化对收敛方向的影响

3.3 数值模拟与结果分析

基于动力学方程描述的演化策略采用政府和药品零售企业随着时间的推移，使用Matlab 软件演化过程的数值模拟，分析以下因素对演化的影响，包括个人使用某些策略的比例，政府在企业实施的惩罚，没有实现回收过期药品，上级政府的奖励分配、企业的回收成本、政府的监督成本等。

（1） 使用某种策略的个体比例对演化的影响。仿真结果如图7 所示，其中p和q分别代表政府采取“监管”策略的初始比例和个人选择“回收”策略的比例。D=0.4，M=0.2，Z=0.3，C=0.45，Y=0.8。参数的取值严格符合约束条件。从图7（a） 和图7（b） 可以看出，不同初始条件下出发的轨迹在收敛达到平衡状态之前会发生重叠。p的收敛方向和速度与q的收敛方向和速度有关。q越大，p收敛到理想模式的可能性越大，收敛速度越快。研究表明，政府人口的演化不仅受选择监管的初始人口比例的影响，还受选择实施回收的初始企业比例的影响。

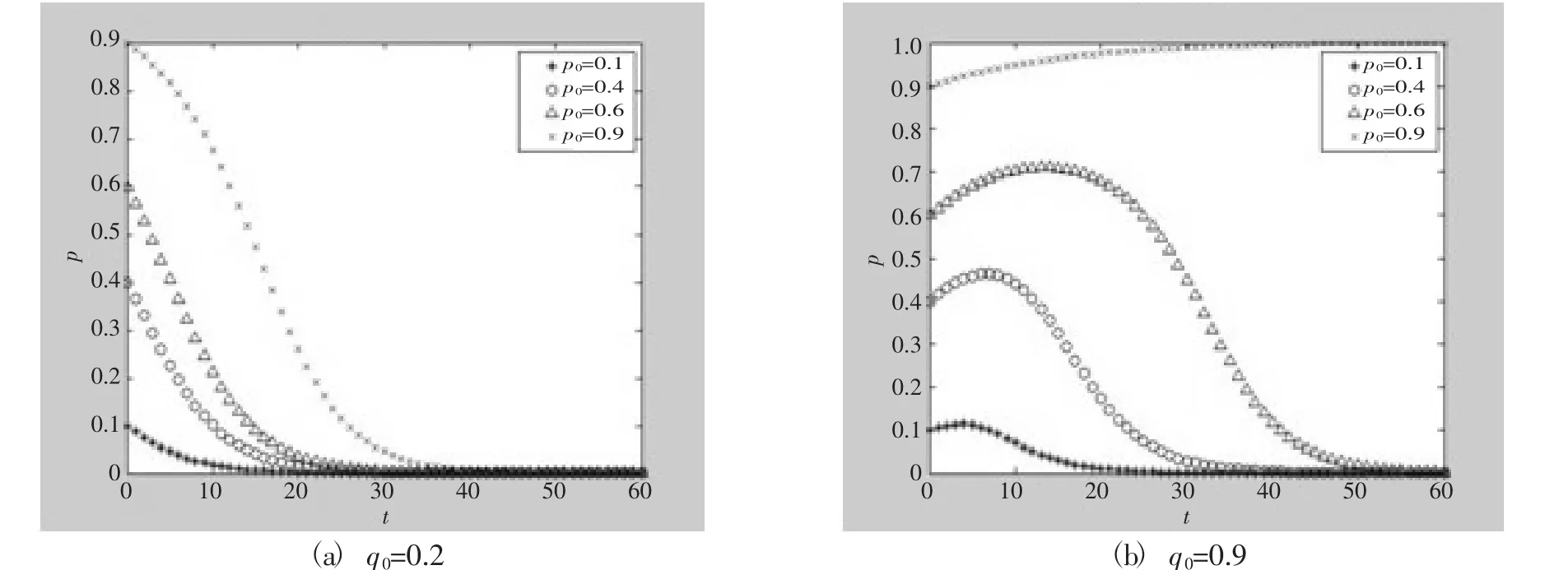
图7 选择一种策略的种群初始比例对演化的影响

（2） 政府的处罚对没有回收的企业的影响。在q=0.5，M=0.18，M=0.38 的初始比例下，保持其他参数不变，仿真结果如图8 所示。对比图8（a） 和图8（b） 可以发现，当M=0.18 时，四条轨迹都收敛到一种模式，而当M=0.38 时，两条轨迹收敛到理想状态，另外两条仍然收敛到病态状态，但收敛速度明显较慢。这说明当企业因不实施回收而受到严厉惩罚时，他们就会在下一轮博弈中采取回收行动，从而削弱了回收的阻力。这证明，对不愿实施回收的企业加大惩罚力度，可以极大地推动企业向理想状态演化。

图8 政府对不愿回收的企业的处罚对演化的影响

（3） 在政府监管有效的情况下，政府在更高层次上分配资金的变化对演进的影响。在q=0.5 的初始比例下，令Y=1，Y=2 等参数不变。仿真结果如图9 所示。对比图9（a） 和图9（b），发现当政府分配少量资金时，往往不进行监督，使得系统朝着（A,B）的方向发展。随着Y 增加，政府将演化的一部分（A,B），当政府发现，其有效监督将使企业变得更加合作，赢得政府的赞扬和奖励在更高的层面，将提高工作效率和完善监管流程，赢得更多的支持，政府工作上升到一个更高的水平。因此，更高层次的政府支持，必将推动过期药品的回收利用。

图9 在更高层次上政府所分配资金的变化对演变的影响

（4） 企业回收过期药品的成本对演化的影响。在q=0.5 的初始比例下，令C=0.4，C=0.05 等参数不变。仿真结果如图10所示。当企业在回收药品上投入大量资金时，三条轨道就会聚到“无监管、无回收”的病态“锁定状态”；当成本下降时，三条轨道会汇聚到“监管回收”的理想状态。因此，可以得出，降低企业回收药品的成本对过期药品的回收将产生积极的影响。

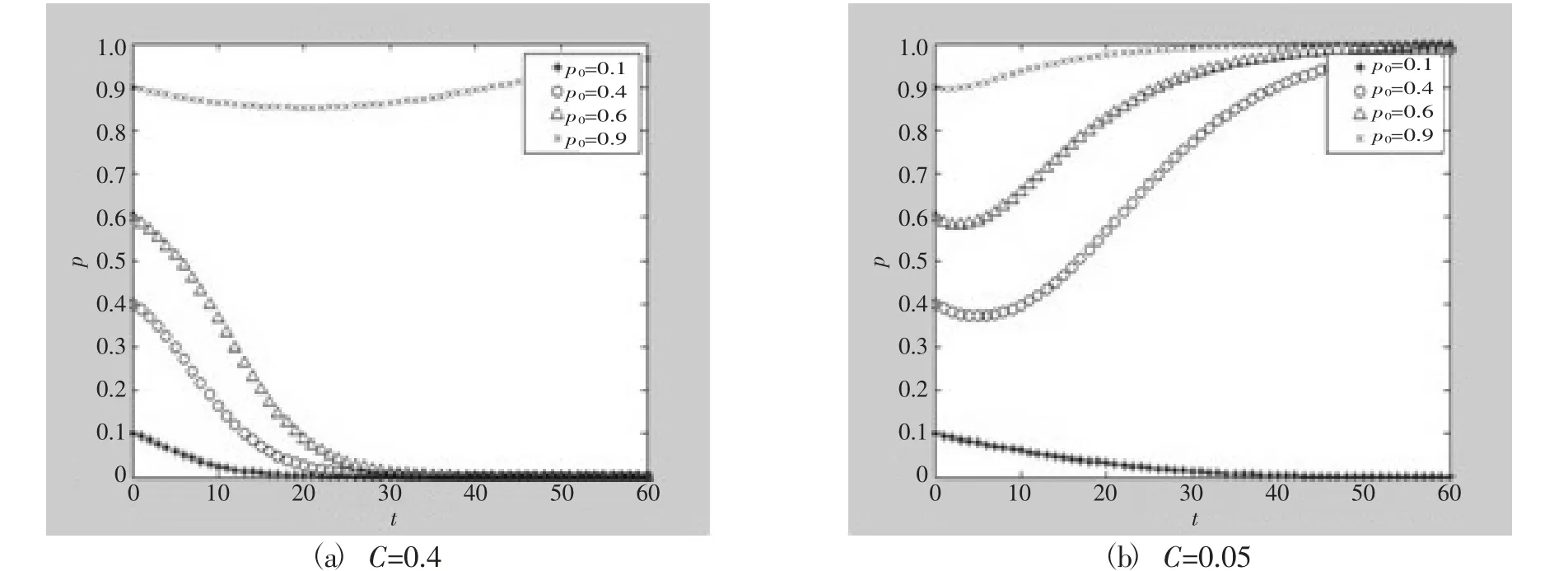
图10 企业过期药品回收成本变化对演进的影响

（5） 讨论政府监管成本的变化对演进的影响。仿真结果如图11 所示。假设选择实施回收的企业人口比例仍为0.5，其他参数不变，则政府的监管成本分别为D=0.22 和D=0.48。由图11 可以看出，当成本相对较低时，两条轨迹收敛为两种模式；而当成本较高时，两条轨道会聚到“无监管、无回收”的病态“锁定状态”。因此，降低政府的监管成本也会推动过期药品的回收向理想状态发展。

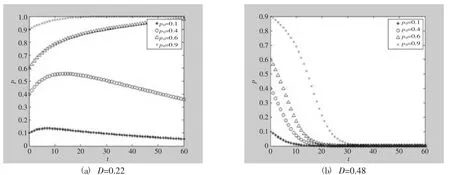
图11 政府监管成本变化对演进的影响

4 结 论

本文建立了回收过期药品中寻租行为的演化博弈模型。在模型中导出了两种演化稳定策略：一种是“监督与回收”的理想均衡状态，另一种是“无监督无回收”的病态“锁定状态”。从数值模拟的结果可知，演化受到政府群体、医药零售企业所采取的策略、企业实施回收成本和相关制度的影响。因此，建议政府应尽一切可能建立健康、全面的过期药品回收机制。本文对管理的启示在于以下几点：

（1） 建立有效的法律制度，规范过期药品的回收利用。借鉴国外立法的经验，考虑我国的现实，通过法律规定政府、企业和公众指定义务。

（2） 明确有关部门的监督管理职责。在回收过程开始前，药品监督管理部门应当对回收计划进行效率分析，在回收过程后，加强有关部门和本部门对回收药品的处置和流动的监督管理。

（3） 政府要努力降低监管成本，完善过期药品回收奖惩制度设计。政府应当认真制定从回收到过期药品处置、销毁的各个环节的标准，避免不必要的管理成本，对执行过期药品的企业给予适当补贴。

（4） 在指定药店设计免费回收模式。考虑不同地区发展水平和基础设施差异，政府应制定合理的负责回收的药店分布图，将专业回收与宣传活动相结合，以期完善家庭过期药品的回收机制。