飞机液压系统出油管路振动抑制方法研究

邵敏强，张胜发，杨乐，黄自力

1.南京航空航天大学机械结构力学及控制国家重点实验室，江苏 南京 210016

2.航空工业金城南京机电液压工程研究中心航空机电系统综合航空科技重点实验室江苏 南京 210001

飞机液压系统是飞机控制、起落架收放、导弹发射等负载的动力源，而液压管路主要承担着液压油的输送，整个液压系统的安全性对于飞机正常飞行有着关键的作用，我国飞机目前普遍采用的压力体制为21MPa，下一步目标是提升到35MPa压力级别，与国际先进客机接轨，因此对高压系统的研制需求极为迫切。但是，飞机液压系统在进行高压化的过程中也带来了一系列的技术难题，其中液压管路振动加剧导致的安全问题尤为严重，而管路流固耦合作用导致的复杂振动更是对民机液压系统的设计提出更严峻的挑战，也是迫切需要解决的问题。

液压管路不仅包含流体泵脉动引起的振动，而且涉及主体结构传递至管路的振动，采用增加卡箍约束的方法往往难以达到理想的振动抑制效果。有必要采用其他方法对其进行振动抑制研究。2005 年，张偕锋等[1]用压电片作为驱动器，对两端固支的液压管路进行振动控制，取得了很好的控制效果。2007 年，欧阳平超等[2]采用前馈控制和多通道自适应滤波算法对飞机液压管路进行振动控制，使消振器产生的次级脉动与管路脉动相互抵消，结果表明，此方法抑振效果可达10dB以上。2011年，李鑫[3]针对管系的振动问题设计了可拆分的环形调谐质量阻尼器，研究结果表明调谐质量阻尼器可以使管系的振动幅值快速大幅度衰减，有着良好的振动抑制效果。2015 年，徐鉴[4]提出了一种时滞反馈减振技术，通过主动控制方法降低管路振动，提高管路的临界流速，优化了输流管路的性能。T.Chiba 等[5]先是研究了如何控制悬臂输流管路的颤振，并分析了控制器质量位置对于管道的稳定性和其控制性能的影响。之后，T.Chiba[6]又针对悬臂管路的振动设计了PID 控制器和H 控制器。

半主动振动控制是通过实时调整振动控制器的刚度或阻尼，实现宽频范围内振动能的瞬时存储和耗散。半主动振动控制既具有被动振动控制的可靠性，又具有主动振动控制的强适应性。2010 年，哈尔滨工程大学高林等[7]针对水管路中噪声频率的复杂变化特点，设计了一种半主动的水管路脉动压力消声器，取得较好的消声和调频效果。陈果[8]等设计了一种装在管路上的弹簧式动力吸振器，此吸振器由最简单的弹簧片-质量块组成，具有结构简单、调频方便等优点，通过试验表明，此吸振器能将共振频率降低90%以上。

1 基于ANSYS的有限元分析

1.1 飞机液压管路模型及网格划分

根据实际飞机液压管路系统，针对管路系统振动明显的位置进行测绘，获得管路局部几何参数，具体模型如图1所示。整个管路段涉及7处弯折，入油口与软管相连，管路上有三个卡箍。管道材料为21-6-9 不锈钢，其中管道外径为25.4mm，壁厚为1.32mm，管道的密度为7750kg/m3，弹性模量为1.9×1011Pa，泊松比为0.31；系统使用Skydrol LD-4液压油（密度1.006g/cm3，运动黏度139mm/s，动力黏度0.14），介质声速为1400m/s。

图1 空间管路的三维模型Fig.1 Three-dimensional model of space pipe

管路系统根据管道和内部流体分为固体域和流体域，分别采用不同的网格划分方式进行有限元建模，管道在Mechanical中进行网格划分，内部流体Fluent中进行网格划分，分别采用四面体和六面体单元，具体结果如图2所示。

图2 管路与管路内流体部分网格划分Fig.2 Meshing of pipe and fluid part in pipe

1.2 液压管路动态特性

运用ANSYS Workbench 软件中对管道系统进行流固耦合分析，在Fluent中求解流场，并将Fluent的运算结果以载荷的形式导入Static Structural 中求解，然后通过model 模块提取管道的固有频率，分析不同条件下管道的固有频率变化。

保持入口的压力不变，改变管道入口速度，分析在不同流体流速下管道的固有频率变化，表1 为管道入口流体流速分别为0、1、2、3和4m/s时的前2阶固有频率。

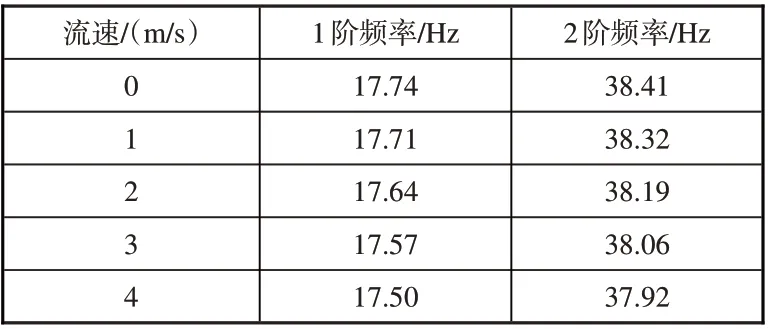
表1 液压管道在不同流体流速下的固有频率Table 1 Natural frequency of hydraulic pipe at different flow rates

保持入口的速度不变，改变管道入口压力，分析在不同流体压力下管道的固有频率变化，表2 为管道入口流体压力分别在0、10MPa、20MPa和30MPa时的前2阶固有频率。

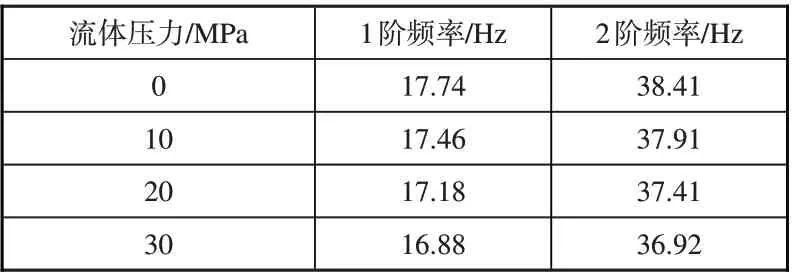
表2 液压管道在不同流体压力下的固有频率Table 2 Natural frequency of hydraulic pipe under different fluid pressure

流固耦合作用对液压管道的固有频率有着较大的影响，含液管道的各阶固有频率都要比空管的固有频率偏低。表1反映了管道内流体流速会引起液压管道系统固有频率的变化，液体流速从静止到4m/s 逐级增加，前两阶固有频率均呈下降趋势，其中一阶固有频率从17.74Hz 下降至17.5Hz，下降1.35%；表2 反映了管道内流体压力的改变也会引起液压管道系统固有频率的变化，当流体压力从0 增加到30MPa，前两阶固有频率均呈下降趋势，其中1阶固有频率从17.74Hz下降至16.88Hz，下降了4.8%。

1.3 液压管路瞬态响应分析

用ANSYS Workbench对管路进行瞬态分析，采用弹性支撑来模拟管路上的卡箍约束，入口速度由液压泵的出口流量决定，本次仿真所选用的液压泵为恒压变量泵，流量为130L/min，稳态工作时流体压力为21MPa，选取1 阶模态共振时管道位移最大的一点作为观测点,如图3所示。

图3 选择位移最大时的特征点Fig.3 Distribution of peak electron number densities along axial flow field

已知液压泵的脉动率为6%，通过公式v=Q/A计算其入口速度为v= 2.97 + 0.18 sin(2 ⋅f⋅π ⋅t)，单位为m/s，f为脉动的频率。分别对管道共振时和非共振时两个工况的仿真结果进行分析。工况1：入口速度的脉动频率取17Hz，此时系统处于共振状态；工况2：入口速度的脉动频率取10Hz，此时系统处于非共振状态。其响应结果如图4、图5所示。

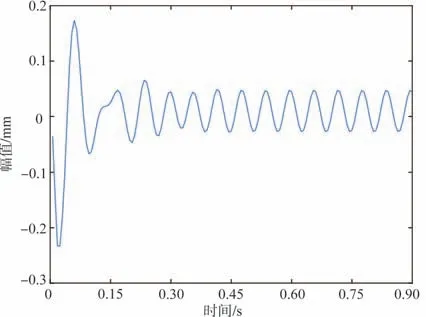
图4 工况1特征点y方向位移响应Fig.4 Displacement response of feature point in y direction under condition 1

图5 工况2特征点y方向位移响应Fig.5 Displacement response of feature point in y direction under condition 2

图4和图5的振动响应表明，液压管道在脉动流体激励下，初始时刻会经历幅值较大的瞬态过程，然后进入稳定振动阶段，在工况1 中，系统处于共振状态，其稳态振动位移幅值为0.035mm；在工况2 中，我们使脉动频率远离系统固有频率，此时系统处于非共振状态，其稳态振动位移幅值为0.009mm，比工况1中大幅度减小。

2 液压管路半主动控制方法

2.1 半主动吸振装置

2.1.1 半主动吸振器吸振机理

动力吸振器的原理是在振动物体上附加质量弹簧共振系统，利用质量弹簧系统在共振时吸收物体的振动能量以减少被控物体的振动。将加装了吸振器的管路段简化为如图6所示的两自由度系统。

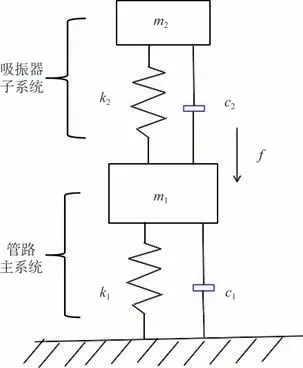
图6 管路-半主动吸振器简化模型Fig.6 Simplified model of pipe-semi-active vibration absorber

根据简化模型，写出系统的振动方程

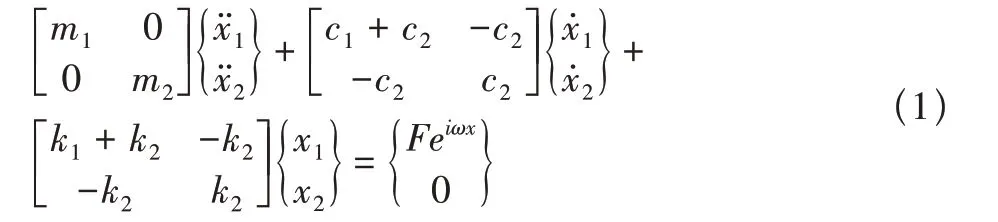
经过计算和变形得主系统的动力放大系数

其中

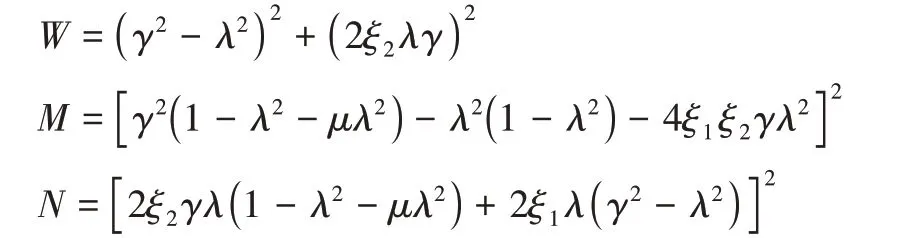
γ=ωn2/ωn1表示吸振器与主系统的固有频率比值，λ=ω/ωn1表示激振力与主系统的频率比值，μ=m2/m1表示吸振 器 与 主 系 统 之 间 的 质 量 比。ξ1=c1/2m1ωn1、ξ2=c2/2m2ωn2分别表示主系统和吸振器的阻尼比，ωn1=，ωn2=分别表示主系统和吸振器的固有频率。

当k2保持不变时，吸振器的固有频率保持不变，此系统为被动式吸振系统。由式（2）可以看出，当吸振器的固有频率与激励频率相等时，γ2−λ2=0，此时主系统的振幅比会非常小，若是忽略吸振器的阻尼c2，此时主系统的振动幅值为0。而半主吸振器则是需要根据激振频率改变自己的固有频率，是自己时刻保持这种共振状态，从而降低主系统的振动幅值。

分别讨论不安装吸振器、安装被动式动力吸振器以及安装半主动动力吸振器三种情况，根据式（2）通过Matlab求解三种工况下主系统的动力放大系数。

由图7可以看出，被动式吸振器的在其固有频率和外激励频率r比值接近1时，会有很好的吸振器效果，但是在固有频率的附近会出现两个新的共振峰，这种动力学特性可能会使得主系统的振动更加复杂。而半主动吸振器相当于若干被动式吸振器组合在一起，可以随时匹配外激励频率，半主动吸振器在作用频带范围内都有着很好的振动控制效果。

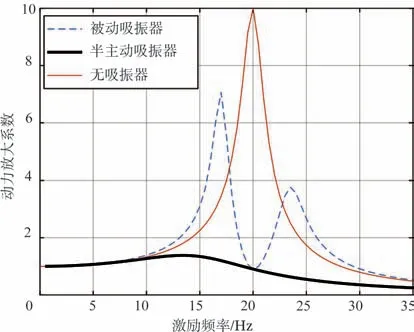
图7 安装不同吸振器时系统的频率响应Fig.7 Frequency response of the system when different vibration absorbers are installed

2.1.2 吸振器设计

根据液压管路的振动特性，设计如图8所示的吸振器，它主要由弹性元件与吸能质量块组成，弹性元件为一根上下表面都贴着压电薄膜的H 梁。悬臂梁的主体材料为钢，弹性模量为210GPa，密度为7800kg/m3。质量块质量设置为0.2kg。当给压电薄膜通电时，它会产生轴向的力，借此来改变梁的刚度，从而改变吸振器的固有频率。

图8 H形悬臂梁吸振器有限元模型Fig.8 Finite element model of H-cantilever vibration absorber

按照给定的参数进行有限元仿真，将压电片的电压变化范围设置在0～1500V，得到吸振器在不同电压作用下的吸振器的频率。此吸振器的固有频率随电压变化如图9所示，其变化范围为14～19Hz。

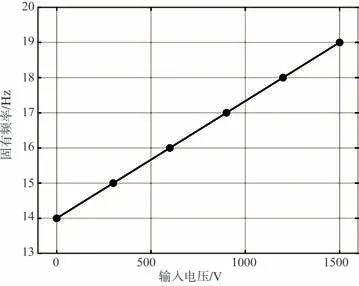
图9 不同电压下吸振器的固有频率仿真结果Fig.9 Simulation results of natural frequency of vibration absorber under different voltages

2.2 逐步寻优算法

逐步寻优算法根据最优路线的决策集合对于初始值和终止值都是最优的这一特性，将问题分解为多个2 阶段问题，每次都只对多阶段决策中的两个决策进行优化调整，将上次优化结果作为下次优化的初始条件，如此逐时段进行，反复循环，直至收敛。

通过逐步寻优算法调节吸振器固有频率，使其与液压管路的振动频率达到一致，实现有限频带范围内的最佳吸振效果，算法控制流程如图10所示。

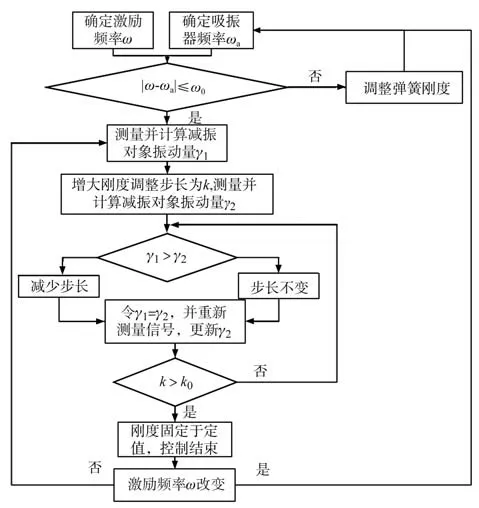
图10 逐步寻优算法控制流程Fig.10 Flow chart of progressive optimization algorithm

控制过程主要分为两步：（1）识别激振频率并将吸振器固有频率调整至激振频率附近；（2）寻优过程，调整吸振器的固有频率使减振对象的振动降到最低。

2.3 粒子群优化算法

粒子群算法是由Kennedy 和Eberhart 博士通过观察鸟类觅食行为而提出的一种基于群体智能的全局搜索算法。他们设想了一个场景：一群鸟正在寻找食物，假设某一区域只有一种食物，所有鸟类都不知道食物在哪里，但知道食物离自己有多远，最好的办法是先找到鸟类周围离食物最近的区域，然后通过信息更新和迭代确定食物的位置。

Eberhart 博士从该模型中得到启示，用粒子来代入鸟群，首先初始化一组随机粒子，在粒子中挑出两个极值，然后其他粒子将围绕极值更新。在每次新的迭代之后，重新更新极值，然后通过多次迭代找到最优解。

将粒子群算法用作半主动吸振器的控制算法，把吸振器的固有频率当成是粒子，而固有频率对应的振动响应幅值当成是适合度，其实现的主要流程如图11所示。

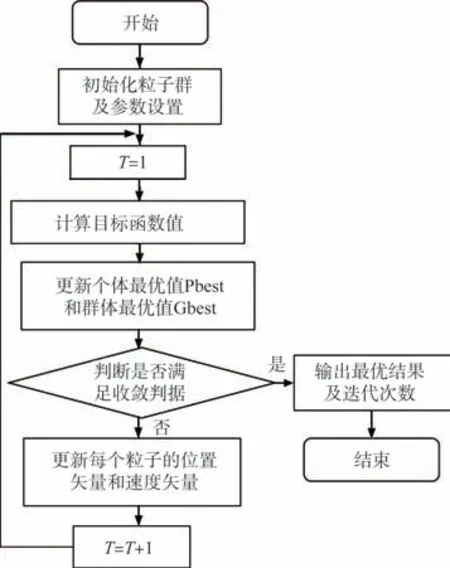
图11 吸振器粒子群算法流程Fig.11 Flow chart of particle swarm optimization for vibration absorber

具体过程如下：（1）初始化一组吸振器固有频率值；（2）计算每个固有频率值粒子对应的振动量γ；（3）根据振动量选择每个粒子个体的历史最佳频率；（4）根据振动量选择每个粒子个体的历史最佳频率；（5）根据步长和频率计算公式更新粒子的频率值和步长；（6）判断是否满足结束条件，则转至步骤（2）。

2.4 复杂模型的振动控制联合仿真方法

由于控制算法需要实时调整吸振器的固有频率，难以直接采用有限元软件实现系统控制的数值仿真，结合Python和ABAQUS联合仿真进行数据交互，实现受控系统的动力学响应计算，能够有效解决复杂模型的振动控制数值仿真问题。具体联合仿真流程如图12所示。

图12 Python-ABAQUS联合控制仿真流程Fig.12 Python-ABAQUS joint control simulation flowchart

整个仿真的过程主要分以下几个步骤：（1）通过ABAQUS创建模型，建立某一工况，并导出inp文件；（2）Python读取inp文件和位移响应；（3）通过控制算法修改inp 文件里面的关键字，使得激振频率逐步增大，吸振器的固有频率与激振频率相近，并通过寻优使得主系统的振动频率降到最低。

3 半主动控制仿真及结果分析

采取在液压管路1阶模态位移最大值处设置半主动吸振器，如图13所示，动力振子质量为0.2kg，频率可调范围为14～19Hz，采用逐步寻优算法自动调节吸振器固有频率。将该点作为振动量观测点评价振动效果，ABAQUS求解系统的响应，分析吸振器的减振效果。

图13 液压管路-吸振器有限元模型Fig.13 Finite element model of hydraulic pipe-vibration absorber

液压管路的一阶固有频率为17Hz，由于流固耦合作用，主系统的固有频率会在一定范围内变化，设置简谐激励频率范围为14～44Hz，频率间隔为0.1Hz，分别求解不加吸振器和加半主动吸振器时的系统响应。

同时分析液压管路在有无吸振器时的振动响应，仿真效果如图14所示，图中的曲线分别表示装吸振器和不装吸振器时的系统响应，可以看出，在14～19Hz范围内半主动吸振器都有很好的吸振器效果，但是超出频带范围，接近第2阶共振频率时，又会出现新的共振峰。因此我们可以考虑同时用两个不同频带范围的半主动吸振器来达到更佳的吸振效果，如图15所示。同时在一阶模态位移最大值处和二阶模态位移最大值处施加吸振器，采用逐步寻优控制算法，获得多个吸振器作用下的结构响应，如图16所示。

图14 吸振器控制前后比较Fig.14 Comparison before and after vibrator control

图15 液压管路-双吸振器有限元模型Fig.15 Finite element model of hydraulic pipe-double vibration absorber

图16 双吸振器控制前后比较Fig.16 Comparison before and after dual vibration absorber control

由图16 可以看出，在管路上安装两个吸振器时，第1、第2 阶模态的共振峰都得到了抑制，在14～44Hz 范围内都有很好的吸振效果。

对于图15中的液压管路系统，用粒子群算法控制半主动吸振器，求取响应并与逐步算法结果进行比较，其结果如图17所示，在整个频域上粒子群算法于逐步寻优算法的控制效果比较接近。

图17 两种控制算法的控制效果比较Fig.17 Comparison of control effects between two control algorithms

4 结论

本文先对实际的液压管路进行了有限元仿真，得到了液压管路的振动特性，然后根据其振动特性采用刚度自调谐吸振器结合半主动控制算法对管路进行振动控制研究，主要结论如下：

（1）结合ANSYS 仿真平台建立航空液压管路流固耦合系统模型，获得不同流速和压力情况下管路系统的动力学特性，研究结果表明，管道的固有频率会随着管道内流体流速的增加而减小，随着管内压力的增加而减小。

（2）结合Python 和ABAQUS 建立复杂管路模型联合动力学仿真方法，验证液压管路在多个吸振器作用下的半主动控制效果。结果表明，吸振器能够同时对液压管路系统前两阶模态振动进行有效抑制，振动衰减可达45dB 以上。