改进的准定常旋转坐标系阻尼动导数计算方法

2022-07-30吴耕宇鲍君波宋万强相倩

航空科学技术 2022年7期

吴耕宇，鲍君波，宋万强，相倩

中国航空研究院，北京 100012

飞行器动导数是飞行器姿态控制系统设计、弹道设计及动态稳定性分析中的关键参数[1-2]，在高超声速飞行器[3]、可重复使用的跨大气层轨道飞行器[4]等各类先进飞行器的动态稳定性分析中具有重要作用。计算流体力学（CFD）技术目前已广泛应用于动导数的计算。使用CFD 技术计算动导数主要有准定常和非定常两种方法，准定常方法一般通过模拟定常拉升或匀速滚转运动计算俯仰、滚转、偏航阻尼动导数，非定常方法一般通过模拟强迫振荡等方法计算气动力系数相对于俯仰角速度和迎角变化率的组合、气动力系数相对于偏航角速度和侧滑角变化率的组合等组合动导数。国内外已有多位学者使用CFD 方法进行动导数计算的研究。S.M.urman等[5]采用减缩频率方法对基本尾翼导弹（BFM）、改进的基本尾翼导弹（MBFM）和标准动力模型（SDM）三个标模进行动导数计算；Le Roy 等[6]对稳定性和控制构型（SACCON）翼身融合体布局进行了静导数和动导数的CFD计算和分析；Da Ronch等[7]使用Euler方程和雷诺时均纳维-斯托克斯（RANS）方程分别对SDM 标模和跨声速巡航标模（TCR）进行了非定常动导数的计算，并进行了较为详细的分析；袁先旭等[8]使用时空二阶精度的隐式迭代无波动、无自由参数的耗散差分（NND）算法对尖锥、钝锥、弹道外形和飞船返回舱等典型再入飞行器进行了俯仰静、动导数的计算；范晶晶等[9]采用逐次超松弛时间推进方法耦合求解非定常纳维-斯托克斯（N-S）方程和强迫运动方程，对美国国家航空咨询委员会（NACA）开发的标准翼型（NACA0012）、弹道外形和有翼导弹等飞行器进行了强迫俯仰振荡的黏性动态流场求解；叶川等[10]分别采用基于强迫振荡的非定常方法和基于定常拉升的准定常旋转坐标系方法计算BFM 模型和水上飞机模型的组合动导数和阻尼动导数，该方法计算机体坐标系下非零迎角滚转阻尼动导数需要在计算稳定坐标系下滚转阻尼动导数和交叉动导数的同时计算稳定坐标系下偏航阻尼动导数和交叉动导数；米百刚等[11]通过强迫振荡方法和基于圆环网格的定常拉升方法辨识单独动导数，并采用BFM 模型进行验证；张一帆等[12]对欧洲动导数标模（DLR-F12）标准模型进行非定常强迫振荡和准定常旋转坐标系方法，获得良好的组合动导数和阻尼动导数结果；相倩等[13]计算了BFM模型大迎角状态下的非定常动导数，反映了流场非线性特征；朱海涛等[14]使用非定常强迫振荡计算方法对TCR 标模进行了动导数计算的详细研究；宋万强等[15]采用在物面处添加法向扰动速度模拟强迫振荡的方法计算DLR-F12 标模的动导数，实现无网格变形的非定常动导数计算。非零迎角下的滚转阻尼动导数计算是动导数计算的一种特殊情况，国内外对于该情况具有一定程度的研究，但相比俯仰阻尼动导数的计算研究较少。叶川等[16]利用涡格法和理论推导得到的动导数计算公式计算临近空间长航时太阳能飞行器的非零迎角下的滚转阻尼动导数，并研究总体气动参数对动导数的影响机理；岳杰顺等[17]、王纪林等[18]采用多参考系方法计算非零迎角下的滚转阻尼动导数，将计算网格分为旋转网格和固定网格两部分，模型附近为旋转网格，模型绕纵轴旋转，这种方法主要应用在弹箭等较为接近圆柱体构型的滚转动导数计算，对于飞机构型来说，飞机旋转90°时，迎角将变为侧滑角，该方法无法正确模拟；V.A.Bhagwandin[19]采用模型整体以恒定角速度旋转的非定常方法计算了BFM和MBFM标模在-5°～90°迎角下的滚转阻尼动导数等多个气动导数，并与试验值进行对比；刘伟等[20]采用基于简谐振动的非定常方法计算非零迎角下的动导数，辨识得到滚转组合动导数；B.Etkin[21]提出计算机体坐标系下非零迎角滚转阻尼动导数可通过计算稳定坐标系下滚转阻尼动导数和交叉动导数，同时计算稳定坐标系下偏航阻尼动导数和交叉动导数求得，参考文献[10]提及了该方法，计算了稳定坐标系下非零迎角滚转阻尼动导数，并与机体坐标系下的试验结果进行对比。

本文通过将来流速度分解的处理手段将基于旋转坐标系的准定常CFD 动导数计算方法[10]进行改进。通过将速度矢量分解为垂直于旋转轴和平行于旋转轴两个分量，以垂直于旋转轴的速度分量计算旋转半径并推算参考坐标系的旋转中心点，以平行于旋转轴的速度分量作为来流速度矢量计算气动力系数，通过计算两个不同角速度的气动力系数之差求得动导数。使用欧洲动导数标准模型（DLRF12）和跨声速巡航标模（TCR）进行滚转、俯仰和偏航动导数计算，并与风洞试验数据、参考文献[10]的准定常计算方法和参考文献[22]提供的其他CFD 计算结果进行对比，以对改进方法进行验证。

1 计算方法

现有的基于旋转参考坐标系的准定常阻尼动导数计算[10,12]一般通过模拟定常拉升/定常绕轴旋转或者模拟旋转轴与来流方向平行的旋转运动两种途径获得。定常拉升如图1所示，飞行器绕飞行器上方的旋转轴以固定角速度q旋转，旋转半径为R，来流速度为0，此时飞行器的运动速度大小为

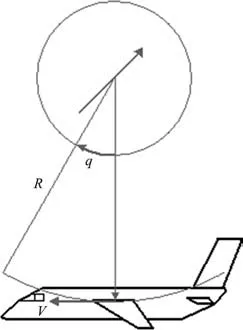
图1 飞行器定常拉升Fig.1 Aircraft steady state lifting

在相对飞行器固定的机体坐标系下，定常拉升运动时飞行器的运动速度大小和方向、旋转角速度大小和方向、迎角和侧滑角均保持不变，因此可用准定常方法进行动导数计算。取不同的角速度q1和q2分别计算相应的气动力或力矩系数Ci1和Ci2，其中Ci为升力系数CL、俯仰力矩系数Cm或其他气动力或力矩系数，则相应的动导数Ciq可由式（2）计算[12]

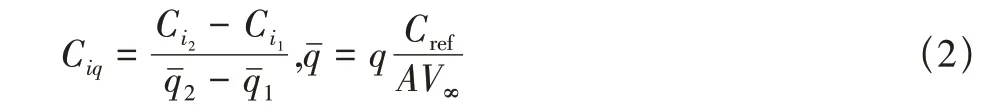
式中：Cref根据所计算动导数的不同，为纵向参考长度或参考展长，V∞为来流速度，A一般取2，部分计算模型为与风洞试验处理一致取1[12]。定常绕轴旋转选取飞机左侧或右侧的旋转轴，飞机绕旋转轴定常运动，来流速度为0，动导数的计算方法与定常拉升类似，通过计算两个不同旋转角速度的气动力系数，通过式（2）求得动导数，通常用于计算偏航阻尼动导数。旋转轴与来流方向平行的旋转运动，在机体坐标系下，飞行器运动速度大小和方向、旋转角速度大小和方向、迎角和侧滑角均保持不变，也可使用基于旋转坐标系的准定常方法计算，通过计算两个不同旋转角速度的气动力系数，通过式（2）求得动导数。

模拟定常拉升/定常绕轴旋转或者模拟旋转轴与来流方向平行的旋转运动两种处理途径只能计算部分情况的阻尼动导数。一种典型的无法使用上述两种处理途径直接计算的情况是计算非零迎角下的滚转阻尼动导数。参考文献[10]中计算非零迎角下的滚转阻尼动导数需要通过模拟旋转轴与来流方向平行的旋转运动途径计算稳定坐标系下滚转阻尼动导数和交叉动导数，并通过模拟定常拉升/定常绕轴旋转运动途径计算稳定坐标系下偏航阻尼动导数和交叉动导数。稳定坐标系下的滚转运动、稳定坐标系下的偏航运动和机体坐标系下的滚转运动分别如图2～图4 所示。计算完成后，采用式（3）[10,21]进行机体坐标系下动导数的求解。

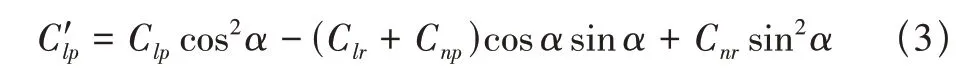
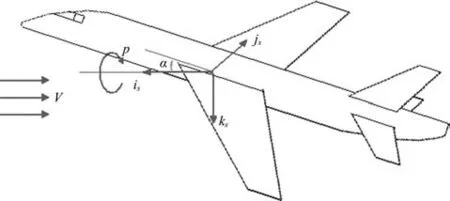
图2 在稳定坐标系中匀速滚转Fig.2 Rolling in stability coordinate frame

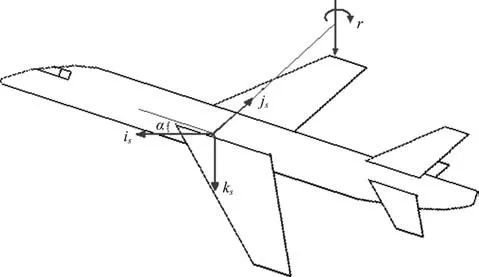
图3 在稳定坐标系中绕轴偏航Fig.3 Yawing in stability coordinate frame

图4 在机体坐标系中匀速滚转Fig.4 Rolling in body coordinate frame

1.1 非零迎角下的滚转阻尼动导数计算

假设迎角不为0，侧滑角为0，将飞机相对于地面运动速度矢量V分解为平行于机体坐标系x轴方向Vx和垂直于机体坐标系x轴方向Vz两个分量。假定初始状态风轴系和地面坐标系的坐标轴平行，则俯仰角和迎角相同，且飞机沿地面坐标系x轴运动，由于迎角为飞机体轴系和风轴系的夹角，如图5所示，有

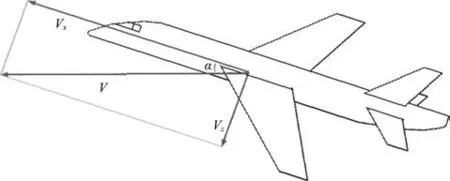
图5 飞机运动速度矢量分解示意图Fig.5 Aircraft velocity vector decomposition map

式中：α为迎角，ib，kb分别代表机体坐标系的单位矢量。考虑一个较小的单位时间Δt，在Δt时间内，飞机运动距离为|VΔt|i，i代表地面坐标系x方向的单位矢量。记ω为飞机旋转角速度，则飞机旋转角度为ωΔt，下一个Δt时间，飞机运动距离则为

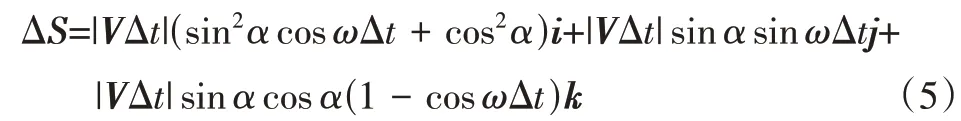
式中：i，j，k分别代表地面坐标系的单位矢量。当单位时间Δt无限小时，飞机实际进行一个螺旋运动，此时，飞机的运动方向和机体方向的夹角固定，飞机运动速度大小固定为|V|，且飞机在单位时间绕机体坐标系x轴的旋转角度固定，即迎角和滚转角速度保持不变，飞机侧滑角则固定为0。由于飞机运动速度大小保持不变，速度方向在机体坐标系下固定，迎角、侧滑角和滚转角速度均保持不变，因此在机体坐标系下，这个过程的流动是稳态的，流场状态不随时间发生变化。该螺旋运动过程中，飞机整体的前进速度为速度平行于机体坐标系x轴方向的分量，滚转角速度矢量为ω，绕轴线速度为|V|sinα，计算可得半径为

因此该过程可用基于旋转坐标系的定常方法计算，来流速度为|V|cosα，方向与旋转轴同向，旋转半径为，旋转中心点为表示力矩中心点。此时可通过准定常计算方法计算非零迎角下的滚转运动气动力。计算两个不同滚转角速度的气动力，通过式（2）即可得到非零迎角下的滚转动导数。

1.2 任意方向阻尼动导数计算方法

对于任意迎角、侧滑角和任意俯仰角速度、偏航角速度和滚转角速度及其线性组合，也可采取类似方法计算动导数。首先建立一个坐标系，x轴为机体旋转轴，按右手螺旋定则与飞机旋转方向重合，在该坐标系下将自由来流方向矢量V分解为平行于该坐标系x轴Vx和垂直于该坐标系x轴Vn两个分量，计算旋转半径为，其中ω为俯仰角速度、偏航角速度和滚转角速度的线性组合，旋转中心点P=其中PM为力矩中心点，即可计算任意旋转轴和来流方向下的气动力。通过计算两个不同角速度下的气动力和式（2）求出动导数。

2 欧洲动导数标模（DLR-F12）动导数计算

2.1 计算模型

欧洲动导数标模（DLR-F12）是由德国航空航天中心（DLR）研制的标准空气动力学模型，机翼参考面积S=0.4441m2，平均气动弦长c=0.252625m，展长b=2.03852m，力矩参考点x坐标xM=1.04882m，z坐标zM=-0.03029m。该模型在德国-荷兰风洞（DNW）进行了一系列风洞试验[22]，模拟风洞试验来流速度V∞=70m/s，雷诺数Re=1.2×106情形。对DLR-F12 标准模型进行非结构网格的划分，其中Euler方程计算网格机身和机翼表面共416598个三角形，计算域共5871138个四面体，RANS方程计算网格机身和机翼表面共232108个三角形，计算域共7263616个三棱柱和2746623个四面体。计算条件与试验条件相同，即马赫数Ma=0.20597，雷诺数Re=1.2×106。采用Euler方程和RANS方程进行气动力和滚转、俯仰和偏航阻尼动导数CFD 计算，其中RANS 方程采用剪切应力输运（SST）湍流模型。DLRF12标准模型的Euler表面网格划分如图6所示。

图6 DLR-F12模型Euler表面网格划分及其局部放大示意图Fig.6 Euler surface mesh division and local zoom-in of DLR-F12 model

本文分别对改进方法和参考文献[10]的方法进行CFD求解，获得定常气动力以及滚转、俯仰和偏航阻尼动导数。

2.2 定常气动力计算结果

采用以上模型进行Euler 方程和RANS 方程的定常气动力计算，并与风洞试验数据及其他CFD计算结果进行对比。计算迎角为-5°～8°（间隔为1°）。计算结果及其与风洞试验和其他CFD 计算结果的升力系数（CL）和俯仰力矩系数（Cm）对比如图7所示。图中风洞试验数据和其他CFD计算结果由参考文献[22]提供。

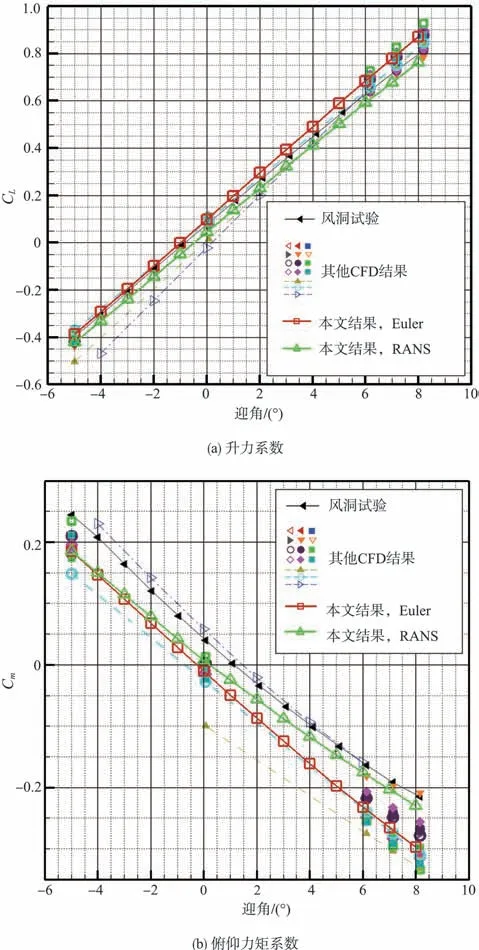
图7 定常气动力计算结果及其与风洞试验和其他CFD计算结果对比Fig.7 Steady aerodynamic coefficient computation vs wind tunnel test vs other CFD results

从计算结果可以看出，升力系数与风洞试验和其他CFD计算结果基本吻合，Euler方程俯仰力矩系数与风洞试验结果存在一个截距的差异，RANS 方程俯仰力矩系数在迎角较小时与风洞试验结果存在一定差异，在迎角较大时与风洞试验结果较为接近，与其他CFD 计算结果基本吻合。定常气动力计算结果验证了本文使用的CFD 计算程序的有效性。

2.3 动导数计算结果

2.3.1 不同旋转角速度的动导数计算结果

以滚转和偏航阻尼动导数为例，采用不同的迎角和不同的旋转角速度计算滚转阻尼动导数和偏航阻尼动导数，最大旋转角速度选用风洞试验时出现的最大旋转角速度。以Euler 方程为例，不同滚转角速度（p）下滚转阻尼动导数（Clp）的计算结果以及不同偏航角速度（r）下偏航阻尼动导数（Cnr）的计算结果如图8所示。

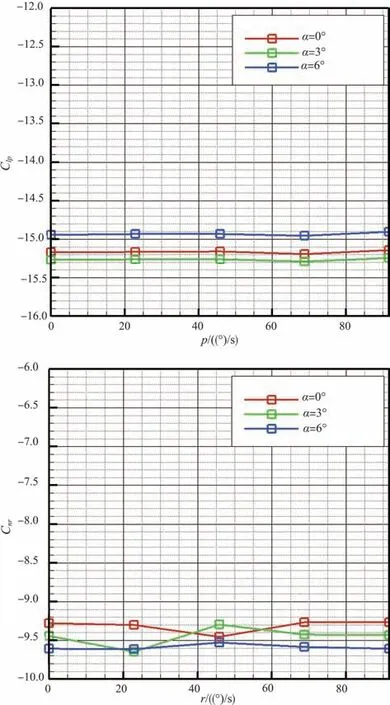
图8 不同角速度下滚转阻尼和偏航阻尼动导数结果Fig.8 Roll damping derivatives and yaw damping derivatives with different angular velocity

可以看出，在旋转角速度不大于风洞试验时出现最大旋转角速度时，滚转阻尼动导数和偏航阻尼动导数随旋转角速度变化较小，且不存在明显的增减趋势，因此，可采用多个不同角速度的阻尼动导数计算结果取平均值得到最终的阻尼动导数。后续阻尼动导数的计算均采用不同旋转角速度的阻尼动导数取平均值获得。

2.3.2 参考文献[10]计算方法的结果及其处理

为验证本文提出的方法的正确性，对参考文献[10]提出的方法进行CFD计算，将计算结果进行处理并和改进方法对比。以滚转阻尼动导数为例，对于非零迎角下的滚转阻尼动导数的计算，参考文献[10]采用的方法是计算绕风轴系x轴滚转的滚转阻尼动导数及交叉动导数，同时计算绕风轴系z轴偏航的偏航阻尼动导数及交叉动导数，使用式（3）进行计算结果的处理，求得体轴系下的滚转阻尼动导数。以滚转角速度p=91.61(°)/s 为例，参考文献[10]计算方法的绕风轴滚转力矩系数（Cl）和偏航力矩系数（Cn）计算结果及其绕体轴动导数处理结果分别见表1和表2。

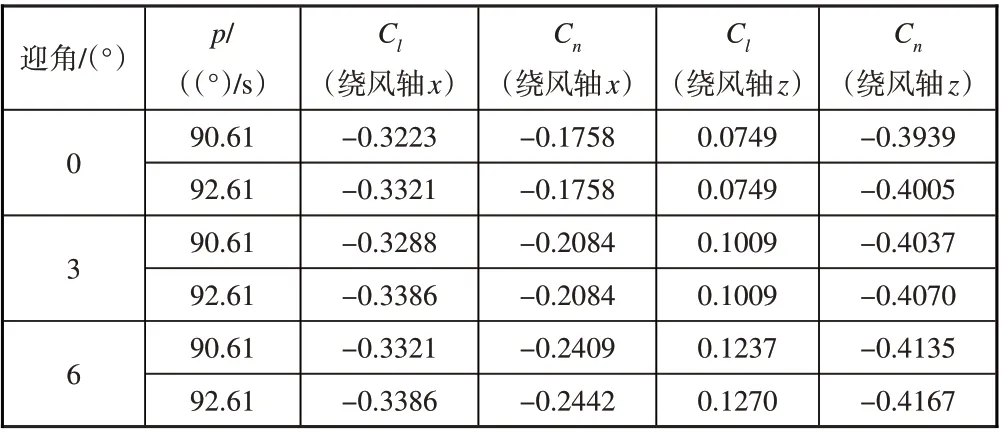
表1 参考文献［10］方法动导数计算结果Table 1 Dynamic derivatives computation results using ref.［10］method

表2 参考文献［10］方法动导数处理结果Table 2 Dynamic derivatives process results using ref.［10］method

类似地，其他状态下的阻尼动导数也可使用以上方法处理得到。

2.3.3 计算结果对比

将本文计算方法的计算结果、风洞试验结果、参考文献[10]方法的计算结果和其他CFD计算结果进行对比。滚转阻尼动导数、升力系数对俯仰角速度q动导数CLq、俯仰阻尼动导数Cmq和偏航阻尼动导数对比结果分别如图9～图12所示，图中风洞试验数据和其他CFD 计算结果由参考文献[22]提供，其中风洞试验数据为组合动导数。参考文献[22]中未提供改变侧滑角的CLq和Cmq的风洞试验数据和其他CFD计算结果。由于改变迎角的俯仰阻尼动导数计算使用参考文献[10]的方法也可通过两次计算得到一个状态的动导数，本文并未进行改进，因此这一情况只将改进方法与风洞试验数据和其他CFD计算结果进行对比。

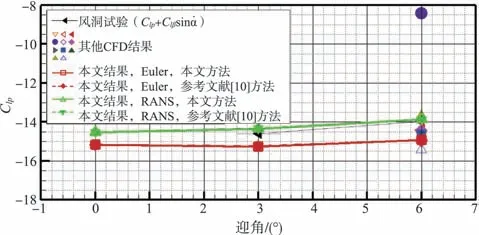
图9 改进方法、参考文献[10]方法、风洞试验和其他CFD计算的滚转阻尼动导数结果对比Fig.9 Roll damping derivatives result and comparison of our method,ref.[10]method,wind tunnel test and other CFD results

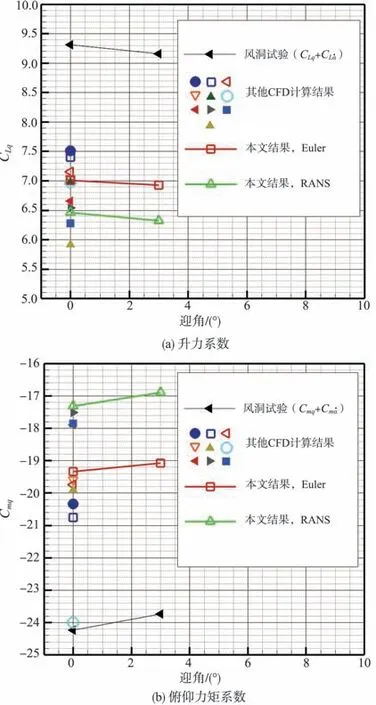
图10 不同迎角下改进方法、风洞试验和其他CFD计算的俯仰运动主要动导数结果对比Fig.10 Main pitch dynamic derivatives result and comparison between our method,wind tunnel test and other CFD results with different angle of attack

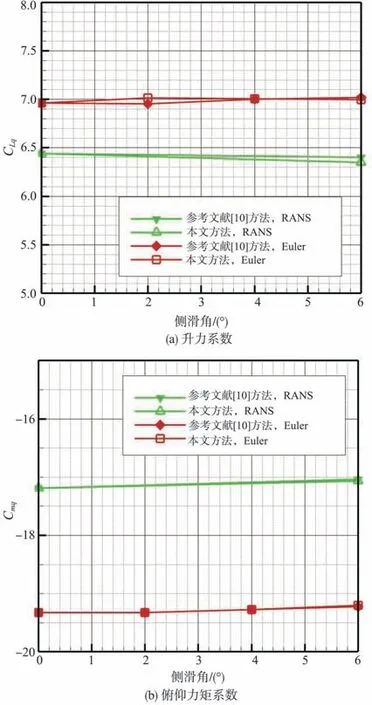
图11 不同侧滑角下改进方法和参考文献[10]方法计算的俯仰运动主要动导数结果对比Fig.11 Main pitch dynamic derivatives result comparison of our method and ref.[10]method with different angle of sideslip

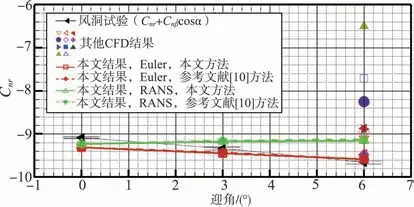
图12 改进方法、参考文献[10]方法、风洞试验和其他CFD计算的偏航阻尼动导数结果对比Fig.12 Yaw damping derivatives result and comparison of our method,ref.[10]method,wind tunnel test and other CFD results

可以看出，在滚转、俯仰、偏航三个方向上，无论是Euler方程还是RANS方程，改进方法的计算结果均与参考文献[10]方法的计算结果高度吻合。此外，改进方法计算结果均与其他CFD计算结果相差不大，滚转阻尼动导数和偏航阻尼动导数计算结果与试验数据基本吻合，但偏航阻尼动导数的RANS方程计算结果随迎角变化的趋势与风洞试验结果存在一定差异。俯仰运动的升力系数对俯仰角速度动导数和俯仰阻尼动导数计算结果与风洞试验数据存在系统性偏差，但计算结果随迎角的变化趋势与风洞试验相同。本文主要针对参考文献[10]的阻尼动导数计算方法进行改进，风洞试验和CFD的系统性偏差是一个专门的研究领域，不在本文研究范围内。

3 跨声速巡航标模（TCR）动导数计算

3.1 计算模型

跨声速巡航标模（TCR）是由瑞典萨伯（SAAB）公司研制的标准空气动力学模型，机翼参考面积S=0.3056m2，平均气动弦长c=0.2943m，展长b=1.1165m，力矩参考点x坐标xM=0.87475m。该模型在俄罗斯中央空气流体力学研究院（TsAGI）进行了一系列风洞试验[23]，风洞试验来流速度V∞=40m/s，雷诺数Re=7.9×105。对TCR标准模型进行非结构网格的划分，其中Euler方程定常计算网格机身和机翼表面共172550个三角形，计算域共2280959个四面体，动导数计算网格机身和机翼表面共159740 个三角形，计算域共2046552个四面体；RANS方程定常计算网格机身和机翼表面共172382 个三角形，计算域共5516224 个三棱柱和1979151 个四面体，动导数计算网格机身和机翼表面共138814个三角形，计算域共4442048个三棱柱和3074231个四面体。计算条件采用与试验条件相同的计算条件，即马赫数Ma=0.1179，雷诺数Re=7.9×105。采用Euler 方程和RANS 方程进行滚转阻尼动导数CFD 计算，其中RANS 方程采用SST湍流模型。TCR标准模型的表面网格划分及其局部放大如图13所示。

图13 TCR模型表面网格划分及其局部放大示意图Fig.13 Euler surface mesh division and local zoom-in of TCR model

参考文献[24]中已采用TCR 模型进行Euler 方程和RANS方程的定常气动力计算，本文采用与参考文献[24]相同的计算软件和计算网格，分别对改进方法和参考文献[10]的方法进行CFD 求解，获得滚转、俯仰和偏航阻尼动导数。

3.2 定常计算结果

参考文献[24]的定常计算结果及其与风洞试验的法向力系数（CN）和俯仰力矩系数对比如图14所示。

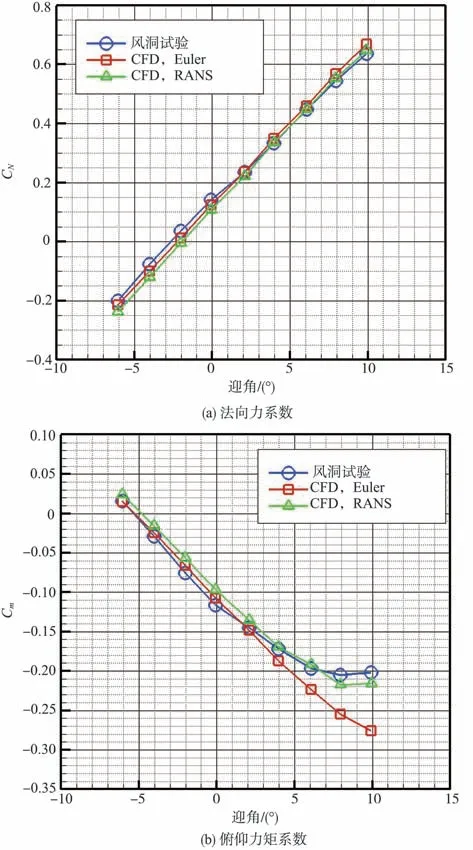
图14 气动力系数的定常计算结果及其与风洞试验对比Fig.14 Steady computation of aerodynamic coefficient and comparison with wind tunnel test

结果显示，法向力系数计算结果与风洞试验数据高度吻合，俯仰力矩系数计算结果在-6°～2°迎角工况下与风洞试验数据基本吻合，在迎角≥4°情况下存在系统性偏差。由于本文主要将改进的阻尼动导数计算方法和参考文献[10]的阻尼动导数计算方法进行对比，因此计算结果满足本文研究要求。

3.3 动导数计算结果

采用2.3.1和2.3.2节介绍的处理方法，对改进方法和参考文献[10]方法的计算数据进行处理。将改进方法的计算结果、参考文献[10]方法的计算结果及风洞试验结果进行对比。滚转阻尼动导数、法向力系数动导数CNq、俯仰阻尼动导数和偏航阻尼动导数对比结果分别如图15～图17 所示，其中滚转阻尼动导数、偏航阻尼动导数的风洞试验数据为组合动导数。

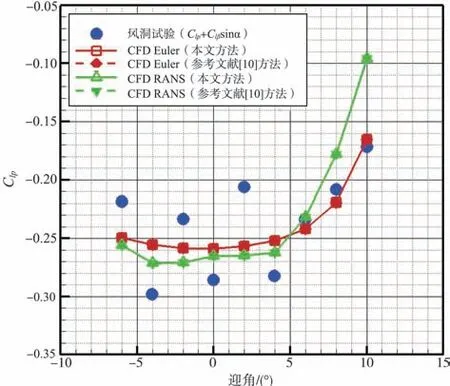
图15 改进方法、参考文献[10]方法滚转阻尼动导数结果和风洞试验结果对比Fig.15 Roll damping derivatives result comparison between our method,ref.[10]method and wind tunnel test

图16 改进方法和文献[10]方法法向力系数相对俯仰角速度动导数和俯仰阻尼动导数结果对比Fig.16 Pitch rate-normal force coefficient derivatives and pitch damping derivatives result comparison between our method and ref.[10]method

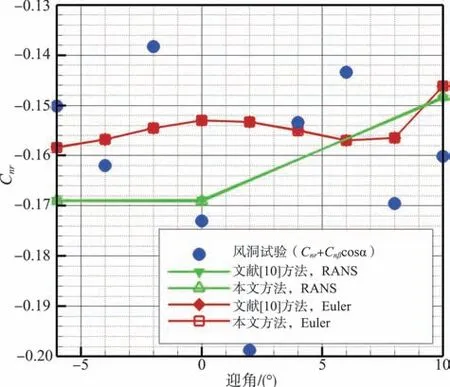
图17 改进方法、参考文献[10]方法偏航阻尼动导数结果和风洞试验结果对比Fig.17 Yaw damping derivatives result comparison between our method,ref.[10]method and wind tunnel test

可以看出，在计算TCR 标准模型时，改进方法的计算结果在滚转、俯仰、偏航三个方向上均与参考文献[10]方法高度吻合。本文的计算方法计算得到的动导数和风洞试验数据存在系统性偏差，现象为风洞试验数据值围绕计算结果跳跃。造成差异可能的原因有风洞试验结果包括了侧滑角变化率的影响，以及风洞试验和计算的精度原因。