矩形波导中模式分类的讨论
2022-07-30秦薇敏
王 楠 邓 鉴 秦薇敏 苏 涛
(西安电子科技大学 电子工程学院, 西安 710071)
矩形波导是导波系统中重要的传输线类型之一,在电磁场与微波课程教学中,它前承以电路为基础的传输线理论,后启微波工程中特有的微带等导波元件,是课程教学中的重要内容[1-2]。
在目前通用的课程教材中,对金属波导中的模式,根据电磁场的纵向分量(Ez,Hz)进行分类为:TE模式(Ez=0,Hz≠0)、TM模式(Ez≠0,Hz=0)、TEM模式(Ez=0,Hz=0),并且指出按纵向分量分类的三种波型是最实用的[3]。然而很明显的是,按照纵向分量的取值分类,还应该提及存在纵向电场和纵向磁场,也即Ez≠0,Hz≠0的混合模式,这也是课程学习者经常提出的问题之一。已经证明,在空心金属波导中不存在TEM模式[4],本文使用反证法,证明矩形波导中不存在Ez≠0,Hz≠0的混合模式。本文的推导可以为电磁场以及微波等相关课程教学给出有益的参考。
1 模式的推导

图1 待求解的矩形波导

(1)
纵向分量法分为两个部分的内容,第一步由麦克斯韦方程组推导出横向分量和纵向分量之间满足的相互关系,用矩阵方程表示[3-4]:
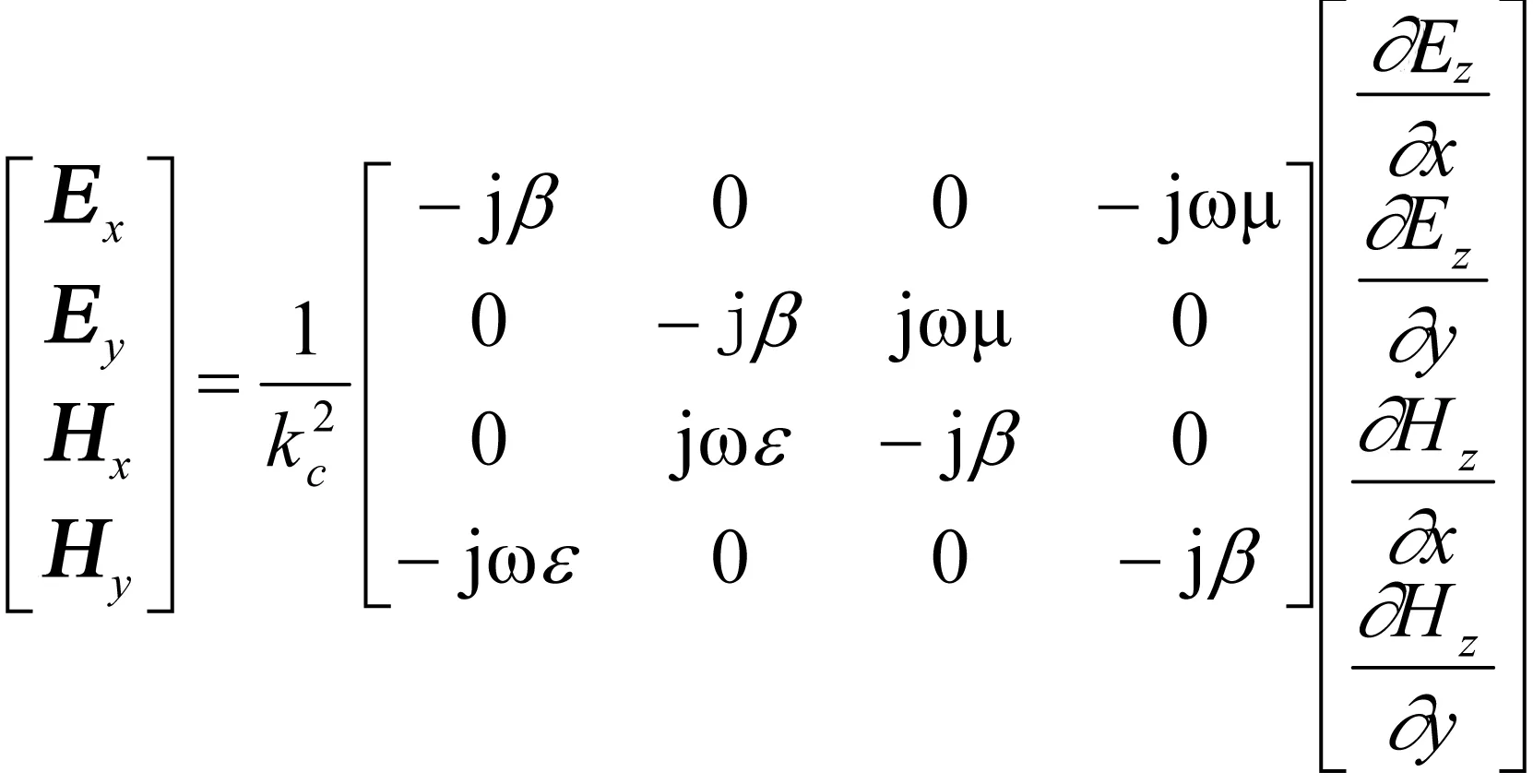
(2)
由式(2)可知,求解Ez,Hz即可得到所有电磁场分量,求解方法即是纵向分量法的第二步,分离变量法求解纵向分量。
在TE模式和TM模式之外,假设存在Ez≠0,Hz≠0的混合模式,接下来对混合模式的电磁场分量进行求解。
通过分离变量法[5]可以写出
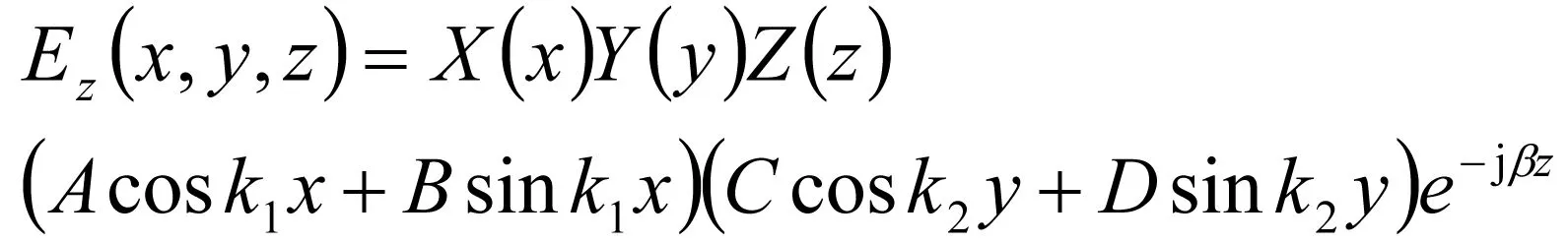
(3)
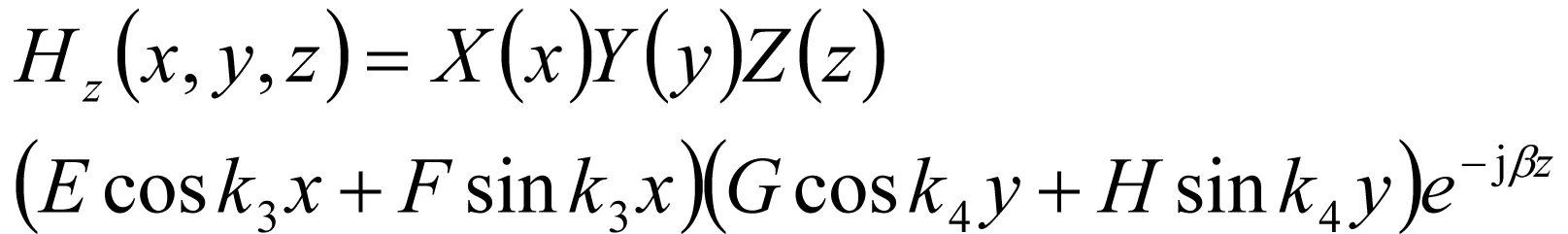
(4)
其中的A,B,C,D,E,F,G,H和k1,k2,k3,k4由具体边界条件解出。
根据理想导体边界条件可知,矩形波导边界条件为
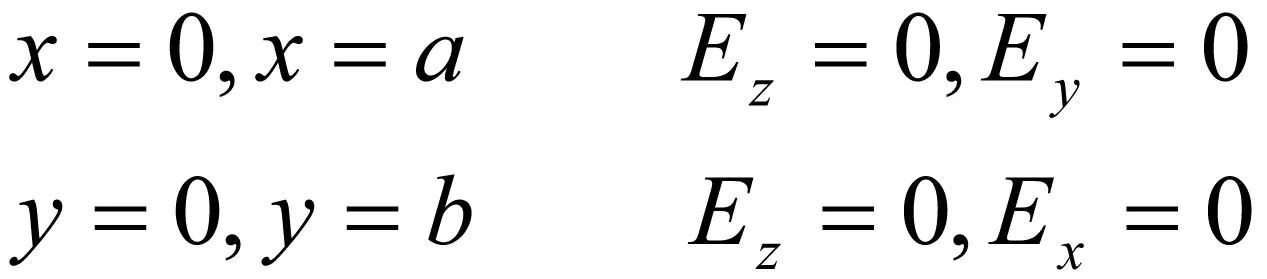
(5)
首先利用Ez的边界条件,也即
34例患者中有29例首次应用唑来膦酸后未再次使用,2例患者在预防性静脉输注地塞米松及泼尼松龙滴眼液后,再次使用唑来膦酸治疗未出现眼部不适[5]。1项回顾性临床调查[20]中,8例急性葡萄膜炎患者中有3例在发生唑来膦酸相关性急性葡萄膜炎18个月后,在未给予任何预处理的情况下再次应用唑来膦酸治疗,未再出现眼部症状及体征[22]。
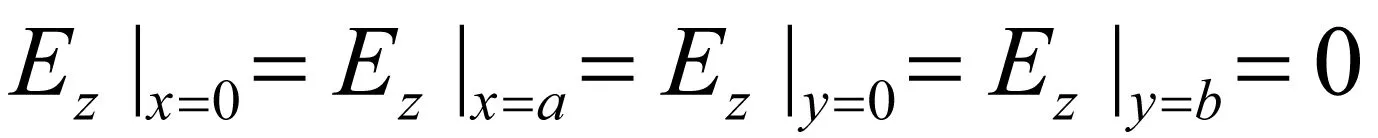
(6)
可以解出
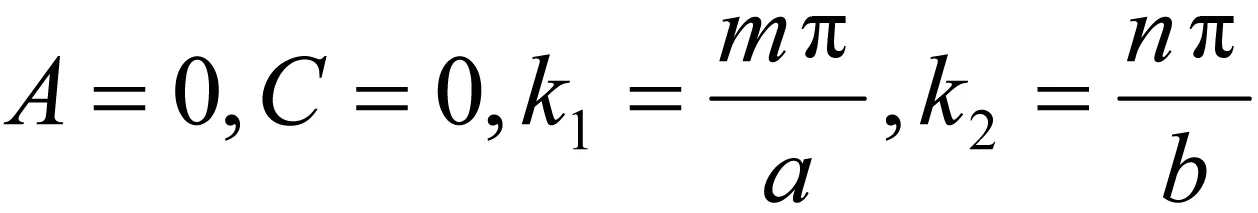
(7)
可得
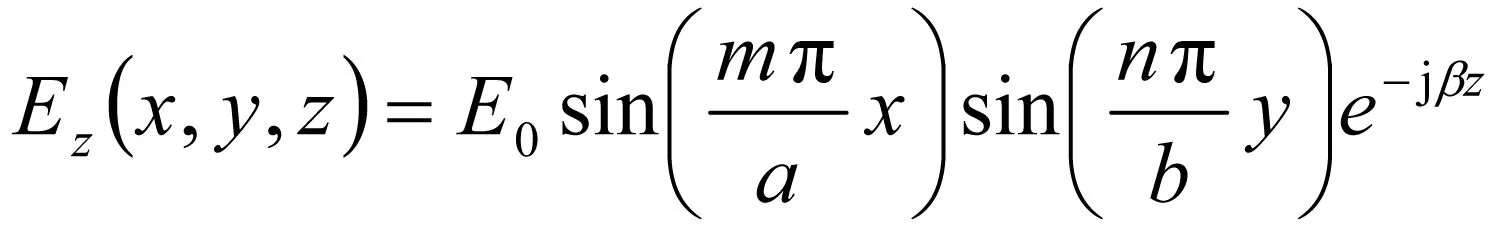
(8)
其中m=1,2,…,n=1,2,…为整数。
然后利用Ez和Ey的边界条件
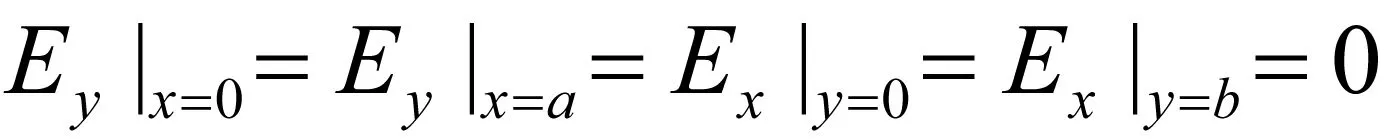
(9)
由式(2)可得
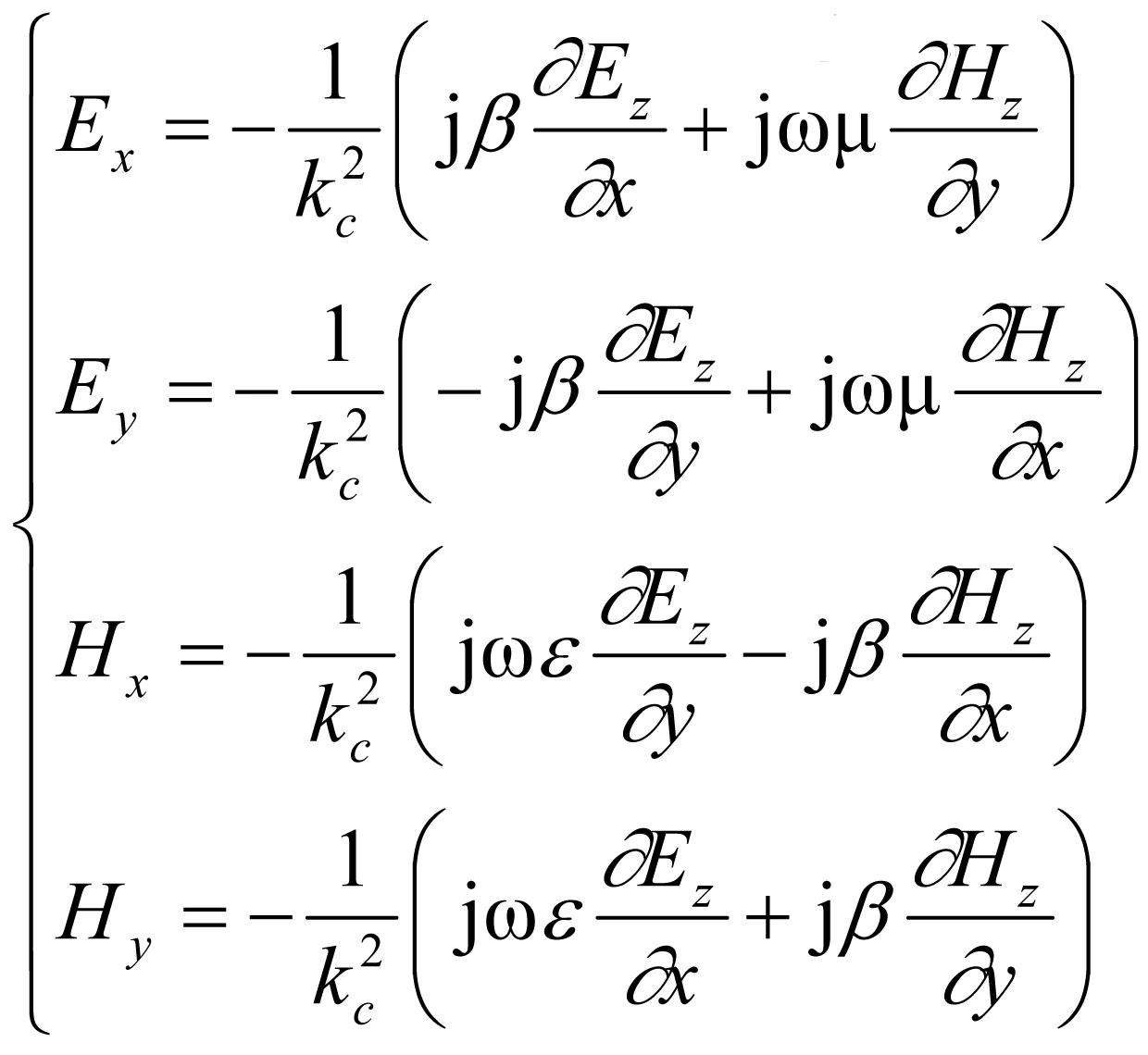
(10)
可以解出

(11)
可得

(12)
其中p=0,1,2,…,q=0,1,2…为整数。
最终可以得到混合mnpq模式的电磁场分量为
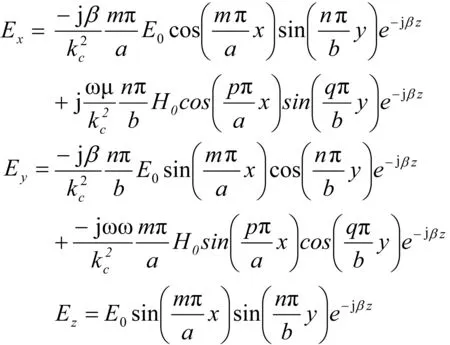
(13)
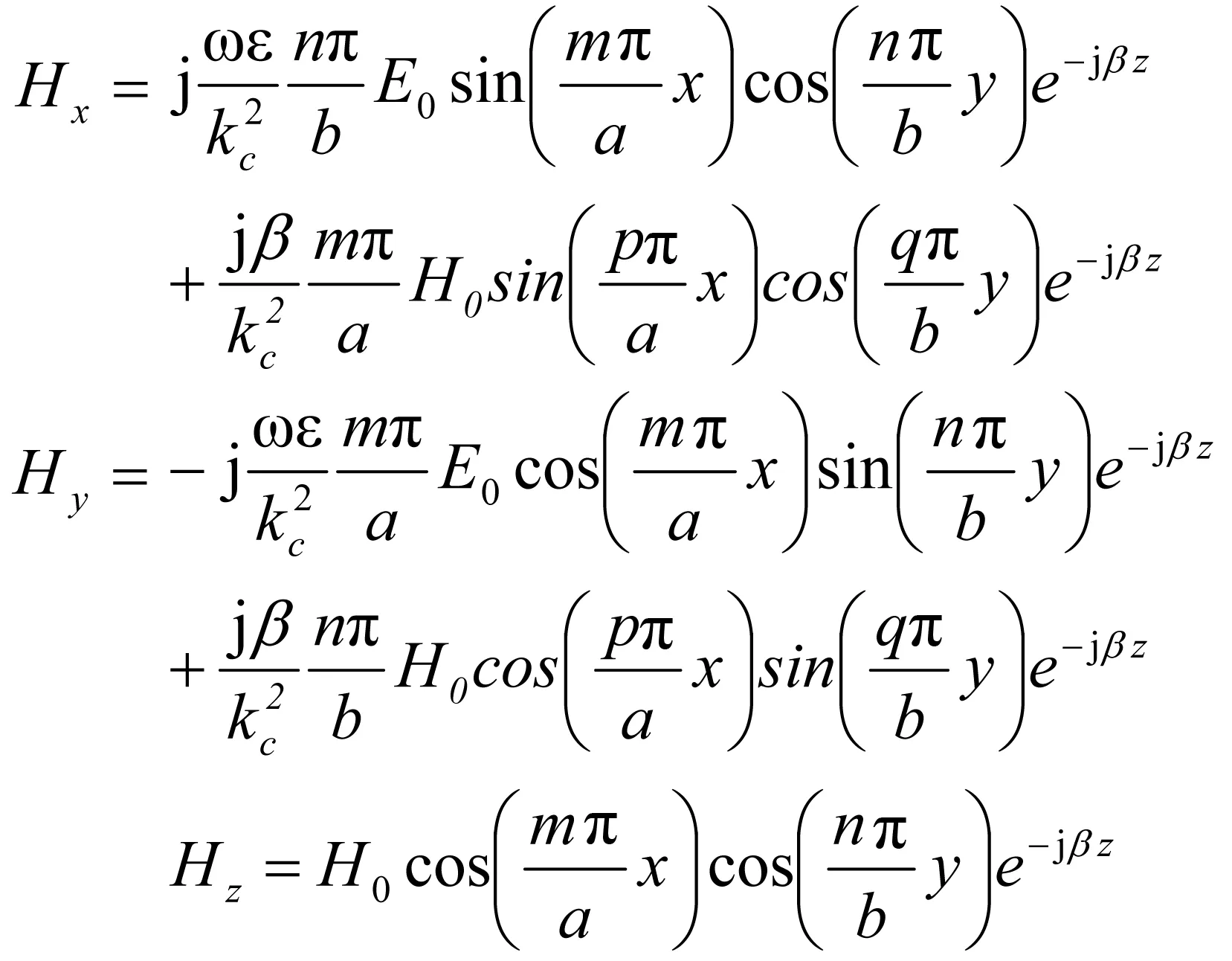
(14)
2 独立性的讨论
讨论传输功率

(15)
将式(13)和式(14)代入可得任意mnpq模式下的传输功率
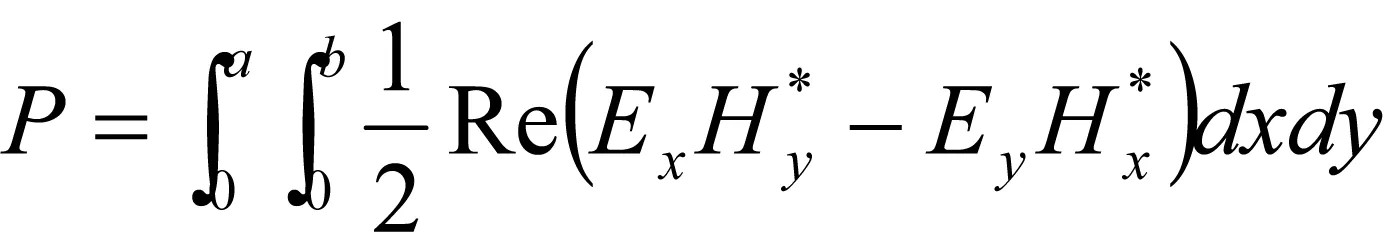
(16)
被积函数第一项:

(17)
被积函数第二项:

(18)
在傅立叶变换中可知

(19)
式(17)积分可以得到

(20)
式(18)积分可以得到
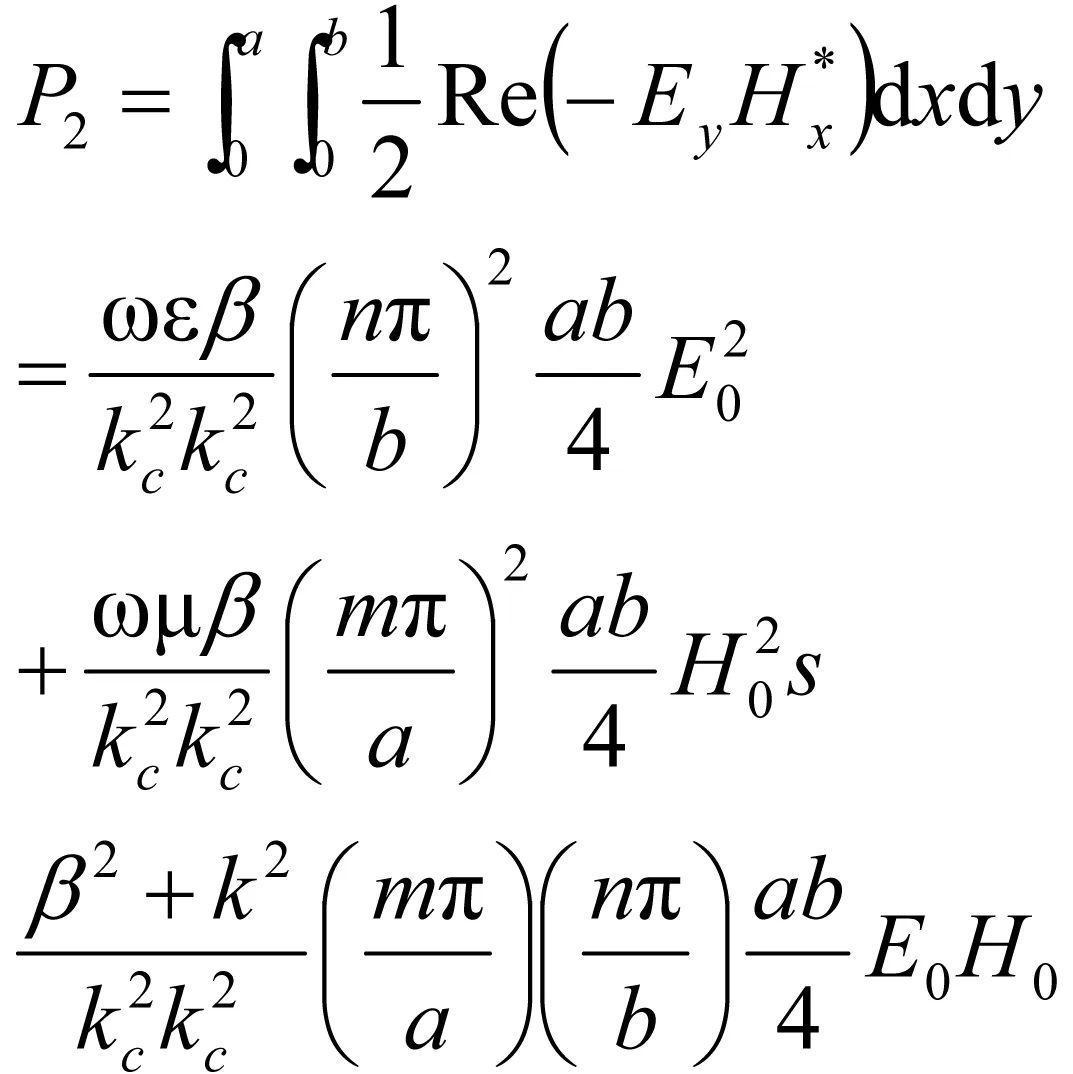
(21)
可得传输功率为

(22)
从式(22)中可以看出,首先,电领矢和磁领矢之间相互独立,其次,第一项是矩形波导中TMmn模式的传输功率,第二项是矩形波导中TEmn模式的传输功率[3-4]。可见纵向电场领矢的电磁场与纵向磁场领矢之间的电磁场之间并不存在能量的相互交换,总的传输能量是TMmn和TEmn传输能量之和,因此矩形金属波导中不存在纵向电场和纵向磁场都存在的混合模式。
3 结语
从“电磁场与微波”课程教学实际出发,对经典的导波传输线矩形波导中的模式分类进行讨论。使用纵向分量法求解电磁场的分量,利用反证法证明了在矩形金属波导中不存在纵向电场和纵向磁场都存在的混合模式。本文给出的推导证明有利于在教学中辅助学习者对矩形波导和导波系统的理解,也可以作为课程教学的有益参考。
