几何视角下的“数字信号处理”课程

余 磊 张海剑 夏桂松

(武汉大学 电子信息学院， 武汉 430072)

“数字信号处理”课程作为电子电工类专业信号处理方向的基础课，要求学生深入理解基本概念，扎实掌握应用方法。该课程是一门理论性很强的基础专业课程，概念抽象、公式繁多、内容和知识体系繁杂[1-4]。因此，有必要对“数字信号处理”课程进行体系框架的梳理和更新。在理论课程体系方面，金伟等人针对数字信号处理理论性强、公式繁杂以及用专业例证解释存在学习时间差等问题，给出了卷积物理本质的解释，加深了学生对卷积概念的理解[5]。刘大年等人依据“数字信号处理”课程的特点和学生的心理规律，阐明了形象化教学的必要性，提出了形象化教学的原则,这些工作对培养学生的直觉思维具有积极作用[6]。王秋生等人针对“数字信号处理”课程建设存在的实际问题，从授课内容、课程实验、课后作业、考核方法、教学团队等多方面，系统地阐述了面向工程实践理念的“数字信号处理”课程建设原则、建设方法、建设成果以及对培养学生能力的促进作用[7]。在实践课程体系方面，杨长生等人借鉴欧美等国家的高阶思维内涵，分析了“数字信号处理”课程的教学现状，结合国内高校的教育环境进行针对性的课程设计[8]。孙锐等人阐述了教学过程中的一些典型案例，通过面向实际问题和学科前沿的研究案例,增强了学生对知识的应用能力,而了解更多的学术前沿研究成果,有助于启发学生创新性思维[9]。王艳芬等人则指出了课程改革的总体目标及具体思路，重点介绍了运用Matlab进行课程教学的教学改革步骤与实施过程，实践证明，该改革具有自己的特色，取得了显著成效[10]。针对应用型人才培养过程中存在的学生知识体系不完整，工程实践能力弱等问题，丑永新等人基于企业用人需求及实际工程案例对信号类课程进行改革[11]。

教学实践结果表明，所提出的信号类课程教学改革有效地提升了学生的科技创新及工程实践能力。

然而，目前的课程内容大多从经典视角出发，具有如下特征：

课程中心“系统”化：在经典课程体系下，“数字信号处理”以“系统”为中心，围绕系统的输入、输出和性质分析，从时域和频域开展讨论，包括时域和频域变换、采样重建和滤波器设计。这种面向系统的课程体系在数字信号处理发展的初期(20世纪60年代至90年代末)是合理且可行的[4,12]。原因在于，如何利用数字方法替代模拟方法是当时数字信号处理面临的问题，解决该问题可以提升系统的鲁棒性和可移植性。随着信息化和人工智能时代的到来，目前该领域所面临的主要问题已经从“如何替代模拟方法”转化为“如何从数字信号(数据)本身提取有用信息”，例如多源、高维、异构数据所带来的复杂特征提取和语义信息检索等问题[13]。

课程方法“代数”化：作为“数字信号处理”课程的承接课程，“数字图像处理”“语音信号处理”“信号检测与估计”，以及研究生阶段的“现代信号处理”等课程中，空间、正交、完备等几何概念逐渐成为信号处理理论前沿研究的基础，例如主成分分析、稀疏表示、低秩矩阵分析等[14]。现有经典课程体系仅介绍信号和系统的代数定义，缺乏对这些代数定义的几何解释。虽然本科阶段的“数字信号处理”课程没有涉及这些复杂的信号处理方法，但建立几何视角下的“数字信号处理”理论体系，能帮助学生更直观地理解代数理论下的几何本质，为进一步学习更复杂的信号处理理论奠定基础。

“系统”化和“代数”化的课程体系强调：课程内容以系统为研究中心，以离散信号傅立叶变换、z变换和离散傅立叶变换为分析工具，以滤波器设计为主要目的，课程讲解注重定理和公式推导及其性质分析。由于概念繁杂，这种经典视角下的课程内容安排难以给学生建立一个宏观的整体概念，导致知识体系碎片化的问题。同时，相对枯燥的代数推导过程，也极大地降低了学生的学习兴趣。

针对以上问题，笔者从几何视角引入对经典数字信号处理基本概念的重定义，建立“数字信号处理”课程体系，提高学生的学习兴趣，加深其对基本概念的理解。英国数学家Michael Atiyah在《二十世纪的数学》中将代数与几何比喻成耳朵和眼睛，代数的目标往往集中于建立一个公式，而丢掉了洞察力[15]。然而，绝不能放弃这些洞察力！传统的教学方法注重代数推导，却忽略了几何描述，即如同我们失去了双眼。而分析认为，人们通过视觉的接受和理解能力远远超过了听觉。因此，从几何视角重构的新课程体系，能够有效去除经典课程体系中“系统”化和“代数”化的壁垒，建立更为简洁的面向“信号”的“几何”知识体系，并在教学过程中提升学生对本质问题的“洞察力”。

基于多年的科研基础和教学经验，笔者从课程特点和发展趋势出发，在现有课程体系框架中，引入对课程核心内容(信号时域/频域表示、采样定理和线性时不变系统)的几何描述，让学生洞察到隐藏在这些理论和概念背后的几何原理[14-17]。

1 几何基础

长度为N的有限长离散时间信号x[n]表示时刻为n时的样本。我们也可以将这N点样本表示成 维复空间中的向量

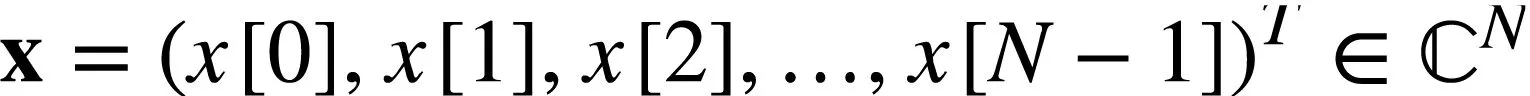
(1)

(2)

公式(1)可以理解为信号的分解过程，公式(2)可以理解为信号的合成过程。信号的分解过程通过计算信号在基向量上的分量来分析信号的性质；信号的合成过程利用基向量线性组合来表示信号向量。基于上面的信号分解和合成，我们可以从几何视角对“数字信号处理”课程中的几个重要概念进行重构。

2 几何视角下的“数字信号处理”课程

2.1 信号时域表示

时域离散信号可以表示为单位脉冲序列的延迟加权叠加

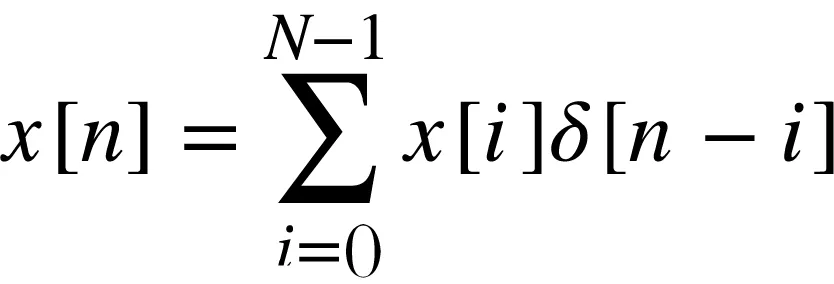
(3)

写成向量的形式为

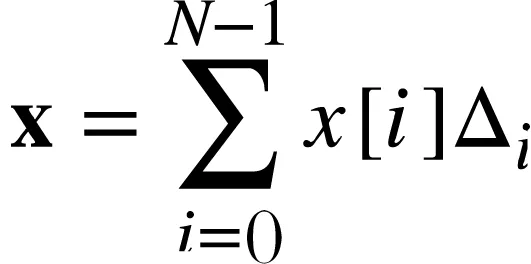
(4)

(5)

2.2 信号频域表示

对离散时间信号进行离散时间傅立叶变换(DTFT)可以得到信号的频域表示

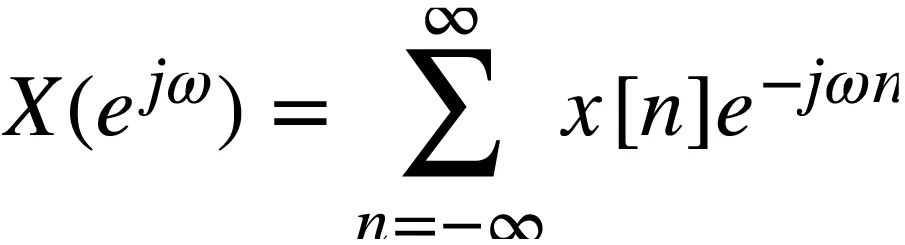
定义bω[n]ejωn，那么DTFT变换可以表示为如下内积形式

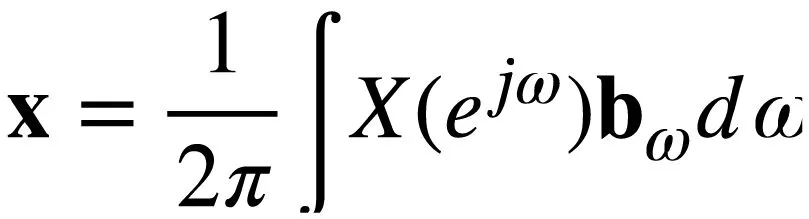
信号的时/频域表示是信号处理的基础，我们将这一问题的经典描述和几何描述分别列在表1中作为对比。

表1 信号的时/频域表示

2.3 连续时间信号的采样

连续时间信号x(t)的采样过程一般包括：抗混叠滤波、采样保持、AD转换。重建过程一般包括：DA转换和低通滤波重建。假设抗混叠滤波器的冲激响应为h(t)，滤波输出为

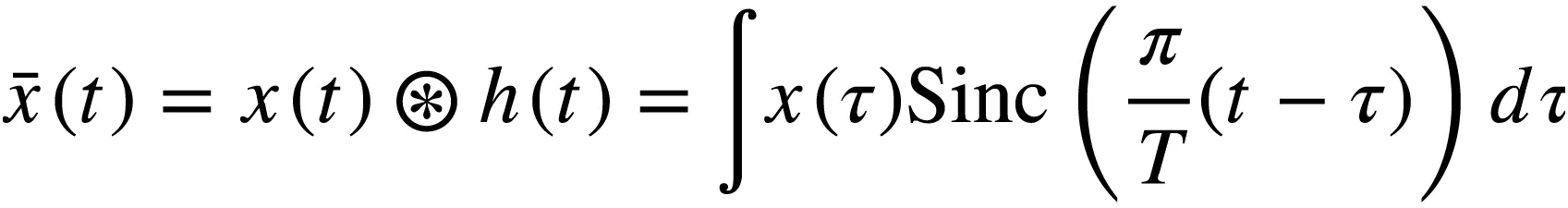
以周期T采样后得到离散时间信号x[n]为

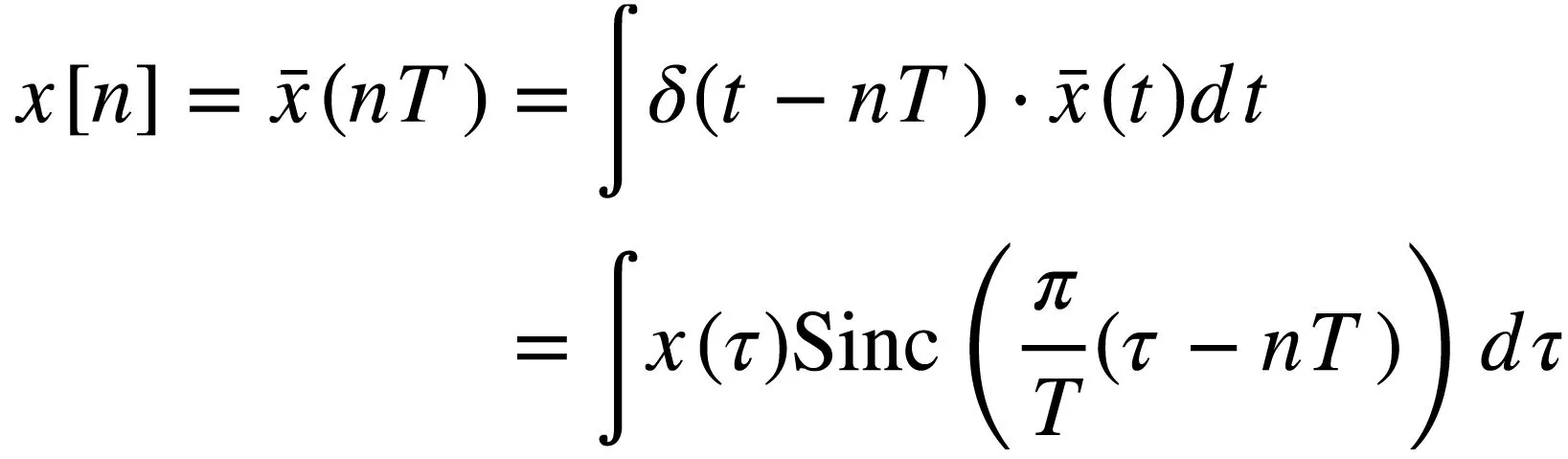
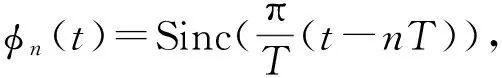
(6)

其中函数{φn(t)}n∈构成一组由Sinc函数组成的正交基向量，且φn(t)∈L2。定义基向量{φn(t)}n∈展成的空间为span{φn(t)}n∈∈L2，那么采样过程(6)可以看作是将连续时间信号 投影到基向量φn(t)的过程，对应的第n个投影坐标就是第n个样本值x[n]。

根据奈奎斯特采样定理，在时域中由离散样本重建连续时间信号的表达式为

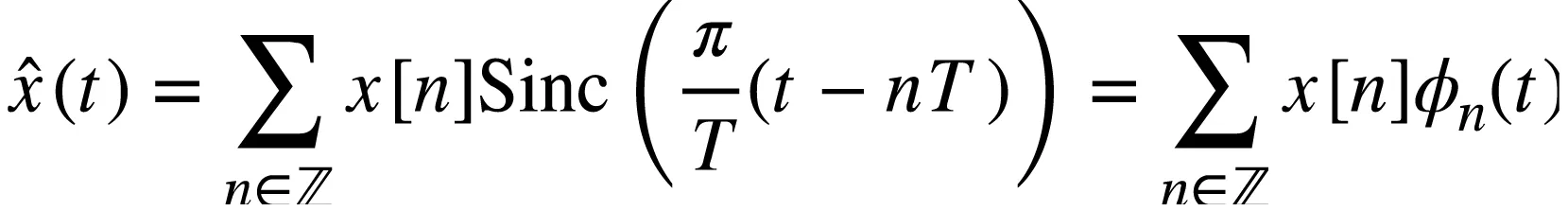
(7)

表2 采样定理的经典描述和几何描述对比

2.4 线性时不变系统

线性时不变系统的输出序列y[n]为输入序列x[n]和冲激响应序列h[n]的卷积

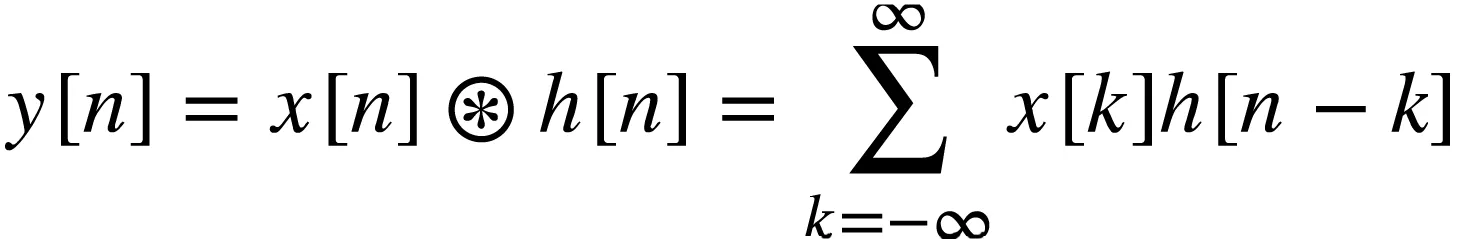
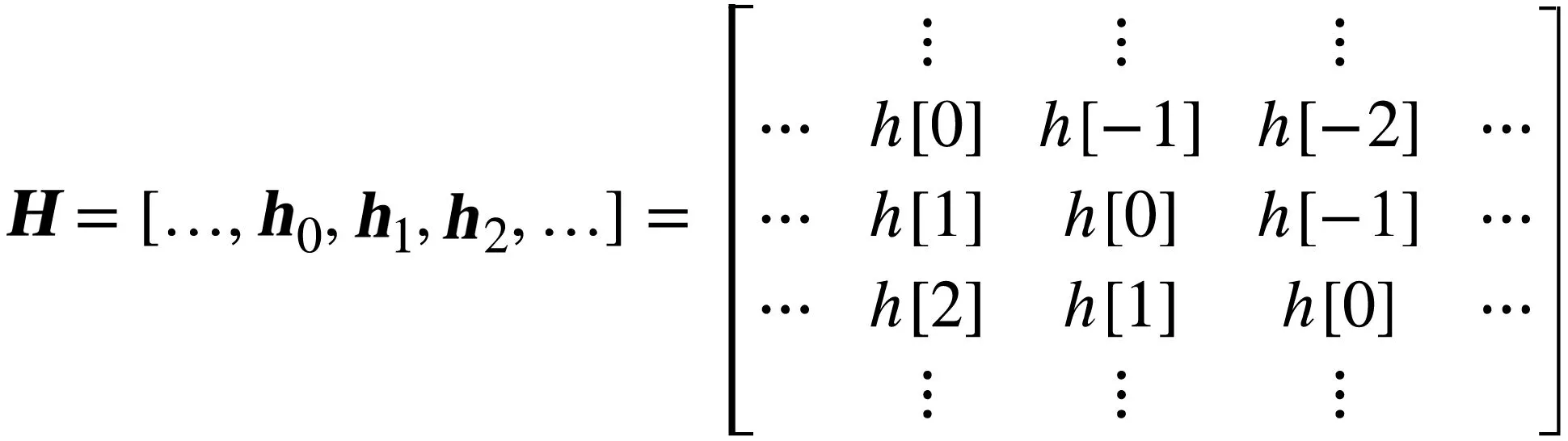
系统输入输出关系的向量形式为

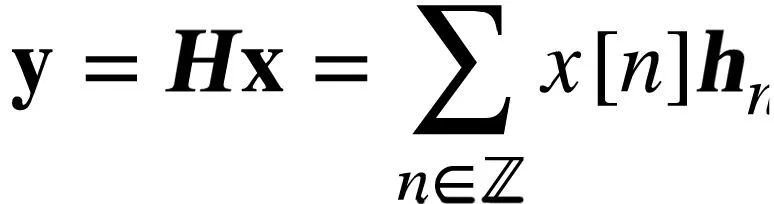
(8)

(9)

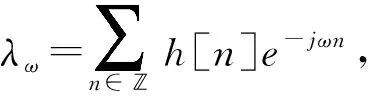
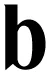
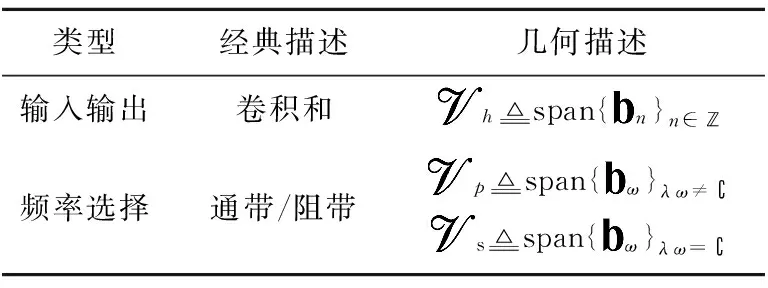
表3 线性时不变系统的经典描述和几何描述对比

3 基于几何视角课程体系的前沿拓展

基于表1-3中这些课程核心概念的几何解释，我们可以很容易的将现有学术前沿问题引入到课程教学中来，例如：

(2)采样过程的经典描述虽然能得到频谱周期延拓的结论，但是推导过程复杂，很容易让学生忽视了Nyquist定理的充分非必要性。另一方面，采样过程的本质内容是如何对连续信号进行离散表示，但学生学完采样定理后仅了解了Nyquist频率。从几何的角度可以很容易地分析出来；无失真重建和有失真(混叠)重建的本质内容是连续信号是否在采样所使用的基向量展成的空间中，如表2所示。同时，基于几何描述，是否存在其他的采样方式，其基向量与Sinc函数不同？从而引导学生去关注采样定理提出后的60余年间该领域的新发展，例如压缩感知理论[21]。

(3)在经典描述中，线性时不变系统的输出为输入和系统冲激响应的卷积和。由于卷积的交换律，学生在系统和信号之间很容易混淆，二者具有一定的不可分问题。在几何描述下可以发现，系统决定了输出信号所在的空间，而输入信号决定了输出信号在该空间中的位置。基于这一概念，可以引导学生进一步研究基于大量输出信号的盲系统辨识问题。

4 结语

针对经典体系中课程中心“系统”化和课程方法“代数”化所带来的碎片化问题，我们重新构建了以“信号”为中心的“几何”知识体系。通过引入几何视角下对信号和系统的描述，将经典课程体系中的概念和方法用几何框架中空间、正交、投影、合成等概念来重新定义。可以发现，几何视角的课程体系更系统、更本质地诠释了数字信号处理课程中的概念和方法。