电磁学的可视化仿真教学
2022-07-30王丹萍彭进业任宇辉
贺 晨 王丹萍 冯 筠 彭进业 任宇辉
(西北大学 信息科学与技术学院, 西安 710127)
电磁学研究的是电场、磁场各自的性质以及它们之间的相互作用,是物理学中的一个重要分支[1]。近年来,电磁学得到了高速发展,人们的研究方向也发生了质的改变,从电磁宏观转向了电磁微观[2]。因此在电磁理论与实验中,存在很多理论性强且抽象的概念以及难以构想的电场图和磁场图,这就不仅需要具有强大的数学知识储备来支持,还需要严谨的逻辑思维能力、空间构想能力等。比如在电磁学中,电场和磁场都是抽象的概念,学生没有办法用肉眼看到,这就给学生的理解造成了困难[3]。
目前,传统的“电磁学”课程的教学方式主要集中于理论与概念的讲授。但是在很多情况下,教师无法向学生展示抽象的电磁学物理模型。这就导致学生对基本概念的理解仍然存在一定的偏差,只注重数学层面的计算而忽视了物理实质[4]。目前以计算机为基础的可视化仿真技术在电磁学理论领域中已经得到了普遍的应用,这种技术使用特定的仿真软件将电磁学的物理概念建模为数学模型进行科学计算,计算机再将数据转换成静态或动态的图形显示出来,从而实现电磁学理论问题的可视化[5]。由此可见,电磁学可视化的理念除了可以进行复杂度很高的计算以外,还具备将抽象概念具体化的能力,将我们肉眼无法看到的抽象事物转变为精确度很高的仿真模型[6]。这一理念的出现给教师和学生都带来了巨大的便利,对于电磁学中无法观察的物理过程,通过建模仿真转化为图像呈现在学生面前,这样就可以直接观察到形象准确的模型,以便更深刻地理解其物理实质[7]。因此,电磁学可视化的出现对于教学的意义是不言而喻的。
为了使学生在学习过程中,既能掌握“电磁学”课程中的理论,又能利用计算机代码实现电磁学可视化仿真教学,结合人工分析计算和可视化仿真两种方法对“电磁学”课程实验中遇到的各类问题进行了建模计算和仿真。一方面希望在理解相关知识点的过程中,培养学生的数学思维和动手计算的能力;另一方面也希望利用易于理解的仿真实验方法,深入对电磁学知识的理解,让学生能够具有分析和解决电磁学问题的基本能力[8]。
1 电磁学的静态可视化
在分析电磁学问题时,我们需要具备一定的抽象思维。随时间变化的电场能够激发磁场,随时间变化的磁场也能激发电场,但是这种变化以及其中涉及到的概念都是抽象的,它们都是看不见也摸不到的,没有一定的形态、质量等,因此很难直接被我们理解[9]。接下来我们通过分别绘制电磁学中的电场、磁场来说明如何利用建模仿真实现图像的静态可视化[10]。
1.1 等势线和电场线的可视化仿真
问题描述:考虑如图1所示的导体结构和相应电势,试推导导体内部的点(x,y)处的电势表达式,并编写一个程序绘制等势线和电场线。

图1 导体结构及相应电势
首先通过分析计算,我们可以得到该导体电压的拉普拉斯方程为

(1)
接下来需要根据该方程进行建模和仿真。绘制等势线和电场线的伪代码如算法1所示。

仿真结果如图2和图3所示。
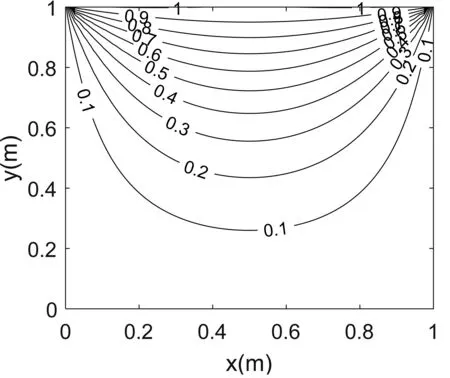
图2 在0 图3 在0 问题描述:如图4所示,以z轴为中心的环形线圈带有8.0 A的电流,匝数为200。内径为1.0 cm,外径为3.0 cm。编写程序计算并绘制在x-y平面上有界区域(-5.0 cm≤x≤5.0 cm和-5.0 cm≤y≤5.0 cm)的磁场大小。 图4 带有8.0 A电流的环形线圈 环形线圈的横截面如图5所示,这个问题要求我们在x-y平面上画出磁场,也就是说需要计算x-y平面上每个点的磁场(实际上不是每个点,而是尽可能多的点),并将这些值存储到一个二维矩阵中。我们可以给线圈上的每个点都指定一个特殊的角度值。例如,如果一个点(在圆柱坐标参数)的角度φ为π/3,那么在计算第三匝角度时,给这个点指定的角度值是在一般情况下,φ′=φ+2(k-1)π。其中k∈Z,1≤k≤匝数且0≤φ≤π。已知φ′的大小,可以求出第k匝上点的直角坐标: 图5 环形线圈的截面视图 (2) (3) (4) (5) 现在沿着电流I的方向将线圈分成许多段,以便可以编写程序计算磁场。假设要把这个线圈划分成n段,那么需要在线圈上选取n+1个点。对于第i点,可以求出该点的角度,再利用坐标公式计算该点处的磁场。 这一部分算法的伪代码如下: 为了验证仿真代码的准确性,以Matlab仿真软件为例,运行结果如图6所示,图像展示了由以z轴为中心的螺线管产生的磁场线,可以看出通过引入Matlab强大的绘图仿真功能,将大量的数据以仿真图形的形式展现出来,更加直观、清晰,容易接受,也进一步加深了学生对电磁场相关知识的理解。 图6 环形线圈在x-y平面上产生的磁场线 在“电磁学”课程的教学中,有很多物理概念仅靠静态的图像仍无法展示出其实质,很多学生对这类问题还是无法深入理解。比如在电磁波的教学中,电磁波是由于电场与磁场在空间中以波的形式移动而产生的,因此它的传输状态会随着空间和时间的变化而改变。为了更好地理解电磁波的这种波动性,我们需要利用图像的动态可视化来分析问题。 除此之外,在电磁波的教学中还存在一个重要的物理概念——极化。极化根据电场强度等物理量的不同可以分为很多种。这一部分知识由于内容理论性强且较为抽象,常被视为教学上的重、难点。学生在学习该部分知识时,仅靠理论概念和静态图形仍然难以想象出极化波具体的传导过程。利用常见的仿真软件可以实现动态图像的演示,不仅激发学生的学习兴趣,而且加强学生对电磁波和极化等概念的熟悉和理解。下面的例子说明了如何通过建模、计算演示电磁波及其极化[10]。 问题描述:某种无损材料μr=9且εr=16,一个10 MHz的均匀平面波以速度Ex0=323 V/m沿ay方向传播,t=60 ns时在点P(0.6,0.6,0.6)处有Ey0=Ez0=0。试编写一个程序表示在区域0 设Emax是电场最大的振幅,可以得到 (6) 已知t=60 ns时在点P(0.6,0.6,0.6)处有: (7) 所以电场最大振幅为 (8) 这样一来,我们就得到了均匀平面波建模的必要条件,接下来通过具体算法对该问题进行建模仿真。算法的伪代码如下表所示: 如图7所示,我们得到沿y轴正半轴运动的均匀平面波四个不同时刻的捕捉动画,纵轴是电场大小。通过建模仿真将抽象问题具体化,生成的动态图像加强了我们对均匀平面波的理解。 (a)第一时刻 (b)第二时刻 (c) 第三时刻 (d)第四时刻图7 均匀平面波的动态过程 问题描述:在自由空间中存在一个均匀平面波,已知该均匀平面波的电场强度为E(z,t)=4.0cos(ωt-41.88z-30°)ax+9.0cos(ωt-41.88z+90°)ay,试编写一个程序来显示电场极化的动画。 首先我们可以从t=0时开始追踪z=0平面上电场的极化。从z轴正半轴向z轴负半轴看,可以看到电场在z=0平面上顺时针旋转,由于电磁波沿z轴正半轴的方向传播,且振幅不同,因此根据极化的分类,可以得到极化呈左椭圆形。接下来我们需要借助计算机的仿真软件实现电场极化的动画演示,在这里我们选择了具有强大图像可视化功能的Matlab进行动画演示,电场极化的伪代码可以表示为: 图8为捕捉极化任意时刻的动画里的四个时刻画面。图中显示的矢量即为例题中的电场。当动画运行时,该电场矢量将和我们分析的结果一样,呈顺时针旋转。电场极化的动态可视化由此实现。 (a)第一时刻 (b)第二时刻 (c)第三时刻 (d)第四时刻图8 极化的动态过程 利用电磁学的可视化仿真教学,将抽象的物理概念转化为静态或动态的直观图像来解决电磁学中的问题。这种将可视化理念和理论分析相结合的方法,可以有效提高学生的学习兴趣,使学生更深刻地理解电磁学中各种各样的物理概念,同时也丰富了教师的教学方式和方法,给电磁学理论和实验教学提供了一个新的思路。
1.2 磁场的可视化仿真



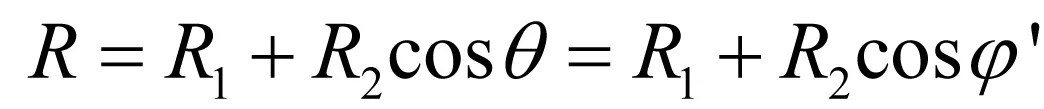




2 电磁学的动态可视化
2.1 均匀平面波的可视化

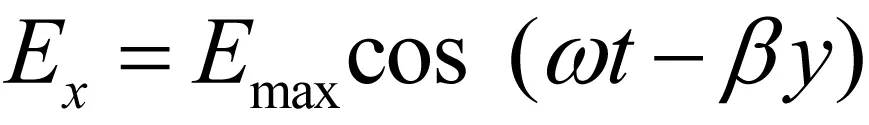

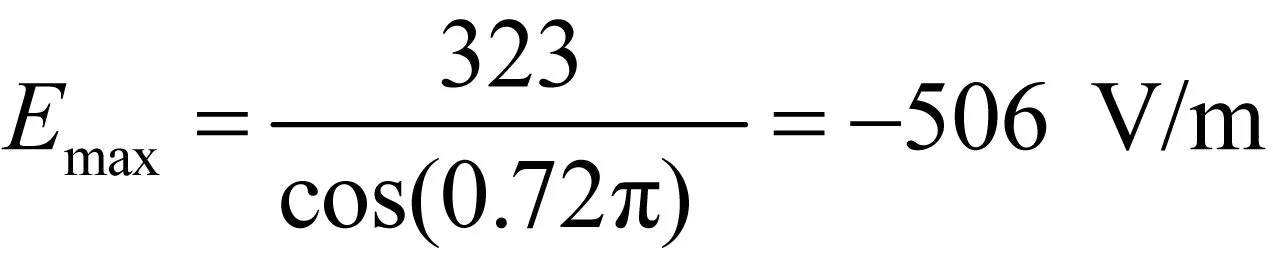


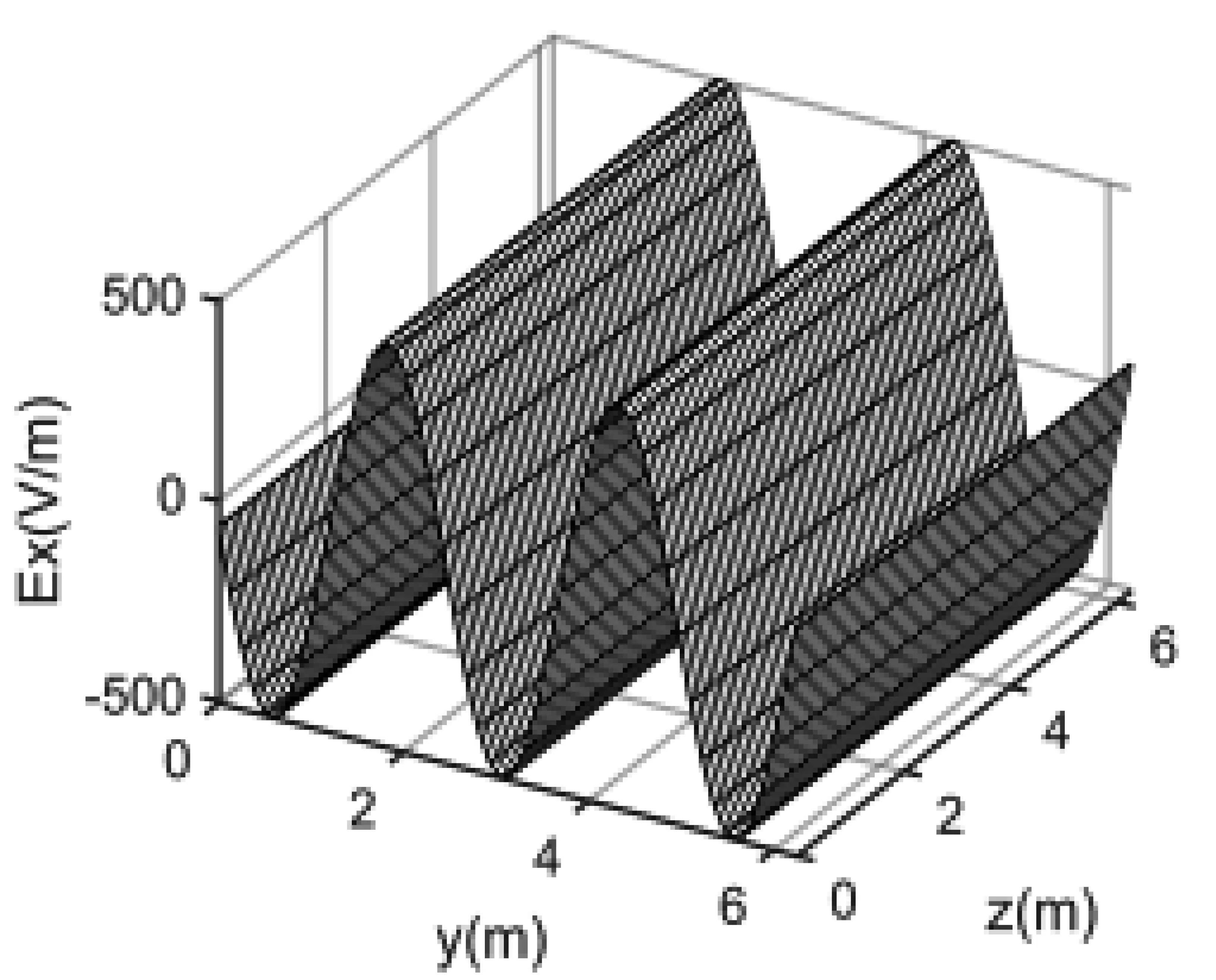
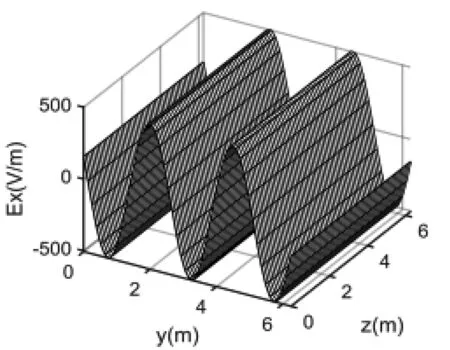

2.2 均匀平面波的极化及其可视化

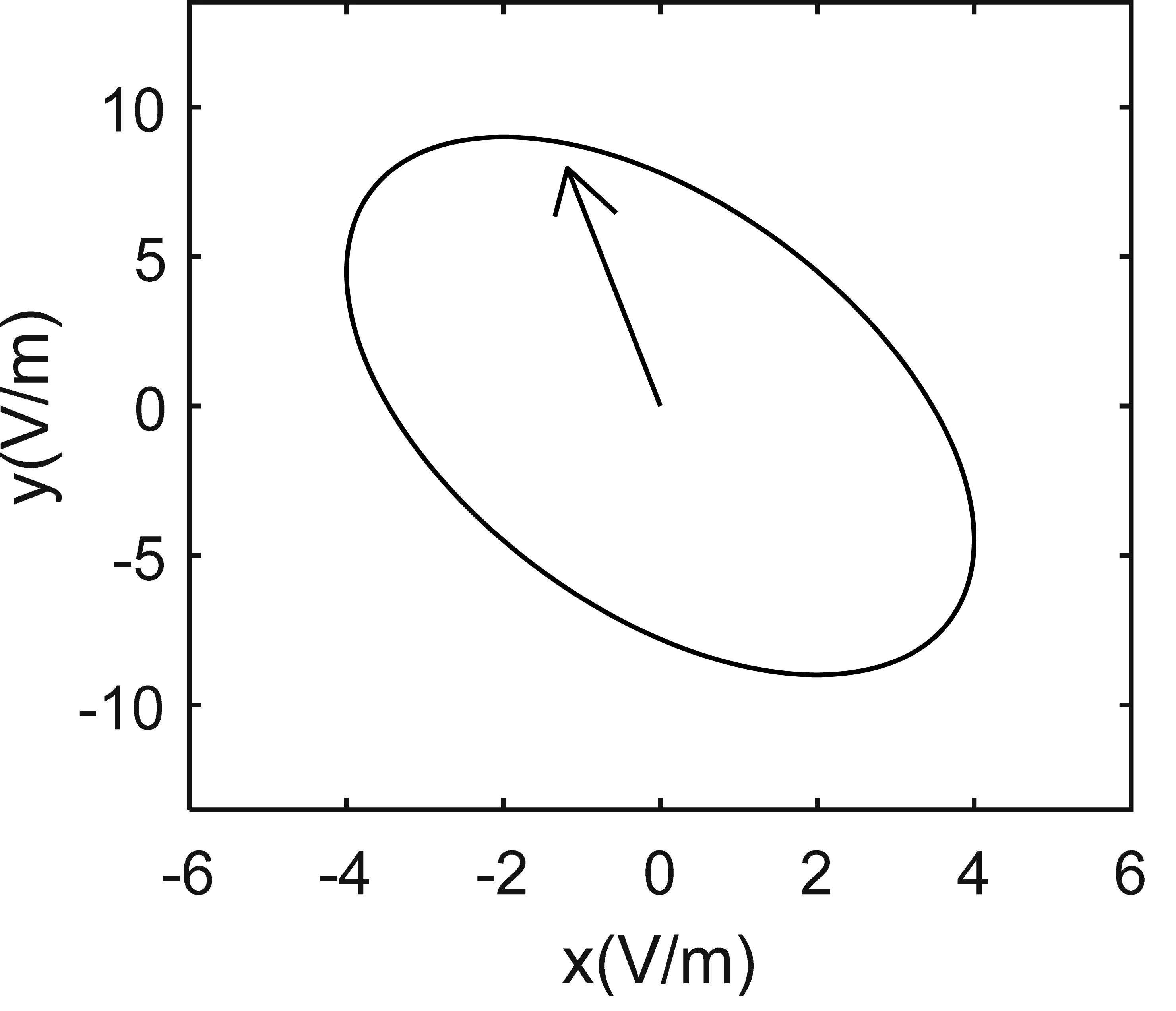



3 结语
