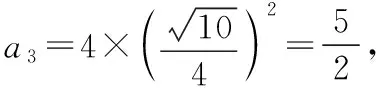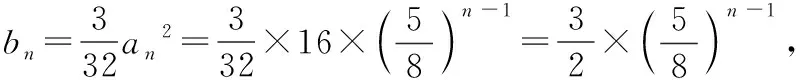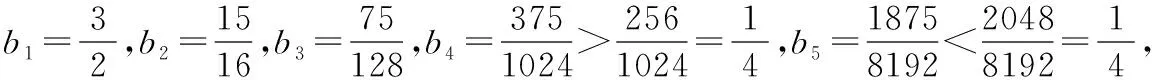高考中分类讨论思想的应用
2022-07-30江苏省张家港中等专业学校江苏张家港215600
万 丽 (江苏省张家港中等专业学校,江苏 张家港 215600)
分类讨论思想是历年高考中的重点与热点问题之一,作为一种基本逻辑思想方法,在函数、数列、圆锥曲线、导数以及创新等问题中,经常用到分类讨论思想来分析与处理,有效简化问题的研究对象,分门别类,帮助我们有条理、有逻辑地解决问题.
一、函数中的分类讨论思想
由于函数的自变量、函数值、函数图像等具有一定的条件限制,在解决一些高考函数问题时,经常利用分类讨论思想来处理,在高考试题中占有重要的位置.特别在解决一些定义域不连续、参数取值有限制、分段函数以及含参函数等问题时,经常离不开分类讨论思想的应用.

A.(-∞,-1] B.(0,+∞) C.(-1,0) D.(-∞,0)
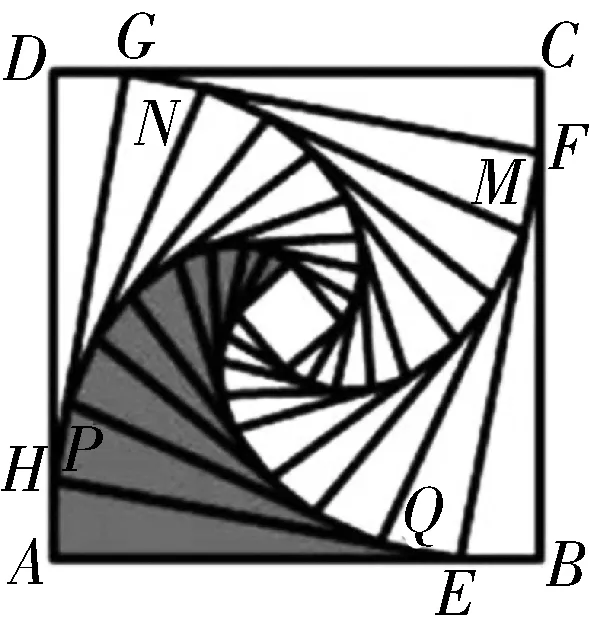
分析结合题目条件中分段函数中的定义域条件,通过对x≤-1,-1 解析根据分段函数,当x+1≤0时,即2x≤-2,此时f(x)=2-x是定义域上的减函数,结合不等式f(x+1) 当0 当x≥0时,此时条件中的不等式f(x+1) 综上分析,可知x<0,故选择答案D. 点评函数问题中的分类讨论思想,一直是高考中分类讨论思想的主阵地.涉及含有绝对值的函数问题,往往要根据绝对值取值情况来分类讨论;涉及分段函数的问题,往往要根据自变量的取值情况来分类讨论;涉及含参的函数问题,往往要根据参数的取值情况加以分类讨论等. 数列中的参数值、公式等具有一定的条件限制,特别项数还有奇偶之分以及整数要求,在具体解决问题时,经常要借助分类讨论思想,对项数、项、通项公式与前n项和公式以及对应的参数取值等情况加以合理的分类讨论,实现问题的转化与应用. A.2 B.3 C.4 D.5 分析对于给定数值所对应的数列的项问题,特别是选项中给出的数值不是太大,直接比较大小也是一种非常不错的思维方式.利用不同数列的项之间的关系,通过分类讨论,借助同开方背景下的底数大小来合理比较即可达到目的. 点评常规方法是通过构建对应的函数,利用函数的单调性来分析与应用.而借助大小比较法,通过不同项取值情况的变形与转化,分类讨论,也是一种非常不错且有效的解决方法.当然对于数值比较大,直接计算有一定难度或根本就无法计算时,这样的操作方式不可取.在高考数列问题的求解中,我们要有意识地应用分类讨论的数学思想方法去分析问题、解决问题,形成能力,提高数学素质,使自己具有数学头脑和眼光. 解三角形问题中,分类讨论的思想主要用来确定三角形的边或角不同情况下三角形的成立问题.通过分类讨论,可以考查满足条件的不同三角形问题下的边或角的相关问题. 以AB所在直线为x轴,以线段AB的中垂线为y轴,建立平面直角坐标系, 设AB=2a(a>0),A(-a,0),B(a,0),设P(x,y), 图1 点评在解三角形问题中,由于点、线、角等位置关系的变化与几何图形的直观性,往往需要根据条件加以合理的分类讨论,讨论在不同场景下解三角形的条件、公式与应用,直观流畅.同时要注意解三角形的过程中,还要根据分类讨论所产生的不同情况进行合理的批判性思考,以修正答案的真假. 在解决一些含参的函数与导数应用问题中,分类讨论思想是离不开的一种基本思想方法,借助分类讨论思想来解决单调性、参数值、极值与最值、恒成立、不等式等一些相关问题,主要是借助参数的合理分类讨论来展开与分析. 例4(2019年高考数学全国卷Ⅰ文科第20题)已知函数f(x)=2sinx-xcosx-x,f′(x)为f(x)的导数. (Ⅰ)证明:f′(x)在区间(0,π)存在唯一零点; (Ⅱ)若x∈[0,π]时,f(x)≥ax,求a的取值范围. 分析(Ⅰ)通过求导,构建函数再求导,利用导函数的正负取值情况确定单调性,结合最值并根据零点存在性定理来证明零点的唯一性; (Ⅱ)通过不等式的转化以及函数的构造,对参数进行分类讨论,并结合函数的单调性来确定不等式是否成立,从而确定参数a的取值范围. 解析(Ⅰ)由题意得f′(x)=2cosx-[cosx+x(-sinx)]-1=cosx+xsinx-1, 设g(x)=f′(x)=cosx+xsinx-1,则有g′(x)=xcosx, 所以根据零点存在性定理,可知f′(x)在区间(0,π)存在唯一零点. (Ⅱ)若x∈[0,π]时,f(x)≥ax,即f(x)-ax≥0恒成立, 设函数h(x)=f(x)-ax=2sinx-xcosx-(a+1)x, 则h′(x)=cosx+xsinx-1-a,h″(x)=xcosx=g′(x), ①当a≤-2时,h′(x)min=h′(π)=-2-a≥0,即h′(x)≥0在区间[0,π]上恒成立,则知h(x)在区间[0,π]单调递增, 则有h(x)≥h(0)=0,即f(x)-ax≥0,此时f(x)≥ax恒成立; 又h(0)=0,h(π)=-aπ≥0, 则知h(x)≥0在区间[0,π]上恒成立,即f(x)≥ax恒成立; 则知x∈[0,x2)时,h(x) 综上分析,可知a的取值范围是(-∞,0]. 点评在利用导数解决函数的单调性、极值或最值等问题时,特别是涉及参数问题,往往都离不开分类讨论思想.这里要注意参数的取值范围的界定以及合理的分类标准,在不同取值标准下,结合导函数、原函数的取值情况等加以全面、系统的分类讨论与分析,也是历年高考中都离不开的一个重要思想方法与考查热点内容. 创新问题中,借助现有的概念、运算法则和运算律等的基础上定义一种新的概念、运算、规则、性质等的问题,经常要利用创新实质加以分类讨论.特别涉及参数、关系式、不同定义要素之间等,要加以分类讨论,综合应用. 例5(2022届江苏省常熟市高三(上)阶段性抽测(二)(2021年12月)第11题)(多选题)网络流行语“内卷”,是指一类文化模式达到某种最终形态后,既没办法稳定下来,也不能转变为新的形态,只能不断地在内部变得更加复杂的现象.数学中的螺旋线可以形象地展示“内卷”这个词.螺旋线这个词来源于希腊文,原意是“旋卷”或“缠卷”,如图2所示的阴影部分就是一个美丽的旋卷型的图案,它的画法是:正方形ABCD的边长为4,取正方形ABCD各边的四等分点E,F,G,H,作第二个正方形EFGH,然后再取正方形EFGH各边的四等分点M,N,P,Q,作第三个正方形MNPQ,按此方法继续下去,就可以得到图2.设正方形ABCD的边长为a1,后续各正方形的边长依次为a2,a3,…,an,…;如图2所示的阴影部分,设直角三角形AEH面积为b1,后续各直角三角形面积依次为b2,b3,…,bn,….下列说法正确的是( ). 图2 D.数列{bn}的前n项和Sn<4 分析以创新情境来创设背景,结合平面几何图形与等比数列来合理交汇,借助各不同选项的情况,利用分类讨论思想,结合多选题的创设情境,合理分类讨论,巧妙正确判断各选项的真假情况. 故选择答案B、C、D. 点评此题是一道涉及创新场景、平面几何与数列的“新定义”问题,充分体现思维的创新性.以多选题为创新类型,从不同视角展开,巧妙通过参数的分类讨论,合理结合等比数列的概念、通项公式、求和公式以及相关的应用来展开,在考查数学基础知识的同时,也考查各方面的思想方法与数学能力. 分类讨论思想在其他一些数学基础知识层面也是经常碰到的,关键就是抓住条件中相关的参数等方面的信息,合理制订分类标准,逐个分析与解决,巧妙实现“化整为零,各个击破,再积零为整”的数学策略,完美转化,巧妙解决.二、数列中的分类讨论思想



三、解三角形中的分类讨论思想




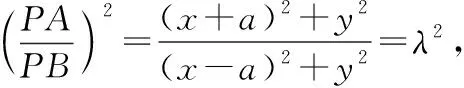







四、导数中的分类讨论思想
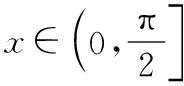



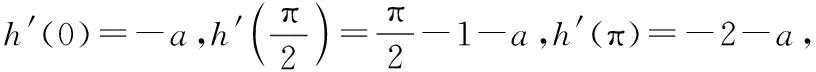

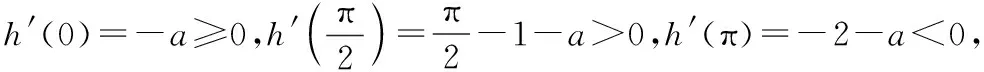
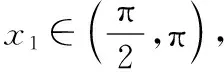




五、创新性中的分类讨论思想