基于奇异值分解的有载调压变压器故障智能检测算法

孟潇康，孙岚岚

河南开封科技传媒学院，河南 开封 475000

0 引言

有载调压变压器是变压器中的一种，可以利用电磁感应原理实现电压控制与转换，以保持电压的稳定性[1]。变压器在运行过程中会逐渐老化，若没有及时检修，可能发生故障，进而影响输配电网的电压调节能力[2]。

奇异值分解是线性代数中一种重要的矩阵分解方法，可以通过正交换获得包含奇异值的个数和位置。应用奇异值分解技术，能够提高有载调压变压器故障智能检测算法的检测性能。

1 有载调压变压器故障智能检测算法设计

1.1 设置有载调压变压器故障智能检测标准

将有载调压变压器内部故障归纳成机械故障、电故障和热故障三种类型。其中，机械故障的检测目标是变压器的运行振动信号，不同类型的故障对应的振动频率和幅度不同，电故障可以通过设置放电电流和电压，得出有载调压变压器故障检测的比对标准[3]。

以有载调压开关滑档故障为例，该类型故障是指挡位指示不停改变，极易引发开关故障，损坏变压器。连贯调整挡位依赖机械轴带动滑块断开开关，等价于滑动器，其断开开关的时间为30 ms，只有在此过程中触点断开，电动机才能停止转动。若带载的调压开关滑挡不能正常断开，接触器一直有电流，电动机运行回路总处于带电状态，会导致电动机无法停止运转，此时认为变压器设备处于故障状态。当行程开关正常工作时，若两个接触器之间有剩余磁，则行程开关断开后接触器不能恢复，应及时更换接触器，故障即可排除。此外，变压器局部放电故障初期属于低能量放电，由于各种因素的综合作用，有可能发展成高能放电[4]。同理可以得出所有故障类型的运行特征，并将其以量化特征的形式标注。

1.2 建立有载调压变压器等效模型

有载调压变压器由分接开关、驱动单元、检测单元和控制单元四部分组成，在等效电路结构中，检测器一次侧与变压器的次级侧电压相连；二次侧与直流电源电路供电相连，同时为过零检测电路和电压测量电路提供电压模拟信号[5]。控制单元由直流电源、单片机、控制信号输出及启动机构控制等部分组成，在为其他组件提供电力支持的同时，控制各元件的运行模式。

假设有载调压变压器在工作状态下，高压侧电压和二次侧额定电压分别为U1和U2，则存在如下关系式：

式中：ΔUt和k分别为一次侧的变压器电压损耗和变压器的变比，两个变量的计算公式如下：

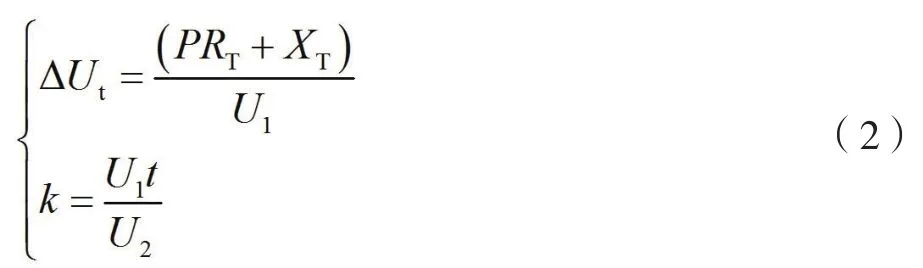
式中：P为变压器的运行功率；RT和XT分别为变压器的电阻值和电抗值；t为设备的运行时长。将式（1）与式（2）联立，可以得出一次侧分接开关电压。

带载调压变压器可以在不切断负荷电流的情况下自动切换，比较实际采集的电压值与额定电压，通过自动调压系统控制发出相应的控制命令，自动完成有载调压，从而将电压调节到合格范围内。结合有载调压配电变压器的组成结构及电压调节工作原理，完成等效模型的建立。

1.3 利用奇异值分解技术提取信号故障特征

对于一个包含周期成分的信号，对其构建的矩阵进行奇异值分解后，奇异值的最大值反映了此主要周期成分的大小。对于一个弱噪声信号，第二个奇异值会变得很小，整个奇异值比谱的值变得很大，从而实现周期性信号的特征检测[6]。

将具有时间规律的变压器运行数据构建为矩阵形式，用于奇异值分解处理。构建的矩阵标记为X。利用式（3）对变压器运行信号数据进行奇异值分解：

式中：Hm和VnT分别为m阶正交阵和n阶正交阵；S为对应数据的非零特征值，可以表示为

式中：H为矩阵的非零主量奇异矩阵；σ1，…，σk分别为序列信号的第1～k个特征值。

由式（4）可以得出由σ1，…，σk组成的特征值序列。在实际的故障提取中，以有载调压变压器的电流信号为例，将电源频率分量分解成奇异值对应的子空间，将其他频率分量分解到后续子空间中。选择第二个到最后一个子空间进行重构，提取信号中的故障特征分量，提取结果可以表示为

式中：σI为信号特征提取分量；Hi为离散点在周期性信号中拥有较强表现的特征值；ViT为周期信号的奇异值矩阵；i为周期信号的序列；βi和P分别为分解子空间及其数量。同理，通过奇异值分解技术，将有载调压变压器运行信号中的机械振动频率、电压等数据分解到不同的子空间中，按照上述流程可以有选择地提取特征分量。

2 检测性能测试实验

2.1 实验过程

2.1.1 设置有载调压变压器与运行数据样本采集方法

试验现场选在某地区7座变电站，试验共检测200台不同电压等级、不同负荷的有载调压变压器，在初始状态下选择的变压器均为无故障设备。为了保证实验的研究意义，采用人为破坏的方式将170台变压器调整为故障状态，并采集600组不同类型的信号资料进行对比分析[7]。同理可以得出其他样本设备的机械振动信号、电流信号及电压信号的收集结果。

实验的研究对象均为型号为SFZ9-50000/135的有载调压变压器，其额定容量为6 300 kVA，额定电压及分接范围为35 000 kV±3×2.5%，高压侧和低压侧的额定电压分别为280 kV和2 844 kV，工作频率为50 Hz。将选择的有载调压变压器连接到实验环境中，并与电网线路相连，将研究对象调整为工作状态。在数据样本采集过程中，为了尽量避免非检测设备产生的干扰，采用多种测试手段对原始信号进行数据采集。此外，由于变压器体积较大，需要对变压器不同的位置进行测试，以获取更全面的运行信号资料。通过对试验信号的分析，观察其固有特征量，将准备的变压器研究对象平均分为5个组别，每个组别包含40台有载调压变压器设备，但故障设备数量不固定，可以通过对破坏设备的标记与统计，确定各个组别中的故障设备数量，以此作为验证故障检测结果正确性的比对标准[8]。

2.1.2 设置实验工况

与普通变压器相比，有载调压变压器在工作过程中会根据不同的荷载情况调整其运行方式，因此在实验中设置两种工况：阻感性负载条件下的调压；阻性负载下的调压，并记录两种不同负载工况下的电压调整过程，如表1所示。

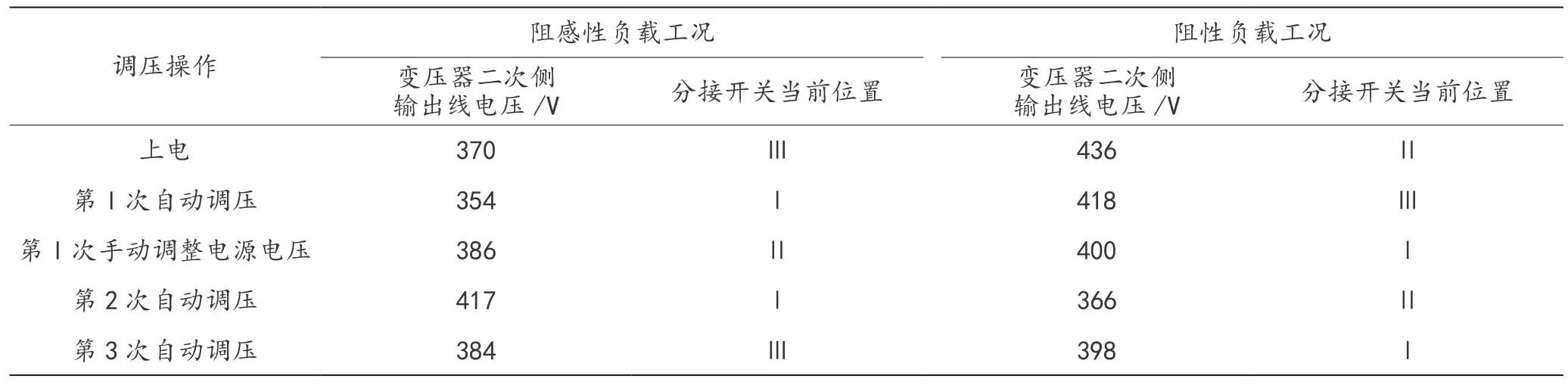
表1 变压器调压操作结果

在上述工况下，将变压器设备的实时运行数据代入设计的故障智能检测算法中，得出最终的故障检测结果。同理可以得出实验中其他设备对象的故障检测结果，通过与实验设置信息的比对，可以确定当前故障检测结果是否正确。

2.1.3 设置检测性能测试指标

实验分别从检测精度和时效两个方面进行测试。其中，故障检测精度的量化测试指标为误检率ηerr和漏检率ηloss，其计算式为

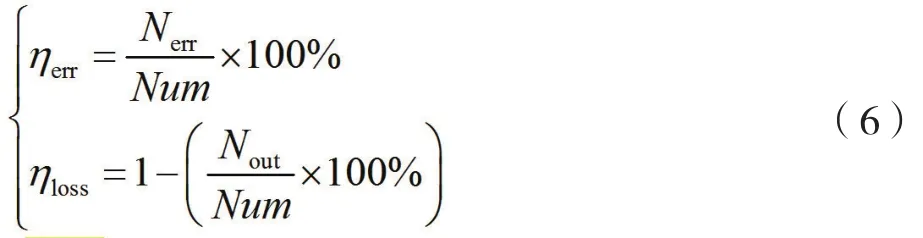
式中：Nerr、Nout和Num分别为故障检测错误、正常检测输出及变压器样本的数量。

在故障检测错误的判定过程中，需要考虑故障点的定位结果。计算得出ηerr和ηloss的值越大，说明设计算法的检测精度越低。为了保证故障算法的应用价值，要求设计算法的误检率、漏检率均不得高于2%。

检测时效性能时，设置的量化测试指标为检测算法运行时间，可以通过调取检测算法运行环境后台数据直接得到，设置检测算法的运行最大时间为3.0 s。

2.2 实验结果

在两种工况下，通过收集相关数据，得出反映设计算法检测精度的测试结果，如表2所示。

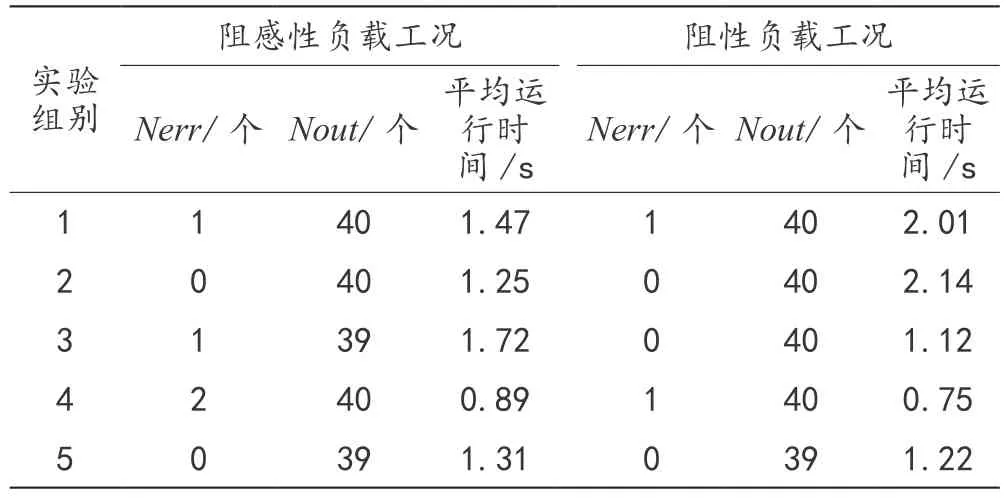
表2 检测精度测试结果统计表

将表2中的数据代入式（6），可以得出设计检测算法的平均误检率和平均漏检率分别为1.50%和0.75%，均低于2%。综合上述两种工况，设计算法在检测精度方面满足设计与应用要求。

在检测时效方面，设计检测算法的平均运行时间为1.39 s，低于3.00 s，具有较高的检测时效性。

3 结束语

在新能源快速发展的背景下，有载调压变压器的相关企业抢占市场领域，扩大业务范围，推动了变压器设备的结构优化与创新。应用奇异值分解技术，可以提高有载调压变压器故障智能检测算法的检测性能，对于维护变压器乃至电网系统的稳定与安全具有重要意义。然而，受到时间和空间的限制，文章的实验只考虑了变压器阻感性负载和阻性负载两种工况，未考虑空载等其他调压情况，因此最终得出的实验结果存在一定的局限性。针对上述问题，还需要在今后的工作中进一步补充和优化。