马尔科夫链在溧阳市降水量预测中的应用

2022-07-29林小明胡尊乐纪小敏

江苏水利 2022年7期

林小明，华晨，胡尊乐，李丹，闫浩，纪小敏

（1.溧阳市水利局，江苏常州 213300；2.江苏省水文水资源勘测局常州分局，江苏常州 213022；3.江苏省水文水资源勘测局，江苏南京 210029）

溧阳市地处北亚热带边缘、太湖流域上游，境内地形变化较大，山圩紧依，河流源短流急，水情盈枯强弱多变。进入20世纪80年代以后，一方面随着溧阳市工业化和城镇化的迅速发展，水资源短缺问题日趋突出；另一方面因流域下垫面及上下游工情变化较大，区域防洪压力有加重之势。准确预测区域年度降水量，合理配置水资源，减缓水资源供需矛盾，为区域防洪提供可靠的技术支撑显得较为迫切且具有重要的社会经济效益［1］。

本文对溧阳市1951—2020年的降水量进行分级，将其分为枯水年、偏枯年、平水年、偏丰年、丰水年5个状态，以马尔科夫链理论［2-3］和模糊集理论［4］为基础，以规范化的各阶自相关系数为权重，建立适用于溧阳市降水量的马尔科夫链加权预测模型，对溧阳市2021年的降水量、丰枯水重现期进行了预测，旨在为溧阳市水旱灾害防御、水资源优化配置以及河湖生态流量的调度提供技术支撑。

1 基本原理与步骤

1.1 马尔科夫链

马尔科夫链是研究事物状态及状态转移规律的理论，通过不同状态的初始概率及状态的转移概率来确定状态之间的变化趋势，从而预测其未来变化趋势的一种技术，其基本原理如下。

如果对时间t的任意n个数值（n≥3），在条件X（ti）=xi（i=1，2，…，n-1）下，X（tm）的分布函数恰好等于在条件X（tn-1）=xn-1下X（tn）的分布函数，即：

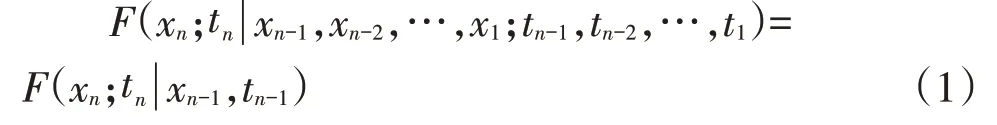
通常称X（tn）为马尔可夫链（过程），马尔科夫链法可用来预测未来发生状态的水文时间序列，广泛用于一个区域中长期降水量的预测预报。

从应用的实践来看，传统的马尔科夫模型采用最大隶属原则来确定预报对象的状态，它有两大缺点：一是只考虑最大概率，忽略了其他概率的影响；二是无法预报对象的具体值，只能预报对象所在的区间。而加权马尔科夫链预测模型［5-7］先依据前面若干时段的预报对象对后面某一时段的预测对象进行预测，再考虑前面各个时段与所求时段的相关关系进行加权求和，其最大优点是既考虑最大概率的影响，也考虑其他概率的影响，弥补了传统的马尔科夫模型的不足，提高了预测的可靠性。

1.2 模糊集理论中的级别特征值

模糊集理论是一种描述模糊现象的方法，它把待考察的对象及反映它的模糊概念作为一定的模糊集合，建立适当的隶属函数，通过模糊集合的有关运算和变换，对模糊对象进行分析。具体到前述马尔科夫链中的预测对象，就是通过模糊集理论中的级别特征值［8］解决传统马尔科夫链中“最大隶属原则”只考虑最大概率影响的问题，而兼顾考虑其他概率的影响，也就是通过级别特征值对马尔科夫链中的各状态赋予相应权重，亦即加权马尔科夫链。

（1）对各状态赋予相应权重，得权重集w={w1，w2，…，wi}，其中i为研究系统的状态。权重公式为

式中：η为最大概率作用指数，指数越大越能够突出最大概率的作用，本文取2；p i为状态i的概率。

（2）对各级别特征值进行计算，级别特征值H计算式为

若级别特征值H＞i，则预测对象的特征值Q为

若级别特征值H＜i，则预测对象的特征值Q为

式中：Ti、Bi分别为状态区间的上限和下限。

1.3 加权马尔科夫链法计算步骤

以均值、方差作为选取预测对象（Q）组合的准则，即既定组合方差下的最大均值或既定均值下的最小方差。

（1）计算预测对象的均值和方差S，建立指标值分级标准，确定序列中各个时段的指标值所处的状态。计算式为

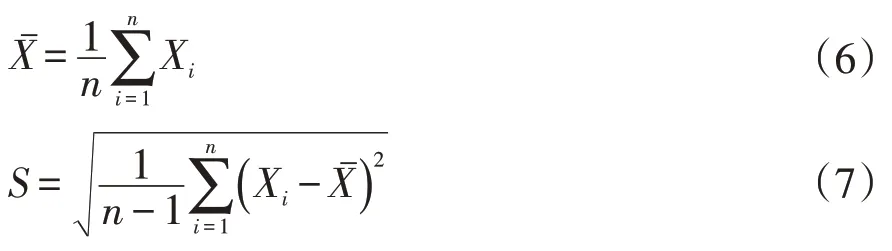
（2）对预测对象的序列进行马氏性检验。检验随机过程是否具有马尔科夫性［9］是应用马尔科夫预测模型的必要前提。一般情况下，选用离散序列的马尔可夫链来对变量具有随机性的序列进行“马氏性”检验，检验常用χ2（卡方分布）统计量。计算方法为：

设研究的序列状态个数为m，使用()f ij，i、j∈I表示转移频数概率矩阵，把各个列之和去除以全部元素之和，就会得到“边际概率”，用字母pj表示，其中：

当m很大时，χ2（卡方分布）统计量为

如果给定显著性水平为α，经查表可得值。如果，则拒绝零假设，可以认为序列具备“马氏性”，反之则这个序列不能当作马尔可夫链来对待。

（3）计算各阶自相关系数。计算式为

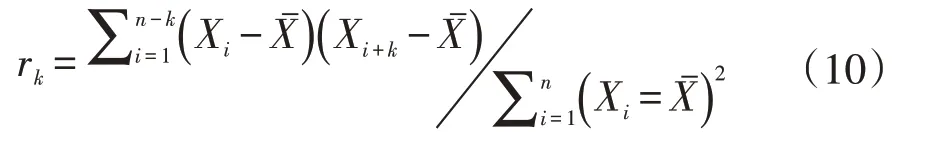
（4）考虑到各阶相关系数可能会出现负值，需对各阶自相关系数进行规范化处理，即：

式中，m为预测时需要计算的最大阶数。

（5）对上述步骤的结果进行统计，得到不同步长的状态转移概率矩阵。以前面各年预测对象为初始状态，结合其相应的状态转移概率矩阵即可预测出该时段预测对象状态，其中k为步长。

（6）指标值处于某状态的预测概率可用处于此状态的各预测概率的加权和Pi表示，max(P i,i∈I（)I为状态空间）对应的状态即为此时段指标值的预测状态。然后，利用模糊集理论中的级别特征值即可计算出此时段的预测值（Q）。重复以上步骤可预测下一时段的预测值。

（7）进一步对加权马尔科夫链的遍历性、平稳分布进行预测。其中，遍历性是指对于有限状态马氏链，如果存在正整数s，并且对所有的i，都有j=1，2，…，k对于成立，则该马氏链必具有遍历性。平稳分布是指对于有限状态马氏链，这个链的所有状态都是正常返的，且这是极限分布Pj是唯一的平稳分布［10］。马尔科夫链的遍历性、平稳分布预测是采用加权马尔科夫链法的必要条件。

2 应用实例

本文选取江苏省溧阳市1951—2020年降水量作为对象，采用上述加权马尔科夫链法对该市2021年降水量及丰枯年重现期进行预测分析。

2.1 均值与方差

利用式（6）、式（7），计算出溧阳市1951—2020年平均降水量=1 165.6 mm，均方差S=246.1 mm。

2.2 分级与状态

（1）根据水文上传统的年型分级定义，用均方差法把溧阳市1951—2020年降水量分成干旱年、偏旱年、平水年、偏丰年、丰水年等5级（状态）。其中，干旱年定义为，偏旱年定义为平水年定义为，偏丰年定义为，丰水年定义为，见表1。

（2）根据已知的溧阳市年降水量序列，结合表1的分级标准，判断每年降水量的状态，见表2。

表1 溧阳市降水量分级

2.3 马氏性检验

利用式（8）、式（9），对溧阳市年降水量序列进行马氏性检验。其中，状态空间m=5，显著性水平则拒绝零假设，可以认为溧阳市年降水量序列具备“马氏性”。

2.4 成果预测

（1）利用式（10）和式（11），计算出前5阶自相关系数rk与相应的权重Wk，见表3。

表3 溧阳市年降水量1～5阶各阶自相关系数及权重

（2）根据表2，计算溧阳市1951—2020年降水量各种步长的状态概率矩阵，见式（12）。

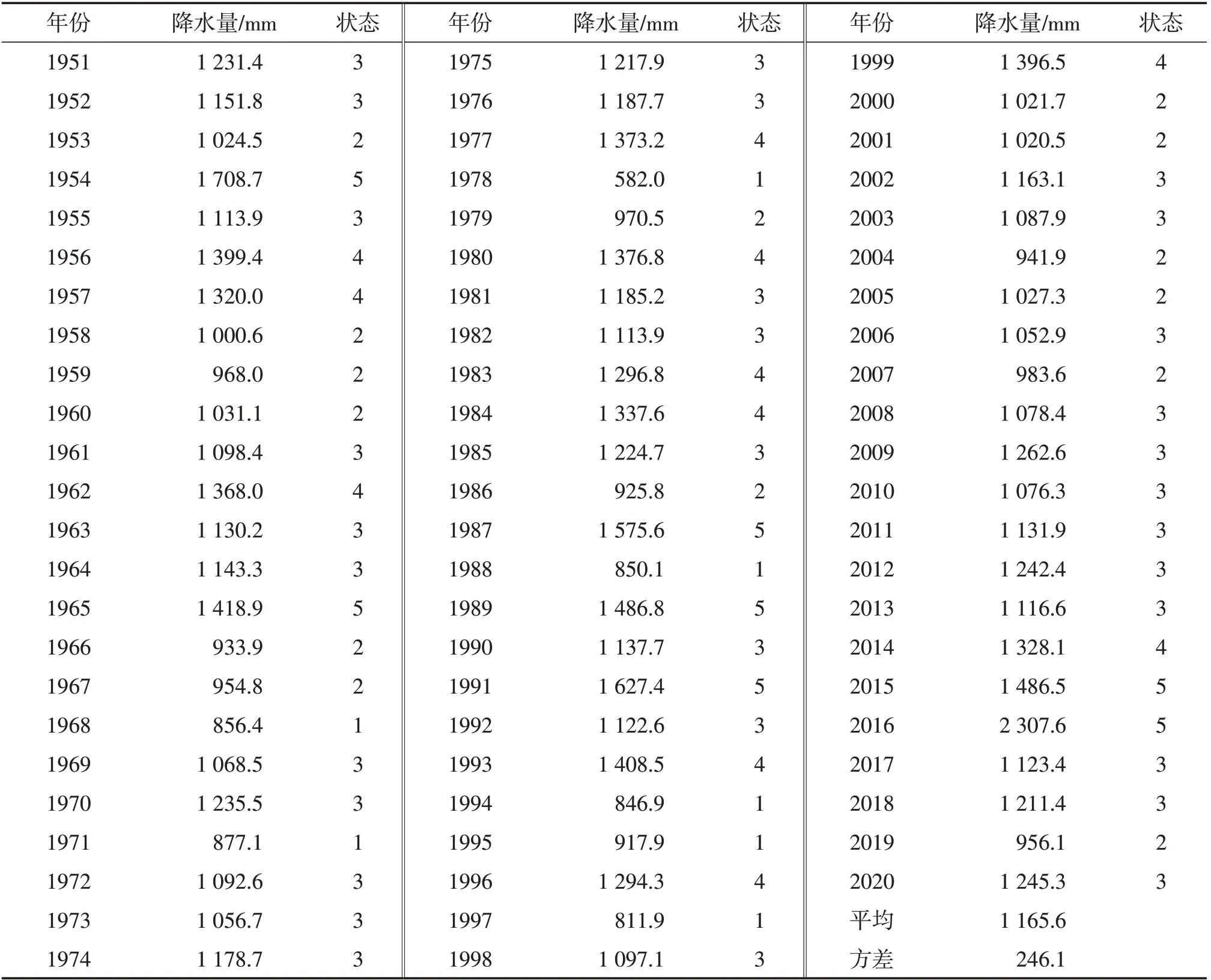
表2 溧阳市年降水量序列及状态

（3）根据溧阳市1951—2020年降水量及其相应的状态转移概率矩阵，采用1～5阶权重系数对溧阳市2021年的降水量状态进行预测，结果见表4。

各状态对应的加权和分别为0.0469、0.2686、0.0664、0.0488、0.5693。由表4可知，max{ }

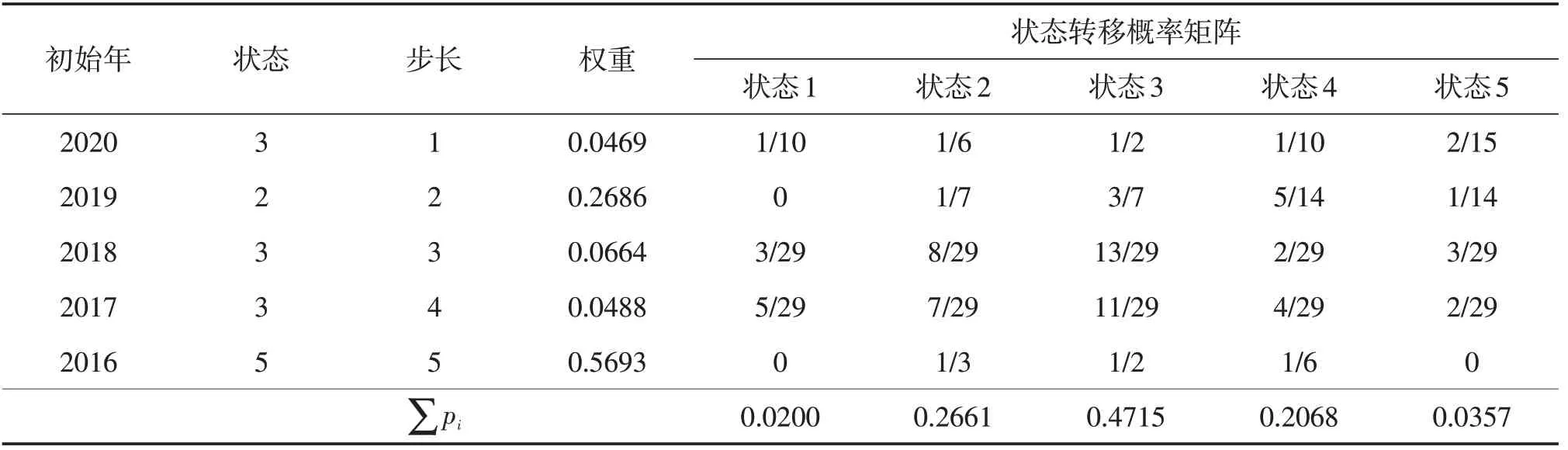
表4 溧阳市2021年降水量预测

p i,i∈E=0.4715，对应的i=3，即溧阳市2021年降水量预测状态为3（平水年），状态3的数值区间为［1 042.6，1 288.7］。由模糊集理论计算得级别特征值H=3.825，H＞i，故由式（4）计算得2021年降水量为1 408.4 mm，实测值为1 464.5 mm，相对误差为-3.8%，符合相关标准（≤±20%）要求。