对一道共振习题引发问题的探讨

杨钧捷

(江苏省海门中学 江苏 南通 226100)

1 问题引入

在一次习题教学中笔者讲述了这样一道习题，题目如下.

【例题】如图1所示，球a振动后，通过水平细绳迫使b和c振动，下列说法中正确的是( )

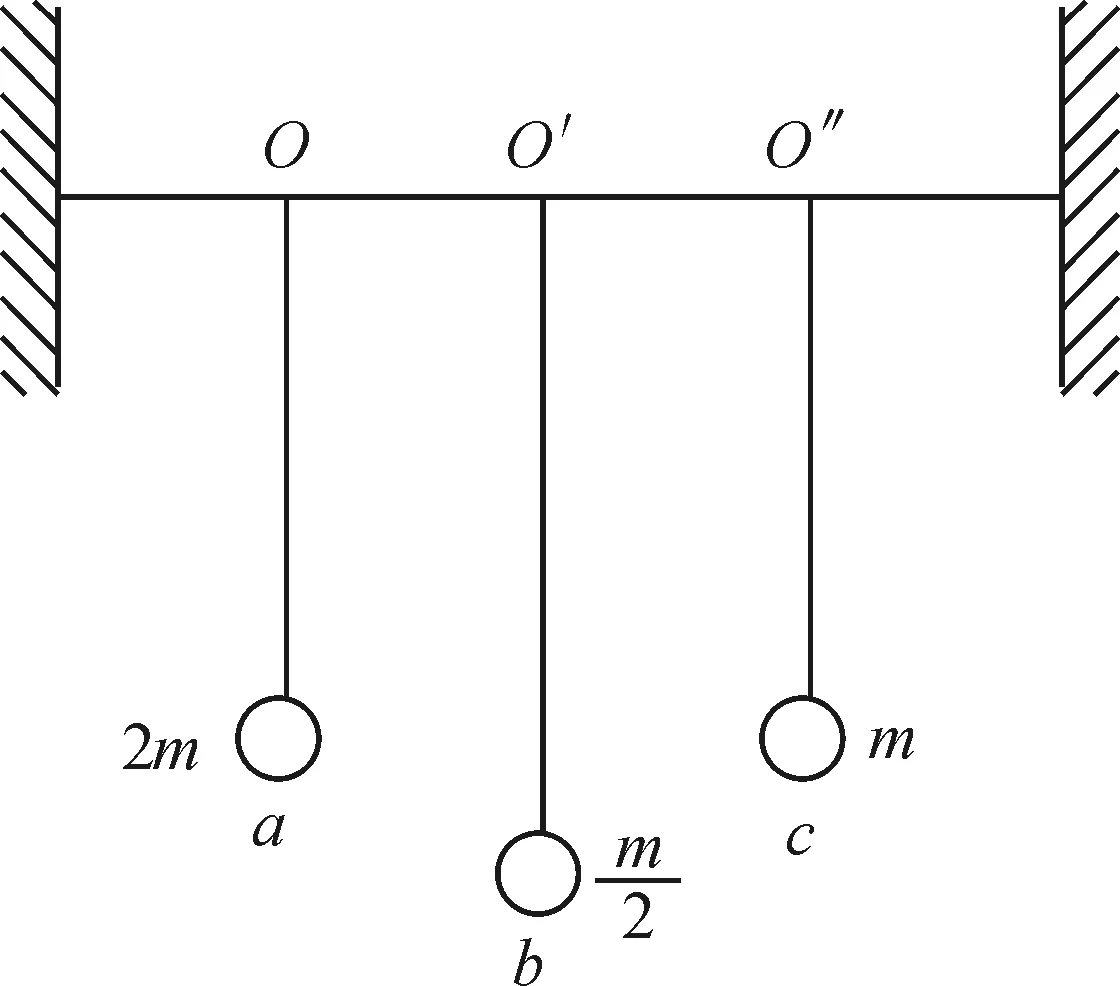
图1 例题题图

A.只有球a和球c振动周期相等

B. 球c的振幅比球b小

C. 球c的振幅比球b大

D. 球a,球b,球c的振动周期不等

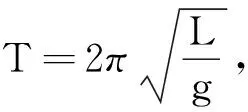
教辅资料中给出的参考答案是： 球a振动充当驱动球，b和c两球的振动周期都应当等于球a的振动周期，所以A和D错误.球c的摆长与球a的摆长相同，周期也相同，所以球c做受迫振动的振幅大，B错误，C正确.

教学中学生提出这样一个问题，球b虽然不能产生共振，但它的质量小，道理上它的振动更“容易”，这样，会不会导致其振幅比球c共振时的振幅还要大呢？这个问题同时也引发笔者思考，在周期性驱动力作用下，单摆的振幅与质量到底有些什么关系？鉴于此问题对于中学命制此类试题有一定价值和意义，为此，本文尝试在此作出深入探讨.

2 问题探讨

2.1 建立模型

球b提供驱动力，认为b和c两球都受到相同的驱动力，则

F=F0cosωt

其中,F0是驱动力的幅值，ω是驱动力的角频率，单摆在回复力和驱动力的作用下，根据牛顿第二定律

其中,m为摆球质量，l为摆长,用微分方程表示为

求解可得，当振动稳定下来后，单摆位移随时间的变化关系为

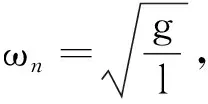
2.2 分析结果

就本文前述习题而言，球b虽然质量小，其振幅会有所增加，但由于球c发生了共振，从理论上讲，其振幅可以接近无穷大，所以球c的振幅一定是最大.

2.3 拓展与讨论

实际实验中，我们观察到共振时，单摆的周期并不是无穷大[1].这主要是因为存在阻尼作用，如果考虑这个因素，单摆的运动方程变为

求解微分方程可得，当振动稳定下来后，单摆位移随时间变化情况满足

易得，球b受迫振动的振幅为

同理，球c受迫振动的振幅为

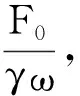
3 结束语

本文从振动微分方程求解的角度，证明了摆球质量确实会影响受迫振动振幅，但无论是否考虑阻尼影响，质量是否相同，共振的振幅是大于其他情况的.此探讨主要是为了便于教师从本质上更好理解受迫振动和共振，从另一个角度思考此类力学问题.

致谢

本文撰写过程中得到昆明市五华区教育体育局副局长、五华区基础教育发展研究院赵坚老师的悉心指导.