基于联系熵的工科专业课成绩分析及评价*——以“光电信息物理基础”为例

朱月红 郑一博

(河北地质大学光电技术研究所 河北 石家庄 050031；河北省光电信息与地球探测技术重点实验室 河北 石家庄 050031)

朱占龙

(河北省光电信息与地球探测技术重点实验室 河北 石家庄 050031;河北地质大学信息工程学院 河北 石家庄 050031)

唐雪雷 潘媛媛

(河北地质大学信息工程学院 河北 石家庄 050031)

王 远 杨清莲

(河北地质大学光电技术研究所 河北 石家庄 050031；河北省光电信息与地球探测技术重点实验室 河北 石家庄 050031)

赵克勤提出集对分析(Set Pair Analysis，简写为SPA)，将其作为一种系统分析方法，同时结合熵的概念提出联系熵，将系统的确定性与不确定性有机结合起来，并讨论了联系熵与模糊熵、物理熵、信息熵、负熵、热力学熵的联系[1].认为联系熵是一种综合熵，其他形式的熵都可以看作是联系熵中的某个部分熵[2～4].联系熵适用于度量事件发展的有序与无序，反映集对事件的内部混乱状态，可用于风险及安全评价、教学测量与评价等.在此采用联系熵方法对工科专业的专业课成绩进行分析与评价.

1 联系熵

1.1 联系度

两个集合A和B组成集对H=(A,B)，在某个具体问题背景下，对这个集对H的特性分析，得到N个特性，其中有S个为集对H中两个集合A和B所共有，在P个特性上集合A和B相对立，在其余F=N-S-P个特性上既不相互对立，又不为两个集合共同具有，则这个集对H中两个集合A和B的联系度可以表示为[4]

μ=a+bi+cj

(1)

1.2 联系熵

联系熵由同熵Sa、异熵Sb、反熵Sc3部分构成，其定义如下[3]：

同熵Sa=∑anlnan

(2)

异熵Sb=i∑bnlnbn

(3)

反熵Sc=j∑cnlncn

(4)

联系熵S=Sa+Sb+Sc

(5)

2 成绩分析及评价

教学过程中学生每学期的每一门课程考核成绩，都有相应的成绩统计分析.学校也需要掌握每个学生的课程成绩及学习情况.成绩统计分析主要有平时成绩、期末成绩、不同分数段的人数及占比、最高分、最低分、平均分等信息.这些信息可以很直观地从成绩表中得出.

但是，班级之间在同一门课程中的差异，或同一班级在不同课程中的差异，这些信息不能从成绩表中直接得出.为科学准确地获取这些差异，现采用联系熵的方法对成绩进行分析，以获取班级之间的差异，为教学改革提供参考.

下面以光电信息科学与工程3个班为研究对象，甲、乙、丙3个班的光电信息物理基础课程成绩如表1所示，成绩分为优、中、差3档.分档标准为：分数≥80为优，60≤分数<80为中，分数<60分为差.

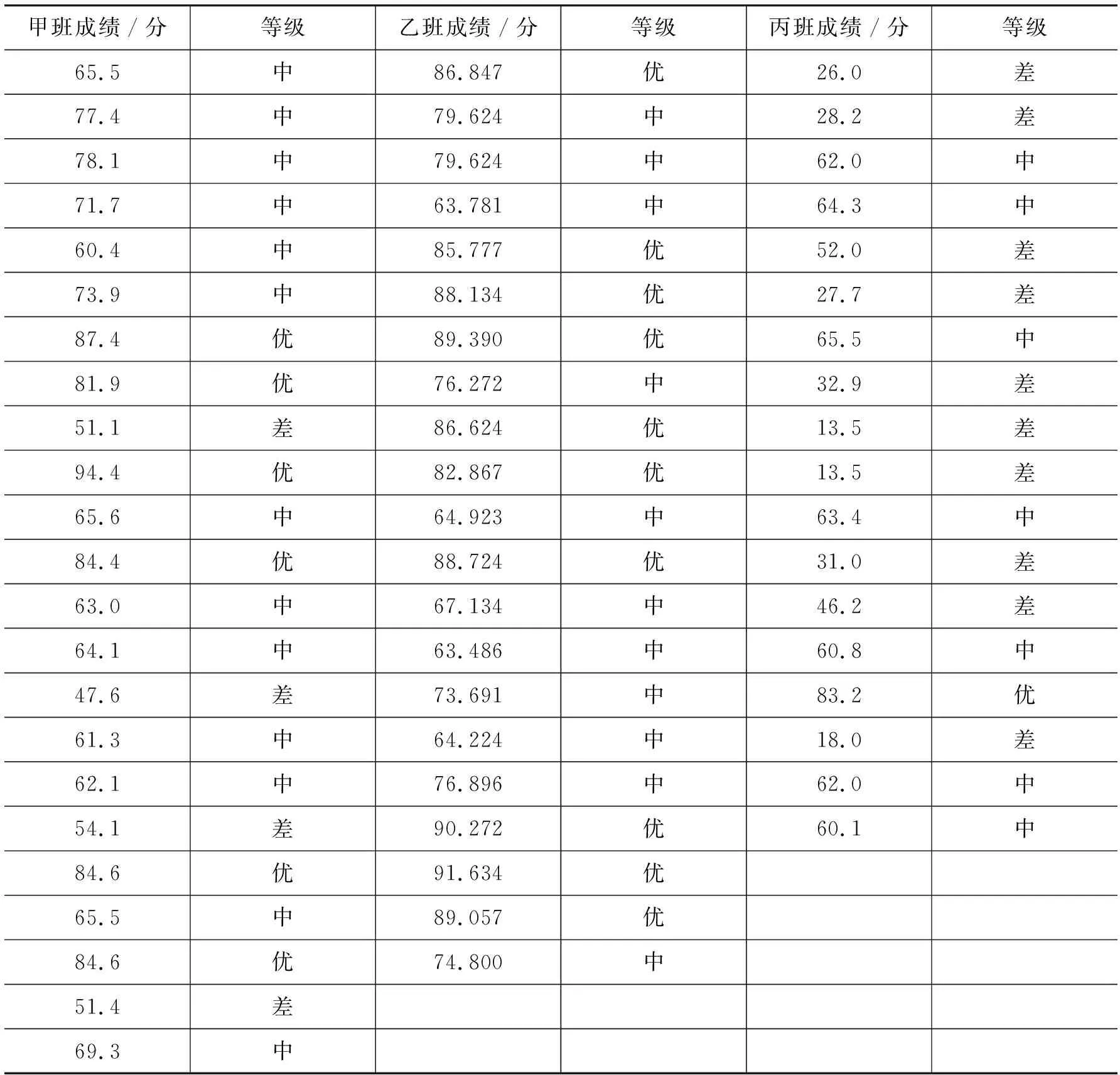
表1 甲、乙、丙3个班的光电信息物理基础课程成绩

根据上述分档标准，可得到各档占比分别为

甲班：“优”的学生数占0.26；“中”的学生数占0.57；“差”的学生数占0.17.

乙班：“优”的学生数占0.48；“中”的学生数占0.52；“差”的学生数占0.

丙班：“优”的学生数占0.06；“中”的学生数占0.39；“差”的学生数占0.55.

则甲、乙、丙3个班的学生成绩的联系度形式为

μ甲=0.26+0.57i+0.17j

(6)

μ乙=0.48+0.52i+0j

(7)

μ丙=0.06+0.39i+0.55j

(8)

μ甲,μ乙,μ丙3个联系度的平均联系度μ为

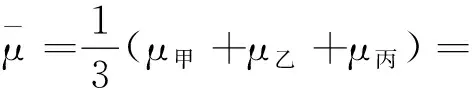
(9)

从式(6)～(9)可以得出

即丙班b值最小，乙班的b值次之，甲班的b值最大.根据集对分析理论，b值是对处于a与c之间中间事物状态的一种度量，称之为不确定性，因此,甲、乙、丙3个班学生成绩，相对来说，b值最小的丙班最稳定，b值最大的甲班最不稳定，b值介于两者之间的乙班稳定性处于两者之间.

现对甲、乙、丙3个班的学生成绩从熵的角度进行描述和分析.根据式(2)～(5)可得

同熵Sa=∑anlnan=-0.871 35

(10)

异熵Sb=i∑bnlnbn=-1.027 68i

(11)

反熵Sc=j∑cnlncn=-0.630 04j

(12)

总联系熵S总=Sa+Sb+Sc=

-0.871 35-1.027 68i-0.630 04j

(13)

相应的甲、乙、丙3个班的学生成绩的联系熵S甲，S乙，S丙分别为

S甲=0.26ln 0.26+i0.57ln 0.57+j0.17ln 0.17=
-0.350 24-i0.320 41-j0.301 23

(14)

S乙=0.48ln 0.48+i0.52ln 0.52+0j=

-0.352 31-i0.340 04-0j

(15)

S丙=0.06ln 0.06+i0.39ln 0.39+j0.55ln 0.55=
-0.168 8-i0.367 23-j0.328 81

(16)

为比较式(13)～(16)这4式的计算结果，从式(6)～(9)中，根据i的比例取值法[3]，令i=0.27，则

S总=-0.871 35-0.277 47+0.630 04=

-0.518 78

(17)

S甲=-0.350 24-0.086 51+0.301 23=

-0.135 52

(18)

S乙=-0.352 31-0.091 81+0=

-0.444 12

(19)

S丙=-0.168 8-0.099 15+0.328 81=

0.060 854

(20)

可以看出S总=S甲+S乙+S丙，满足式(13).甲、乙、丙3个班的平均熵

(21)

从式(18)～(21)可以看出

乙班的联系熵最小，丙班的联系熵最大，甲班的联系熵介于二者之间.结合甲、乙、丙班3个班的b值大小比较，可以看到丙班的b值最小，其稳定性最高，整体成绩最差，联系熵最大.乙班的联系熵最小，整体成绩最好，但其b值介于甲班和丙班之间，说明其稳定性不是最好.甲班的b值最大，其稳定性最差，其联系熵介于丙班和乙班之间，成绩也位于二者之间.

3 结论

采用联系熵方法对学生成绩进行了分析与评价.通过对光电信息科学与工程专业的甲、乙、丙3个班的同一门课程成绩进行分析，显示丙班成绩最差，其联系熵最大，b值最小，稳定性最好；乙班成绩最好，其联系熵最小，b值居中，稳定性也居中；甲班成绩居中，其联系熵居中，b值最大，稳定性最差.从这个结论可以看出，成绩最好的班级，其联系熵最小.成绩最差的班级，其联系熵最大，成绩的提高与联系熵的减小方向一致，这与熵增原理相吻合，说明该方法可以分析学生成绩[5].