Optimization Analysis of the Mixing Chamber and Diffuser of Ejector Based on Fano Flow Model

Lixing Zheng,Weibo Wang,Yiyan Zhang,Lingmei Wang and Wei Lu

1School of Electric Power,Civil Engineering and Architecture,Shanxi University,Taiyuan,030006,China

2School of Mechanical Engineering,Guangxi University,Nanning,530004,China

3Wind Turbine Monitoring and Diagnosis,NTRC of Shanxi Province,Taiyuan,030006,China

ABSTRACT An improved model to calculate the length of the mixing chamber of the ejector was proposed on the basis of the Fano flow model,and a method to optimize the structures of the mixing chamber and diffuser of the ejector was put forward.The accuracy of the model was verified by comparing the theoretical results calculated using the model to experimental data reported in literature.Variations in the length of the mixing chamber Lm and length of the diffuser Ld with respect to variations in the outlet temperature of the ejector Tc,outlet pressure of the ejector pc,and the expansion ratio of the pressure of the primary flow to that of the secondary flow pg/pe were investigated.Moreover,variations in Lm and Ld with respect to variations in the ratio of the diameter of the throat of the motive nozzle to the diameter of the mixing chamber dg0/dc3 and ratio of the outlet diameter of the diffuser to the diameter of the mixing chamber dc/dc3 were investigated.The distribution of flow fields in the ejector was simulated.Increasing Lm and dc3 reduced Tc and pc.Moreover,reducing pg/pe or dg0/dc3 reduced Tc and pc.The length of the mixed section Lm2,which was determined on the basis of the Fano flow model,increased as pg increased and decreased as dc3 increased.The mixing length Lm1,which was considered the primary flow expansion,showed the opposite trend with that of Lm2.Moreover,Ld increased as pg/pe and dc/dc3 increased.When the value of dc was 1.8 to 2.0 times as high as that of dc3,the semi-cone angle of the diffuser ranged between 6°and 12°.At a constant dc/dc3,decreasing Tc and pc increased Ld.

KEYWORDS Mixing chamber;length;Fano flow;diffuser;diameter ratio;expansion ratio;optimization method

Nomenclature

Greek symbols

Subscripts

1 Introduction

Compared to conventional mechanical supercharging equipment (compressors, pumps, and blowers), ejectors have lower energy consumption and a simpler structure.Ejectors have been used in the refrigeration system to recover the energy of the high-pressure fluid and reduce the power of the compressor to improve the circulation efficiency of the system[1].In addition,ejectors have been widely used in the nuclear industry [2], chemical industry [3], aerospace industry [4], thermal-power generation[5],and food drying[6].

Nevertheless,the flow characteristic of the ejector is complicated due to non-equilibrium,entrainment,condensation,collision,and friction.Many scholars have carried out steady-state simulations,computational fluid dynamic(CFD)analyses,and experimental tests to investigate the performance of the ejector.Especially, CFD-based simulation and analysis can provide detailed information on the flow field[7].Peng et al.[8]built a three-dimensional CFD model to analyze the influence of the distance of the standoff from the nozzle outlet on the performance of a high-speed rotating water ejector.Wang et al.[9] proposed a control method to reduce non-equilibrium condensation in the motive nozzle of the ejector.Yang et al.[10] used a CFD model to investigate the non-equilibrium condensation of steam in the supersonic ejector.An accurate analysis of a non-equilibrium flow can optimize the motive nozzle of the ejector.Moreover, except for understanding the local flow characteristic,the whole flow properties of ejector are more necessary and important.Wu et al.[11]used a CFD model to analyze the effects of the following parameters on the distribution of flow fields in the ejector:the diameter of the outlet of the motive nozzle,position of the nozzle exit(NXP),diameter of the contraction section of the mixing chamber,and diameter of the diffuser.Nakagawa et al.[12]conducted experimental studies on the flow structure of the ejector,and pointed out that the length of the mixing section affects not only pressure recovery but also entrainment ratios.Dong et al.[13]established a three-dimensional numerical model to investigate the effect of the length of mixing chamber on the performance of steam ejector under different degrees of the Mach number in nozzle exit,the length of constant-area section and the length of diffuser.The results showed that the mixing chamber plays an important role in the performance of the ejector.

The function of the mixing chamber of the ejector is to mix the two fluids of the primary flow and secondary flow and ensure momentum and heat transfer[14].Avila et al.[15]proposed a novel MLPG–finite volume method to obtain accurate pressure and velocity fields of the mixing flow.Zhu et al.[16]used CFD analysis to investigate the influence of the convergence angle of the mixing chamber on the mixing effect of the ejector.Wu et al.[17]studied the effects of the length and convergence angle of the mixing chamber on the performance of the ejector.Fu et al.[18]proposed a method to optimize the diameter of the mixing chamber.Abdel-hamid et al.[19]added a tail section to the mixing chamber of the ejector and studied the influence of the diameter of the tail section on the performance of the ejector.Serra-Pallares et al.[20]developed a method to optimize the conical mixing chamber of the ejector.Chen et al.[21]proposed a method to design a cylindrical mixing chamber on the basis of actual gas characteristics.Ameur et al.[22]carried out an experimental study to analyze the influence of the mixing chamber and diffuser on the performance of the ejector under different working conditions.The function of the diffuser is to convert the kinetic energy of the mixed fluid into pressure energy.Yuan et al.[23] researched the effect of the expansion range of the diffuser on the performance of the ejector.Elbel et al.[24] experimentally tested different diffuser angles and concluded that when the diffuser angle was 5°, the diffuser showed the best performance.However, Banasiak et al.[25]conducted experimental and numerical assessments of the expansion range of the diffuser,and found that 3°was the best expansion angle of the diffuser.Therefore,previous studies have shown that the expansion angle and length of the diffuser have an important influence on the pressure lift of the ejector.The suboptimal expansion angle and length of the diffuser are detrimental to the performance of the ejector.

Although there are many studies on the geometry of the ejector, there are few studies on the radial dimensions of the ejector.The axial dimensions of the ejector, including the position of the nozzle exit,length of the mixing chamber,and length of the diffuser are rarely studied on the basis a sound theoretical model[26].In particular,the length of the mixing chamber,which is important to momentum and heat transfer, should be given more attention.At present, the length of the mixing chamber and that of the diffuser are mainly determined using the empirical formula obtained on the basis of experimental data [27].However, the empirical formula may not be applicable to different working conditions and working media.The flow of a fluid in the mixing chamber shares many similarities to the Fano flow, which describes the adiabatic flow in a constant-section channel and considers the effect of friction.Thus,a theoretical method can be proposed on the basis of the Fano flow theory to determine the axial dimensions of the mixing chamber.

In this paper, we established a model to calculate the length of mixing chamber on the basis of the Fano flow.An improved method that considers fluid friction and cross-sectional flow variation was proposed to determine the length of the diffuser.To verify the model validity,we compared the theoretical results calculated using the model to experimental data reported in literature.The influence of the outlet temperatureTcand outlet pressurepcof the ejector,expansion ratio(the pressure of the primary flow to that of the secondary flowpg/pe),and diameter ratio(the diameter of the throat of the motive nozzle to the diameter of the mixing chamberdg0/dc3)on the length of the mixing chamberLmwas analyzed.Moreover,the influence of the diffuser lengthLdon the semi-cone angle of the diffuserαand diameter ratio (the outlet diameter of diffuser to the diameter of mixing chamberdc/dc3) was discussed.

2 Mathematical Models

2.1 Mathematical Models of the Mixing Chamber

There were seven key assumptions made to derive the ejector model.First,the fluid flow was a one-dimensional steady flow,and the expansion,compression,and mixing processes were adiabatic.Second,the primary flow was in a stagnant state at the inlet of the ejector and a choked state at the throat of the motive nozzle.Third,the secondary flow was in a stagnant state at the inlet of the suction chamber and a choked state at the inlet of the mixing chamber(Section 2,Fig.1).Fourth,the velocity of the diffuser outlet was ignored.Fifth,the mixing of the primary flow and secondary flow began in Section 2,and constant pressure was maintained in the mixing chamber(pg2=pe2).The mixing of the primary flow and secondary flow was completed in section n.Sixth,positive shock waves occurred in Section 3 of the mixing chamber.Seventh,the friction between steam and the tube wall was considered,and the coefficients of friction in the mixing chamber and diffuser remained constant.

Figure 1:A schematic diagram of the ejector structure

On the basis of the isentropic flow and mass conservation between the ejector inlet and motive nozzle outlet(Section 1,Fig.1),we obtained the Mach numberMag1,pressurepg1,temperatureTg1,and mass flow rate ˙mgof the primary flow in Section 1.Moreover, on the basis of the isentropic flow and mass conservation between the motive nozzle outlet and mixing chamber inlet Section 2,we obtained the Mach numberMag2, temperatureTg2, and cross-sectional areaAg2of the primary flow in Section 2.Similarly,the pressurepe2,temperatureTe2,and mass flow rate ˙meof the secondary flow in Section 2 were calculated on the basis of the chock in Section 2.The detailed processes to calculate the parameters of the primary flow and secondary flow were reported in reference[28].

2.2 The Length of the Mixing Chamber(Lm)

2.2.1 The Length Between Section 2 and Section n(Lm1)

Assuming that the mixing of two streams was completed in section n, we divided the length of the mixing chamber into two parts:the length of the mixing section(Lm1)that is located between the Section 2 and section n(Fig.1)and the length of the mixed section(Lm2)that is located between section n and Section 3(Fig.1).On the basis of the assumption about constant-pressure mixing,we established equations to calculate the conservation of momentum and energy along the inlet of the mixing chamber(Section 2)and end position of mixing(section n).In section n,the velocityVn,temperatureTn,and Mach numberManof the mixed fluid are:

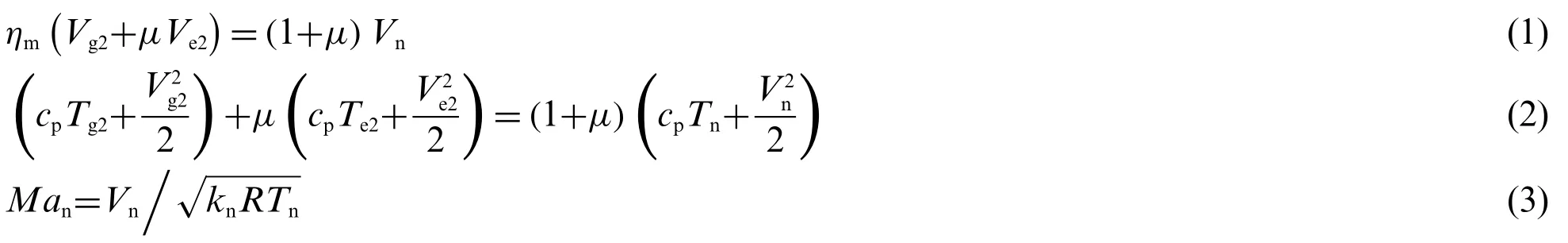
whereηmwas the mixing efficiency,μwas the entrainment ratio,andRwas the gas constant.

In addition,alongLm1,two streams were mixed and the cross-sectional area of the primary flow changed due to the expansion of the primary flow.The mass flow rates of the two streams fluctuated due to the entrainment mechanism.Considering the change in the cross-sectional area of the primary flow,the variations in total temperatureT*and mass flow rate of primary flow ˙mgwere deemed to be linear.Thus,Lm1was calculated on the basis of a geometric relationship:

whereθwas the semi-cone angle of the mixing chamber.

Due to variations in the cross-sectional area and frictional resistance of the fluid, the Mach number of the fluid was expressed by the following[27]:

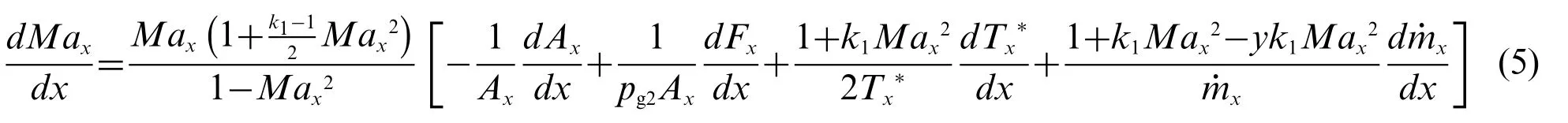
wherexwas the distance to Section 2.The variation in the conical channeldAx/dxwas expressed as:

The changes in the total temperatureand mass flow rateof the primary flow in Section x were calculated according to:

The flow resistance of the primary flow was:

The distribution of the radial velocity of the secondary flow in Section 2 was a nearly exponential distribution,and the detailed calculation was reported in reference[29].

2.2.2 The Length between Section n and Section 3(Lm2)

After section n, the primary flow and secondary flow were completely mixed, and the crosssectional area of the mixed flow remained unchanged.On the basis of the Fano flow model, the viscosity of the mixed fluid and friction between the fluid and wall of the mixing chamber were considered, and the Mach number of the mixed fluid in the outlet of the mixing chamberMac3was calculated according to[30]:

wherefnwas the coefficient of friction that was expressed as[28]:

Adiabatic indexk2was calculated according tok2=(kn+kc3)/2.The temperatureTc3and pressurepc3of the mixed fluid in Section 3 were defined as:

Assuming that a normal shock wave was generated at the exit of the mixing chamber(Section 3),the pressureps,temperatureTs,and Mach numberMasof the mixed fluid after the shock wave were:

wherek3was calculated according tok3=(kc3+ks)/2.Then,on the basis of the isentropic relationship between Section 3 and section c,the pressure and temperature of the fluid in section c were calculated:

whereηdwas the efficiency of the diffuser,andk4was calculated according tok4=(kc3+kc)/2.Thus,Lmwas calculated according to Eq.(19):

Fig.2 shows a flowchart of the calculation process ofLm.On the basis of reference [28], we obtained the parameters of the fluid, such as theManof the fluid in section n.Lm1was calculated using Eq.(4).Then,the Runge–Kutta method was used to solve Eq.(5)and obtainedMax.WhenMaxandManconverge,the corresponding length wasLm1.Otherwise,anotherθwas used to make another calculation untilMaxandManconverge.To obtainLm2, we assumed an initial value ofLm2before calculatingMac3using Eq.(10).Then,Tcwas calculated using Eqs.(12)–(18).WhenTcconverged intoTce,Lm2was obtained.Otherwise,newLm2was re-assigned untilTcandTceconverge.Eventually,Lmwas obtained on the basis of the sum ofLm1andLm2.

Figure 2:A flowchart of the calculation process of Lm

2.3 Mathematical Models of the Diffuser

By assuming that the mixed fluid was stagnant in the ejector outlet, we determined the Mach number of the mixed fluid in the ejector outletMac:

When the semi-cone angle of the diffuser was assumed to beα(Fig.1),the diffuser lengthLdwas expressed as:

Under the action of friction and variation in the cross-sectional area, the Mach number of the fluid in the diffuser was expressed as[27]:

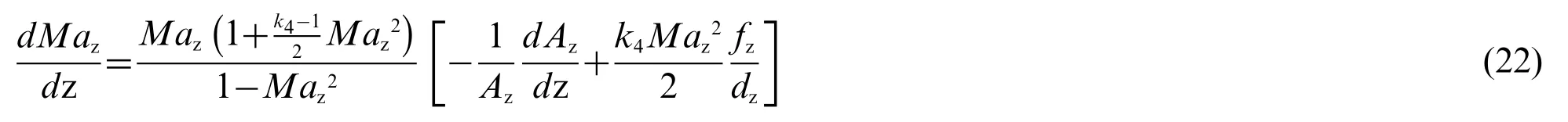
wherezwas the distance to the exit of the mixing chamber(Section 3),and the diameter of sectionzwasdz=dc3+2ztanα.The coefficient of friction of section zfzwas expressed asfz=(fc3+fc)/2,and the initial value of the Mach number wasMac3.

Ldwas calculated by determining the outlet parameters of the mixing chamber and calculatingMacusing Eq.(20).The outlet parameters of the mixing chamber were used as the input parameters of the diffuser.Then,Ldwas calculated using Eq.(21).Moreover, the corresponding Mach number of the fluid in the diffuserMazwas obtained using Eq.(22).WhenMazandMacconverged, the correspondingαandLdwere determined.Otherwise, a newαwas used and the calculation was repeated untilMazandMachad converged beforeLdwas determined.

3 Model Validation

The accuracy of the present model was verified by comparing the theoretical results calculated using the model to the experimental data reported in reference [28].When R141b was used as the working medium, the inlet pressure and temperature of the ejector, diameter of the throat of the motive nozzle,diameter of the outlet of the motive nozzle,and diameter of the mixing chamber were consistent with the experimental values reported in reference[28].Furthermore,the efficiency of the motive nozzleηg,efficiency of the primary flow leaving the nozzleηg1,efficiency of the suction chamberηe,and efficiency of the diffuserηdwere 0.95,0.88,0.85,and 0.80,respectively.The mixing efficiencyηnwas determined according to reference [28].The entrainment ratioμ, outlet temperatureTc, and outlet pressurepcwere calculated and compared to the experimental data reported in reference[28].

Table 1 showsμvalues calculated using the present model and those obtained with experiments.The maximum error was 11.11%,the minimum error was 0.04%,and the average error was 6.76%.

Table 1:Theoretical entrainment ratios calculated using the present model and experimental entrainment ratios reported in reference[28]

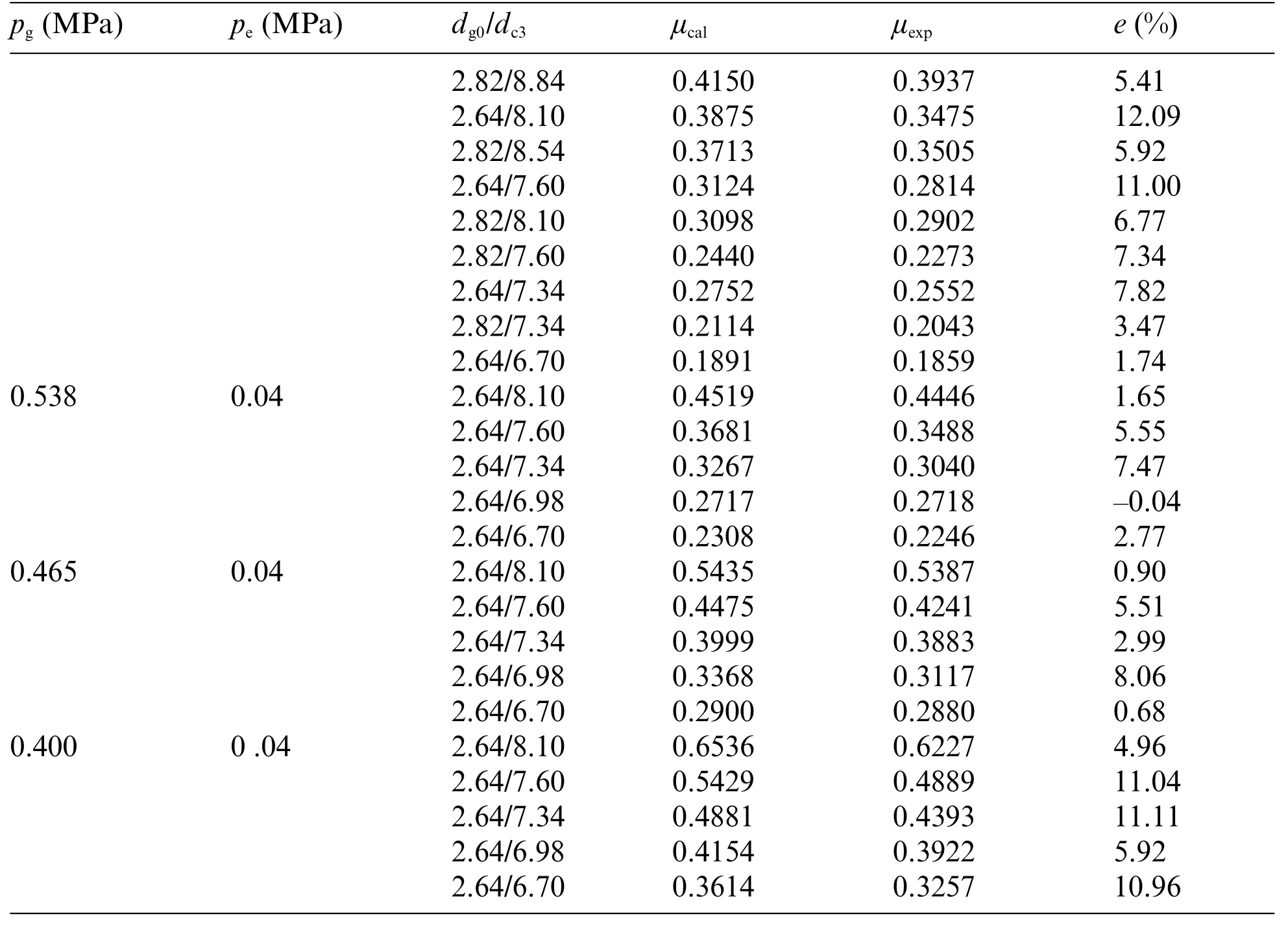
Table 1 (continued)

Fig.3 shows comparisons betweenTcvalues calculated using the present model and those obtained on the basis of experiments.Fig.4 shows comparisons betweenpcvalues calculated using the present model and those obtained on the basis of experiments.As shown in Fig.3,the maximum error and average error of the calculatedTcvalues were 4.49%and 0.79%,respectively.As shown in Fig.4,the maximum error,minimum error,and average error of the calculatedpcvalues were 15.41%,0.05%, and 6.33%, respectively.Due to the position of the nozzle exit, theoretical and experimental heat transfer and friction inevitably differ.

Figure 3:Comparisons between Tc values calculated using the present model and those obtained on the basis of experiments

Figure 4: Comparisons between pc values calculated using the present model and those obtained on the basis of experiments

4 Discussion

On the basis of the structure and working conditions of the ejector reported in reference [28],the length of the mixing chamberLmwas analyzed under different degrees of expansion ratiopg/peand diameter ratiodg0/dc3.Moreover, relationships among diffuser lengthLd,pg/pe, anddc/dc3were discussed.

4.1 The Relationship between Lm and pc and That between Lm and Tc

Fig.5 shows the relationship betweenLmandTcunder different degrees ofpg/peanddg0/dc3.The relationship betweenLmandpcunder different degrees ofpg/peanddg0/dc3is shown in Fig.6.Under different degrees ofpg/peanddg0/dc3, an increase inLmdecreasesTcandpc.Moreover, whenLmandpg/peare constant, an increase indg0/dc3increasesTcandpc.WhenLmanddg0/dc3are constant, an increase inpg/peincreasesTcandpc.Due to the friction between the fluid and tube wall,the longer theLm,the greater the energy loss of the mixed fluid,which decreasesTcandpc.Whendg0/dc3increases,the entrainment ratio and outlet pressure of the motive nozzle increase,which increasesTcandpc.The larger thepg/peis, the greater the pressure recovery, and the greater thepcandTc.Thus,Lmanddc3should be increased to reduceTcandpc.

4.2 Variations in Lm

Fig.7 shows the variations inLm1andLm2with respect to variations indg0/dc3andpg.Figs.7a and 7b show that a decrease indg0/dc3increasesLm1and decreasesLm2.Whendg0/dc3andpeare constant,Lm1increases andLm2decreases with the decrease ofpg.Whenpgis 0.538 or 0.604 MPa,Lm2increases and then decreases.Whenpgis 0.465 or 0.420 MPa,Lm2decreases and then increases.An increase indc3decreases the flow velocity and increasesLm1.Whenpgincreases,the flow rate of the primary flow in Section 2 increases.Whendc3decreases, the intensity of the mixing process increases and Mach number of the fluid in section nManincreases,which decreasesLm1.The regularity ofLm2,which was calculated on the basis of the Fano flow model,is not as obvious as that ofLm1.The main reason is the sensitivity of the friction coefficient model to working conditions.Moreover,whendc3decreases andpgincreases,the flow distance based on the Fano flow increases,which increasesLm2.

Figure 5:Variations in Tc with respect to variations in Lm under different degrees of pg/pe and dg0/dc3

Figure 6:Variations in pc with respect to variations in Lm under different degrees of pg/pe and dg0/dc3

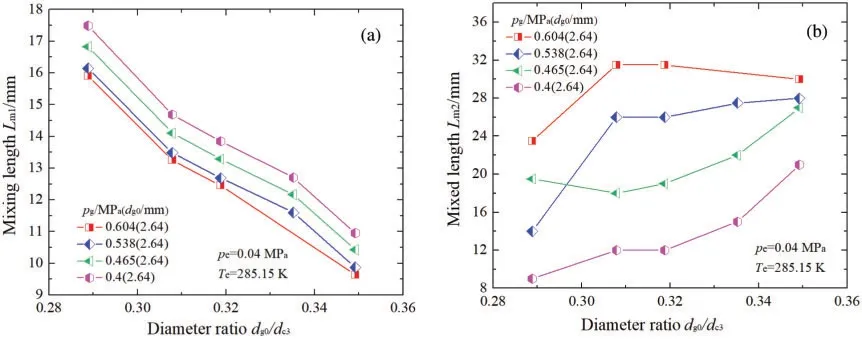
Figure 7:Variations in Lm1 and Lm2 with respect to variations in dg0/d3

4.3 Variations in α and Ld

Fig.8 shows the variations inαwith respect to the variations indc/dc3under different degrees ofpg/peanddg0/dc3.Whenpg/peis constant,αincreases asdc/dc3decreases.Whenpg/peanddc/dc3are constant,αincreases asdg0/dc3increases.Moreover, whendc/dc3anddg0/dc3are constant,αincreases aspg/peincreases.Under a range at whichdc=1.8dc3–2.0dc3,αranges between 6° and 12°.The recommended range ofαwas reported in references [24] and [25], but there are no significant differences between the calculated using the present model and the recommended in literature.The main reason is the diversity of working conditions such as the working medium and structures of the motive nozzle and mixing chamber.

Figure 8:Variations in α with respect to variations in dg0/dc3

Fig.9 shows the variations inLdwith respect to the variations indc/dc3under different degrees ofpg/peanddg0/dc3.As shown in Fig.9,whenpg/peis constant,Ldincreases approximately linearly asdc/dc3increases.Whenpg/peanddc/dc3are constant,Lddecreases asdg0/dc3increases.However, whendg0/dc3anddc/dc3are constant,Ldincreases aspg/pedecreases.Under a range at whichdc=1.8dc3–2.0dc3,Ldranges from 9.7 to 34.2 mm.

Figure 9:Variations in Ld with respect to variations in dc/dc3

4.4 Variations in Tc and pc with Respect to Variations in Ld

Fig.10 shows the relationship betweenLdandTc,and Fig.11 shows the relationship betweenLdandpc.Whendc/dc3is constant, an increase inLdreducesTcandpc.Especially,Tcandpcdecrease significantly whendc3increases from 6.70 to 6.98 mm.Moreover,whenTcorpcis constant,the larger thedc/dc3, the larger theLd.This is reasonable because an increase inLdincreases friction loss and decreasesTcandpc.

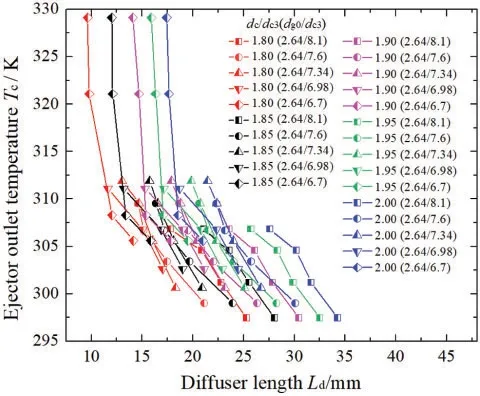
Figure 10:Variations in Tc with respect to variations in Ld

Figure 11:Variations in pc with respect to variations in Ld

4.5 The Distribution of Flow Fields in the Ejector

The two-dimensional CFD model was further developed by using Ansys software to obtain the distribution of flow fields in the ejector.Fig.12 shows the geometric dimensions of the axisymmetric half-space ejector,which were determined on the basis of the experimental data reported in reference[28]except for the length of the mixing chamber.The corresponding grid chart is shown in Fig.13.On the basis of the results of the above analysis,we choseLdto be 32.29 mm andαto be 10°.Details on the operating conditions of the ejector are listed in Table 2.

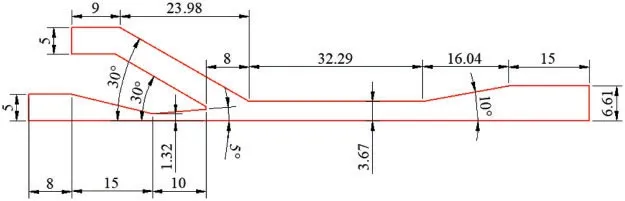
Figure 12:Geometric dimensions of the axisymmetric half-space ejector(length unit:mm)

Figure 13:The grid chart of the ejector

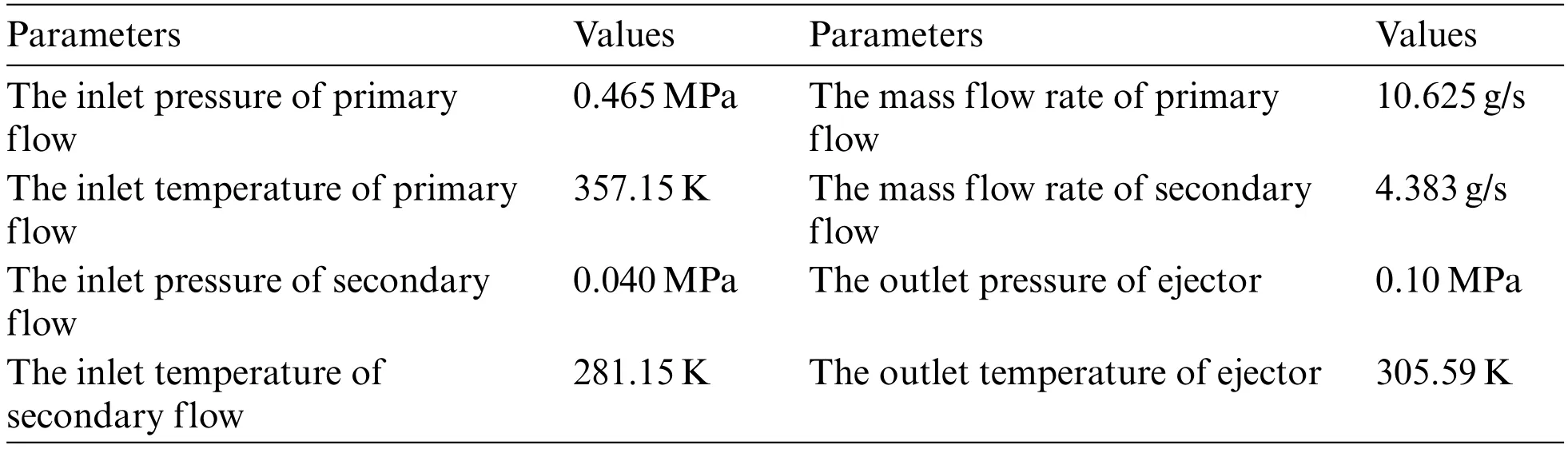
Table 2: Operating conditions of the ejector

Fig.14 shows the distribution of flow fields in the ejector,including the distribution of pressure,temperature, velocity, Mach number, and streamline of the fluid in the ejector.Fig.14a shows that pressure reduces and then increases along the axis of the ejector, and there is a shock wave in the mixing chamber.As shown in Fig.14b, due to entrainment in the suction chamber, a low-pressure region is produced and temperature decreases.In addition,the distribution of the Mach number,which is shown in Fig.14c,and that of velocity,which is shown in Fig.14d,indicates that the velocity of the fluid reaches supersonic speed in the nozzle throat, and theMaof the fluid is close to 1.0.Then,the fluid with supersonic speed leaves the motive nozzle and flows to the location of the shock wave.Fig.14e shows the fluid streamline in the ejector.The secondary flow enters the suction chamber,and the two streams begin to mix before flowing out of the ejector.

Figure 14:Flow field distributions in the ejector

5 Conclusions

In this paper,an improved model to calculate the mixing chamber length was established on the basis of the Fano flow model,and a method was proposed to optimize the diffuser structure,which considered the frictional resistance and changes in cross-sectional area.To ensure the validity of the model,we compared the theoretical results calculated using the model to experimental data reported in literature.The average error of the calculated entrainment ratioμwas 6.76%,the average error of the calculated outlet temperature of ejectorTcwas 0.79%,and the average error of the calculatedpcwas 6.33%.

Variations in mixing chamber lengthLmand diffuser lengthLdwith respect to variations inTcandpcwere investigated.Variations in mixing section lengthLm1and mixed section lengthLm2with respect to variations in diameter ratiodg0/dc3were discussed.Relationships amongLd,expansion ratiopg/pe,and diameter ratiodc/dc3were analyzed.The distribution of flow fields in the ejector was obtained.

An increase inLm1decreasedTcandpc.Decreases inpg/peanddc3reducedTcandpc.Furthermore,a decrease in primary flow pressurepgand an increase in mixing chamber diameterdc3increasedLm1.Lm2andLm1showed an opposite trend.

A decrease inpg/peand an increase indc/dc3reduced the semi-cone angle of the diffuserα.Decreases inTcandpcincreasedLd.Moreover,whenTcorpcwas constant,the larger thedc/dc3,the larger theLd.

In the future,to perform more complicated and flexible computer-aided design(CAD),we will employ Non-Uniform Rational B-Splines(NURBS)to represent the geometry of the ejector.Then,isogeometric analysis [31] will be performed on the basis of the Fano flow model to connect CAD and numerical analysis.By using the control points of NURBS as design variables, we will adopt a gradient-based shape optimization algorithm to automatically search a large design space for the optimal geometry of the ejector.Furthermore,we will investigate the application of the isogeometric boundary element method,which has boundary representation properties,to reduce the dimension of the problem and facilitate the variation in geometry,thus,alleviate the mesh burden associated with iterative shape optimization procedures[32,33].

Funding Statement:This work was supported by the National Natural Science Foundation of China(Grant No.51806132), Central Guided Local Science and Technology Development Foundation(Grant No.YDZX20201400001939), and Scientific and Technological Innovation of Colleges and Universities of Shanxi Province(Grant No.201802011).

Conflicts of Interest:The authors declare that they have no conflicts of interest to report regarding the present study.