一种计及电动机负荷模型的配电系统状态估计方法

曹立霞，卞孟哲，陈立征，郑学汉，王 艳

(1.山东建筑大学信息与电气工程学院，山东 济南 250101；2.山东省智能建筑技术重点实验室；3.国家电网山东省电力公司经济技术研究院)

0 引言

近年来，随着大量新型能源在配电网中的接入，以及用户用电需求的提高，电力系统的稳定性需得到进一步的提升。为了应对复杂条件下配电网的正常运行，以及满足用户用电质量和用电可靠性的需求，配电管理系统应全面准确地获取配电网运行状态。

在配电网状态估计的研究中，有研究提出负荷建模的精确性对于状态估计精度的影响。文献[4]提出了在脉冲神经网络的基础上，对伪量测进行建模的方法，但是该方法的节点负荷模型研究都是基于恒功率负荷模型，并未考虑电压特性对负荷的影响。文献[5]在传统状态估计算法的基础上进一步结合了更复杂的静态负荷模型。由于电动机在负荷中所占比重日益升高，且传统的静态负荷模型不能准确地反映电动机负荷特性，因此，在配电网系统分析中有必要考虑计及电动机负荷特性的负荷模型。

本文在配电网状态估计的基础上，结合实际配电网负荷情况，提出了一种计及电动机负荷模型的配电网状态估计方法。该方法通过感应电动机并联ZIP 的负荷模型来替代传统的恒功率模型或静态负荷模型，构建负荷节点的零注入量测和转矩量测函数，考虑了电压特性对于节点负荷的影响。最后，我们利用IEEE33 节点的配电系统进行算例仿真，结果表明，该算法能够有效地提高配电网状态估计准确度。

1 配电系统状态估计的一般模型

加权最小二乘法(WLS)是一种广泛应用于配电系统状态估计的算法，通过量测数据和网络拓扑信息求取最优状态变量，以量测误差加权平方和最小为目标函数。目标函数如式⑴：

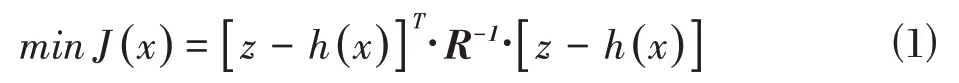
量测量与系统状态变量的非线性关系如式⑵。

本文选取以节点电压有效值和相角为状态变量的节点电压法，原因如下：

⑴以电压和相角为状态变量便于利用各种量测量，构造相应的量测函数，达到量测值的最大化利用，从而状态估计精确性较高；

⑵由于负荷模型与节点的电压密切相关，因此节点电压法便于描述相关负荷模型，有利于构造负荷节点的量测函数和获取雅可比矩阵。

2 负荷模型

由于配电网中负荷类型较为复杂，不仅包含了大量的电动机负荷，同时还包括了各种静态负荷成分。在传统状态估计中，节点负荷模型通常采用静态负荷模型，静态负荷模型虽能反映负荷的电压特性，但该模型并不能描述配电网中大量的感应电动机负荷，因此，为了更为准确地描述配电网负荷特性，本文将ZIP 静态负荷模型和感应电动机模型相结合，采用如图1所示的计及电动机特性的负荷模型。

图1 感应电动机并联ZIP负荷模型

图1 中，表示配电网的节点电压；为感应电动机负荷模型内电势节点；分别为恒阻抗、恒电流和恒功率的静态负荷模型；R、X、X、、、X分别为电动机负荷模型中定子电阻、定子电抗、转子电抗、转子电阻、电动机转差率和励磁电抗。

电动机并联ZIP负荷模型包含以下两部分：

配电网中，节点的ZIP 静态负荷模型采用如下的多项式形式如下：

其中，分别为负荷的额定有功功率、无功功率；a（a）、b（b）、c（c）分别为有功（无功）恒定阻抗、恒定电流、恒定功率负荷的系数，且有：

感应电动机的暂态微分方程如下：

其中，为感应电动机内电势，T为转子绕组时间常数，为定子侧电源频率，为角速度，下标、分别为转子侧量、定子侧量，T、T分别为感应电动机的电磁转矩、机械转矩，为惯性时间常数。

电动机负荷模型内电势节点的有功功率和无功功率表达式如下：

电动机的电磁转矩T、机械转矩T的表达式如下：

其中，为感应电动机初始负荷率，为机械转矩系数。

由以上分析得出，配电网节点的感应电动机模型为：

图2 感应电动机稳态等值电路

3 计及电动机负荷模型的配电系统状态估计

对于个节点（其中负荷节点的数量为个）的配电系统，在系统拓扑结构的基础上，通过在负荷节点增加电动机负荷模型内电势节点，如图1所示，从而将电动机负荷模型与配电网状态估计方法相结合。配电网由原来的个节点变为+个节点，新增的状态变量分别为电动机内电动势有效值和相角、电动机转差率，电动机定子电阻和定子电抗所在的支路为配电网新增支路，此时，将电动机内电动势有效值改用符号表示。

在负荷节点增加了电动机负荷模型内电势节点之后，对于配电网原有的个负荷节点，建立如下的节点零注入功率虚拟量测方程：

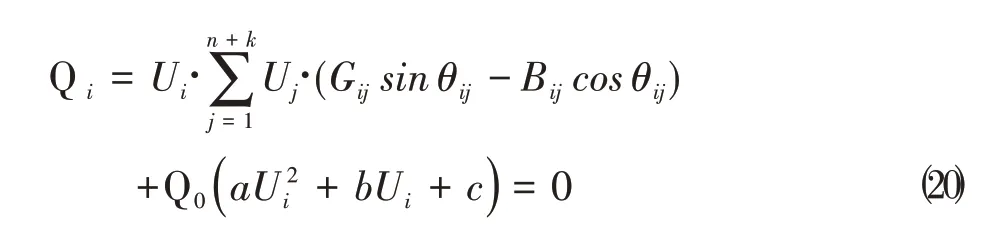
其中，P 、Q 为配电网节点注入有功功率、无功功率，节点为负荷节点，=12…+，第+1+2…+为个新增的电动机负荷模型内电势节点；U、U分别为节点、的电压有效值；G、B分别为节点、之间的电导和电纳；θ=θ-θ为节点、之间的电压相角差。

对于配电网原有的-个非负荷节点，节点注入功率量测方程如下：

对于配电网新增的个电动机负荷模型内电势节点，构造功率零注入虚拟量测方程如下：

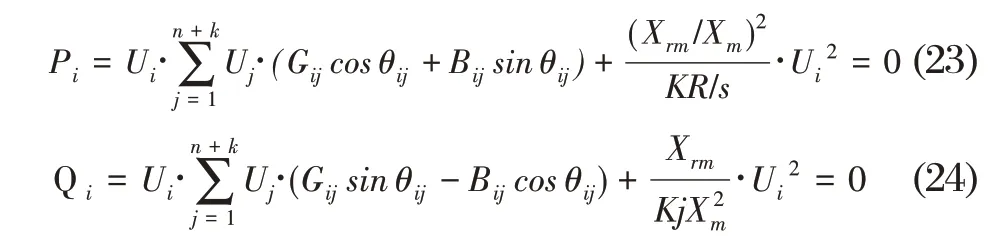
其中，=+1+2…+;为容量折算比。

构造电动机转矩零注入虚拟量测方程如下：

由此可见，当计及感应电动机并联ZIP 的负荷模型后，配电系统量测量在原来量测的基础上增加了负荷节点零注入功率虚拟量测、电动机节点的零注入功率虚拟量测和电动机节点的转矩零注入虚拟量测；相应地，量测量对于状态变量的导数矩阵，即雅可比矩阵也随之变化，最大变化在于需要计算原有的量测量需对感应电动机转差率的一阶偏导，对新增的感应电动机节点电压的有效值和相角的一阶偏导。

4 算例仿真与分析

将本文提出的计及电动机负荷模型的状态估计方法应用于IEEE33节点的配电系统进行算例仿真。本文采用MATLAB2016 编程，根据文献[6]中所提到的当前实际应用中典型的配电网负荷模型参数，以及静态负荷模型和电动机负荷模型的占比。假设4、14、25、30 节点采用感应电动机并联ZIP 的负荷模型，感应电动机参数参考中国电科院的电动机模型，如表1所示。

表1 电动机模型参数表

本文采用平均绝对误差，作为衡量状态估计值与真实值之间误差情况的指标。平均绝对误差定义为：

通过在潮流计算结果上叠加正态分布的随机误差，产生100 组量测量。分别采用考虑ZIP 负荷模型的传统状态估计方法和本文提出的方法进行状态估计，图3、图4 分别展示了传统状态估计方法和计及电动机负荷模型状态估计方法在节点电压幅值和相角上的平均绝对误差值。

图3 节点电压有效值平均绝对误差

图4 节点电压相角平均绝对误差

从图3、图4 中可以看出，计及电动机并联ZIP 负荷模型后状态估计变量的误差变小，状态估计结果更接近于真值。因此，本文提出的方法能够提高配电网状态估计的准确度。

5 结束语

本文在静态负荷模型的基础上，结合实际配电网负荷情况，考虑了配电网中占比较大的电动机负荷。通过并联两种负荷模型，构造负荷节点新的零注入功率量测函数和雅可比矩阵。仿真结果证实了该方法不仅能够提高状态估计的准确度，而且具有较好的实用性。

但随着分布式能源的快速发展，负荷的复杂性、波动性、主动负荷的比例不断提高，需进一步完善配电网的负荷模型，更深入地研究负荷模型对配电网状态估计的影响。