基于阻尼最小范数法的四轴转台逆运动学算法分析

林笑亦,刘 军,苏 浩,钟正虎

（北京航天控制仪器研究所,北京 100039）

0 引言

在半实物仿真系统中,三轴仿真转台是最常用的硬件设备［1］,可以模拟飞行器在空间中滚转、俯仰和偏航三个姿态的变化,从而复现飞行器运动时的各种姿态运动及动力学特性,最终实现飞行器整体设计的性能优化。对于三轴仿真转台,每一个轴对应一个姿态角,物理含义明确,因此应用非常便利。但是,如果三轴转台在工作的过程中出现两轴重合的情况,就会由三个自由度退化为两个自由度,从而出现运动学奇异,无法模拟空间三个自由度的姿态运动。除此之外,当三轴仿真转台在邻近奇异位置运动时,其运动学传递特性会急剧变差,极大地增加了转台的研制难度。为了克服上述的运动学奇异性问题,四轴全姿态仿真转台的发展有着重要的意义［2］。

四轴转台是在三轴转台的基础上增加一个冗余轴,利用冗余自由度机构的特点［3-6］来规避三轴转台面临的运动学奇异性问题,从而实现飞行器空间运动的全姿态全弹道仿真,对于大角度机动飞行器的研制具有极其重要的意义［7］。对于四轴转台,在初始状态下有两个运动轴重合,各轴的转角与飞行器的姿态角没有一一映射关系,因此对于某种确定的飞行状态,四轴转台有无数种框架角与之对应。同时,由于四轴转台各轴转角与姿态角的映射为非线性关系,进一步增加了框架角解算的难度。因此,如何求得最优框架角成为四轴转台设计和研究的技术难点。目前,针对四轴转台控制策略的研究还相对较少。2010年,瑞士ACUTRONIC公司的Carter等［8］通过加权最小二乘法建立了四轴转台的框架角约束优化条件。当转台在远离奇异位置的区域时,其按照三轴转台运行;当转台临近奇异位置时,通过自适应调整基框架权值,使转台按照四轴转台运动,从而远离奇异位置。同年,王晓晨等［9］通过梯度投影法求得了带有指标优化的框架角速度最优解,并应用动态控制实时计算了四轴转台最优框架角。2015年,基于约束优化理论,徐勤贝［10］通过Lagrange乘子法计算得到了四轴转台的最优框架角。2017年,赵军虎等［11］提出了一种四轴平台随动回路的方法,即当外框架角等于±90°时,可以调整随动框架旋转90°以使得平台规避不稳定位置。

基于以上研究,本文提出了一种基于阻尼加权最小范数法的四轴转台框架角解算算法,在约束最小角速度的同时引入了权值分配和变阻尼因子,从而增强了四轴转台规避奇异的能力以及运动学逆解的奇异鲁棒性,达到了实现全姿态仿真的目的。本文首先基于四元数法对四轴转台进行了正运动学分析,给出了四轴转台的运动学模型。其次,通过阻尼加权最小范数法构建了四轴转台的最优化条件并引入阻尼因子,得到了四轴框架角速度的奇异鲁棒性解,通过闭环逆运动学算法得到了四个框架角,并进一步通过二次优化提高了框架角解算的精度,确保了飞行器姿态的准确性。最后,通过仿真对算法进行了验证。

1 四轴转台正运动学分析

1.1 飞行器姿态分析

飞行器在空间中的姿态可以通过地面坐标系与飞行器坐标系之间的转换矩阵来表示。现定义飞行器坐标系是按照Y-Z-X的顺序旋转得到,其旋转过程如图1所示。首先,飞行器绕惯性坐标系Oy轴旋转ψ角,得到中间坐标系O-x′yz′;再绕中间坐标系的Oz′轴旋转θ角,得到中间坐标系O-Xy′z′;最后绕OX轴旋转γ角,得到飞行器坐标系O-XYZ。在此定义下,三次旋转的单位四元数为

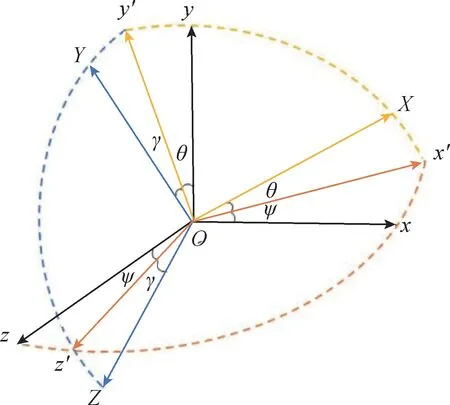
图1 姿态角旋转示意图Fig.1 Schematic diagram of attitude angle rotation

通过飞行器的单位四元数,可以进一步由式（1）计算得到其四元数矩阵

1.2 四轴转台姿态分析

四轴转台是在三轴转台的基础上增加一个与中框架相同方向的基框轴,属于冗余自由度机构。在转台工作过程中,四轴转台利用冗余轴系的运动来避免运动奇异,从而保障转台能够模拟飞行器在空间偏航、俯仰、滚转三个方向上的全姿态运动。四轴转台分为立式和卧式两种,本文研究的是卧式四轴转台,其结构原理图如图2所示。由图2可知,卧式四轴转台是在立式三轴转台的基础上增加一个基框架,其四个框架角由外到内依次为基框、外框、中框和内框,旋转角度分别为δ1、δ2、δ3和δ4,如图3所示。

图2 四轴转台结构原理图Fig.2 Structure schematic diagram of four-axis turntable

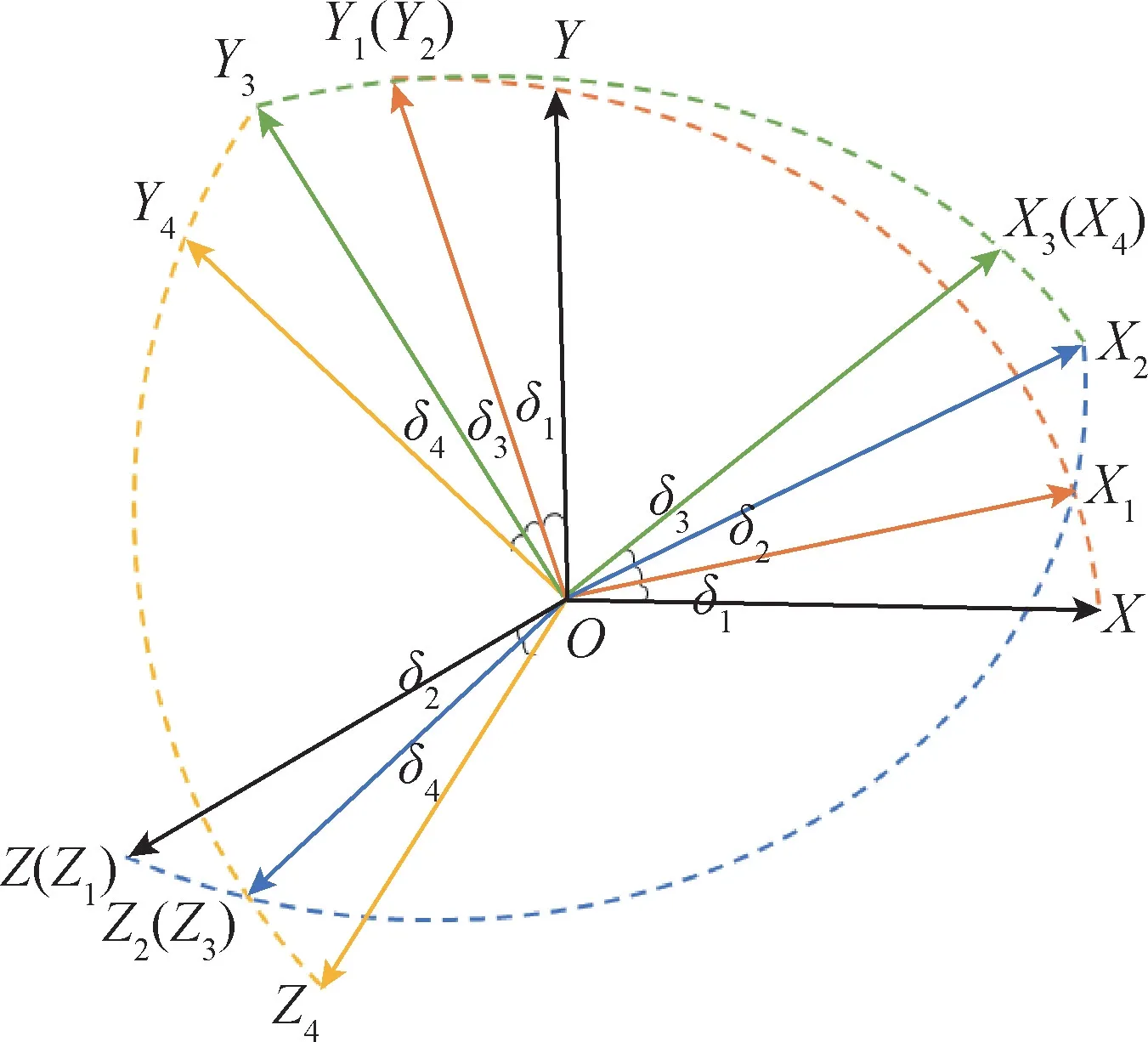
图3 框架角旋转示意图Fig.3 Schematic diagram of frame angle rotation

对于卧式四轴转台,四个框架的单位四元数为

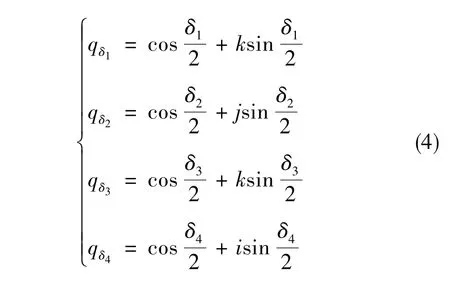
通过各个框架的单位四元数,可以进一步由式（4）计算得到转台上负载的姿态四元数矩阵

式（5）中,q10、q11、q12、q13满足

由于式（2）和式（5）转动等效,可得

由式（7）可知,四个框架角δ1、δ2、δ3、δ4和三个姿态角ψ、θ、γ之间并不是一一对应的关系,在给定三个姿态角的情况下有无数组框架角与之对应。接下来,将通过阻尼加权最小范数法和二次优化得到最优解。

2 四轴转台逆运动学分析

2.1 阻尼加权最小范数法

根据式（7）,将等式对时间求导可以得到

式（9）中,J=Jx+Jδ。

为了计算四轴转台的最优框架角速度,基于加权最小范数法［13-14］构建了式（8）的约束优化条件

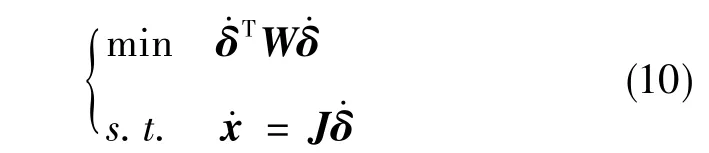
式（10）中,W为加权矩阵,定义如下

式（11）中,w1、w2、w3和w4分别为基框架、外框架、中框架和内框架的权重因子,具体定义后文会详述（2.3节）。

对于式（10）所示的约束优化条件,基于加权最小范数法重新定义加权矩阵和加权框架角速度

因此,对应的式（9）可以表示为

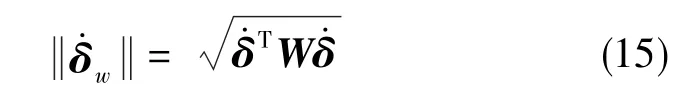
其对应的解为文献［15］中提出的针对冗余自由度机构的加权最小范数解

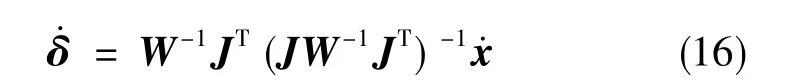
这里的通解与传统最小范数法的通解不同,主要是针对多解问题的最小范数解。

对式（16）中矩阵JW-1JT进行奇异值分解,可以求得框架角速度的范数为

式（17）中,［a1a2a3a4］T=UT,U由J=UΣVT分解求得,σi为矩阵JW-1JT的奇异值。由式（17）可知,矩阵奇异值越小,框架角速度范数越大,而当奇异值接近于零时,框架角速度范数为无穷大,影响四轴转台的稳定性。因此,本文中进一步引入了阻尼因子λ,得到了加权最小范数法的奇异鲁棒性解

在引入阻尼因子后,可以得到框架角速度的范数解为

由式（19）可知,在引入阻尼因子后,可以有效地避免奇异值过小时框架角速度过大的情况。阻尼因子的设置采用Chiaverini［16］提出的连续可调的阻尼因子设置方法,如式（20）所示。若所求得的σmin小于所设定的临界值,引入阻尼因子可以提升逆解的鲁棒性。

式（20）中,σmin为Jacobi矩阵奇异值的最小数,σ0为最小奇异值临界值,λmax为最大阻尼因子。对于最大阻尼因子λmax以及最小奇异值临界值σ0的选取原则,如果取值过大,虽然可以有效地克服奇异,但是却引入了较大的跟踪误差;相反,如果取值过小,奇异则得不到有效地解决,系统运动平滑性不好。因此,在算法应用的过程中通过反复调整得到两者最优值,从而使框架角能平滑过渡,不会出现太大的瞬时框架角速度。

2.2 基于闭环逆运动学的奇异鲁棒性逆解解算

由于最小范数法属于开环算法,每一次计算的过程中都会产生误差,误差的不断累积会导致求解精度过低。因此,本文进一步引入闭环求解,通过迭代的方式使结果达到求解精度。

式（16）经过离散后,得到

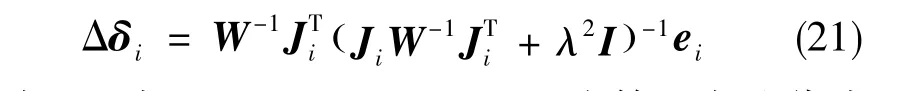
式（21）中,Δδi=δi+1-δi,δi为第i次迭代中当前时刻的框架角位置,δi+1为下一次迭代中的框架角位置,ei=x（k+1）-x。其中,x（k+1）为下一时刻的期望姿态角位置,x为当前时刻的姿态角位置。

为了充分平衡计算时间和计算精度,在算法中的计算误差设置为1×10-3°。为了进一步提升解算精度,本文在每次迭代完成后引入了二次优化。由于每次迭代都以前一时刻的框架角为初始值,因此二次优化还可以提升初始值的准确性,从而提升每次迭代收敛的快速性。

式（22）中,p10、p11、p12、p13满足

进而可以求得二次优化后除基框架角外的其他框架角

综上所述,基于阻尼最小范数法的闭环逆运动学原理框图如图4所示。

图4 基于闭环阻尼最小范数法的运动学逆解框图Fig.4 Block diagram of inverse kinematics solution based on closed-loop damping least-norm method

具体的迭代步骤如下:

1）初始化各个参数,首先初始化框架角δ1（0）、δ2（0）、δ3（0）、δ4（0）以及参数λmax、σ0、ε;

2）计算下一时刻目标姿态角位置x（k+1）和当前时刻姿态角位置x的差值ei;

3）计算Jacobi矩阵Jx和Jδ,同时计算矩阵J=Jδ;

4）计算矩阵J的奇异值最小值σmin,比较σmin和最小奇异值临界值σ0,从而确定阻尼因子的大小;

5）根据Δδi=W-1（JiW-1+λ2I）-1ei计算每一个迭代步中的框架角增量Δδi,令δi+1=δi+Δδi得到下一个迭代步中的框架角;

6）通过运动学正解计算当前时刻的姿态角位置x;

7）根据期望姿态角位置计算误差ei,判断误差ei是否达到求解精度,若ei＞ε,则返回步骤3继续,若ei≤ε,得到满足条件的框架角δ^=δi;

8）应用二次计算模块对δ^进行优化,得到下一时刻的框架角δ（k+1）,返回步骤2进行下一次计算,直至完成计算周期T,迭代结束。

2.3 权重因子优化设计

根据四轴转台的框架结构,由文献［7］可知,当四轴转台的两两轴重合,即δ2=0°且δ3=±90°或δ2=-180°且δ3=±90°时,会产生四轴转台自身运动学奇异,由此引入优化函数H1和H2

定义外框架权重

式（27）中,参数A1、A2、B1、B2根据实际情况确定。

外框架的权重因子w2在特定条件下的变化曲线如图5所示。外框架的权重因子由δ2、δ3确定以规避四轴转台自身的奇异性,当δ2、δ3同时满足奇异条件时,外框架的权重因子w2增大,从而达到规避四轴转台自身奇异位置的目的。

图5 外框架权重因子变化曲线Fig.5 Change curve of outer frame weight factor

由式（16）可知,对于任意的三个目标姿态角都可以由四个框架角表示。在解算中框架角度时,为了避免反三角函数的多解问题,引入了框架角优化指标函数

式（28）中,δ3min≤δ3≤δ3max。

通过优化指标函数,对中框架的权重因子w3进行定义［17］

中框架的权重因子w3的变化曲线如图6所示。可以看出,当中框架接近±90°时,中框架权重因子w3随之增大,趋近于无穷,通过优化权重因子将中框架角约束到了（-90°,90°）的范围内。

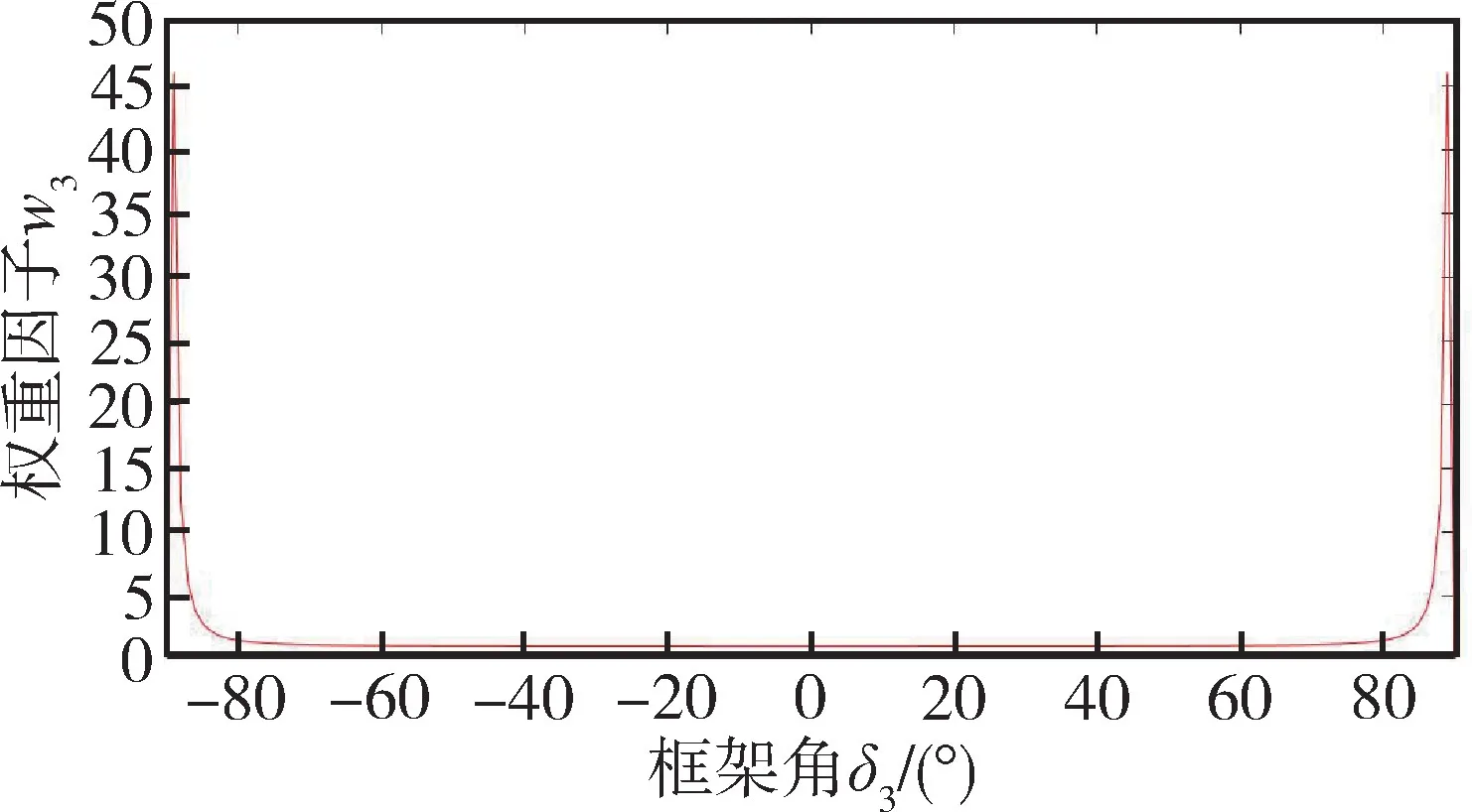
图6 中框架权重因子变化曲线Fig.6 Change curve of middle frame weight factor

根据式（28）,定义基框架权重为

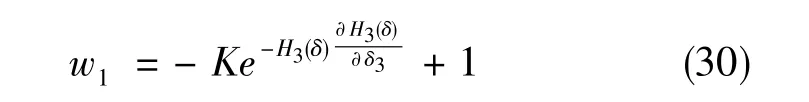
式（30）中,参数K根据实际情况确定。

基框架的权重因子w1随中框架角的变化曲线如图7所示。四轴转台在运动的过程中,当中框架趋于奇异位置时,需要基框架权重值减小,运动速度增大,从而避免奇异;当中框架与奇异位置较远时,则需要增大权重值,减小运动速度,以达到降低电机负荷、提升转台动态性能的目的。

图7 基框架权重因子变化曲线Fig.7 Change curve of base frame weight factor

在四轴转台四个框架中,内框架的动态性能最好,为了保证内框架在转动范围内保持高速运动,设置内框架的权重因子w4=1。

3 仿真分析与实验验证

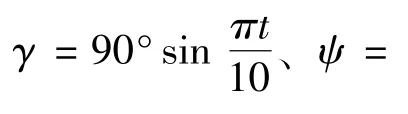
由Matlab计算得到目标姿态角输入下的框架角如图8所示。

由图8可知,飞行器的轨迹中存在俯仰角和偏航角都≥90°的情况,接下来分别用立式三轴转台和卧式三轴转台模拟弹道曲线。

图8 目标姿态角曲线Fig.8 Curves of target attitude angle

根据旋转顺序,可得弹体的角速度

对立式三轴转台,其外框为偏航ψl,中框为俯仰θl,内框为滚转γl。旋转顺序为先偏航、再俯仰、最后滚转,姿态微分方程为

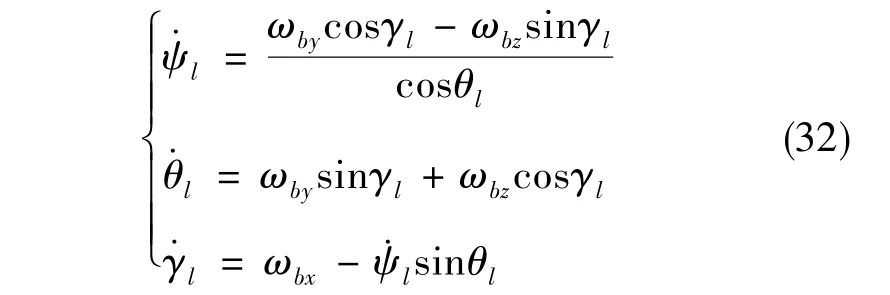
对卧式三轴转台,其外框为俯仰θw,中框为偏航ψw,内框为滚转γw。旋转顺序为先俯仰、再偏航、最后滚转,姿态微分方程为

由式（31）可知,在θl=±90°时,cosθl=0,此时外框和内框重合,导致立式三轴转台丢失一个自由度,产生奇异性,无法模拟负载三个自由度的姿态运动。同理,由式（32）可知,在ψw=±90°时,cosψw=0,此时外框和内框重合,导致卧式三轴转台丢失一个自由度,产生奇异性,无法模拟负载三个自由度的姿态运动。

三轴转台的角速度曲线如图9所示。

由图9可知,无论是立式三轴转台还是卧式三轴转台,在模拟图8给定的弹道曲线的过程中会出现奇异,角速度发生突变从而导致角加速度过大,超过了转台的驱动能力,导致仿真断开。

图9 三轴转台框架角速度曲线Fig.9 Frame angular velocity curves of three-axis turntable

利用本文的运动学反解算法可以得到四轴转台的四个框架角位置变化曲线,如图10所示。其角速度和角加速度曲线如图11、图12所示。

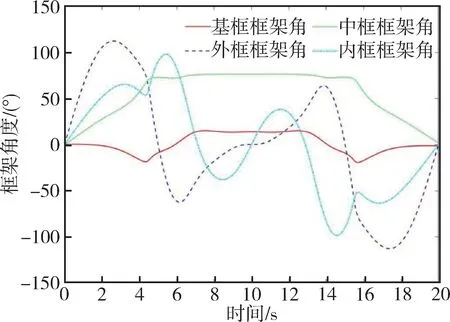
图10 四轴转台框架角位置变化曲线Fig.10 Frame angle position change curves of four-axis turntable

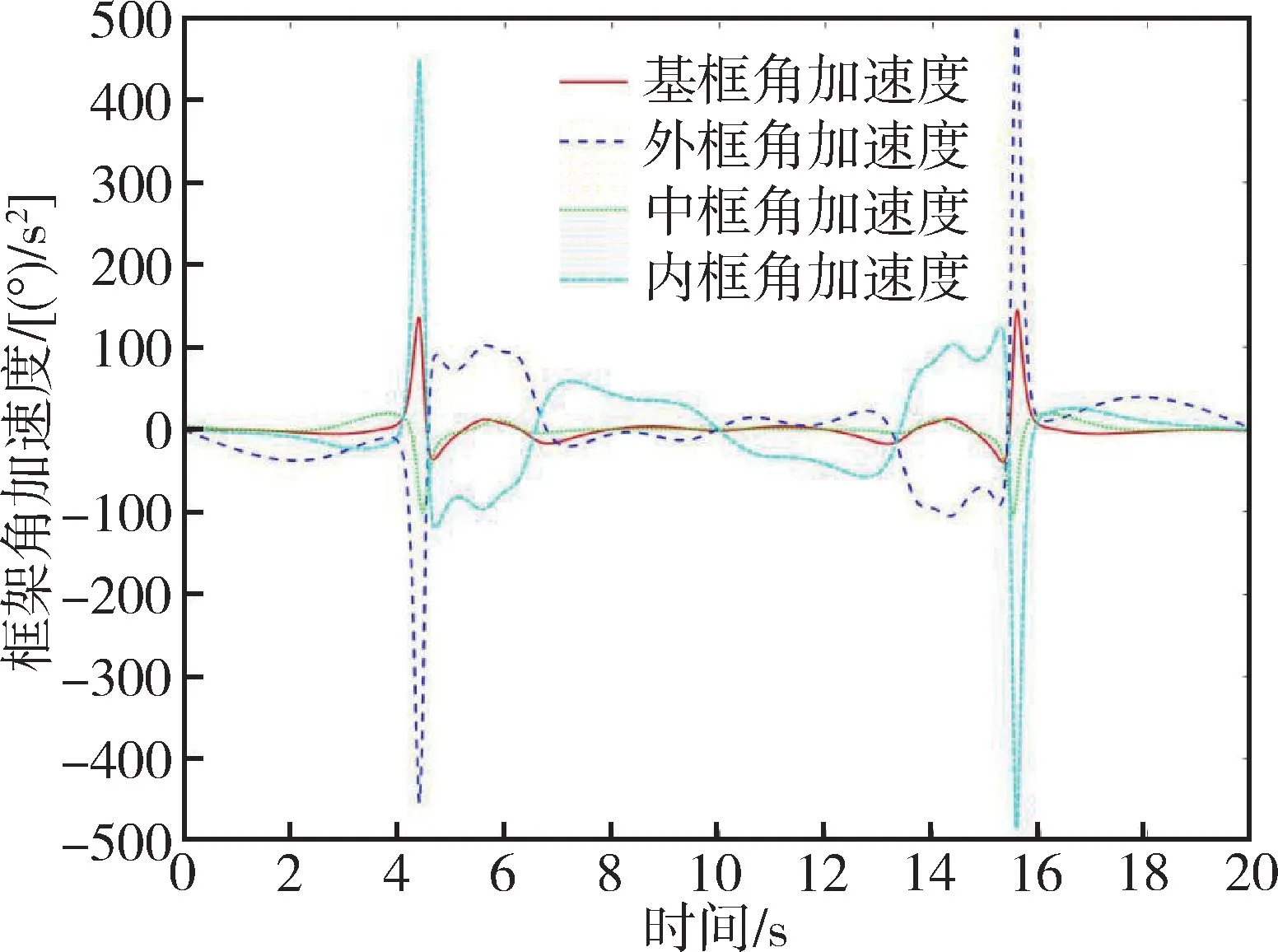
图12 四轴转台框架角加速度曲线Fig.12 Frame angular acceleration curves of four-axis turntable

由图10～图12可知,四个框架角变化平滑,角速度和角加速度都在转台运行范围内,即使在飞行器俯仰角大于90°时也不会出现突变,充分说明了所提出算法的合理性。

为了验证算法的精度,进一步由框架角正运动学计算得到了飞行的姿态角,并分析了输入与输出姿态轨迹之间的误差,如图13所示。

由图13可知,理论计算上,滚转角误差绝对值的最大值为1.1×10-9°,偏航角误差绝对值的最大值为4.9×10-9°,俯仰角误差绝对值的最大值为7.1×10-11°,充分说明了所提出方法的准确性。

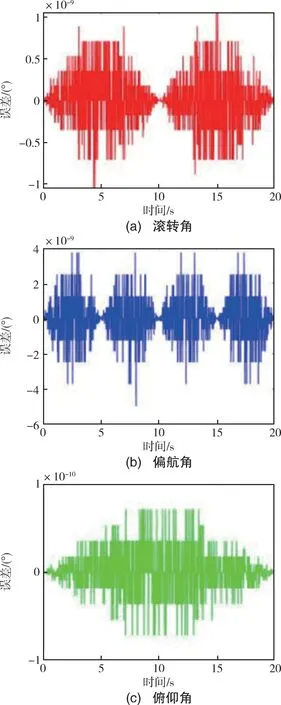
图13 四轴转台的解算误差曲线Fig.13 Calculation error curves of four-axis turntable

最后,通过本单位研制的四轴转台对四轴转台自身的四个框架进行验证,四轴转台实物如图14所示。

图14 四轴转台实物图Fig.14 Physical drawing of four-axis turntable

输入四轴转台的框架运动轨迹,并进一步通过运动学正解运算,得到姿态角的跟踪曲线如图15所示。

由图15可知,姿态角的指令曲线和实际运行曲线（反馈曲线）之间存在一定的偏差,这跟转台控制器设计、机械结构摩擦以及测角元件精度等有关。进一步输出姿态角的幅值跟踪误差,如图16所示。

图15 四轴转台目标姿态角跟踪曲线Fig.15 Target attitude angle tracking curves of four-axis turntable

图16 四轴转台目标姿态角幅值跟踪误差Fig.16 Target attitude angle amplitude tracking error curves of four-axis turntable

由图16可知,滚转角误差绝对值的最大值为2.2×10-3°,偏航角误差绝对值的最大值为2.2×10-3°,俯仰角误差绝对值的最大值为1.9×10-3°,满足转台的技术指标。

综上所述,通过Matlab仿真验证和实验可知,本文所提出的方法能够高精度地解决四轴转台运动学逆解中的多解问题,而且可以确保四个框架角变化平稳,不会出现突变,在误差允许范围内,满足飞行器全姿态仿真的要求［18］。

4 结论

本文基于阻尼加权最小范数法提出了四轴转台的闭环逆运动学求解方法,可以实现四轴转台框架角的高精度解算。在所提出的方法中,结合转台实际工况引入了权重因子和阻尼因子,避免了Jacobi矩阵接近奇异时对算法的影响,充分确保了运算过程的稳定性。由闭环逆运动学计算得到阻尼最小范数法的奇异鲁棒性逆解后,进一步引入了二次优化,不仅降低了运算时间,而且确保了算法的准确性。最后,通过Matlab仿真验证和实验验证了算法的正确性。由仿真结果可知,本文所提出的方法可以平滑地将姿态角高精度地转化为框架角,确保了四轴转台工作过程中的连续性,为大机动飞行器的全姿态仿真奠定了基础。