椭圆曲线y2=3qx(x2-2)的整数点
2022-07-28杜先存刘勇浩余昆艳
杜先存,刘勇浩,余昆艳
椭圆曲线y2=3qx(x2-2)的整数点
杜先存,刘勇浩,余昆艳
(红河学院 教师教育学院,云南 蒙自 661199)

椭圆曲线;正整数点;同余;Legendre符号
1 引言
椭圆曲线的整数点是数论中很重要的问题,关于椭圆曲线


为奇素数时的情况进行研究。
2 引理

至多有2组正整数解。
3 相关定理
定理 若
为互异的奇素数,则椭圆曲线

至多有2组正整数点。
4 定理证明

下面将分别讨论四种情形下(3)的正整数点的情况。

因为Legendre符号值
则(4)式不成立。因此,情形I不成立,即椭圆曲线(2)无正整数点。

因为Legendre符号值
则(4)式不成立。因此,情形II不成立,即椭圆曲线(2)无正整数点。




综上有椭圆曲线(2)至多有2个正整数点。


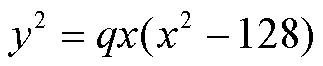


Integer Points of Elliptic Curves2=3(2-2)
DU Xian-cun, LIU Yong-hao, YU Kun-yan
(College of Teachers Education, Honghe University, Mengzi 661199, China)
It was proved that the elliptic curve in title at most have two positive integer point with the help of the properties ofcongruence and Legendre symbol.
elliptic curve; positive integral point; congruence; Legendre symbol
O156.1
A
1009-9115(2022)03-0004-02
10.3969/j.issn.1009-9115.2022.03.002
2021-10-26
2022-04-20
杜先存(1981-),女,云南凤庆人,硕士,副教授,研究方向为数论。
(责任编辑、校对:赵光峰)
