重力场中Dirac方程的非相对论近似*

郭光杰

(1.邢台学院 物理与电子工程学院，河北 邢台 054001；2.邢台学院 邢台市机器人智能检测与分拣技术研究与应用重点实验室，河北 邢台 054001)

0 引言

引力的量子效应是量子引力理论的一个引人入胜的课题，任何相关的实验或观测现象都可能帮助理论物理学家跨越广义相对论和量子力学的鸿沟.随着引力波探测技术的迅速发展，越来越多的有关黑洞的直接探测数据正在被获取[1-4].按照广义相对性原理，在引力背景下，微观粒子的运动行为应该由弯曲时空中量子力学方程描述[5-6].为了更好地理解黑洞的行为，越来越多的数值和解析算法正在被提出去求解弯曲时空中的Dirac方程[7-10].

1974年,Abbott等[1]利用晶体干涉仪观测了地球引力场对中子波长的影响，这使得人类首次在地球上观察到了引力的量子效应.但是，在很多教科书或文章中，解释该实验的理论却并未采用弯曲时空中的Dirac方程，而采用了势函数为牛顿引力势的薛定谔方程[12-13].当然，这样做也是有一些理论依据的.比如，在经典力学框架下，爱因斯坦场方程可以推导出牛顿场方程[14]，牛顿的引力势可看作弱引力场下弯曲时空的近似结果.但是，在量子力学框架下，牛顿的引力势可否也看作弱引力场下弯曲时空的近似结果呢？也就是，这两种理论对地球上引力量子效应的解释是否自洽？答案不是显然的，文献中还没有关于这一问题的论述.

内在逻辑的一致性和体系的自洽性，一直是物理理论的基本追求，也是物理理论最富魅力的原因之一.量子力学理论和时空弯曲理论都各自建立起了完整的理论，各有其适用的条件.而重力问题是这两个理论的交会点，要求这两个理论无缝连接.这两种理论在解释地球上引力场量子效应中如何实现自洽？对这一问题的解答将提供一个具体而清晰的两者自洽的物理细节，帮助建立两者自洽的物理图像.

本文在量子力学的框架体系内，利用低能近似得到了弯曲时空下Dirac方程的非相对论近似.结果表明，在量子力学框架下，引力的效应体现在得到的牛顿引力势和对动能的修正；在低能且弱引力场近似下，动能修正项和引力势相比可忽略不计.因此，在量子力学框架下重力势依然是弯曲时空的自然结果.两个理论都可解释地球上重力的量子效应，其自洽性得以说明，其物理图像得以建立.

1 重力场下中子运动的非相对论量子描述

晶体干涉仪由一块Si单晶柱制成.把它做成等间距相互平行的前、中、后三片，厚度约为几毫米，如图1所示.

入射中子束穿过前片后分为两束，即沿原入射方向的投射束和在晶面上发生布拉格衍射的衍射束.这两束穿过中片后分成四束，其中的两束在穿过后片后重新会合为一束，发生干涉.从图1中可看出，若C点比B点高，则经过ACD路径中子要比经过ABD路径中子的重力势能大，由能量守恒可得其动能较小，所以其动量也较小，由于波长与动量成反比，导致经过ACD路径中子的德布罗意波长较大.传播同样的距离，上下束的相位差为[11-12]

(1)

式(1)中假设了中子的惯性质量和引力质量相等，p为中子动量，S为平行四边形ABDC的面积，φ是平面ABDC和水平面的夹角.当转动干涉仪时，探测到的干涉强度应有周期性变化.测量结果在千分之一的精度内与理论的预言值相符，这是证明万有引力在微观领域同样适用的第一个直接的实验.

重力势在这里起到关键性的作用.若假设地球是个完美的球体，在z远远小于地球半径时，有

(2)

2 重力场下中子运动的相对论量子描述

这一部分将给出文章的主要推演过程.首先，给出弯曲空间中的Dirac方程；其次，给出Schwarzschild度规下Dirac方程的描述；最后，得到Schwarzschild度规下Dirac方程的低能近似.

2.1 弯曲空间中的Dirac方程

在一个弯曲的时空中，中子运动满足弯曲空间的Dirac方程，其度规为

ds2=g00dx02+2g0idx0dxi+gikdxidxj，

(3)

式(3)中重复指标代表求和，并且i,k=1,2,3，x0=ict.

需要说明的是，按照大多数高等量子力学和量子场论教科书采用的符号习惯，选择坐标0分量为纯虚量，以方便其计算结果和平直空间的相对论量子力学进行对比.虽然大多数广义相对论的教科书上均采用坐标0分量为实参量ct，但采用纯虚0分量依然可以建立整套广义相对论，只需稍作符号修改即可.

为保证Dirac方程的广义协变性，γ矩阵需满足

γμγν+γνγμ=2gμνI,

(4)

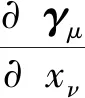
(5)

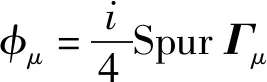
则弯曲时空中的Dirac方程[5]为

(6)

式(6)中，γμ为γμ的协变形式.和实参量ct情况一样，采用纯虚0分量依然需要区分协变、逆变张量.只是当考虑时空为平直的特殊情况时，将不再需要区分协变、逆变张量.

2.2 Schwarzschild度规下的Dirac方程

具体到地球引力场的中子，因为引力源具有球对称性，Schwarzschild度规是一个自然的选择[5].这一度规的形式为

-ds2=ζ2dx02+α2μ2(dx12+dx22+dx32),

(7)

其中，

(8)

式(8)中c为真空中的光速.下面的讨论将全部基于该Schwarzschild度规.

为满足式(4)，令

γ0=ζE0，γi=αμEii=1,2,3

(9)

式(9)中E0，E1，E2，E3满足

EμEν+EνEμ=2δμνI.

(10)

将式(9)带入式(5)，并利用式(10)和保Schwarzschild度规的仿射联络得

(11)

式(11)中：ζs=∂ζ/∂xs；μs=∂μ/∂xs；s=1,2,3；φ0，φ1，φ2，φ3由电磁势决定.把式(9)和(11)带入式(6)中得Schwarzschild度规下的狄拉克方程为

(12)

为方便下面的计算讨论，取

(13)

(14)

2.3 Schwarzschild度规下Dirac方程的低能近似

令

(15)

其中Ψa是前两个分量，Ψb是后两个分量.利用Pauli矩阵

(16)

(13)、(14)式可重写为

(17)

式(17)中I为2×2的单位矩阵.

值得注意的是，这里Pauli矩阵并未选择标准形式，并且其对易关系也不是标准形式，选择这种表示仅是为了方便符号表示4×4的E矩阵(17)，这里只关心E矩阵是否满足对易关系式(10).可以很容易计算得到E矩阵(17)确实满足(10).

问题没有涉及电磁相互作用，所以φ0=φ1=φ2=φ3=0，并且也是静场问题，则式(12)可简化为能量本征方程

(18)

式(18)中E为中子的总能量E=W+mc2，这里mc2为静止能量，在低能极限下W≪mc2.将式(15)和(17)代入上式中得

(19)

(20)

由式(19)可得

(21)

下面分析一下式(21)中各项的量纲.地球质量M=5.977×1024kg，地球平均半径r=6.371×106m，光速c=2.998×108m·s-1，引力常数G=6.67×10-11m3·kg-1·s-2[12]，则GM/2c2r≈3.5×10-10是一个极小的量，满足弱引力场近似条件，保留到一阶小量，则

(22)

(23)

另外，中子干涉实验中中子的波长λ=1.419×10-10m，这就意味着在数量级上

(24)

根据式(21)，容易看出在低能极限下，Ψa相对Ψb为小分量，近似可表示为

(25)

将式(15)代入式(20)中，可消去小分量Ψa并得到大分量Ψb满足的能量本征方程

(26)

(27)

式(27)中方程左边的第二项是对非相对论动能项的修正项，发现可忽略此修正项的条件

(28)

和由经典广义相对论得到的弱引力场的条件一致[12].对比一下这一项在不同星体表面上的数量级，如表1所示.

表1 各种典型星体表面的相对论动能修正Tab.1 Kinetic energy corrections on the surface of a variety of typical stars

显然，太阳系内的星体表面均可忽略此动能相对论修正项，而中子星这种强引力场才需考虑此修正项.在地球表面，式(27)可退化为

(29)

其中势能项恰好就是重力势.

至此，从Schwarzschild度规下的狄拉克方程出发，采用低能近似，得到了非相对论薛定谔方程，其势能项和牛顿的万有引力势一致.这个结果显示，量子力学中的重力势也是弯曲时空的自然结果.

3 结论

中子在重力场中波长的变化，是观察重力量子效应的一个典型实验，在理解量子引力理论中有着重要的意义.理论分析表明，量子力学框架下的重力势是时空弯曲的低能近似，弯曲时空的狄拉克方程可以很自然地过渡到非相对论薛定谔方程，其方程和传统方法得到的完全相同.这一结果，不但表明这两个理论是自洽性的，而且为理解两种理论如何实现自洽，建立起了清晰的物理图像.

值得指出的是，相对论下的量子力学方程不止狄拉克方程，还有克莱因高登方程以及麦克斯韦方程等.本文只研究了弯曲时空中的自旋为1/2的狄拉克方程的低能近似，那么描述其它自旋的弯曲时空量子力学方程的非相对论近似是否也能自然地得到牛顿的引力势呢？这个问题也是值得继续探讨的.