露天矿岩体力学参数对终了边坡稳定性影响敏感性数值模拟

马毓婷，陈俊智，任春芳，冯豪天，张梦原

(昆明理工大学 国土资源工程学院，昆明 650032)

在日常的矿山企业安全生产中，露天矿山的边坡稳定性作为一个关键的技术问题，长期以来一直是矿山企业关注的重点之一，同时岩石力学相关领域的学者也将其作为一个研究重点。边坡的滑坡失稳破坏对矿山企业安全生产影响极大，同时也是三大地质灾害之一[1]。得益于相关能力的提升，露天矿山企业开采高度与深度逐步加大，所形成的露天矿终了边坡高度越来越高，随之形成的就是高陡的露天矿终了边坡和深凹采场，所以对于矿山企业的安全性要更加重视。在边坡产生失稳破坏之前预先分析其安全性，将危险因素进行控制或者剔除，并评估危险的露天矿终了边坡，能够降低相应事故发生率，因此，矿山企业十分重视评估露天矿终了边坡稳定情况。对于掌握露天矿终了边坡稳定情况，现在已经有十分丰厚的成果。王旭春等[2]对于岩体边坡稳定性的研究主要是分析影响边坡稳定性的因素，分别研究了同一岩体和不同岩体的情况。宛良朋等[3]以四川省某水电站为工程实例分析了边坡稳定性评价受岩体参数的控制情况，得出该边坡的稳定评价主要依赖于凝聚力与内摩擦角共同作用。冯德润等[4]利用强度折减法来对影响露天矿边坡稳定性的岩体参数进行了相关研究。黄高峰等[5]利用有限差分法对Hoek-Brown强度准则里面不同的岩体力学参数影响边坡稳定情况的程度做了研究。周辉等[6]分析总结了岩石强度的时间效应，发现了影响岩石强度损失的因素。弥宏亮等[7]利用极限平衡法进行了边坡稳定性的三维分析，同时在工程中加以实践。翁其能等[8]利用双折减系数法对楔体滑坡的稳定情况进行了研究。任红岗等[9]利用ODE-GRA评价模型来研究采场岩体参数对采场稳定性影响的敏感性分析，其研究结果表明，在Hoek-Brown准则所考虑到的相关岩体参数中，对采场稳定性影响最大的因素是GSI。张东旭等[10]研究了岩体的抗剪强度参数如何作用于边坡稳定情况。蒲朝钦等[11]对影响层状岩质边坡稳定情况的参数敏感性进行探究。高庆辉[12]研究了不同岩体参数对露天矿安全隐患的影响。肖欢等[13]运用极限平衡法及理正软件计算分析某露天矿边坡安全系数，确定其稳定情况。

为了探究岩体的力学参数如何影响露天矿终了边坡的安全情况，可利用敏感性手段来进行考察。在进行敏感性分析时，可以采用控制变量的方法来分析露天矿边坡稳定性受岩体不同力学参数的影响，即进行计算时每次仅改变其中一个参数，将露天矿终了边坡安全系数的变化程度作为对比项，从而找出影响程度最大的参数。

1 工程概况

云南某露天矿矿石以灰岩为主，石灰岩矿层状赋存于中元古界昆阳群大龙口组，属浅海沉积的层状矿床，为露天开采矿山(图1)。矿区北部较高南部较低，为构造、剥蚀作用形成的低中山地形。矿区范围南北长0.80 km，东西宽0.20 ～ 0.80 km。矿区露天开采规模大，加之区内地质构造影响，露天开采高陡边坡岩石力学问题较为突出。

图 1 云南某矿山现状全貌Fig.1 Present situation of a mine in Yunnan

某露天矿开采完毕后形成的终了边坡高度为172 m，采场台阶数为12个，其中1 750 m平台的台阶高度为10 m，1 910 m平台的台阶高度为12 m，其他平台均为15 m，台阶坡面角为60°，最终边帮角为48°。

2 室内岩石物理力学试验

2.1 试验过程

在岩土工程稳定性研究中，各种分析软件的广泛使用让数值模拟法发展迅速。数值模拟计算中赋予岩体不同的参数，得到结果并不一致，因此确定准确的计算所需数据是研究边坡安全与否最重要的依据。对于岩体力学参数的获取，采用原位试验这种方法无疑是最准确的，但是由于试验复杂、费用高、耗时长等因素限制，大型现场原位试验这一方法的使用并不广泛，发展受限[14]。针对这一限制，可通过室内力学试验来确定相关岩石的力学参数，再将所得到的岩石力学参数通过一定的计算来获得岩体的力学参数，从而使其可以直接运用于工程实际中。

依据云南省某露天矿边坡的现场情况，采集拥有代表性的矿岩做物理力学参数的相关试验。按照现行《中华人民共和国地质矿产行业标准(DZ/T 0276.2015)》中所涉及岩石物理力学性质实验相关规范，根据不同的要求进行岩样的加工。加工试样的形状为圆柱体试件(图2)，直径与试件高度之比分别为1∶2和1∶1，其中直径为50 mm，试件高为100 mm及50 mm。待试样加工后分别对其进行抗压强度试验、变形试验、劈裂试验、变角度剪切试验。

图 2 制备试样Fig.2 Preparation of samples

抗压强度试验及变形试验，利用压力试验机测得岩石破坏时所承受的最大荷载，岩石抗压强度计算公式见式(1)。

(1)

式中，R为岩石抗压强度，MPa；P为破坏时最大荷载，kN；A为垂直加荷方向的试样面积，mm2。

变形试验和抗压强度试验(图3)同时进行，变形试验能够获得岩石的弹性模量和泊松比。在变形试验过程中给试件施加轴向压力，连接电阻应变片可以得到横向和纵向应变。岩石弹性模量计算公式见式(2)，泊松比计算公式见式(3)。

(2)

(3)

式中，E为弹性模量，MPa；μ为泊松比；σc为岩石单轴抗压强度，MPa；εx为σc对应的横向应变；εy为σc对应的纵向应变。

图3 抗压试验Fig.3 Pressure test

劈裂试验(图4)，岩石的抗拉强度是通过劈裂试验得到的。试验中的试件破坏方向一般来说与径向方向一致。岩石抗拉强度由公式(4)计算可得。

(4)

式中，σt为岩石抗拉强度，MPa；P为试件破坏时的最大压力值，N；D为试件的直径，mm；L为试件的高度，mm。

变角度剪切试验(图5)，利用变角度剪切试验法可以得到岩石的凝聚力以及内摩擦角。变角度剪切试验中，会有正应力和剪应力施加在试件上，其中剪应力与剪切方向平行，正应力与剪切方向垂直。这两种力均由模具受到的试验机所施加的荷载P分解而来，这两种力可由式(5)和式(6)计算得到。

(5)

(6)

式中，α为模具倾角，°；A为试件受剪面面积，mm2。

图5 抗剪强度试验Fig.5 Shear strength test

模具的倾角分别选用45°、50°和55°，共三个角度，每个角度4个试件。用线性回归公式将试验所获得的数据做相应计算，可以得到岩石的凝聚力c以及内摩擦角φ。具体计算见式(7)。

τ=σtanφ+c

(7)

式中，τ为剪应力，MPa；σ为正应力，MPa；φ为岩石内摩擦角，(°)；c为岩石凝聚力，MPa。

2.2 岩石力学试验结果

根据试验得出数据实验结果见表1。

表1 岩石力学试验结果

3 数值模拟

3.1 终了边坡模型的选取与建立

为了解岩体力学参数对终了边坡稳定性的影响，选取云南某露天矿中具有代表性的坡高最高的一条剖面来进行分析。

在建立终了边坡模型中，根据郑颖人等[15]的观点，设置坡高为172 m，坡脚到左边界距离为258 m，坡顶到右边界距离430 m，模型高344 m，模型宽810 m。此次模拟选用Midas GTS NX软件建立模型，利用FLAC3D进行数值模拟运算。Midas GTS NX在前期建立模型过程中操作可行性高，可以进行快速建模，把露天矿终了边坡剖面图导入软件，利用软件来完成露天矿终了边坡模型的设立，得到的模型见图6。对模型进行网格划分，其中对终了边坡附近的网格划分更加细密，模型共划分152 230个节点，198 457个单元体。FLAC3D对于分析露天矿终了边坡稳定性的模拟计算能力出众，将建立的模型导入FLAC3D进行后续数值模拟的计算，见图7。

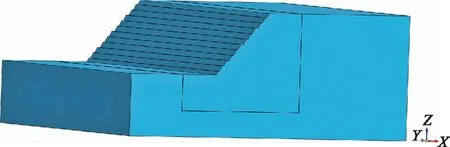
图6 终了边坡模型图Fig.6 Final slope model

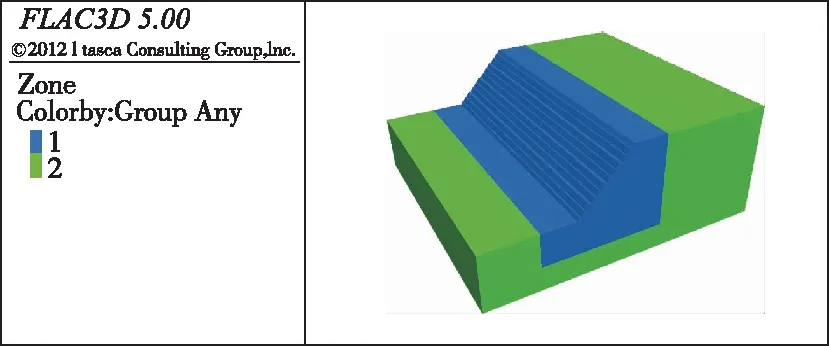
图7 三维数值模拟计算模型图Fig.7 3D numerical simulation model diagram

同时对模型作出如下假设：

1)假设模型里岩石结构是均质的、各向同性连续体。

2)不考虑水、爆破、地表地形的影响。

3)根据模型特点以及各类本构模型适用场景，此次模拟选择Drucker-Prager模型进行计算。

3.2 边界条件

FLAC3D软件中，一般来说有两种边界条件，分别是位移边界条件和应力边界条件，在讨论露天矿开采形成终了边坡这类静力学问题中可忽略水平应力影响，选择位移边界条件。沿着模型x轴方向施加x方向的约束，y轴方向施加y方向的约束，模型底部施加z方向约束，模型顶部和终了边坡为自由边界。

3.3 设置参数

取上述室内岩石物理力学试验所得到的结果，运用Hoek-Brown强度准则折减计算得到相关岩体力学参数见表2。将所得的岩体力学参数分别变化-50%、-25%、25%以及50%，所得数据见表3。

表2 折减后的岩体力学参数表

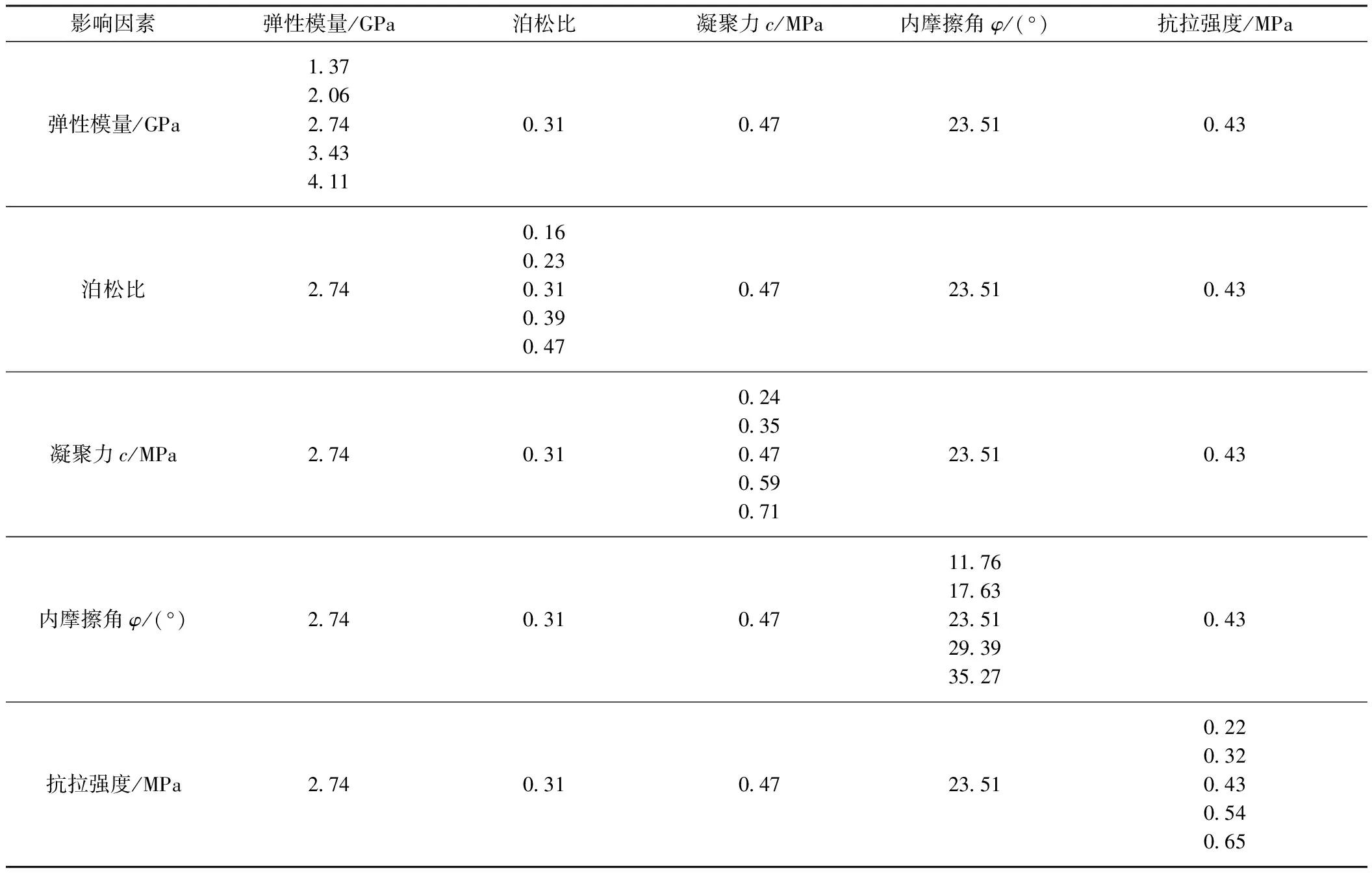
表3 设置模拟参数表

3.4 模拟结果

本次模拟采用FLAC3D软件对终了边坡模型进行计算，得到不同影响因素参数在不同组合情况下终了边坡的稳定情况。根据表2岩体力学参数计算所得边坡安全系数如图8所示。在数据选择中利用控制变量法对上述参数表中的参数进行相关组合。将计算所得不同参数条件下的终了边坡安全系数制成折线图，其中，x轴为所改变的参数，y轴为利用FLAC3D模拟计算所得安全系数，所得结果见图9～13。

图8 根据表2参数计算所得边坡安全系数Fig.8 Calculation of slope safety factor based on table 2 parameters

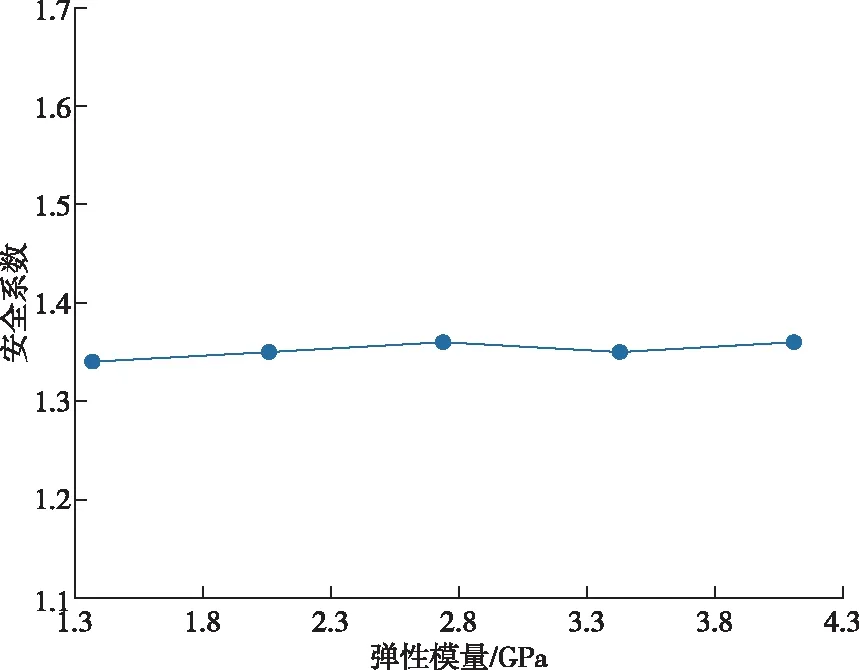
图9 仅改变弹性模量时的安全系数Fig.9 Safety factor for elastic modulus only

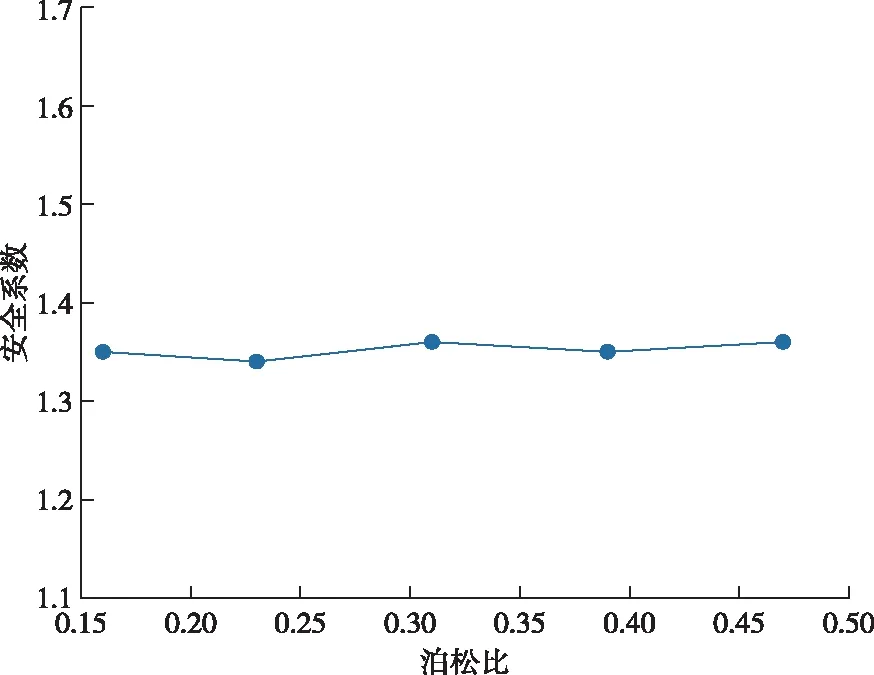
图10 仅改变泊松比时的安全系数Fig.10 Safety factor for Poisson′s ratio only

图11 仅改变凝聚力时的安全系数Fig.11 Safety factors when only cohesion changes

图12 仅改变内摩擦角时的安全系数Fig.12 Safety factor for only changing internal friction angle

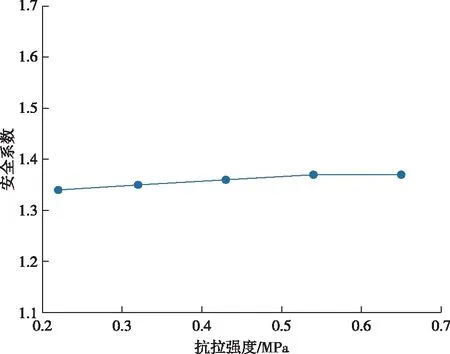
图13 仅改变抗拉强度时的安全系数Fig.13 Safety factor for only changing tensile strength

由图9可知，控制其他影响因素，只改变弹性模量时，岩体终了边坡安全系数改变量很小，折线图与x轴近似平行状态。由图10可知，控制其他影响因素，仅对泊松比的参数作出改变时，折线图的变化率很小，图线与x轴几乎平行。由图11可知，控制其他影响因素，改变凝聚力的数值时，凝聚力数值越大，终了边坡安全系数越大，即边坡越稳定，且与上述两种影响因素相比，安全系数增加幅度明显增大。

由图12可知，控制其他影响因素，对内摩擦角这一单一变量作出改变时，内摩擦角越大，边坡安全系数越大，折线图斜率与图9、图10相比有较大改变。由图13可知，仅改变抗拉强度这一单一变量，岩体终了边坡安全系数变化幅度较小。

4 结论

通过现场取石灰岩做室内岩石力学试验得到岩石相关物理力学性质，进而得到岩体力学参数。利用控制变量法研究岩体相关物理力学性质如何控制露天矿终了边坡稳定情况，得出结论如下：

1)岩体的凝聚力和内摩擦角对终了边坡稳定性影响较大，若改变凝聚力或内摩擦角，终了边坡安全系数变化较大。

2)岩体的弹性模量、泊松比以及抗拉强度影响露天矿终了边坡稳定性程度较小，仅改变弹性模量、泊松比或者抗拉强度，露天矿终了边坡安全系数改变程度比较微小。

3)考察露天矿终了边坡稳定性时着重考虑岩体力学参数里凝聚力以及内摩擦角的影响。