Ⅰ-Ⅱ型复合裂纹对脆性岩石受压破坏的影响

王体富，周宗红

(昆明理工大学 国土资源工程学院，昆明 650000)

随着对深部地下资源的需求以及地下空间的开发越来越大，诸多地下工程都面临着岩体开挖的问题，如公路隧道以及地下矿产资源的开发等，都需要掌握岩体受载后产生破坏的一系列力学问题，以此作为岩体工程的理论依据。岩石内部的细观损伤最终导致岩石整体上的宏观破坏，因此，采用脆性岩石宏-细观损伤相结合的方法研究其失稳破坏具有重要意义。目前，许多学者基于损伤力学对岩体失稳破坏进行了深入的研究，其成果得到了普遍的认可。曹文贵等[1]在损伤力学的基础上对岩石的损伤进行了重新定义，建立了围压下岩石损伤统计模型。朱其志等[2]基于热动力学理论和均质化方法从细观损伤力学的方面得到了花岗岩的非弹性应变和损伤演化的模型。杨强等[3]考虑到了岩体的损伤和塑性的耦合作用，推导出了在关联流动法则下岩体塑性损伤本构方程。袁小平等[4]基于细观力学的角度，研究了岩石微裂纹扩展的弹塑性损伤本构模型。杜修力等[5]通过岩体受载时真实应力的概念和应变等效假设，建立了岩石材料的三维弹塑性损伤本构方程，并在后续的实验中得到了验证。此外，有学者基于线弹性断裂力学来研究脆性岩石内部微裂纹对其承载力的影响，并取得了很大的成果。任利等[6]通过单个线性裂纹受到压缩荷载的剪切断裂条件，明确了岩石裂纹受到压缩荷载时张破裂纹剪切断裂韧性的物理意义以及求解方法。赵均海等[7]基于双剪统一强度理论得到了不同屈服准则和不同材料下的断裂因子，并且适用于不同的受力情况，为充分发挥材料性能提供了理论支持。

基于细观力学研究岩石受载后微裂纹的扩展、贯通直至岩石失稳破坏有着重要的意义。在岩石断裂力学中，将岩体的裂隙分为Ⅰ型裂纹(张拉型裂纹)、Ⅱ型裂纹(滑开型裂纹)、Ⅲ型裂纹(撕裂型裂纹)。并且岩石内部的裂纹并非只有一种单一类型，而是普遍存在各种裂纹相互作用的复合型裂纹。李晓照等[8]基于断裂力学的理论，研究了岩石中存在的张拉裂纹对于岩石破坏产生的重要影响，将岩石的裂纹扩展、贯通引入到岩石宏观破坏中，得到了脆性岩石的蠕变失效特性的宏-细观力学模型，但其只考虑了岩石内部存在的张拉裂纹，因此其模型存在一定的局限性。

在大多数岩土工程中，岩石内部的微裂纹扩展、贯通是在压剪复合应力下形成的[9]，且Ⅰ-Ⅱ型复合裂纹是最为普遍的[10-12]，单一裂纹的研究并不能很好地反映岩石内部裂纹对脆性岩石造成宏观破坏的影响。复合型裂纹的扩展、贯通才是岩石破坏最为关键的影响因素之一。因此，基于Ⅰ-Ⅱ型复合裂纹来研究岩石的失稳破坏有着更深的意义。邓宗才等[13]依据断裂力学得出复合裂纹最大拉应变断裂准则，但该准则较适用于混凝土材料，因此存在一定的局限性。除此之外，尹光志等[14]通过三点弯曲、四点弯曲的实验对Ⅰ-Ⅱ型复合裂纹进行了研究，得出了其断裂判据。以上研究都是针对Ⅰ-Ⅱ型复合裂纹的失稳，并没有体现出Ⅰ-Ⅱ型复合裂纹的扩展、贯通对岩石产生宏观破坏的影响。本文在前人研究的基础上，将Ⅰ-Ⅱ型复合裂纹的强度因子作了变换，得到了受裂纹初始断裂角和Ⅰ型裂纹参数影响的Ⅰ-Ⅱ型复合裂纹强度因子表达式。通过数学推导得出了含有Ⅰ型、Ⅱ型裂纹参数影响的应力与裂纹扩展的关系式σ-l，再结合损伤-应变关系推导出含Ⅰ-Ⅱ型复合裂纹参数影响的应力-应变关系式σ-ε。并在此基础上研究了Ⅰ-Ⅱ型复合裂纹的各种参数对于脆性岩石受压产生失稳破坏的影响。

1 理论模型

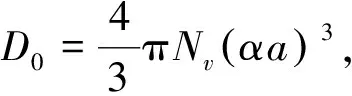
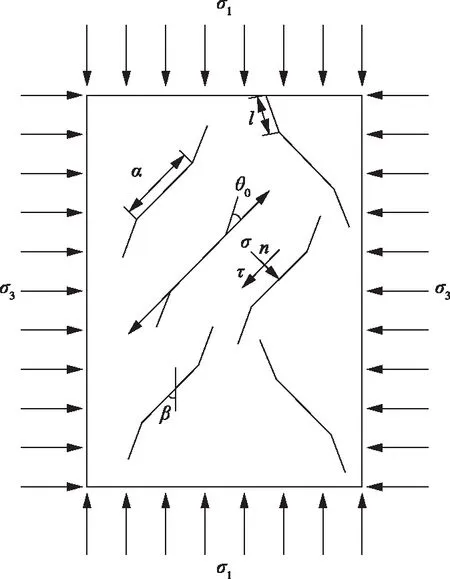
图1 三轴压应力作用下岩石微裂纹扩展模型Fig.1 crack propagation model of rock under triaxial compressive stress

在三轴压应力作用下微裂纹表面产生一个正应力σn和剪应力τ，其表达式为：

(1)

(2)

根据线弹性断裂力学理论，应力强度因子Ke要达到岩石材料本身的断裂韧度KIc时初始裂纹扩展才会发生。在此，本文忽略应力强度因子在将要达到岩石材料断裂韧度时发生的亚临界裂纹扩展，认为只有在应力强度因子达到岩石材料的断裂韧度时裂纹才会发生扩展。在拉剪复合应力作用下Ⅰ型裂纹应力强度因子KⅠ和Ⅱ型裂纹应力强度因子KⅡ表达式为[19]：

(3)

(4)

1.1 轴向应力与裂纹扩展之间的关系

在脆性岩石断裂力学中，依据最大周向拉应力准则得出了在一般情况下裂纹的失稳准则：

(5)

某种意义上可以将Ⅰ-Ⅱ型复合裂纹转化成一个等效的纯Ⅰ型裂纹，其失稳准则为：

Ke=KIc

将式(3)、(4)、(5)联立起来，得到Ⅰ-Ⅱ型复合裂纹和Ⅰ型裂纹之间应力强度因子的关系为：

(6)

脆性岩石初始微裂纹扩展后，对于纯Ⅰ型裂纹，考虑到翼型裂纹长度l，可以得到Ⅰ型裂纹应力强度因子与裂纹长度之间的关系为[19-21]：

(7)

联立式(6)、(7)，考虑裂纹长度l，得到Ⅰ-Ⅱ型复合裂纹应力强度因子表达式：

(8)

当应力强度因子达到岩石材料断裂韧度时，裂纹开始扩展，根据(8)式可以得到岩石应力状态与裂纹扩展长度之间的关系为：

(9)

式中，

X1=(1-cos2β)(1+cosθ0)(A1c1+A1c2)+3sinθ0sin2β(A1c1+A1c2)

式中，β—裂纹角，(°)。

1.2 轴向应变与轴向应力之间的关系

在工程实际中，岩石材料的强度与其自身的内部损伤机制以及流变特性是密切相关的。由于流变特性使岩石内部产生微裂隙，并且随着时间的推移，会导致裂纹的扩展，相互贯通，内部损伤进一步加大，从而使岩石的强度和弹性模量降低，对于此类效应的岩石材料，可以定义损伤演化方程为[22]：

D=1-e-mε

(10)

式中，D-损伤因子，m-实验待定参数，ε-轴向应变。

基于细观微裂纹扩展的损伤定义为[20]：

(11)

联立式(10)、(11)得到宏观损伤应变与细观微裂纹扩展长度的表达式：

(12)

联立式(12)、(9)，得到考虑了细观微裂纹扩展的Ⅰ-Ⅱ型复合裂纹岩石材料的应力-应变关系表达式：

(13)

式中，

Y1=(1-cos2β)(1+cosθ0)(A1J1+A1J2)+3sinθ0sin2β(A1J1+A1J2)；

2 结果与讨论

基于以上理论，得到本文模型的应力-应变关系曲线，并通过大理岩的常规三轴实验结果来验证本文研究的合理性。此外，着重研究了岩体内部的初始损伤、裂纹间摩擦系数以及翼型裂纹长度对岩石应力-应变关系的影响，其中具体参数选取如下：

在岩石受压过程中，认为达到裂纹临界应力σc时翼型裂纹才开始扩展，临界应力与裂纹间摩擦系数和裂纹尺寸的关系为[7]：

(14)

2.1 应力-应变关系

基于(13)式(D0取0.032)，得到了应力-应变关系曲线。大理岩在高地应力的情况下会表现出脆性向延性转化，本文模型在一定围压范围内充分表现出了这一特点。图2中，岩石应力起初有一个上升，在到达应力峰值后岩石应力开始下降，并且随着围压的增大，岩石的承载力也增大。本文通过一种均匀化思维对岩石的应力-应变关系进行简化，无法准确地描述岩石应变的局部化失效，是以全局化整体失效来进行岩石破坏的分析，进而研究Ⅰ-Ⅱ型复合裂纹参数对岩石承载力的影响。因此，该模型得出的应力-应变曲线趋势与图3常规三轴实验结果相似，并且在数值上有一定的可比性，表明了该模型具有一定的合理性。

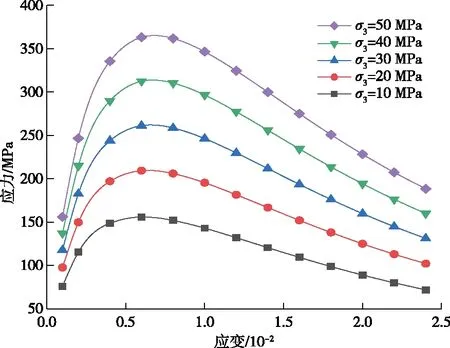
图2 不同围压下的模型轴向应力-应变关系曲线Fig.2 Axial stress-strain curve of the model under different confining pressure

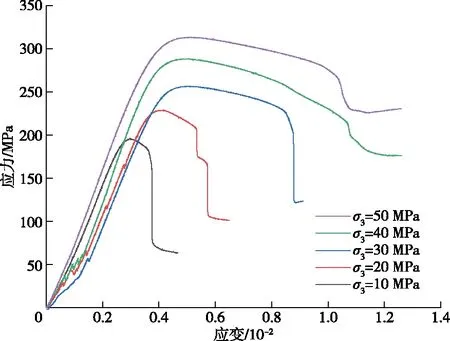
图3 常规三轴实验全过程应力-应变关系曲线Fig.3 stress-strain relationship curve in the whole process of conventional triaxial experiment

2.2 裂纹参数对岩石应力-应变关系的影响

2.2.1 裂纹初始损伤对岩石应力-应变关系的影响

在自然状态下，岩石受到地应力等诸多因素的影响，其内部会产生初始损伤，这些初始裂纹损伤对于岩石的承载能力有着较大的影响。

在图4中可以看出，在围压一定时，当轴压在210 MPa以下时，初始损伤对于岩石承载能力的影响并不大，而随着压力的增加初始损伤对于岩石承载能力的影响逐渐明显，这是由于在微裂纹的发展过程中岩石受压达到临界应力时，裂纹才能产生失稳破坏，在此之前，岩石承载能力受初始损伤的影响很小。图5中，在相同初始损伤量时，围压越大岩石的峰值应力越大。相同围压条件下，岩石的峰值应力随着初始损伤的增大而减小，在围压为30 MPa时，当初始损伤量为0.01的岩石峰值应力约为299 MPa，初始损伤量为0.07的岩石峰值应力约为101 MPa，相比减小了约66.2%，并且围压越大，岩石应力峰值受初始损伤量的影响越敏感，因此在深埋岩体工程中，应适当减少工程扰动对于岩体承载能力的破坏。

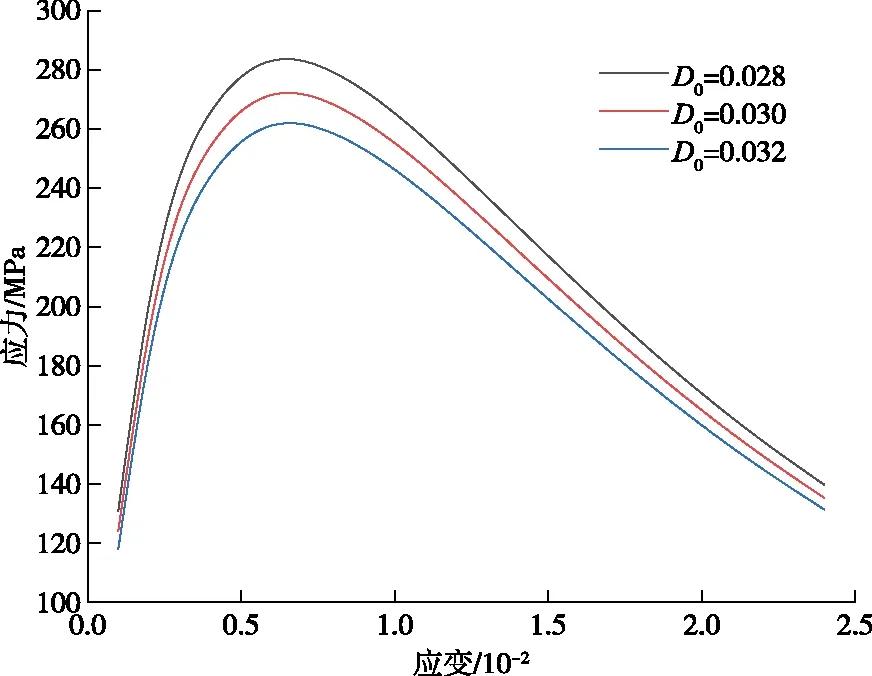
图4 围压30 MPa下不同初始损伤对岩石应力-应变关系的影响Fig.4 Effect of different initial damage on the stress-strain relationship of rock under confining pressure 30 MPa

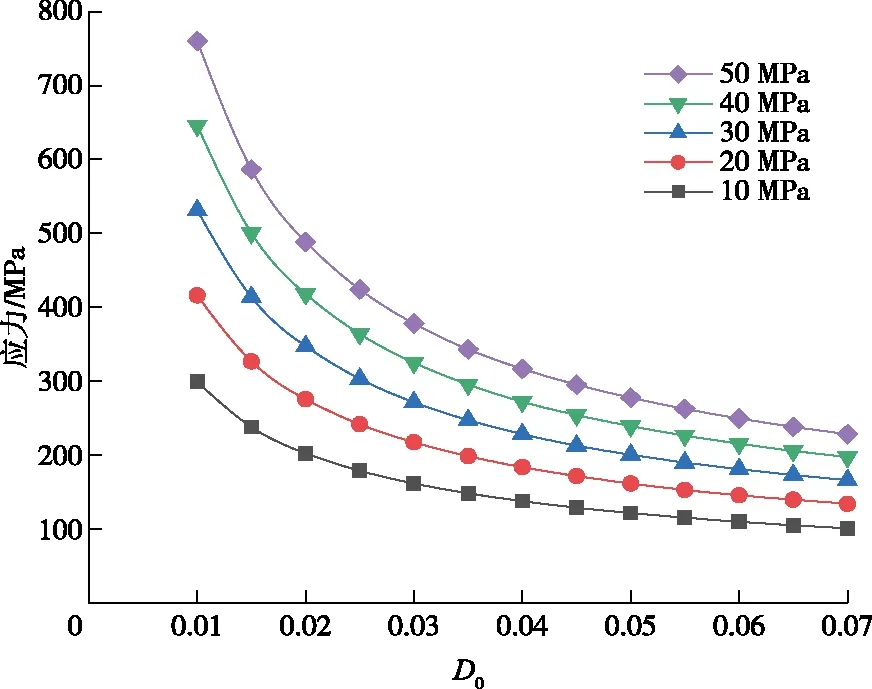
图5 不同围压下初始损伤对峰值应力的影响Fig.5 Effect of initial damage on peak stress under different confining pressure

2.2.2 初始裂纹尺寸对岩石应力-应变关系的影响

基于(13)式，在围压50 MPa条件下，分析不同裂纹尺寸对于岩石应力-应变关系的影响。通过图6可以看出岩石应力-应变关系随初始裂纹尺寸的变化而变化，在相同的应变条件下随着初始裂纹尺寸的增大岩石的承载能力降低。裂纹尺寸为1 mm时应力峰值约为400 MPa，当裂纹尺寸为5 mm时应力峰值只有约320 MPa，应力峰值下降了约20%。

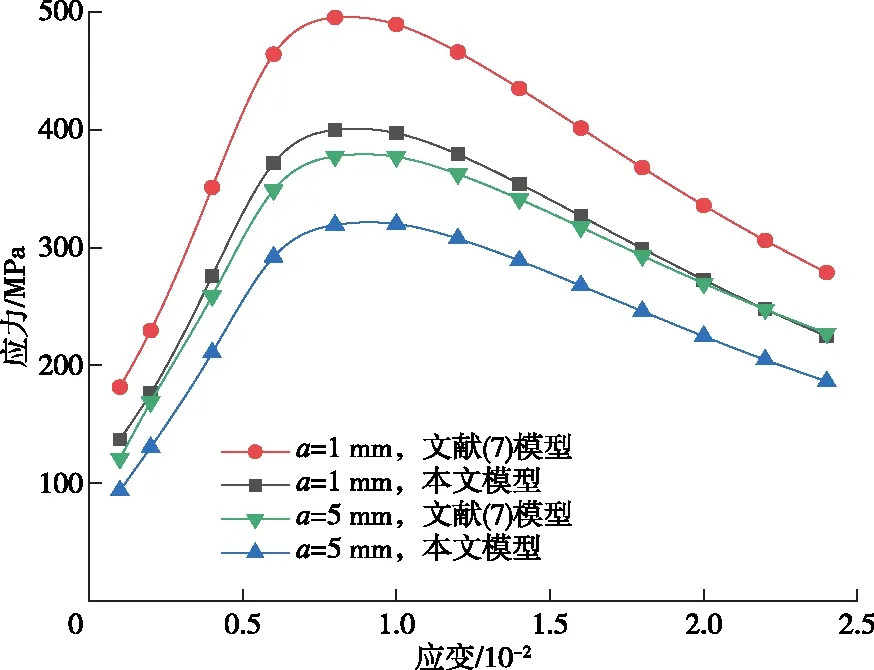
图6 围压50 MPa下初始裂纹尺寸对岩石应力-应变关系的影响Fig.6 Effect of initial crack size on stress-strain relationship of rock under confining pressure 50 MPa

2.2.3 裂纹间摩擦系数对岩石应力-应变关系的影响

基于(13)式，在围压50 MPa条件下，分析裂纹间不同摩擦系数对于岩石应力-应变关系的影响。通过图7可以看出，在相同应变量的情况下，随着裂纹间摩擦系数的增大，轴向应力也随即增大。裂纹间摩擦系数为0.5时，应力峰值约为549 MPa，当裂纹间摩擦系数为0.1时，应力峰值达到了约342 MPa，应力峰值下降了约37.7%。由此可见，裂纹间摩擦系数的降低，使得提高岩石的承载能力也大幅降低。此外，对比文献[7]模型，在不同的裂纹尺寸以及不同裂纹间摩擦系数条件下本文模型得出的岩石承载能力都相对较小，这也印证了相较于考虑单一的纯Ⅰ型裂纹(文献[7])，岩石承载能力受Ⅰ-Ⅱ型复合裂纹参数的影响较大。

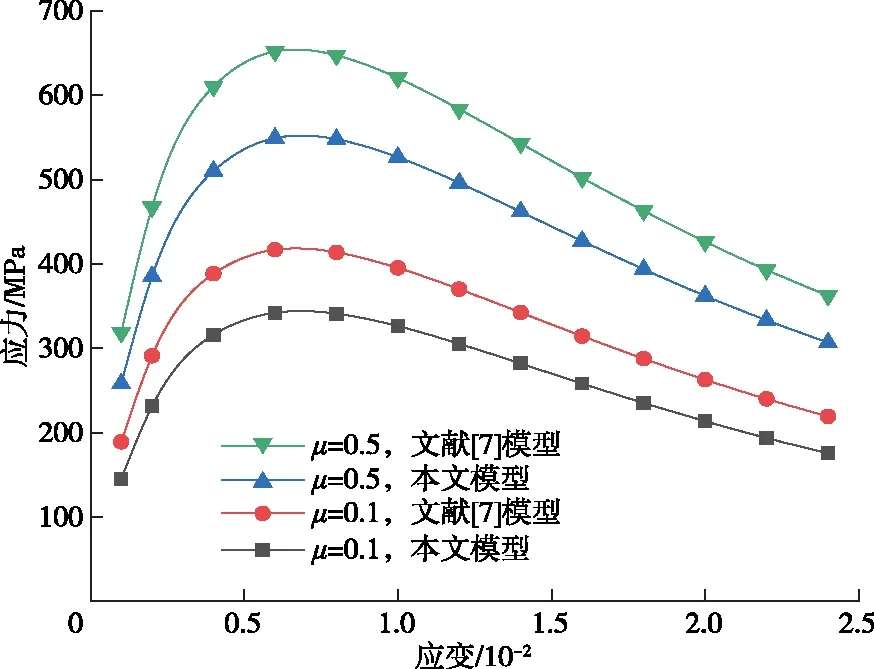
图7 围压50 MPa下裂纹间摩擦系数对轴向应力-应变关系的影响Fig.7 effect of friction coefficient between cracks on axial stress-strain relationship under confining pressure 50 MPa

2.2.4 翼型裂纹长度对岩石应力-应变关系的影响

基于(9)式得到了图8岩石在不同围压下裂纹的扩展与轴压的关系。从中可以看出在相同的轴压下，随着围压的增加，裂纹的扩展变得困难，由此可见，围压在一定程度上遏制了裂纹的扩展。并且，在围压相同时，随着裂纹的扩展轴向应力先呈现出上升的趋势，到达应力峰值后，随着裂纹进一步的扩展，轴向应力逐渐减小，出现这种情况是因为岩石受压之初裂纹开始萌生，随着应力逐渐增加，裂纹开始进一步扩展、贯通，到达应力峰值后，岩石内部损伤加大，岩石承载能力下降，直至破坏。

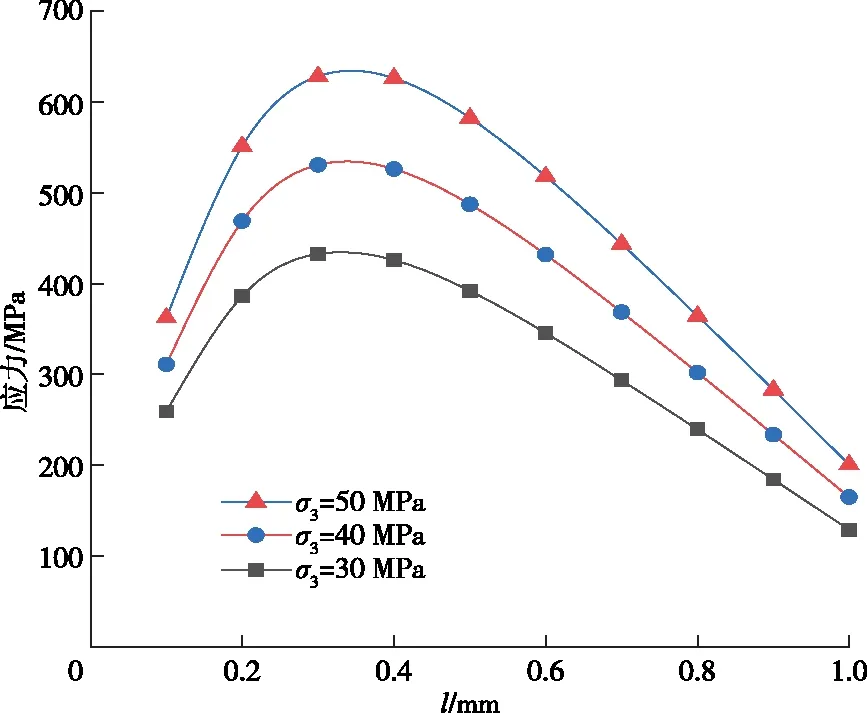
图8 不同围压下翼型裂纹长度与轴压的关系Fig.8 relationship between crack length and axial pressure of airfoil under different confining pressure

3 结论

本文基于损伤力学和岩石断裂力学研究了脆性岩石内部Ⅰ-Ⅱ型复合裂纹的扩展、贯通对于岩石承载能力的影响，将岩石受载后的宏细观表征结合起来，推导出了脆性岩石受Ⅰ-Ⅱ型复合裂纹参数影响的应力-应变关系式。在考虑到裂纹开裂角的前提下，研究了岩石的破坏受裂纹尺寸、裂纹间摩擦系数以及翼型裂纹长度的影响，对于从细观机制方面研究岩石受压产生失稳破坏提供了一定的参考。具体结论如下：

1)细观裂纹在岩石达到起裂应力时开始扩展，扩展到一定程度后，岩石应力达到峰值，随着裂纹的继续扩展、贯通，岩石的应力下降。此外，不同的围压导致岩石应力-应变关系曲线有所不同，随着围压的增大，岩石的承载能力上升，从细观机制的角度可以解释为围压的增大限制了裂纹的发展，宏观上表现为岩石的承载能力增大。

2)在相同围压下，随着围压增大，裂纹的长度减小，验证了增大围压能够遏制岩石内部裂纹的扩展、贯通。岩石的承载能力随着内部的裂纹尺寸的增大而减小，其中裂纹尺寸从1 mm增加到5 mm时应力峰值下降约20%。此外，裂纹间的摩擦系数也有着较大的影响，在相同围压下，裂纹间摩擦系数从0.5下降到0.1时，应力峰值下降了约37.7%。裂纹间摩擦系数减小，大大降低了岩石的承载能力。