宋式木构架滞回性能数值模拟与试验验证

孟宪杰，李铁英，王志华，刘 晖

(1.太原理工大学 a.土木工程学院，b.机械与运载工程学院，太原 030024；2.山西建设投资集团有限公司 博士后科研工作站，太原 030032)

在中国古代，木结构被广泛用于宫殿、庙宇、亭榭或普通住宅，这些建筑是中国历史、文化、文明以及古人智慧的集中体现。古建木结构因其特有的柱脚、榫卯及斗拱构造而表现出卓越的抗震性能，然而长期的人为和环境影响导致现存木结构明显残损，并已显著影响其继续抵抗外部荷载，尤其是抵抗地震作用的能力，因而必须采取有效的抗震加固措施以保证现存古建筑木结构免遭地震破坏。由于木结构在古时主要是木匠依经验建造，虽然留存有详细的建造方法，但对其抗震承载机理缺乏科学的认知。因而，众多学者针对古建木构架的抗震性能开展了系列研究，并取得了显著的成果。

LI et al[1]对双跨梁柱木构架进行了拟静力测试，结果表明以燕尾榫连接的木构架有较好的延性及耗能能力；潘毅等[2]建立了燕尾榫节点的数值分析模型及双折线多参数弯矩-转角力学模型，并指出燕尾榫节点主要在榫头处产生挤压变形；CHEN et al[3]完成了宋式梁-柱-斗拱足尺木构架的拟静力测试，揭示了古建木结构耗能弱而变形强的特性；谢启芳等[4-6]、薛建阳等[7]分别对整体木结构缩尺模型进行了动力测试；杨娜等[8]以典型的明清古建木结构为研究对象，对结构进行了地震易损性分析；张锡成等[9]采用ANSYS软件建立了宋式木构架的空间杆系有限元模型，并进行了动力时程分析，研究了结构的柱脚滑移倒塌和柱架层间倒塌机制；王娟等[10]采用ABAQUS软件对唐代某殿堂型一榀木构架开展了水平反复加载测试，研究了木构架的变形特征、滞回特性、刚度特征及耗能特性；万佳[11]研究了水平加速度作用下古建木构架的动力响应，指出木构架有静止、滑移、摇摆和滑移摇摆4种初始运动状态，并理论分析了以上4种运动状态的判定条件以及影响木构架初始运动状态的因素。YEO et al[12]对叠斗式木构架的水平往复加载测试表明，柱架摇摆是此类木结构的主要变形特征；SUZUKI et al[13]以日本木结构古建筑为研究对象，进行了梁-柱-斗拱木构架模型的拟静力和动力测试，结果表明木构架变形能力强，结构在小变形情况下的恢复力主要来自于柱架的摇摆。

综上所述，已有研究从理论分析、模型试验和数值模拟等方面对古建木构架的抗震性能开展了大量的工作。对木构架进行模型试验能较直观、准确地反映结构的实际变形和承载性能，但试验成本高、开展难度大，而目前对整体木构架的模拟分析普遍缺乏相应的试验验证。本文以课题组已开展的1∶2宋式梁-柱-斗拱整体木构架模型试验为基础，对该模型进行实体建模及水平往复加载模拟，对比分析了数值模拟结果的适用性及局限性。

1 有限元模型及测试

1.1 模型概况

课题组对参照《营造法式》制作的1∶2七等材梁-柱-斗拱木构架模型进行了三级不同竖向荷载下的水平往复加载测试[14]，模型如图1(a)所示，模型采用俄罗斯进口樟子松制作，木材密度466 kg/m3，含水率9.4%.参照该试验模型，采用ABAQUS软件建立了如图1(b)所示的数值分析模型，模型主要构件尺寸见表1.试验测试中，木构架柱脚直接搁置于混凝土地面上形成平摆浮搁的连接。与试验测试相同，所建立的数值模型直接放置于刚性底板上，刚性底板下表面固接，上表面与模型柱脚摩擦接触。屋顶荷载用质量板模拟，其参数与试验测试所用混凝土板(C30混凝土)一致，质量板放置于素枋上，两者之间不设任何连接。实际木构架在装配过程中榫头和卯口间存在缝隙，本次模拟在榫头两侧分别设置0.5 mm的缝隙，该缝隙大小与试验模型中的缝隙一致。

图1 木构架模型图Fig.1 Timber structure model

表1 模型主要构件尺寸Table 1 Sizes of main components of the model

1.2 材料本构关系

已有试验结果表明，木构架在水平往复荷载作用下，仅有部分横纹受压木构件易产生塑性变形，而顺纹受压构件基本处于弹性变形状态[14]。因而，本次数值模拟中顺纹受压构件仅考虑弹性变形，横纹受压构件考虑其弹性段后的应变硬化。木材弹性变形阶段的力学参数列于表2，表中弹性模量和剪切模量为试验模型所用木材樟子松的实测值，泊松比取值参考文献[15].木材横纹受压塑性变形按真实应力(σtrue)和累积塑性应变(εpl)关系考虑。根据樟子松横纹受压测试得到名义应力(σnom)和名义应变(εnom)，由式(1)和式(2)分别转化为为真实应力(σtrue)和真实应变(εtrue)，并进一步拟合得到如图2所示的真实应力和累积塑性应变关系曲线，εpl根据式(3)计算，式中εel为弹性应变，图中A，B，C三点的坐标分别为(0，3)，(0.44，11)和(0.5，53).

表2 木材弹性常数Table 2 Elastic constants of wood

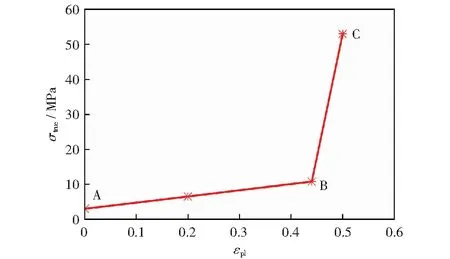
图2 累积塑性应变-真实应力关系曲线Fig.2 Curve of relationship between σtrue and εpl

σtrue=σnom(1+εnom) .

(1)

εtrue=ln(1+εnom) .

(2)

εpl=εtrue-εel.

(3)

1.3 接触及边界

模型网格单元采用八节点线性减缩积分单元C3D8R，根据构件受力特点及尺寸分别采用10～40 mm网格尺寸，对于受力和变形集中的区域如榫卯节点区，采用较小的网格尺寸。木构架中各木构件通过各类榫卯接口搭接在一起，构件面与面之间通过摩擦接触传递荷载。构件间的接触包括法向作用和切向作用两部分，其中法向作用采用硬接触，即两接触面间的压力小于等于零时便分离；当两构件产生接触时，其间的作用力以库伦摩擦模型表征，即采用摩擦系数表征接触面间的摩擦行为。课题组已参照文献[15]中木材摩擦系数的测定方法，对试验木材樟子松进行了端面与端面、径面与径面、弦面与弦面、端面与径面、径面与弦面及弦面与端面间的摩擦系数测试，本文模拟分析中木构件间的摩擦系数取上述6组测试结果的均值0.45.此外，柱脚与底板间的摩擦系数参照文献[16]中古建筑木结构柱底与础石间摩擦系数的建议值取0.6.

1.4 加载测试

数值模拟采用与试验测试相同的加载制度，竖向荷载分别采用15 kN，30 kN和45 kN三个级别，这三级竖向荷载通过对质量板设置不同的密度实现。每级竖向荷载下都按如图3所示的曲线进行8次水平往复加载测试，水平加载通过位移控制，加载点位于质量板中点，加载幅值分别为10，20，30，40，50，60，70和80 mm.

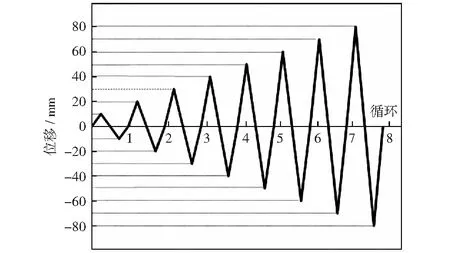
图3 加载曲线Fig.3 Loading curves

2 结果与讨论

2.1 变形特征

如图4所示，数值模拟中木构架整体变形与试验测试结果一致，水平往复荷载作用下结构变形主要表现为柱架层的摇摆，斗拱层及其上部的质量块均接近整体平动，斗拱节点各构件无明显相对滑移，表现出较好的整体性；榫卯节点有拔榫现象，但不致产生脱榫破坏(图5)，榫卯节点的转动能力保证结构在产生较大变形的同时，各木构件不产生明显损伤，即使加载至本次测试最大水平位移处，所有木构件均还可继续承载，预测结构的最终破坏形态为整体性倾覆破坏；柱脚在水平往复荷载作用下重复抬升和归位(图6)，未见滑移，与试验结果吻合；此外，数值模拟和试验结果均表明柱顶与普拍枋接触面是易产生塑性变形的区域(图7)，主要是由于柱倾斜时柱边缘的嵌压所致。

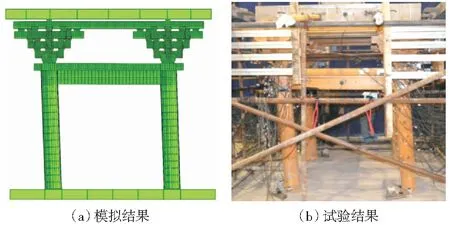
图4 整体木构件变形对比Fig.4 A comparation of the deformation of timber structure

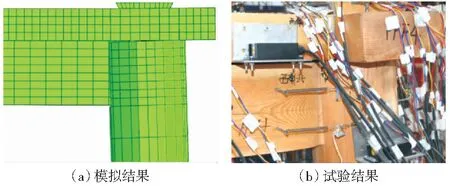
图5 榫卯节点变形对比Fig.5 A comparation of the deformation of mortise-tenon joint

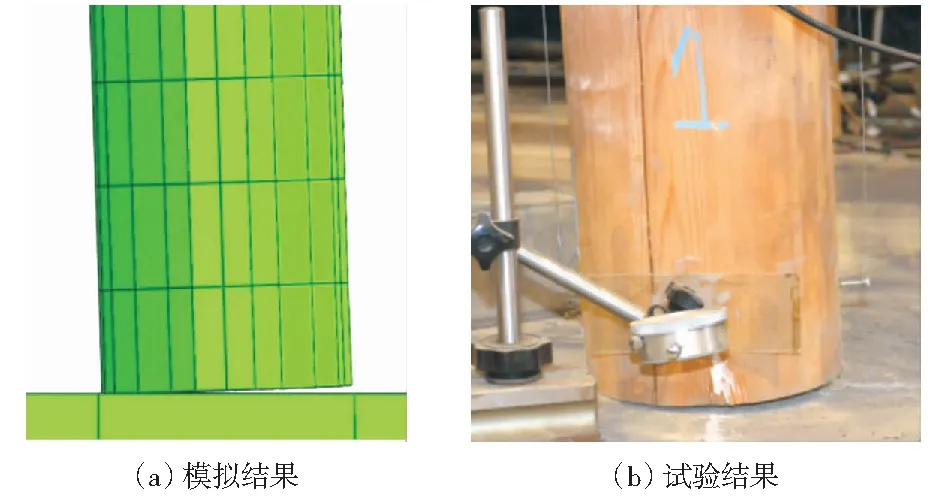
图6 柱脚变形对比Fig.6 A comparation of the deformation of column foot

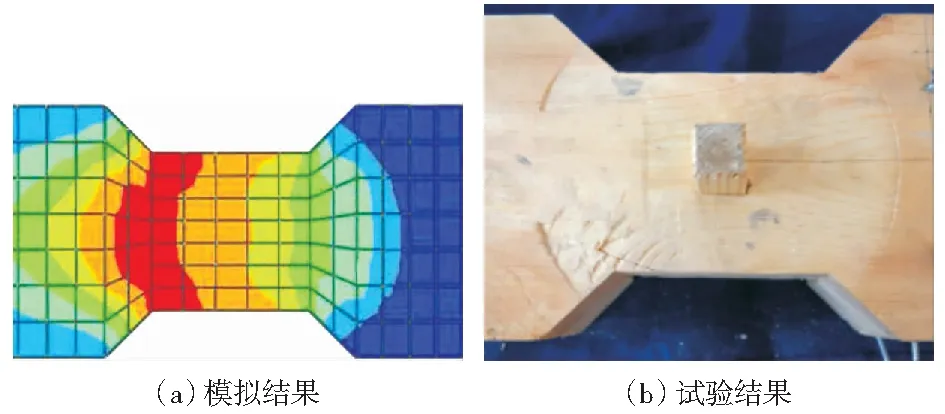
图7 普拍枋应力分布和变形区域对比Fig.7 A comparation of the stress distribution area and deformation area of pupaifang

2.2 滞回曲线

如图8所示，数值模拟与试验测试得到的木构架滞回曲线整体上相似，均呈端部饱满、中间捏缩的S型，符合摇摆结构的特征，但两者在结构不同变形阶段都表现出一定的差异。对比试验结果，数值模拟结果有以下特点：

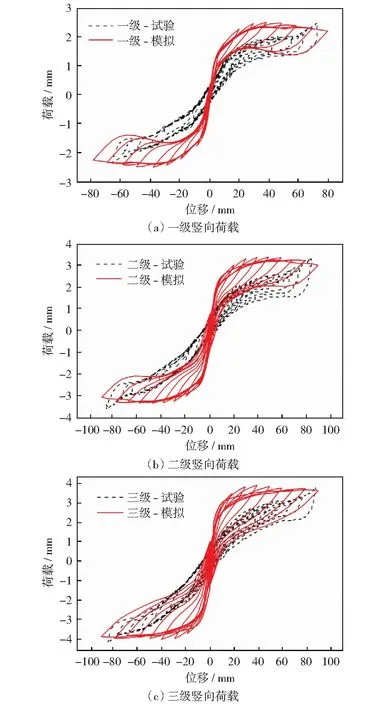
图8 滞回曲线Fig.8 Hysteresis curves

1) 当-10 mm≤Δ≤10 mm时(Δ为水平位移)，数值模拟曲线相对于试验曲线有更明显的捏缩，主要是由于数值模型未能完全反应实际结构中木构件的缺陷及构件间的各类缝隙，因而在完全卸载后结构更易恢复至初始位置；此外，数值模拟中结构在弹性变形阶段仅通过构件间少量的摩擦滑移耗能，而实际结构由于构件安装不到位，初始加载过程中个别构件也会产生少量塑性变形。

2) 当水平加载位移超过10 mm后，木构架屈服，曲线变得平缓；在加载位移达到50 mm前，数值模拟曲线均位于试验曲线之上，并且两者接近平行；当加载位移超过50 mm，数值模拟曲线平缓并略有下降，而试验曲线却小幅上升，进而也导致两者曲线逐渐靠近。

3) 竖向荷载增加使滞回曲线变得饱满，然而试验曲线无论是加载还是卸载阶段，其变化趋势均不受竖向荷载的影响，而随竖向荷载增大，数值模拟曲线在卸载阶段产生明显的差异。

4) 试验测试中，虽然测试模型和加载装置设计为完全对称，但由于构件安装不到位、水平荷载不完全对等及木材材性的离散导致滞回曲线正负方向不完全对称，而数值模拟可完全避免上述因素的影响，所得到的曲线有较好的对称性。

2.3 骨架曲线

木构架骨架曲线由每级循环的极值点相连得到。如图9所示，数值模拟与试验骨架曲线整体变化趋势相近。Δ≤10 mm时，结构处于弹性阶段，具有较大的抗侧刚度，此阶段骨架曲线为陡峭的直线，水平荷载与位移接近线性增长；之后，随着水平位移增大，结构进入屈服阶段，抗侧刚度下降，曲线逐渐变得平缓，曲线特征为位移增长较快而荷载小幅提高；进一步加载，水平外荷载基本不再变化，而变形却持续增大，但是直到最大位移处，结构层间位移角达到1/23，荷载也没有突然下降，说明木构架有相当好的延性。

图9 骨架曲线Fig.9 Skeleton curves

然而，数值模拟与试验曲线也表现出一定的差异。数值模拟中弹性阶段结构的刚度明显大于试验结果，主要是由于数值模型仅考虑榫头与卯口间的缝隙，其它各构件均完全贴合，相对于试验模型有较大的初始抗侧刚度；此外，试验测试中，屈服阶段过后，水平荷载随结构变形增大还有小幅提升，这也是由于实际结构中存在大大小小的缝隙，在较大的结构变形下，这些缝隙才逐渐闭合，构件相互接触挤压，为结构提供承载力。

从水平承载力来看，一级至三级竖向荷载下，数值模拟中的最大水平荷载分别为2.52 kN、3.41 kN和4.05 kN，相应的试验结果分别为2.50 kN、3.45 kN、3.97 kN，两者相差不到5%，因而数值模拟完全能够反映木构架的实际承载能力。

2.4 刚度

木构架刚度按式(4)计算，式中+Fi和-Fi分别表示第i次循环正、负方向极值荷载；+Δi和-Δi分别表示与+Fi和-Fi相对应的水平位移。

(4)

图10所示刚度曲线表明，木构架刚度随水平变形增大有明显的下降，并且数值模拟结果与试验结果逐渐趋近。与钢结构、混凝土结构刚度退化机理不同，木构架刚度变化一方面源自于木构件间各接触面的变化，如柱倾斜导致的柱脚和柱顶接触区域的变化、梁柱节点转动导致的榫头和卯口接触面的变化等，这也是导致木结构刚度变化的主要原因；另一方面则由构件塑性变形的累计所致。由于数值模拟中木构架变形与试验结果一致，因而两者的刚度曲线变化趋势相同。

图10 刚度曲线Fig.10 Stiffness curves

Δ≤30 mm时，数值模拟结果明显高于试验结果，并且随着竖向荷载的增大，两者间的差距进一步增大，但随着水平变形增大，模拟曲线表现出更明显的下降。此阶段木构架刚度变化最为显著，这是由于结构未变形时，柱脚和柱顶为全截面受压，结构整体处于稳定状态，有较大的初始抗侧刚度；结构产生水平变形后，柱脚和柱顶接触面逐渐向截面边缘偏移，木构架由初始的稳定状态逐渐变为可绕柱脚转动的不稳定状态，从而导致抗侧刚度明显下降，并且在此阶段内柱端受压截面减小最为显著。

当30 mm<Δ≤60 mm时，木构架中部分木构件相互接触并挤压或嵌压，延缓了结构刚度下降的速率，并且数值模拟结果逐渐接近试验值。

当Δ>60 mm时，木构架刚度基本不再下降，并且相同竖向荷载下的两组曲线基本重合，表明数值模拟结果在此阶段内可完全反应实际结构的刚度特征。在较大的水平变形下，榫卯节点由转动而产生的咬合力是影响结构刚度变化的主要因素，咬合力的增加也限制了结构刚度的进一步降低，数值模拟完全反应了木构架这一特性。

2.5 耗能

木构架的耗能能力可由等效黏滞阻尼系数(he)表征，其值按式(5)计算。式中，Sloop代表滞回环所包围的面积；SΔ表示由原点、荷载极值点及其对应的位移坐标围成的三角形面积；+和-分别表示正负加载方向。

(5)

从图11可以看出，数值模拟中，木构架等效黏滞阻尼系数随水平位移增大而增大，说明结构的耗能能力逐渐增强，该变化趋势与唐代殿堂型整体木构架数值模拟结果[10]相同，并且两者数值非常接近，均在0～0.15之间；当Δ>20 mm时，随着竖向荷载变化等效黏滞阻尼系数有了明显区分，竖向荷载增大明显增加了结构的耗能能力。然而，试验测试中，木构架在初始加载阶段耗能能力相对较高，而随着水平位移增大，耗能能力逐渐降低，并且与竖向荷载无明显的相关性，这与数值模拟结果有明显的差异。由于木材材质软，并且木构件加工过程中表面不可能完全平整，在初始侧移中构件某些位置会产生塑性变形，而在数值模拟中未考虑该因素，初始加载时木构件仅产生弹性变形；此外，数值模拟中木构件完全贴合，也使其在后期加载过程中更易累积塑性变形，耗能能力提升更显著。

图11 等效黏滞阻尼系数曲线Fig.11 Curves of equivalent viscous damping coefficient

本次数值模拟木构架等效黏滞阻尼系数在0.027～0.137之间，相应的试验结果在0.110～0.061之间。一级至三级竖向荷载下，数值模拟结果平均值分别为0.059，0.069，0.081，相应的试验结果平均值分别为0.071，0.075，0.066，两者分别相差-17.4%，-7.6%，22.9%(负值表示低于试验值)。可以看出，尽管两者曲线变化趋势有差异，但数值模拟在一定程度上也能反映出实际结构的耗能能力。

3 结论

1) 水平往复荷载作用下木构架主要变形特征为柱架层摇摆，节点变形表现为柱脚抬升和榫卯转动，数值模拟可在一定程度上反映实际结构变形特征。

2) 数值模拟能较好的体现木构架耗能能力弱而变形能力强的滞回特性，并可用于预测木构架的承载力和变形能力。

3) 随着水平位移增加木构架刚度明显降低，但下降速率逐渐变缓；水平位移较小时，数值模拟得到的木构架刚度值偏高，但水平位移较大时，数值模拟结果与试验结果接近。

4) 数值模拟与试验测试得到的木构架等效黏滞阻尼系数在变化趋势上有明显差异，但在数值变化范围上两者相近，数值模拟可一定程度上反映实际木构架的耗能能力。

5) 本次研究表明数值模拟结果虽然能较好地反应水平荷载作用下整体木构架的变形特征，然而模拟分析所考虑的木材材性与实际木材的生物特性还有较大的差别，并且无法完全考虑实际木构件的初始缺陷及安装误差，导致木构架滞回特性与试验结果存在差异。为得到更准确的模拟分析结果，需进一步优化木材本构关系模型，并且建模过程中应考虑木构件本身的缺陷特征。