多因素优化700 ℃四角切圆锅炉烟温偏差模拟

周长鑫，刘建全，武振新，苏 统，胡伟晨，孔 争

(1.上海电力大学 能源与机械工程学院,上海 201306；2.上海锅炉厂有限公司,上海 200245)

0 引 言

目前我国电站仍广泛使用燃煤锅炉进行发电和供热[1-2]。其中大多数燃煤锅炉采用煤种适应性强、炉内火焰充满度良好、煤粉颗粒停留时间长、燃尽率高的四角切圆燃烧方式[3-4]。燃煤发电会污染环境，在实现“双碳”目标的大形势之下，亟需开发新型清洁高效的燃煤发电技术[5-7]。700 ℃超超临界燃煤发电技术机组蒸汽参数：主蒸汽压力36 MPa、主蒸汽温度700 ℃、一次再热蒸汽温度720 ℃、二次再热蒸汽温度720 ℃，燃煤发电机组效率达52.5%，高于国内的超超临界机组效率5%左右[8-10]；同时700 ℃超超临界机组的供电煤耗可降低25 g/kWh，NOx与COx的排放量降低15%左右[11-12]。由于电站锅炉四角切圆燃烧方式普遍存在热偏差问题，严重情况下热偏差达200 ℃左右，极易导致锅炉内部过热器、再热器等管屏结构发生超温爆管[13-15]，且锅炉内部存在的热偏差问题会随锅炉蒸汽等参数的升高而更加严重[16-18]。

随计算机技术发展，利用CFD模拟锅炉燃烧，可在保证准确性的基础上节省成本，因此应用广泛[19-22]。郭岸龙等[4]、龙敦武等[13]、PARK等[20]对四角切圆电站锅炉模拟进行研究，认为对燃尽风进风角度进行一定程度的水平反切可有效缓解四角切圆锅炉炉膛出口存在的烟温偏差问题。姚志鹏等[17]、刘基昌等[21]对电站锅炉进行数值模拟研究，结果表明，在燃尽风进风角度合理水平反切的基础上，对左、右两侧燃尽风进风的速度进行偏置，可进一步降低四角切圆锅炉炉膛出口的烟温偏差；YAO等[22]根据正交试验法设计3因素、3水平的正交试验表(L9(34))，研究了700 ℃四角切圆锅炉烟温偏差问题，通过极差分析法与权矩阵分析法确定正交试验中3个因素对四角切圆锅炉炉膛出口截面烟温偏差影响的重要性顺序。

相比以往学者利用单因素进行烟温偏差研究，笔者采用具有交互作用的正交试验法对1台660 MW的700 ℃ Π型四角切圆锅炉进行数值模拟，设计L8(27)正交试验表，在因素可能存在交互作用的条件下分析正交试验中各因素及对应水平对炉膛出口截面烟温偏差的影响程度，同时分析各因素与水平对炉膛出口截面烟温偏差影响的权重占比。

1 研究对象

数值模拟的研究对象为700 ℃的660 MW四角切圆锅炉(上海锅炉厂设计)。四角切圆锅炉具体的三维模型结构如图1所示，锅炉炉膛宽度18.816 m、深度16.800 m、高度63.290 m。其中P1为一次风截面(Z=18.992 m)，P2为二次风截面(Z=26.432 m)，P3为燃尽风截面(Z=34.000 m)，P4为水平烟道截面(Z=55.000 m)，P5为炉膛中心纵截面(Y=9.408 m)，P6为炉膛出口截面。

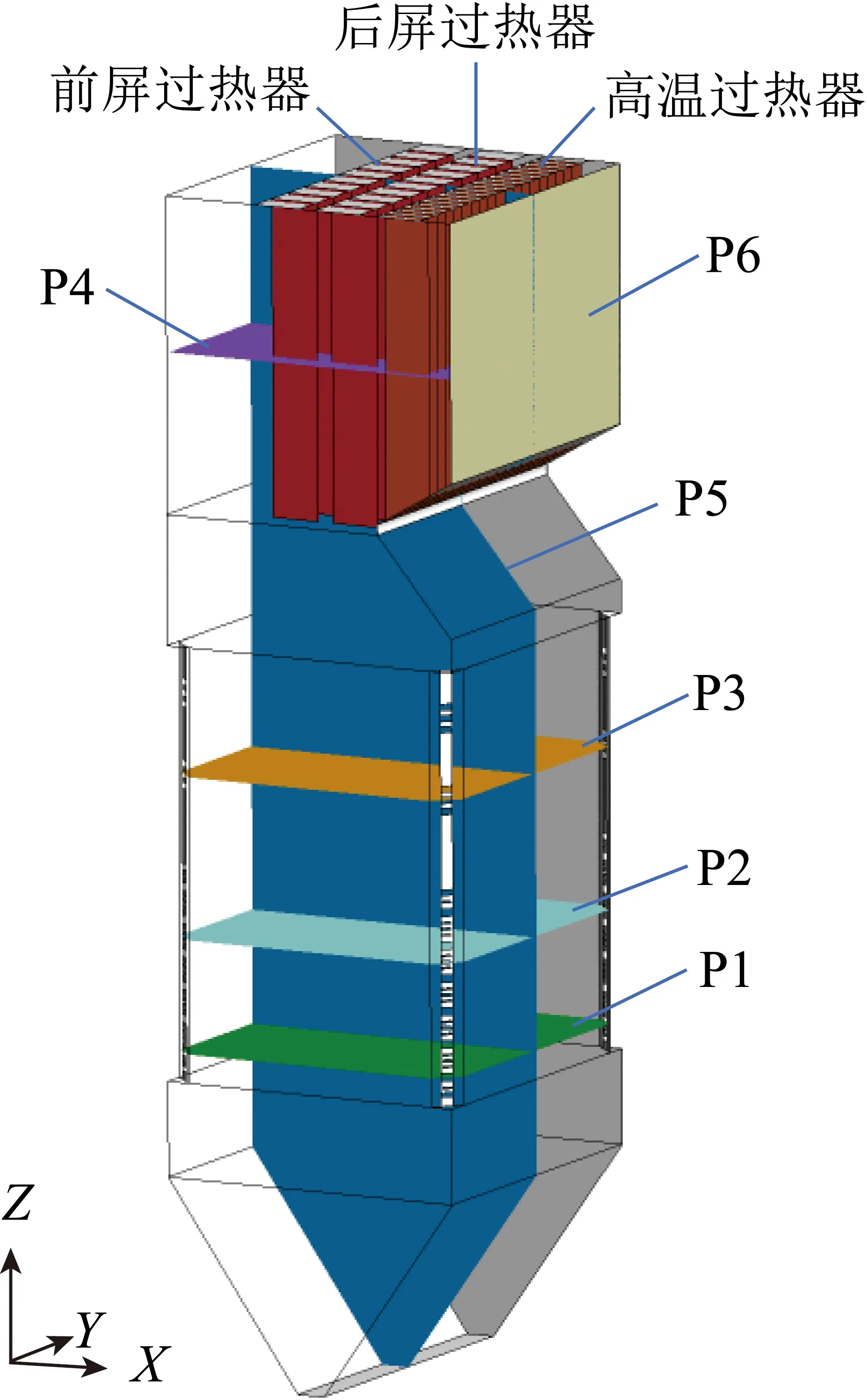
图1 锅炉模型三维结构

燃烧器布置在炉膛四角，如图2所示。在水平截面上，一次风沿逆时针方向与燃烧器水平截面中心线夹角3°进入锅炉炉膛；二次风进风也为逆时针方向，与一次风进风方向夹角为α，对一次风进行启动旋转；燃尽风进入炉膛方向与一次风方向夹角为β。在燃烧器竖直截面上，燃烧器底部为托底二次风AA，所在高度为16.03 m；由下到上依次布置为A、B、C、D、E、F等6层一次风，最下层一次风距离最上层一次风10.26 m；每层一次风之间布置1组二次风，每组二次风分为上、下偏转二次风以及中间的直吹二次风；在燃烧器上方位置布置2组燃尽风喷口，下部1组为3层低位燃尽风，上部1组为3层高位燃尽风，2组燃尽风之间高度为4.5 m。

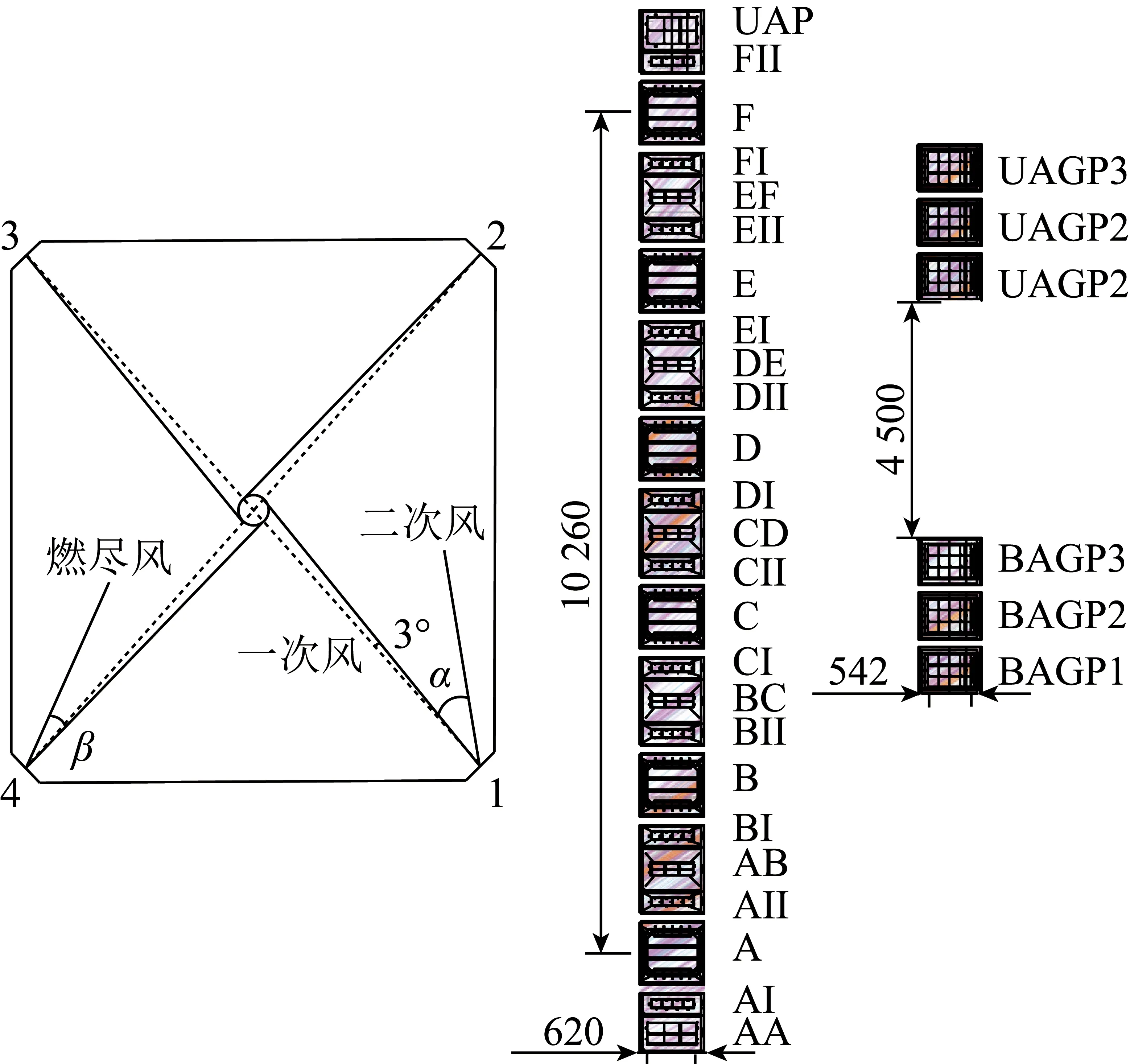
图2 燃烧器布置

2 模拟计算方法

2.1 模型网格的划分

数值模拟中锅炉模型的网格划分状况如图3所示，锅炉模型网格的划分主要采用分区域划分的策略，除冷灰斗区域为四面体网格外，其余部分均采用六面体网格，以提高计算效率及精度，为了防止在燃烧器区域由于气流的湍流强度较大导致可能出现伪扩散现象，因此主要对该部位网格进行加密处理，加密的网格数量分为3种。

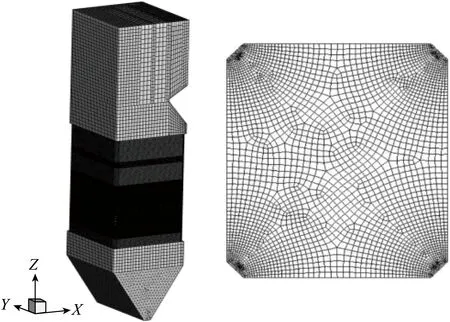
图3 锅炉网格划分

网格无关性验证如图4所示，对1 020 000、1 520 000、2 020 000个3种不同数量网格模型进行无关性验证。3种数量网格在数值模拟时，炉内20～50 m高度处温度有所差别，其中网格数量为1 020 000 个的工况温度与2 020 000个的网格差别较大，最大误差为64.6 K；网格数量为1 520 000与2 020 000个，虽然数量相差较大，但炉内温度分布较接近，最大误差为15.6 K。分析说明1 520 000个以上的网格均能满足数值模拟准确性的要求，为最大程度保证数值模拟计算的精度，最终确定数值模拟计算的网格数量为2 020 000个。

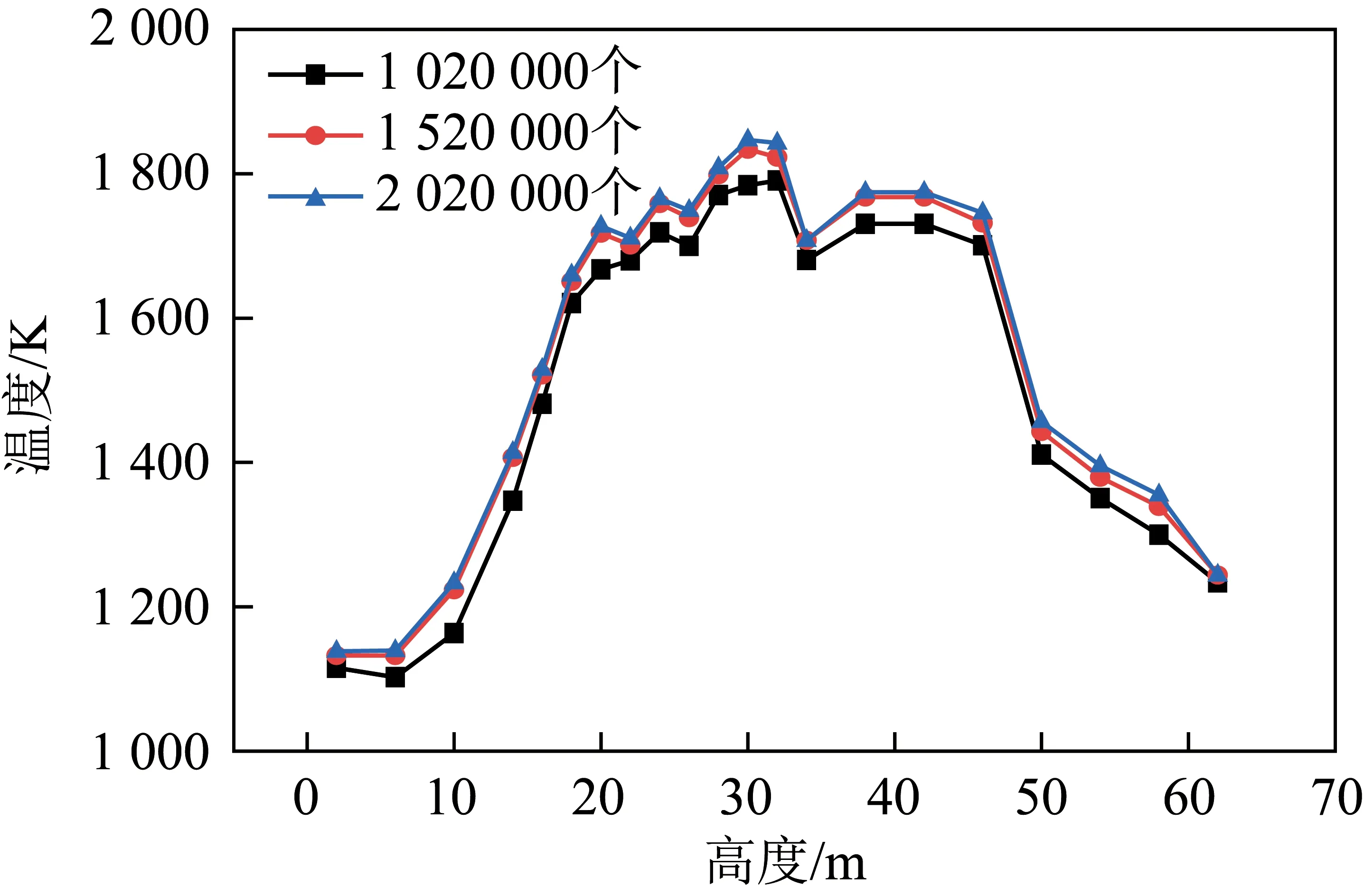
图4 网格无关性验证

2.2 数学模型

选取非预混燃烧PDF模型模拟炉内燃烧；选取Realizablek-ε模型修正炉内存在的旋转气流；选取P1辐射模型描述炉膛内部存在的气体与固体颗粒之间的两相辐射换热；选取Rosin-Rammler分布描述炉内固体颗粒的粒径分布状况；采用双方程竞争模型描述炉内煤粉颗粒的热解过程；采用动力学扩散控制模型描述炉内焦炭的燃烧过程；气相吸收系数采用WSGGM进行计算；同时采用SIMPLE算法；采用Green-Gauss Cell Based格式描述梯度离散项；采用PRESTO!格式描述压力离散项；其他离散项均采用二阶迎风格式。数值模拟计算时，先迭代得到稳定流场，然后进行热态计算。

2.3 边界条件

在设计工况下锅炉的煤耗量为219 t/h，锅炉总风量为1 926 t/h；数值模拟计算过程中，将燃烧器入口边界设置为速度入口边界，将锅炉炉膛出口边界设置为带有微负压的压力出口边界，炉膛壁面为无湍流流动、无滑移壁面，炉膛顶部的屏式过热器、高温过热器壁面设置为950、980 K的恒温壁面，煤粉颗粒的最小粒径为10 μm，最大粒径为250 μm，平均粒径为56 μm，炉膛内煤粉颗粒的分布指数为n=1.15。设计工况下具体燃用煤质参数见表1，一、二次风以及燃尽风等的风量状况见表2，数值模拟中进入炉膛的风量为总风量扣除漏风后的剩余部分。

表1 煤种工业分析和元素分析

表2 风速参数

2.4 工况设置

桃志鹏等[17,22-23]研究燃尽风反切角度、燃尽风偏置状况、燃烧器上摆角度对炉膛出口烟温偏差的影响，目前660 MW四角切圆锅炉缓解烟温偏差最佳燃尽风反切角在25°以内、最佳燃尽风偏置在1.30以内、最佳燃烧器上摆角度在11°以内。该正交试验的因素及水平设置状况见表3，因素A为燃尽风的反切角度、因素B为燃尽风的速度偏置、因素C为燃烧器的上摆角度、因素D为二次风的偏转角度(因素B为锅炉右侧的燃尽风风速与锅炉左侧的燃尽风风速之间的比值；因素C中燃烧器上摆指锅炉上所有一、二次风喷口均向上摆动，“+”表示燃烧器向上摆动；因素D中“-”表示二次风沿逆时针方向与一次风夹角)，每个因素设计2个水平。选用正交试验表L8(27)，正交试验工况设置见表4。

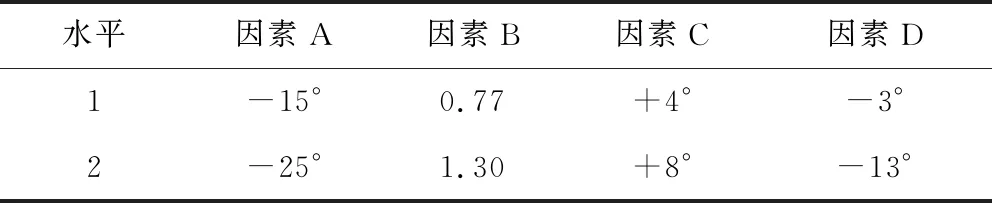
表3 数值模拟的因素和水平

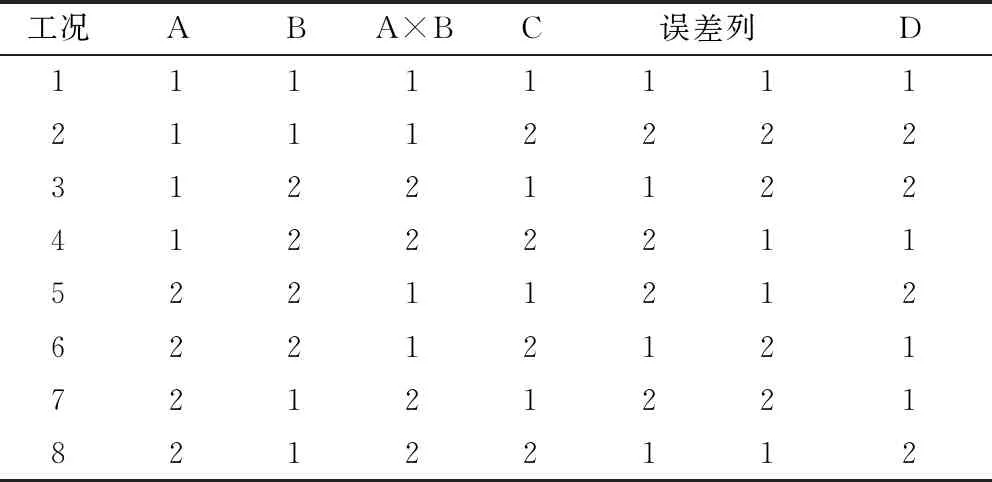
表4 工况设置

3 结果与讨论

3.1 模拟验证

为确保数值模拟的可靠性，将工况1高温过热器的数值模拟值与上海锅炉厂给出的锅炉设计值进行对比结果见表5。

由表5可知，高温过热器进出口部位的数值模拟值与锅炉厂的设计值之间的误差较小，试验证明数值模拟计算结果具有准确性。

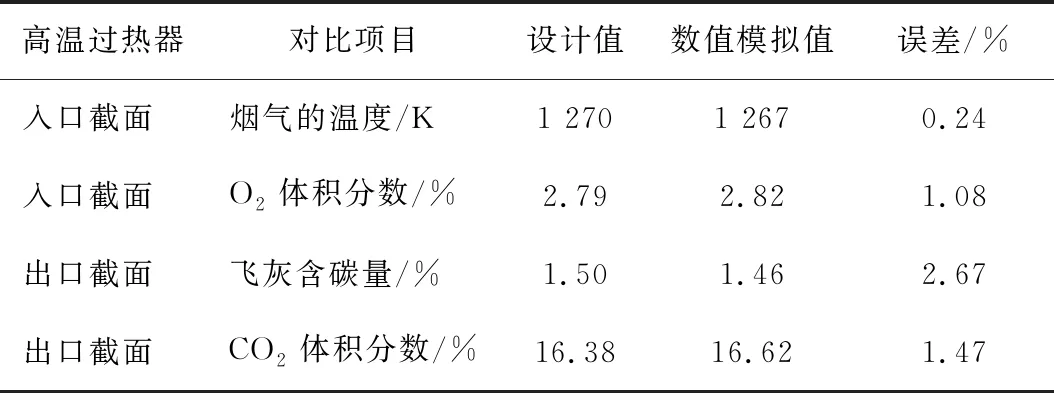
表5 高温过热器数值模拟值与锅炉设计值

3.2 炉内速度场分析

炉内各截面速度场分布状况如图5所示，各工况P1、P2截面上一、二次风上游气流冲击下游气流，形成良好切圆，由于燃烧器上摆角度以及二次风偏转角度的不同，切圆大小不同；在P3截面，随不同反切角度及风速的燃尽风加入，炉内切圆气流出现不同程度的偏斜；在P4截面，可看出各工况均存在一定程度的烟速偏差，工况1、4、6、7烟速偏差相对较低。

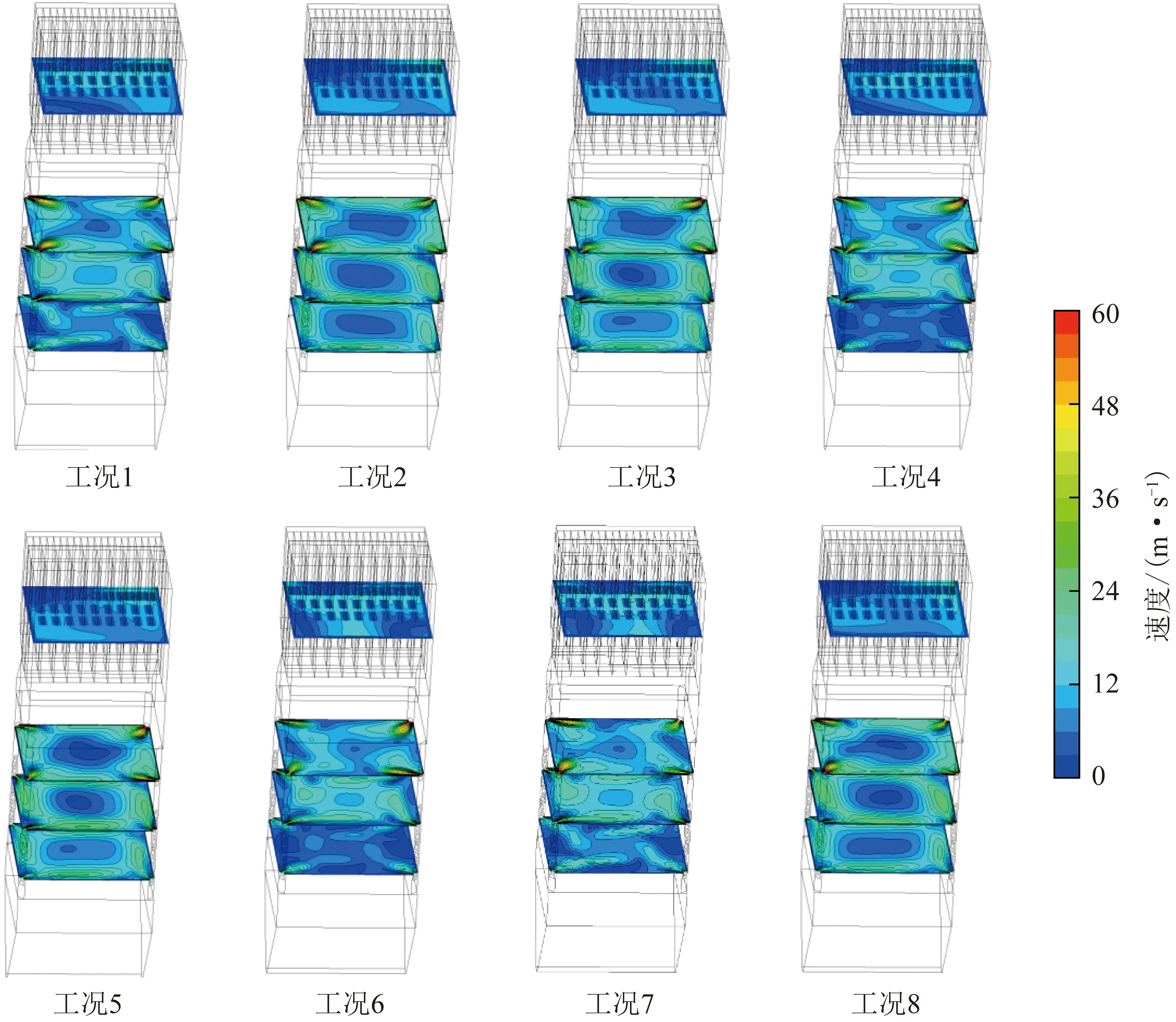
图5 炉膛内部的速度分布

3.3 炉内温度场分析

炉内P1、P5截面温度分布如图6所示，炉内最高温度可达2 000 K，满足燃烧设计需求，有利于煤粉燃烧及燃尽。P1截面各工况温度分布均呈四角切圆燃烧特征，截面高温区域主要集中在燃烧器喷口附近；随二次风偏转角度增大，造成切圆直径增大，截面中心位置温度降低，此时高温区域主要集中在炉膛壁面位置；P5截面各工况温度基本呈对称分布，高温区域主要在燃烧器附近及燃尽风上部区域，灰斗和上部水平烟道温度相对较低，并且燃烧器上摆角度增大，导致截面上高温区域上移。

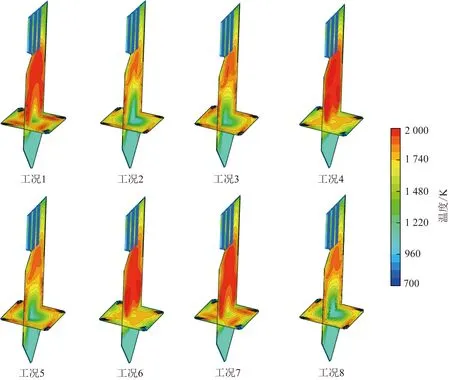
图6 炉膛内部的温度分布

3.4 P6截面速度及温度分布

P6截面速度分布如图7所示，各工况P6截面均有速度偏差。工况1高速区域集中在截面右上部；工况2、3、5、8高速区域主要集中在截面右上部，右下部也出现部分高速区；工况4、6、7截面高速区域分布相对较均匀。

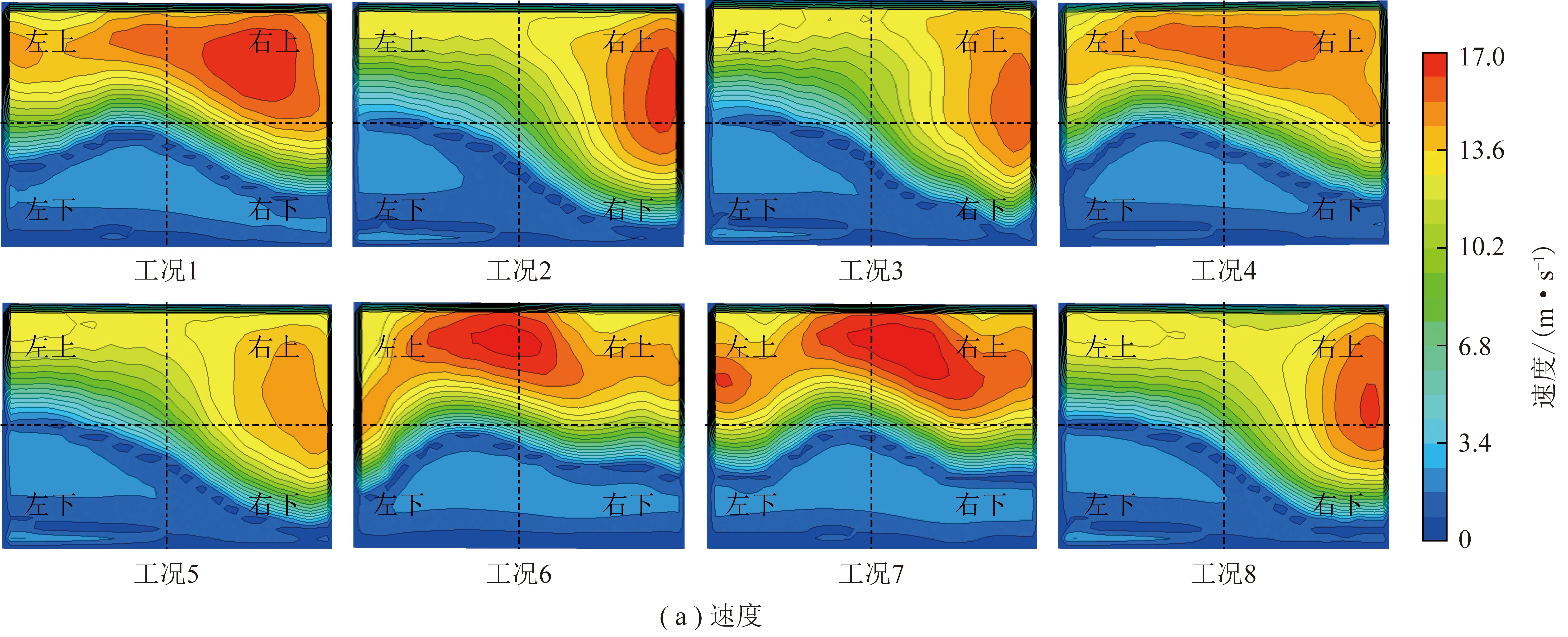
图7 炉膛出口截面上的速度以及温度分布

3.5 烟温偏差数值分析

引入温度偏差ΔT描述P6截面上右侧与左侧平均温度的差值;引入截面速度偏差因子Z以及截面温度偏差因子G，分别描述炉膛出口截面上左、右两侧速度比值及温度比值；引入截面的速度分布不均系数Mv以及截面的温度分布不均系数MT，分别用来描述炉膛出口截面上的速度分布以及温度分布的不均匀程度。具体定义如下：

(1)

(2)

(3)

(4)

(5)

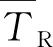
炉膛出口截面上的速度以及温度分布数值模拟结果代入以上公式进行计算，所得结果如图8所示，可知工况6的速度偏差因子及速度分布不均系数基本趋近于1，即P6截面速度偏差最小，速度分布最均匀；此时，温度偏差因子及温度分布不均系数也接近1，温度分布最均匀。

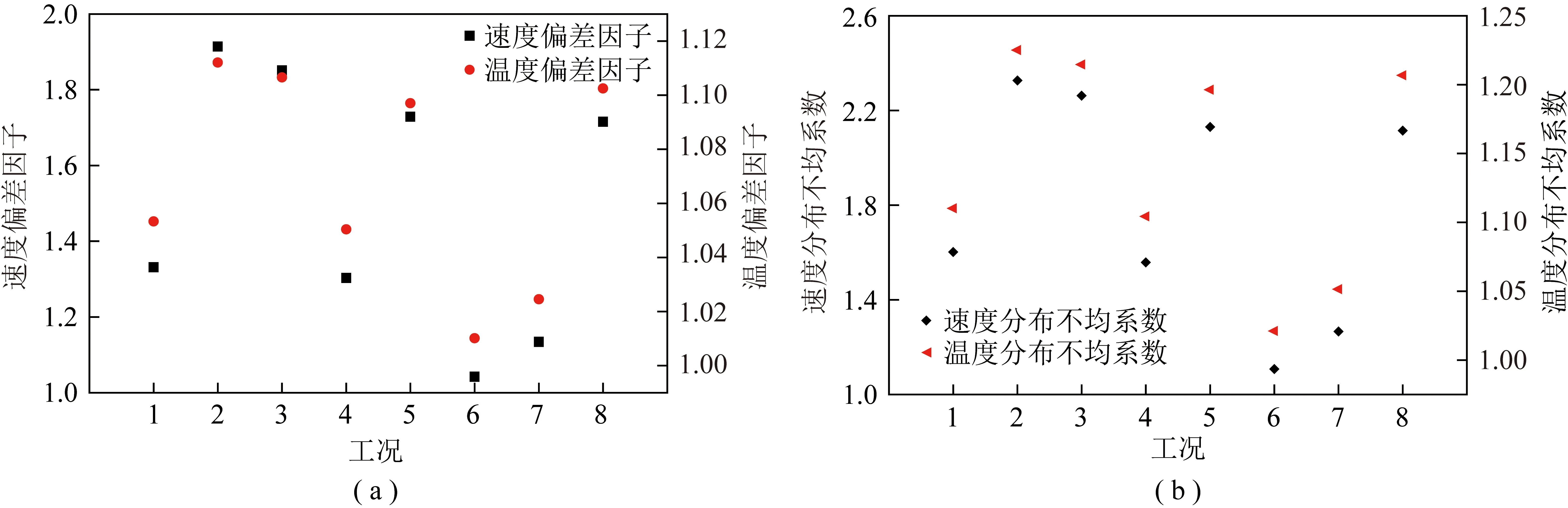
图8 P6截面速度及温度分布参数

3.6 极差及方差分析

(6)

(7)

(8)

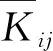
正交试验极差分析见表6，得出极差Rj大小顺序，R7>R1>R2>R3>R4，即因素主次顺序为D>A>B>A×B>C，其中D为首要因素。最佳的因素水平组合为A2B2C2D1，即工况6，此时P6截面烟温偏差为6.6 K。

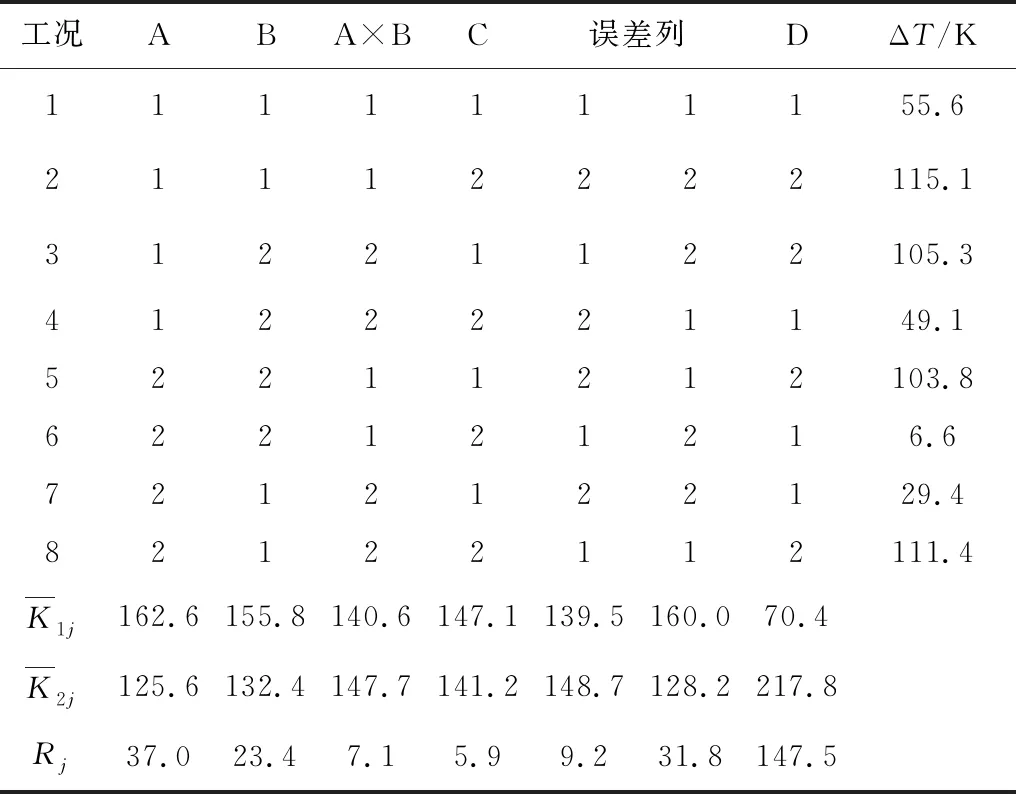
表6 正交试验极差分析

极差分析法无法提供因素对试验结果影响显著性的具体标准，因此引入正交试验方差分析法，方差分析结果见表7。

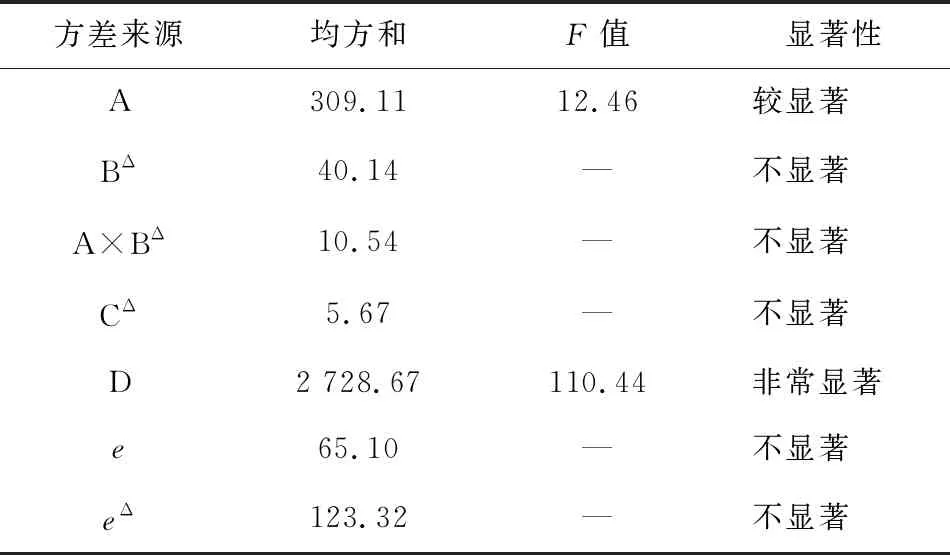
表7 正交试验方差分析

由表7可知，与正交试验极差分析法所得结果一致。正交试验方差分析得出：因素D对炉膛出口截面烟温偏差的影响非常显著，因素A对炉膛出口截面烟温偏差的影响较为显著，其余因素对炉膛出口截面烟温偏差的影响不显著。

3.7 权矩阵分析

利用以上极差及方差分析仅能得出因素水平对试验指标的重要性以及显著程度，为了分析各个因素的具体权重占比，进一步引入了权矩阵分析法。

根据正交试验表构建3层数据结构模型，即指标层、因素层、水平层，具体构建方法见表8。

表8 数据结构模型层次

通过3层数据结构，构建指标层矩阵M(14×7)、因素层矩阵T(7×7)、水平层矩阵S(7×1)，权重ω，具体定义如下：

ω=MTS。

(9)

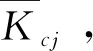
(10)

(11)

(12)

计算得出ω=(0.075，0.109，0.033，0.035，0.018，0.015，0.011，0.013，0.018，0.015，0.053，0.061，0.406，0.138)T，即各因素权重占比为：A为0.184，B为0.068，A×B为0.033，C为0.024，D为0.544，误差列权重为0.147；因素D权重最大，因素C权重最小；因素B、A×B、C所占权重小于误差列权重，说明这几个因素对于试验指标影响可忽略。此外，各因素在其水平上的最大权重为A2(0.109)、B2(0.035)、C2(0.013)、D1(0.406)，最佳组合为正交试验表中工况6。

4 结 论

1)二次风偏转角度增大导致炉内燃烧切圆直径变大；燃烧器上摆角度增大，会导致炉内高温区域上移。

2)通过极差及方差分析，对于正交试验指标炉膛出口截面烟温偏差，因素D(二次风偏转角度)为主要影响因素，影响高度显著；因素A(燃尽风反切角度)为次要影响因素，影响显著；其余因素无明显影响。

3)由权矩阵分析法，在因素层，因素D所占权重最大，因素C所占权重最小，依次顺序为：因素D(0.544)>因素A(0.184)>因素B(0.068)>因素A×B(0.033)>因素C(0.024)；在水平层，各因素不同权重排列为：水平A2(0.109)>水平A1(0.075)，水平B2(0.035)>水平B1(0.033)，水平C2(0.013)>水平C1(0.011)，水平D1(0.406)>水平D2(0.138)。

4)正交试验最佳因素水平组合为正交试验表中工况6，即A2(燃尽风反切角度25°)、B2(右侧燃尽风风速/左侧燃尽风风速=1.30)、C2(燃烧器上摆角度8°)、D1(二次风逆时针偏转3°)，该工况下，P6截面左、右两侧的温度偏差为6.6 K。