一种多稳态变势能函数压电俘能器及其特性研究
2022-07-27孙德华秦承武刘景阳
孙德华,谢 进,秦承武,杨 磊,刘景阳
(西南交通大学机械工程学院,四川成都 610031)
0 引言
由于传统的线性压电俘能器工作带宽非常窄,只有当外界激振频率与系统固有频率相近时才能有较好的俘能特性[1]。近年来,非线性压电俘能器因其具有更宽的工作带宽、发电效率更高而受到了广泛关注[2-3]。
研究表明:利用变势能函数结构能有效提高俘能器的性能。文献[4-5]提出了一种弹性支撑外部磁铁的结构,使系统在低幅激励下也能处于双稳振荡的状态;文献[6]在传统双稳态俘能器悬臂梁表面安装了带有弹簧的可移动磁铁,可移动磁铁与固定磁铁之间的磁力变化,则能够实现势能函数为可变,从而提高了俘能性能;文献[7]在传统悬臂梁俘能器的基础上,将固定端磁铁端增加了一个机械结构,以使势能函数发生变化;文献[8-9]提出了在具有末端磁铁的水平悬臂梁外垂直放置一个有末端磁铁的柔性竖直梁,通过柔性梁储存磁势能,从而实现变势能函数的俘能器结构;文献[10]在传统双稳态俘能器的外置磁铁上附加了一根弹簧,形成了一种新的变势能函数俘能器。
然而,目前大多数文献研究的变势能函数俘能器都只是双稳态的势能函数。近年来有学者提出的多稳态俘能器相较双稳态俘能器具有更低的势垒[11-12 ]。因而,在多稳态系统中再引入变势能函数的机制,则有望进一步提高俘能器的性能。
本文提出通过增加磁铁数量形成多稳态变势能函数的压电俘能器。研究了将增加磁铁安置在不同位置时,系统的势能函数及俘能器的动力学特性和俘能特性,说明了这种新型俘能器具有更加优越的性能。
1 多稳态变势能函数俘能器的结构及其数学模型
1.1 多稳态变势能函数俘能器的结构

图1 多稳态变势能函数俘能器的结构示意图
图1为多稳态变势能函数俘能器的结构示意图。长为LP的压电片粘附在长为L的悬臂梁表面,称此梁为压电梁。压电梁末端固定一块质量为mA的磁铁A;当系统静止时,质量为mB的磁铁B位于过磁铁A的垂线上,与磁铁A之间的距离用d0表示,磁铁B通过刚度为K的弹簧与基座相连。本文在此双稳态变势能函数俘能器的基础上,增设了固定磁铁C和D,与磁铁B水平距离分别用d1和d2表示,垂直方向的距离用c表示。z(t)为系统受到的外部激励的方向。
1.2 多稳态变势能函数俘能器的数学模型
本文中,用w(x,t)和u(x,t)表示梁在x处水平方向和竖直方向上的位移,s(t)表示磁铁B相对于基座水平方向上的位移。
采用扩展的哈密顿原理推导出压电系统的动力学方程。扩展哈密顿原理的计算表达式为
(1)
式中:q为压电梁的广义位移;s为磁铁B相对于基座产生沿x轴的位移;t为运动时间;V为压电片的电压;L为系统的拉格朗日函数;δW为非保守力所做虚功的变分。
系统的拉格朗日函数可表示为
L=T-U
(2)
式中:T为系统的动能;U为系统的势能。
系统的动能包括压电梁的动能、磁铁A的动能和磁铁B的动能,即
(3)
式中:m为悬臂梁单位长度的等效质量;mA和mB分别为磁铁A和磁铁B的质量。
系统的势能包括梁的应变势能、弹簧的弹性势能、压电片电势能和磁铁间的磁势能,即
(4)
式中:EI为梁的抗弯刚度;K为弹簧的刚度;θ为机电耦合系数;CP为等效电容;Um为磁铁间的磁势能。
根据磁偶极子模型,多稳态变势能函数系统的磁势能为
Um=UmB+UmC+UmD
(5)
式中:UmB、UmC、UmD分别为磁铁A和磁铁B、C、D之间的磁势能,计算公式分别为:
(6)
(7)
(8)
式中:μ0为真空磁导率;mA、mB、mC、mD分别为磁铁A、B、C、D的磁偶极矩;rAB、rAC、rAD分别为磁块A到磁铁B、C、D的方向矢量。
非保守力所做的虚功δW由机械阻尼和电荷输出组成,可表示为
(9)
式中:c1和c2分别为梁和弹簧的黏性阻尼;Q为流经负载R的总电荷。
为了得到系统的离散模型,本文采用了Galekin法[13]对拉格朗日函数进行离散。假设梁在运动过程中,梁的一阶振型起主导作用,压电梁的纵向位移w(x,t)可表示为
w(x,t)=φ(x)q(t)
(10)
式中:φ(x)和q(t)分别为压电梁的一阶振型函数和压电梁的广义模态坐标。
根据梁的边界条件,振型函数可以表示为
φ(x)=1-cos(2πx/l)/2
(11)
将式(2)、式(3)、式(4)、式(9)带入式(1)中,可得到系统的动力学方程为
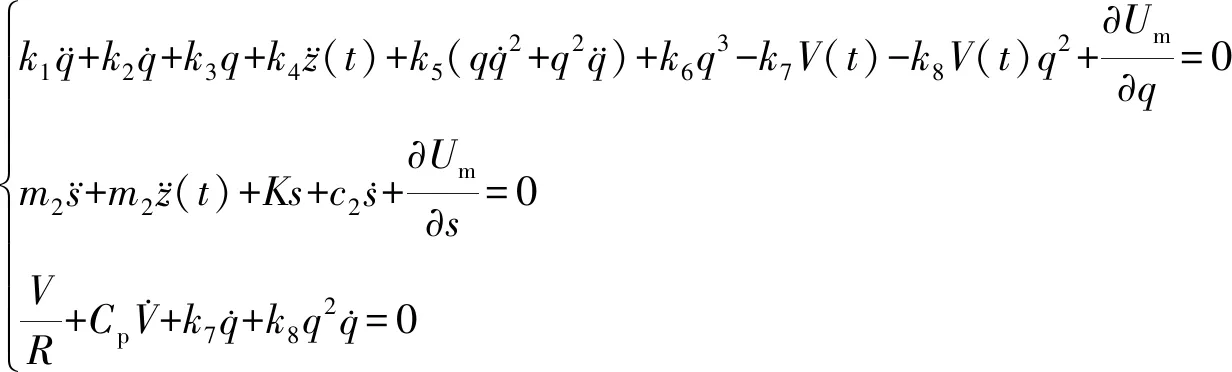
(12)
式中:k1为压电梁的等效质量;k2为等效阻尼系数;k3、k6分别为等效线性刚度和等效非线性刚度;k5为梁的非线性耦合项;k7、k8为梁的等效机电耦合系数。
本文研究的外激励为简谐激励,激励的表达式为
(13)式中:A为激励幅值;ωe为激励频率。
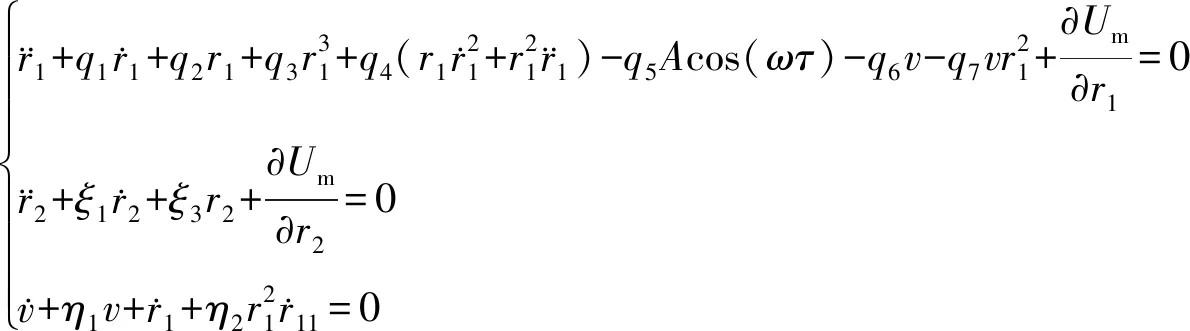
(14)
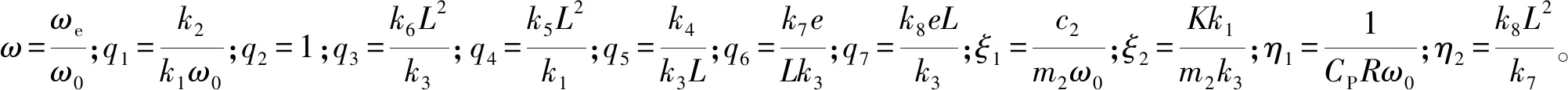
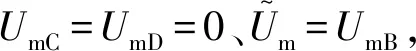
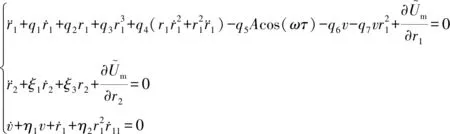
(15)
2 多稳态变势能函数俘能器的势能函数及其变化规律
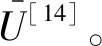
由式(5)和式(12)可得本文提出的多稳态变势能函数俘能器的势能函数表达式为
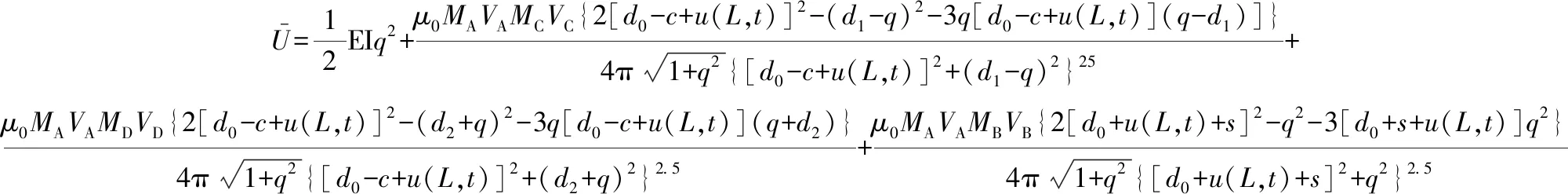
(16)
由式(16)可以看出系统的势能函数与初始磁铁间距d0、磁铁B的位移s、压电梁的位移q、磁铁C和D与磁铁B水平方向上的距离d1和d2等参数有关。实际上,俘能器非线性磁力的变化是势能函数变化的主要原因。在俘能器工作时,磁铁B的位移s、梁的位移q随着系统运动而发生变化,导致磁力的大小发生变化,从而会使系统势能函数曲线发生变化;而磁铁C和磁铁D的增设,使得系统稳定平衡点的数目发生变化,即系统稳态数目发生变化。
图2为初始磁铁间距d0=30 mm,磁铁C和磁铁D关于磁铁B对称,d1=d2=18 mm,系统的势能函数随磁铁B的位移s及压电梁的位移q的变化曲面。
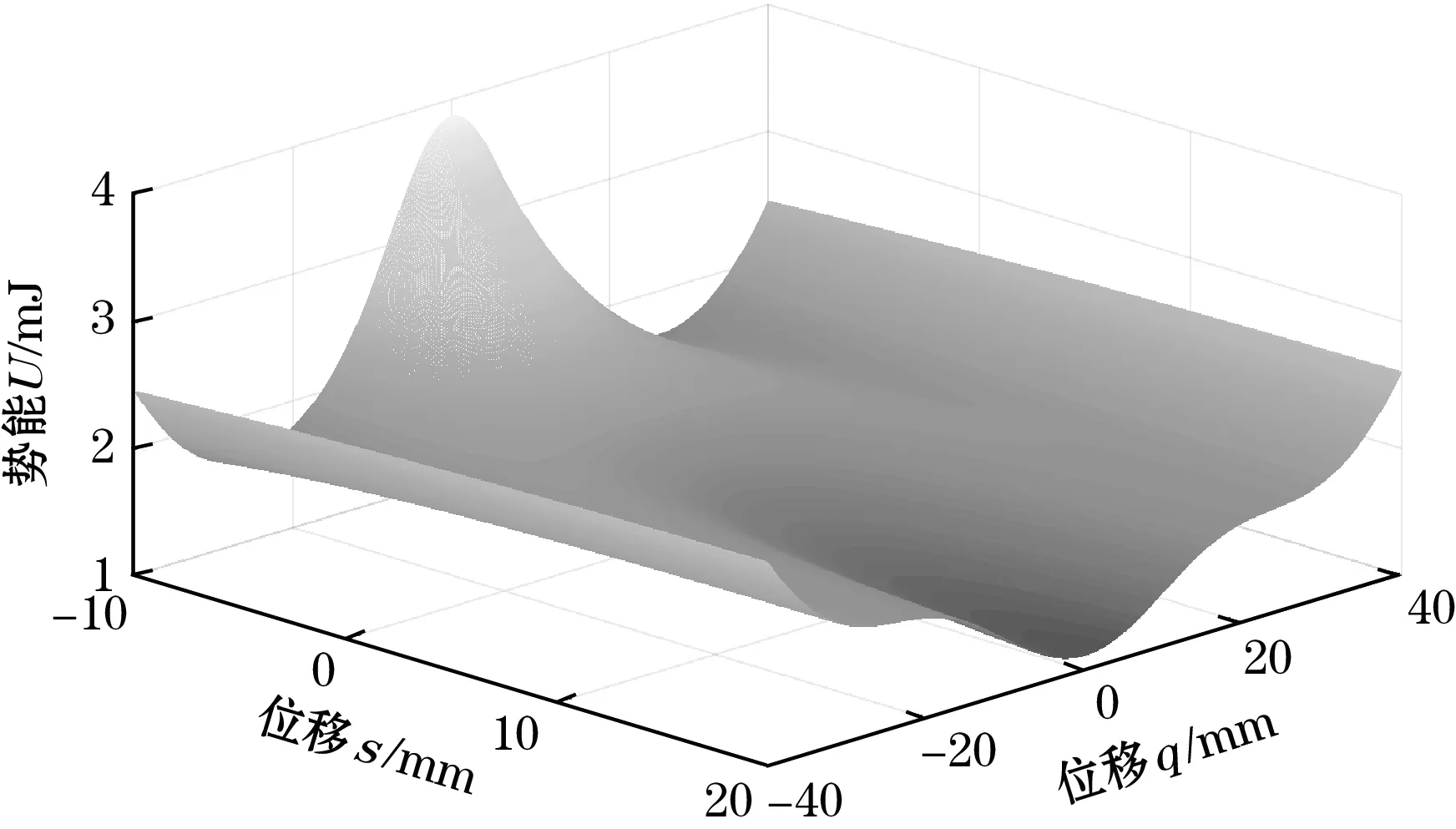
图2 系统势能函数的变化规律
从图2可以看出:在磁铁B的位移s从-10 mm增大到+20 mm的变化过程中,系统的势能函数由具有2个势阱的双稳态变为了具有3个势阱的三稳态,再变为一个势阱的单稳态;同时,势垒逐渐降低。
为了更加清楚地展示系统稳定点的变化,以磁铁B的位移s为参数,作出压电梁的平衡点q0的分岔图,如图3所示。
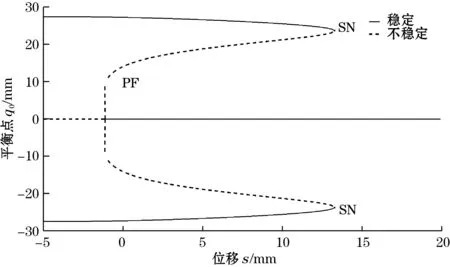
图3 压电梁平衡点关于磁铁B的位移s的分岔图
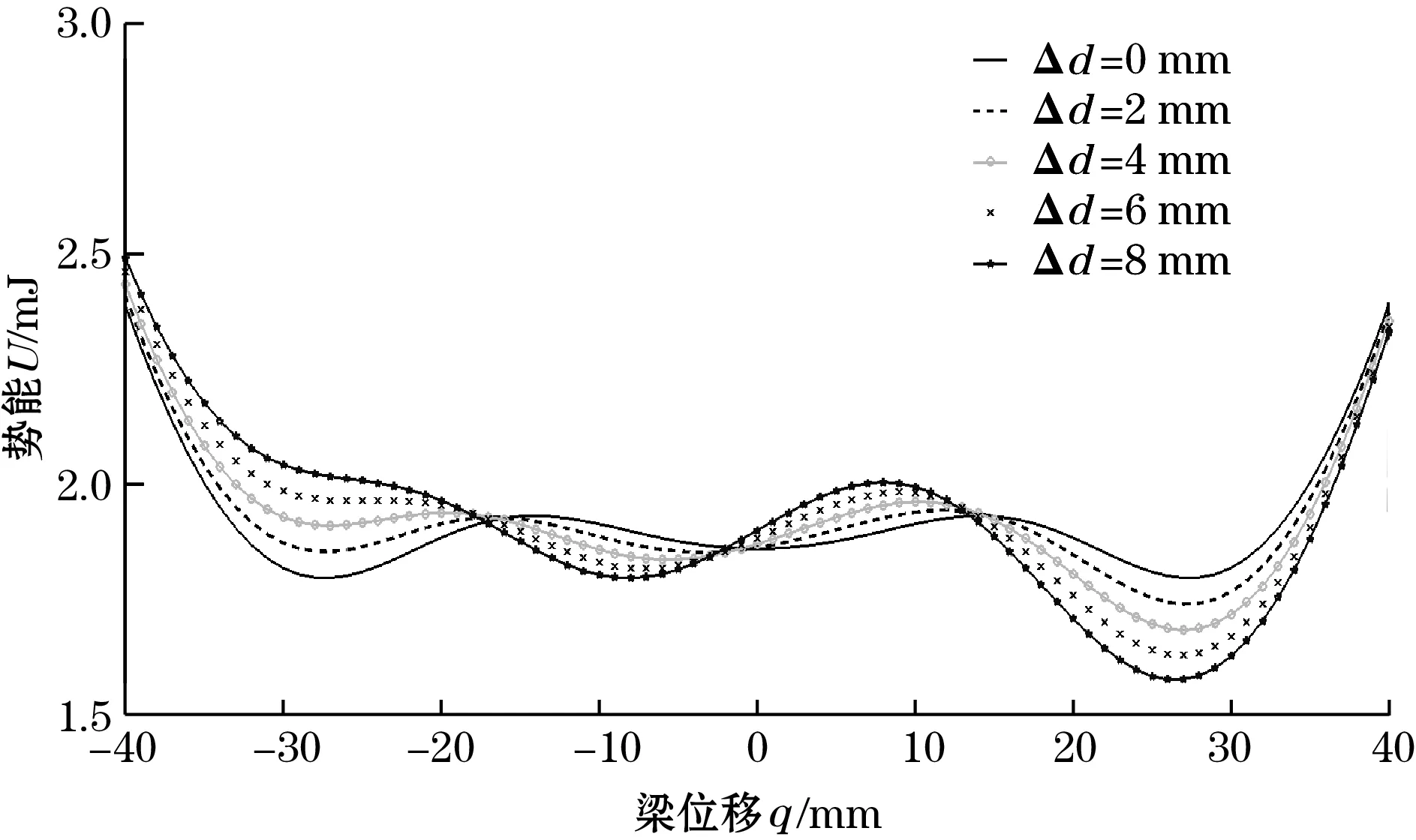
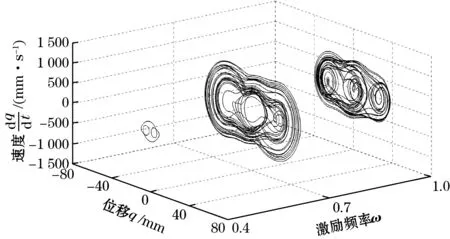
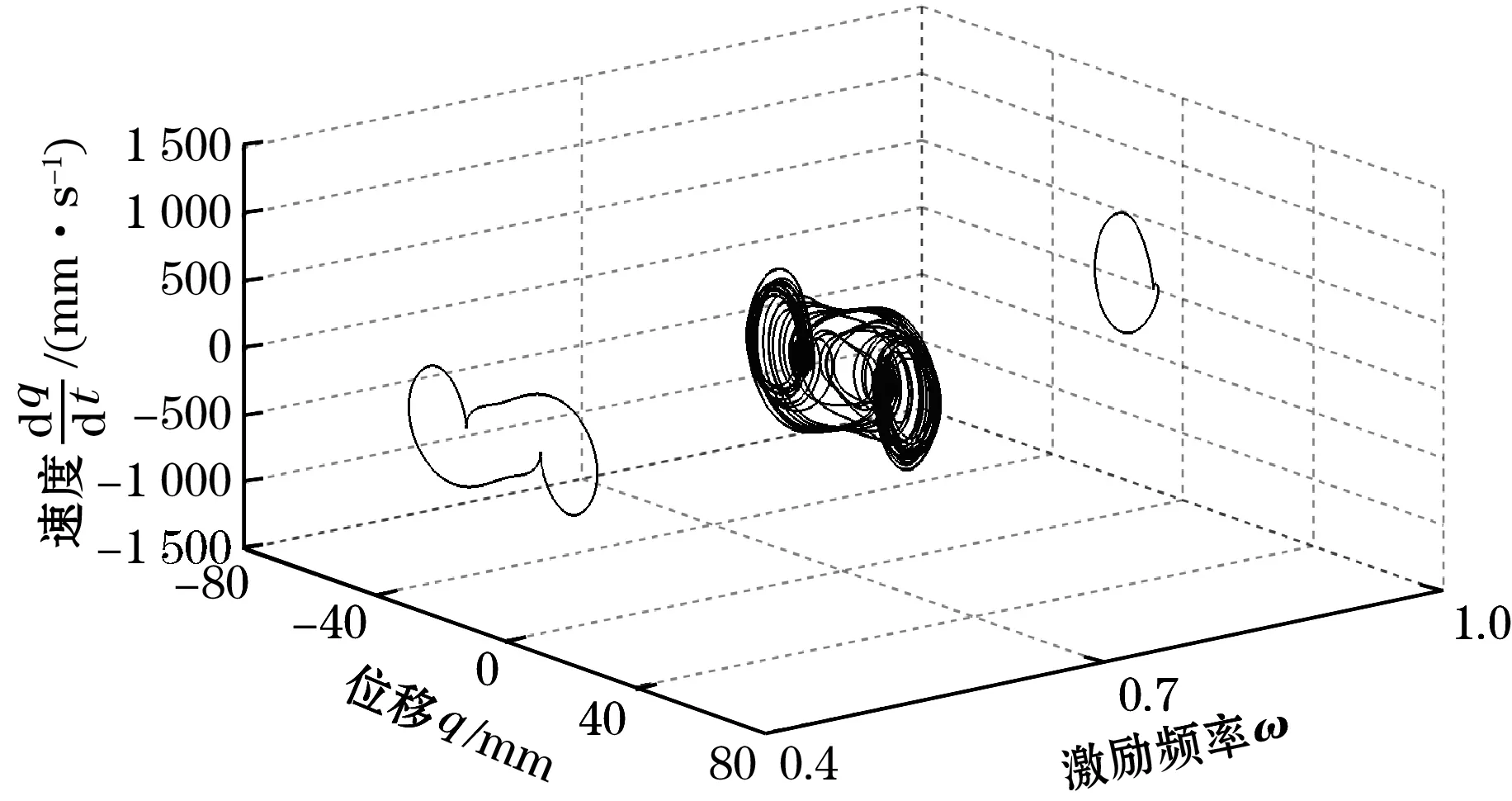
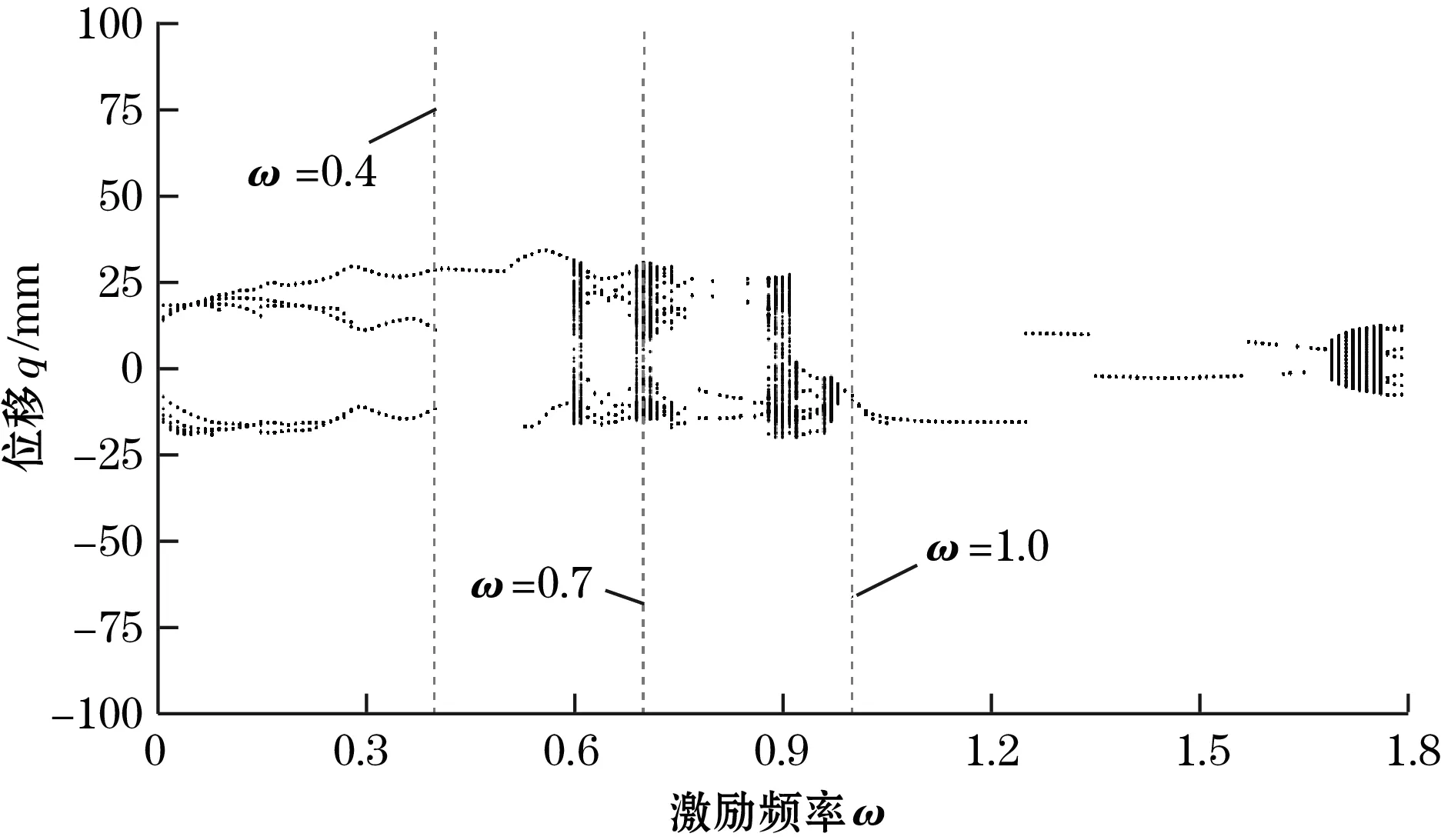
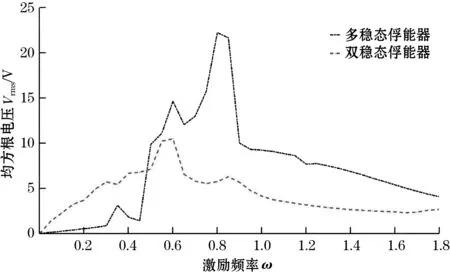
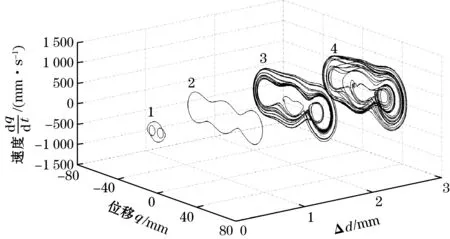
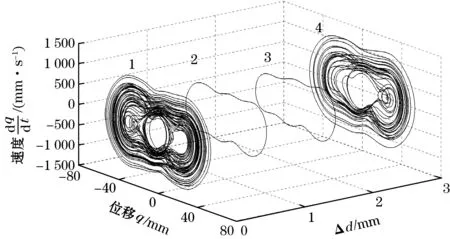
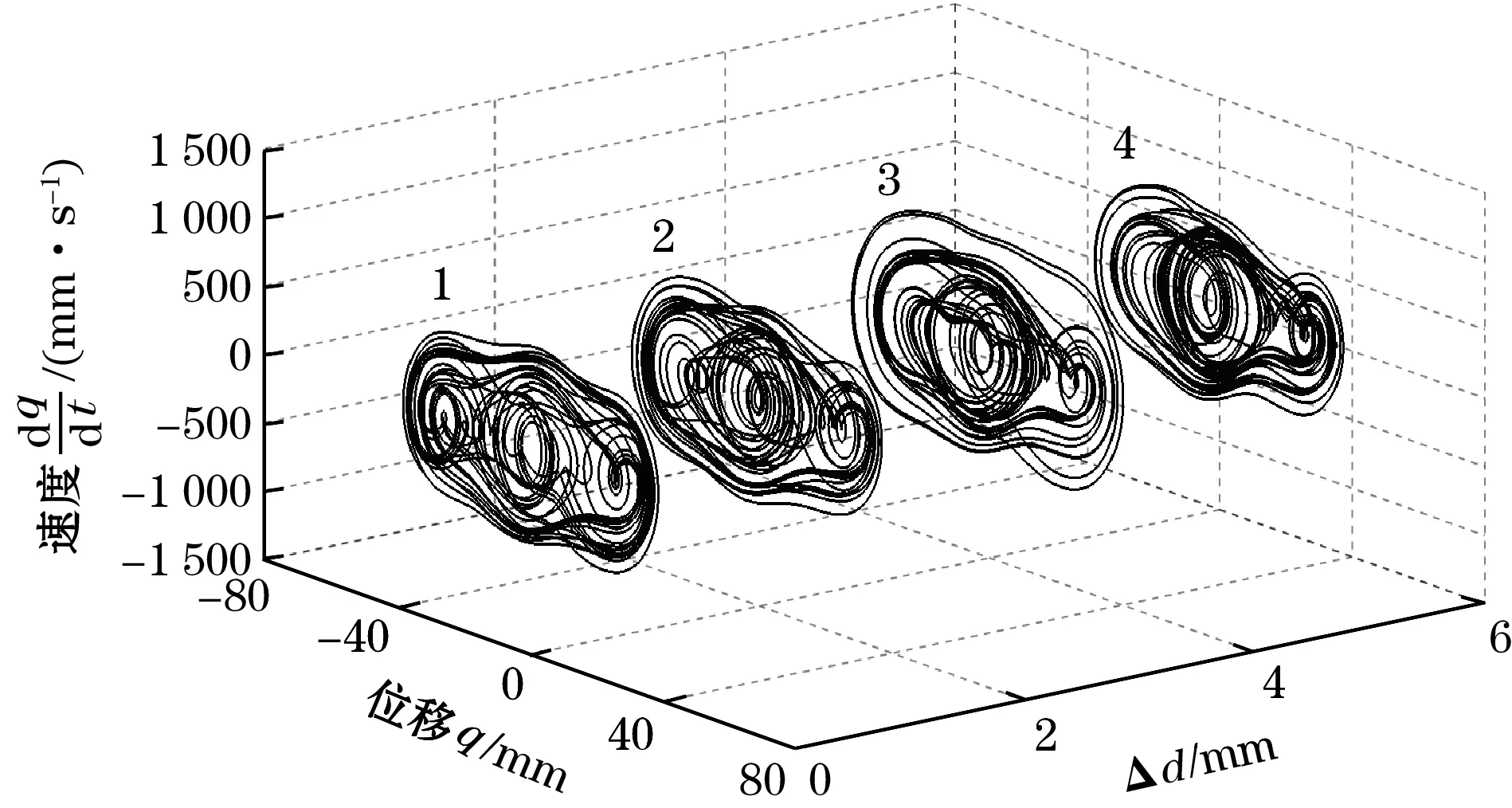
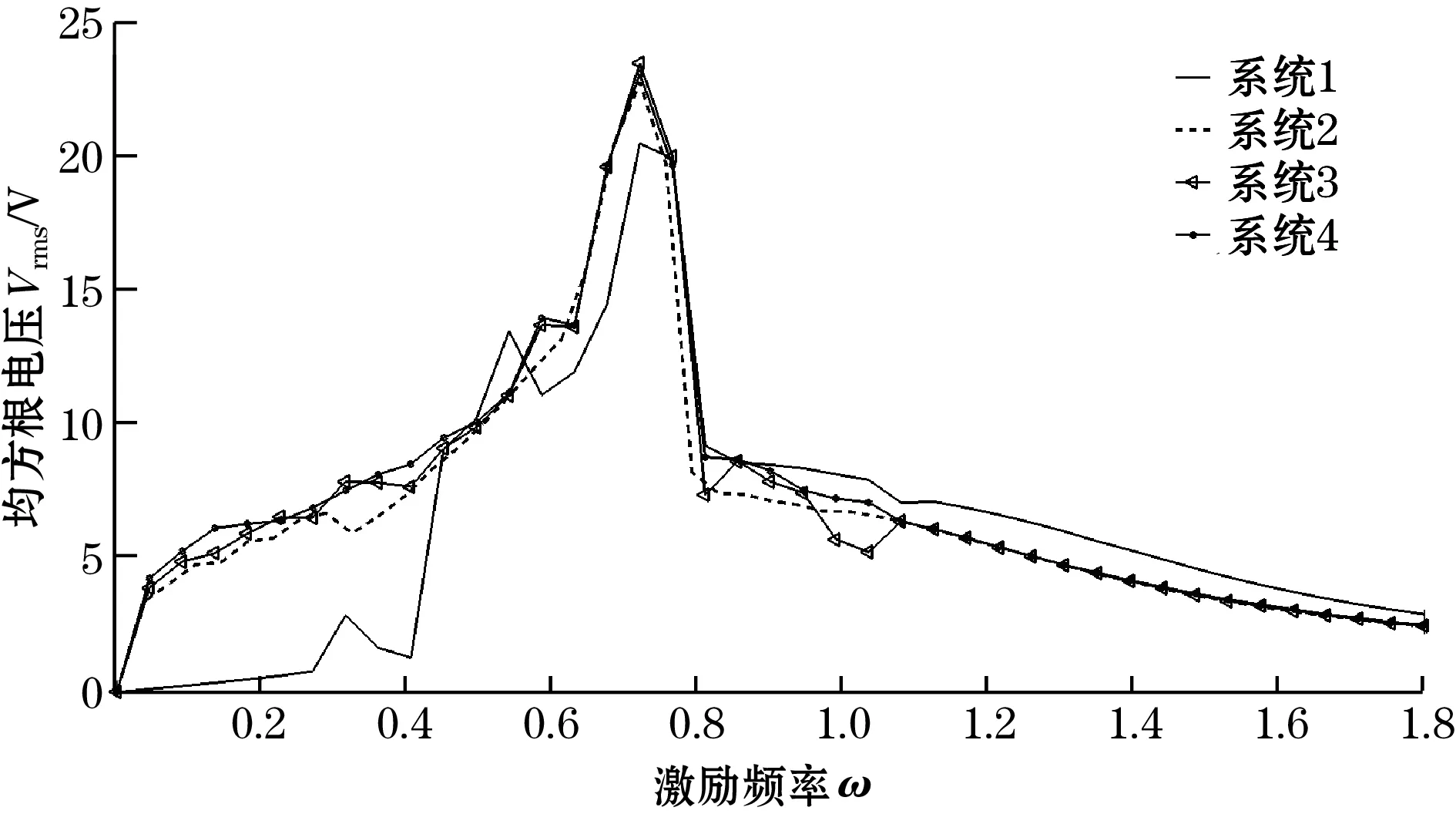
从图3可以看出:系统在s=13.3 mm处有2个对称的鞍节分岔SN,在s=-1.1 mm处有一个叉形分岔PF。由此可知:当-5 mm 如果磁铁C和磁铁D关于磁铁B的位置不对称,那么,压电梁末端受到非对称的磁力,势能函数也会呈现出非对称的状态[15-17]。以Δd=d1-d2表示磁铁C和磁铁D关于磁铁B的对称位置关系。若d1+d2保持不变,则意味着磁铁C和磁铁D同步地向左或向右移动。在这一条件下,可称为磁铁C和磁铁D的偏置量。 现以d1+d2=36 mm为例,分析磁铁B的位移s=0时,磁铁C和磁铁D的偏置量Δd对压电梁平衡点的影响。图4为压电梁的平衡点q0关于Δd的分岔图。图中Δd>0,表明磁铁C和磁铁D同步地向右移动。 图4 压电梁平衡点关于的分岔图(s=0) 由图4可知:当0 mm<Δd<3.11 mm时,系统有3个稳定的平衡点和2个不稳定的平衡点,系统仍然是三稳态状态,但是,与图3相比较,2个不稳定平衡点和中间稳定平衡点位置均发生了变化,而上下两侧所对应的另外2个稳定平衡点的位置基本上未发生变化;当Δd>3.11 mm时,系统有2个稳定的平衡点和1个不稳定的平衡点,系统变为双稳态状态。 图5为s=0时,势能函数随磁铁C和磁铁D的偏置量Δd的变化规律。 图5 Δd取不同值时系统势能函数的变化规律(s=0) 由图5可以直观地看出:当Δd=0时,势能函数曲线为关于q=0的对称曲线;当Δd>0时,系统势能函数曲线关于q=0不再对称,随着Δd的增加,左侧势阱的阱深变小,右侧势阱的阱深变大。当Δd=4 mm时,系统左侧的势阱消失,系统将呈现为不对称的双稳态,同时,势阱与势垒的位置发生了明显的变化。 根据上述分析,可以将Δd=0的俘能器称为多稳态对称变势能函数压电俘能器,Δd≠0的俘能器称为多稳态非对称变势能函数压电俘能器。 本节重点讨论增加磁铁C和磁铁D前的双稳态变势能函数俘能器以及增加磁铁C和磁铁D后的多稳态变势能函数俘能器的动力学特性和俘能特性。 取d0=30 mm,d1=d2=18 mm,c=2 mm,外激励幅值A=6 m/s2,无量纲激励频率ω分别为0.4、0.7、1.0,始值取为[0,0,0,0,0]。在本文后续的研究中,若未作特别的说明,则均取与此相同的参数。 图6分别为多稳态对称变势能函数俘能器和双稳态变势能函数俘能器在不同激励频率时的相图。 (a)多稳态对称变势能函数系统 (b)双稳态变势能函数系统图6 激励频率ω取不同值时的系统相图 对比图6(a)和图6(b)可以看出:在低频率ω=0.4时,多稳态变势能函数俘能器在中间势阱处做小幅阱内运动,而双稳态俘能器则处于大幅周期运动状态;当ω=0.7时,2种俘能器均处于混沌运动状态,但多稳态变势能函数俘能器的振子的振动运动幅度明显大于双稳态俘能器;当ω=1,多稳态变势能函数俘能器处于混沌运动状态,而双稳态俘能器作阱内运动。 图7为2个系统关于激励频率ω的分岔图。由图7可知:当ω<0.5时,多稳态对称变势能函数系统处于阱内小幅运动状态,其位移响应小于双稳态变势能函数系统;当ω增大到0.5附近时,多稳态对称变势能函数系统出现了阱间大幅周期运动,其位移响应大于双稳态变势能函数系统;当ω在区间[0.65 1.2]范围内时,多稳态对称变势能函数系统处于阱间混沌运动状态,其位移响应明显大于双稳态变势能函数系统;当ω>1.2时,多稳态对称变势能函数系统处于阱内周期运动状态,位移响应减小。 旅游危机事件网络舆情系统包含多个要素及相互关系,其中,以舆情主体、舆情客体、舆情本体之间基于传播媒介而产生的互动关系最为显著,是推动旅游危机事件网络舆情系统运行的基本关系。旅游危机事件网络舆情系统的主客关系子系统是其最核心的组成部分。除主客关系之外,旅游危机事件网络舆情系统内部还包含有外围的组成部分,以及一些次要的系统关系,如图2。旅游危机事件网络舆情系统的主客系统和外围互动将其内部关系结构划分为主要关系和次要关系。 (a)多稳态对称变势能函数系统 (b)双稳态变势能函数系统图7 系统关于激励频率的分岔图 总而言之,磁铁C和D的增加有助于增强系统位移响应,并且使系统在更宽的激励频率范围实现混沌运动。 本文以均方根电压表示俘能器的俘能性能。双稳态变势能函数俘能器和多稳态变势能函数俘能器的均方根电压-激励频率响应曲线如图8所示。 图8 多稳态及双稳态变势能函数俘能器的频率响应曲线 从图8可知:当ω较低时,双稳态变势能函数系统有较大的输出电压。这是由于此时双稳态变势能函数系统能够越过势垒处于大幅周期运动状态,而多稳态变势能函数系统被困于中间势阱内作阱内小幅运动。当ω>0.5时,多稳态对称变势能函数系统的输出电压大于双稳态变势能函数系统,并且在ω=0.8附近出现较大峰值。这是由于当ω>0.5之后,多稳态对称变势能函数系统的位移响应明显高于双稳态变势能函数系统。 鉴于只有在低频很小的频率带宽内双稳态变势能函数系统的俘能性能略优于多稳态变势能函数系统,而在其他激励频率下多稳态变势能函数系统的俘能性能均优于双稳态变势能函数系统,因而可以说,多稳态变势能函数系统的俘能性能更高。 本节重点研究磁铁C和磁铁D的偏置量Δd对压电俘能器的动力学特性和俘能特性的影响。将Δd=0、1、2、3 mm所对应的系统分别简称为系统1、系统2、系统3和系统4。 图9为不同外激励频率下,系统1、系统2、系统3和系统4的相图。由图9(a)可知,当ω=0.4时,系统1被困于中间势阱内做小幅运动,其他系统均能越过势垒做大幅阱间运动;由图9(b)可知:当ω=0.7时,系统1和系统4处于混沌运动状态,系统2和系统3处于周期运动状态;由图9(c)可知:当ω=1时,4个系统均能够越过势垒作阱间运动,4个系统都处于混沌运动状态。 总之,磁铁C和磁铁D的偏置有利于压电梁实现阱间的大幅运动。 从以上分析可知:改变磁铁C和磁铁D的位置可以提高多稳态变势能函数系统在低频率激励下的俘能性能。 (a)ω=0.4 (b)ω=0.7 (c)ω=1.0图9 Δd取不同值时,系统的相图 图10 不同的多稳态变势能函数系统的频率响应曲线 本文提出了多稳态变势能函数压电俘能器。利用扩展的哈密顿原理推导了系统的动力学方程,分析了系统势能函数的变化规律,研究了简谐激励下系统的动力学特征和俘能特性。研究表明: (1)通过增加磁铁C和磁铁D,能使俘能器具有多稳态特性;运动磁铁B的位置s的变化,又使得势能函数曲线发生变化,从而形成了多稳态变势能函数的动力学系统。 (2)磁铁C和磁铁D关于磁铁B对称安装时,系统的势能函数曲线是对称的;磁铁C和磁铁D关于磁铁B不对称安装时,系统的势能函数曲线是非对称的。 (3)当外激励频率比较高时,对称的多稳态变势能函数俘能器能够产生出较通常的双稳态变势能函数压电俘能器更大的位移响应和均方根电压响应。 (4)多稳态非对称变势能函数俘能器在低频的外激励下也可实现大幅的阱间运动,输出较高的均方根电压。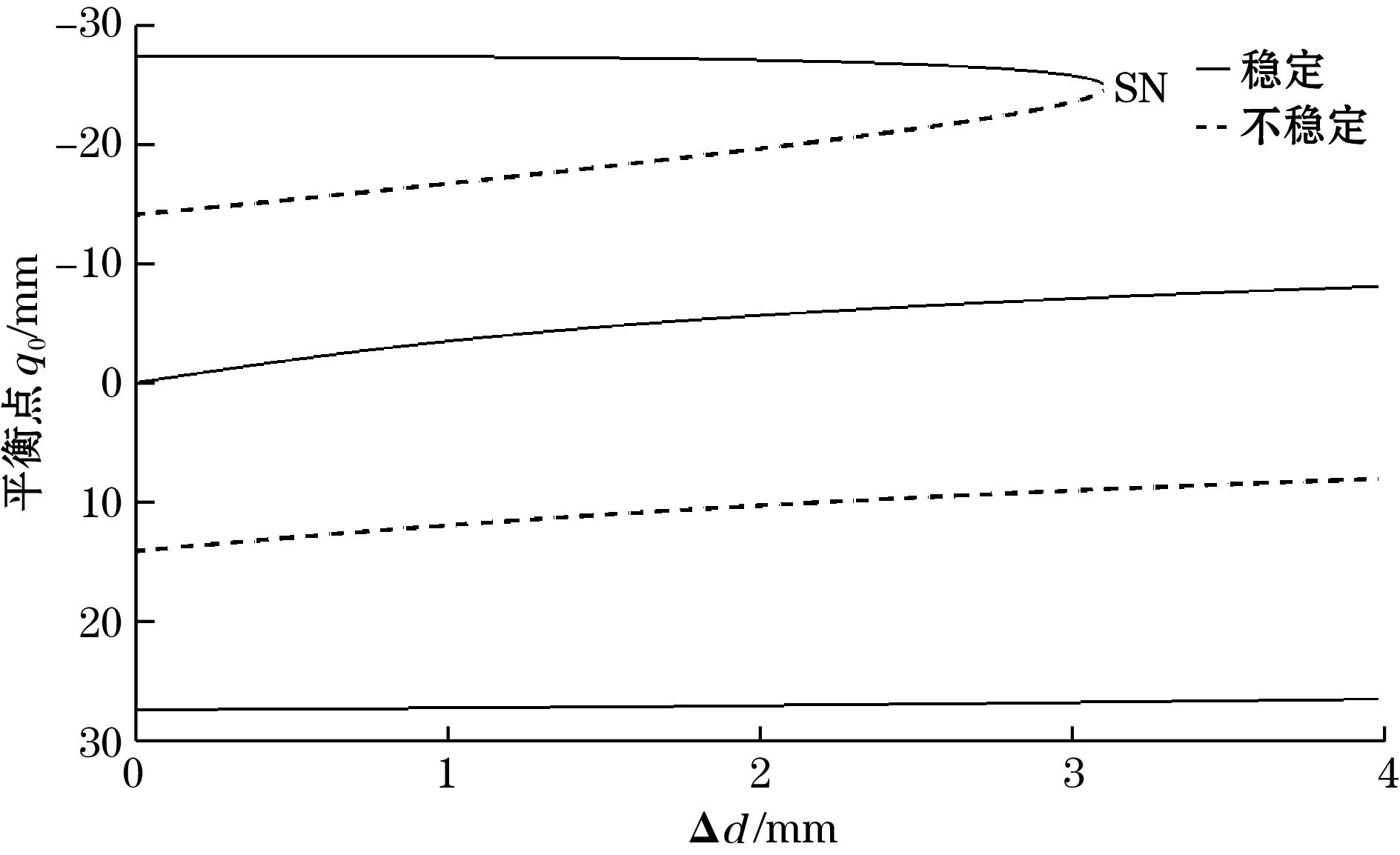
3 多稳态对称变势能函数压电俘能器的动力学特性和俘能特性
3.1 多稳态对称变势能函数压电俘能器的动力学特性

3.2 多稳态对称变势能函数压电俘能器的俘能特性
4 多稳态非对称变势能函数压电俘能器的动力学特性和俘能特性
4.1 多稳态非对称变势能函数压电俘能器的动力学特性
4.2 多稳态非对称变势能函数压电俘能器的俘能特性
5 结论
