等径气泡平行聚并行为对流场与传质过程的影响
2022-07-27陈光辉崔久军董纪鹏李建隆
陈光辉,崔久军,高 飞,董纪鹏,李建隆
(青岛科技大学 化工学院,山东 青岛266042)
在精馏、吸收、气液反应器等化工单元操作过程中,气泡的运动会改变气液相流动状态、接触面积等,进而对传质、反应等过程产生重大影响[1]。气泡聚并是指在气液两相流或多相流中,当两个以上气泡发生碰撞,合并成一个气泡的现象[2]。气泡频繁的聚并,使气液两相接触面积减小,从而对气液传质产生不利影响。由于气泡聚并过程的复杂性和短暂性,关于气泡聚并行为及对传质影响规律的研究一直是两相流研究的热点与难点。
目前主要采用数值计算与实验对气泡聚并行为进行研究[3-6]。陈阿强等[7]对气浮池内气泡聚并进行数值计算,考察了来液流量和回流流量对聚并过程的影响,发现回流流量较大时,气泡聚并频率提高;KEEP等[8]采用实验方法借助高速摄像技术考察了流变性质、表面张力对聚并的影响;SOUSA等[9]研究者利用PIV 技术观察了Taylor气泡在聚并过程的流场信息变化,认为非牛顿流体气泡相互作用距离大于牛顿流体。还有不少学者考察了表面活性剂、韦伯数以及温度、黏度等参数对聚并过程的影响[10-14]。气泡间距较小会提高聚并频率,对气泡聚并过程的临界距离及气泡间距对气泡聚并行为的影响规律缺乏研究。实际工业中气泡之间有垂直在线和平行在线等多种聚并方式,李少白等[15]采用数值模拟方法对垂直在线气泡聚并进行研究,证明了聚并行为受气泡间距和液相流变性质影响,但是对于平行聚并相关研究鲜有报道。
关于气泡聚并对传质的影响报道不多,ZUIDERWEG 等[16]分析了在精馏系统中表面现象对气泡聚并行为的影响,认为表面现象对传质的影响大于密度、扩散系数等其他物性的影响。沈鉴彪等[17]考察了相间传质诱导对聚并的影响,实验研究表明Marangoni效应使聚并时间随着温度升高呈先减小后增大的趋势。还有研究者试图对其进行定量分析,由于过程的复杂性未取得实质性进展[18-20]。
本研究采用数值模拟方法,在常温下80%CO2和20%N2混合气作为气相,以等径平行气泡作为研究对象,研究了气泡直径、气泡间距对聚并过程的影响并分析了聚并行为对相间传质的影响机理,以期更加深入的认识气泡聚并过程。
1 数学模拟模型及方法
1.1 控制方程
VOF模型对于气液两相流模拟具有独特的优势[21-23],本研究借助Fluent流场模拟软件,采用VOF模型开展伴随传质过程的气泡聚并过程的研究。

传质过程模型中假设气液相物性参数(比如密度、黏度等)为定值,与压力无关;气泡中只有CO2气体可以从气侧传质到液侧。对于传质过程的计算选用水溶液为液相,CO2和N2混合气作为气相。常温下CO2和N2在水中的溶解度分别为0.168 8 g·(100 g)-1、1.891×10-3g·(100 g)-1。
CO2气体从气泡内扩散到气液界面处,假设界面处平衡且穿过界面的CO2通量是连续的,即从气相传递到界面处CO2的量等于界面处传递到液相中的CO2的量。该组分在气液相中的质量守恒方程分别如式(4)、(5)所示:

其中,Y i,g是CO2在气相中的质量分数,D i,mg是CO2在N2中的扩散系数,为1.67×10-5m2·s-1,Y i,l是CO2在液相中的质量分数,D i,ml是CO2在水中的扩散系数,为1.96×10-9m2·s-1。
假设界面处符合亨利定律,CO2是连续穿过界面的,且界面处无传质累积量,可得到式(6):
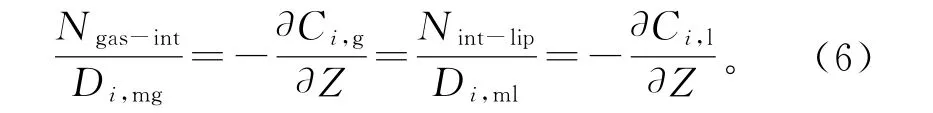
N为传质通量,下标gas、liq分别代表气相和液相,int代表气液界面。上述组分质量守恒方程通过开启组分运输方程实现,利用UDF(User Defined Function)功能进行计算机语言化实现传质过程。
1.2 网格划分及边界条件
几何模型及网格划分示意图见图1。二维矩形计算域选取尺寸为80 mm×80 mm,计算域尺寸大小可以忽略边壁对气泡的影响。为了提高网格的规整度,采用规整的四边形网格,以提高计算精度,减小计算量。本模拟中所有网格自动生成,数值计算前进行网格无关性检验,优化网格划分。
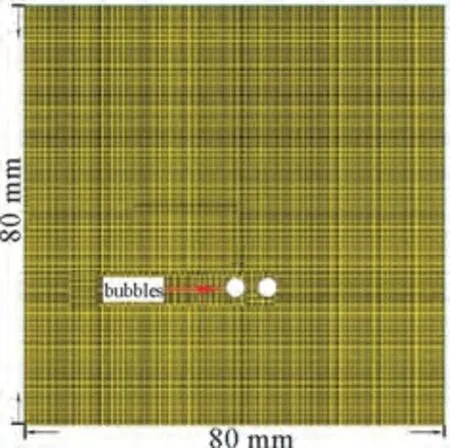
图1 几何模型及网格划分示意图Fig.1 Physical model and grid division diagram
计算域上边界设置为压力出口,其压力出口表压为0 Pa,其他为无滑移固体壁面。采用瞬态计算过程,时间步长为10-4s,压力-速度耦合方法采用SIMPLE法,压力的离散借助于PRESTO! 法,动量和体积分数分别采用QUIC 方法和Geo-Reconstruct方法。
2 结果与讨论
2.1 网格无关性
以直径4 mm 气泡为例,选取网格数为16 000、640 000和1 000 000这3种网格尺寸划分网格。以气泡在初始时刻的上升速度和CO2溶解量作为表征参数来验证网格无关性,结果见图2。当网格数达到64 000时,再提高网格精度对气泡上升速度和CO2溶解量影响不大,可认为在该网格数下网格精度够高,计算性价比良好,满足数值计算计算所需要求。
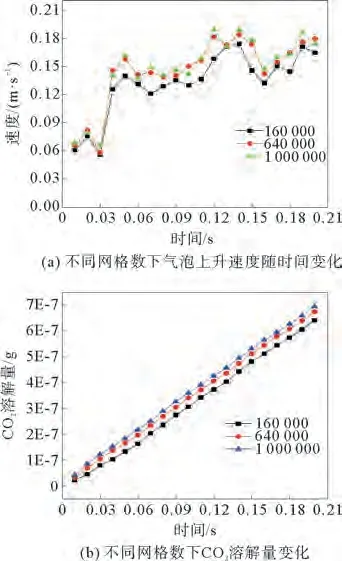
图2 网格无关性验证Fig.2 Grid independence verification
2.2 模型验证
采用上述传质模型对气泡进行模拟,并将计算结果与文献[25]中CO2传质实验结果进行对比,见图3。
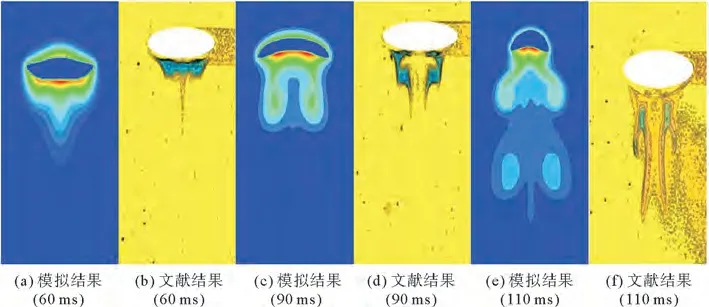
图3 模拟结果与文献[25]结果中CO2 浓度分布对比Fig.3 Comparison of the simulation results with the results in literature[25]
从图3看出传质过程主要发生在气泡正下方,随着时间的推移,在两侧移动形成对称的梯度浓度。气泡在不同时刻浓度分布与文献[25]实验结果吻合度较高。因此,采用的传质计算模型能够较准确反映气泡传质过程。
2.3 气泡直径对聚并过程中流场的影响
考察了初始直径为1~8 mm 的等径气泡,在间距为1 mm 时下气泡聚并过程中流线的变化规律。图4为初始直径分别2和6 mm 平行气泡聚并过程中流场分布变化规律。

图4 不同初始直径气泡聚并过程及流线分布Fig.4 Coalescence process and streamline distribution with different initial diameters
从图4可以看出,在初始时刻气泡在浮力作用下独立上升,气泡两侧均产生了对称的涡流。在涡流处流线分布密集、速度较快,气泡其它部位流线分布平缓,流速较慢。在上升过程中,气泡在向内旋转的涡流提供的作用力下,气泡向内运动,有相互靠近趋势。在气泡相互接触后形成了一个连接两个气泡的狭小通道,在通道上方产生了新的局部涡流。随着聚并过程的进行通道附近涡流消失,聚并后气泡周围流型与相同直径的单气泡流型接近。
对比初始直径2和6 mm 气泡聚并过程中流线分布规律看出,在气泡聚并初始阶段,不同初始直径气泡周围流场分布基本相似,气泡两侧涡流大小随气泡直径增大而增大。随着气泡上升,气泡接触后形成通道,通道上方涡流数量增多,气泡直径越大涡流数量越多,两侧的涡流结构越大,在聚并过程中气泡周围流线分布密集,液相运动更为复杂。初始直径为6 mm 气泡通道形成后,由于外侧涡流的影响较大,气泡受到向外的作用力,开始向外运动,通道液膜破裂,未实现气泡聚并。在聚并过程中产生的涡流结构,推动了气泡聚并,但是能够加速气液界面更新,一定程度上促进了相间传质进行。
图5为初始直径分别为2和6 mm 气泡平行聚并过程中压力分布变化规律。图5可以看出,在初始阶段气泡成椭圆形,气泡内部存在压力梯度,其中气泡顶部压力最高,为65 Pa左右;气泡间处于低压区,与气泡内形成较大的压力差,气泡向压力较低处运动,推动气泡相互靠近、接触,最后完成聚并。随着不断气泡上升,气泡受到的形体曳力不对称分布造成气泡形状发生变化,压力分布亦发生了改变。气泡两侧低压区随气泡直径增大而向下移动且范围减小;通道上方出现高压区,通道下方随气泡直径增大发生变化,由高压区变为低压区。聚并过程使泡内压力降低了30 Pa左右,直径为2 mm 气泡,气泡实现聚并,形状呈球帽形,压力分布与等径气泡相近;直径为6 mm 气泡压力差较小,气泡向两侧运动,未实现聚并。在涡流和压力差的双重作用下气泡从相互接触到液膜融合,最终实现聚并。
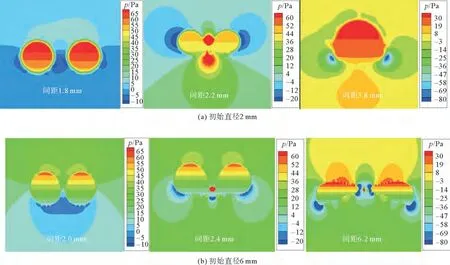
图5 不同直径气泡聚并过程的压力分布Fig.5 Pressure distribution in coalescence process with different diameters
图6给出了在气泡间距为1 mm 时不同物系中聚并距离随气泡直径变化关系。聚并距离是指气泡从开始到完成聚并气泡所上升的距离。从图6 看出,在相同黏度下,聚并距离随气泡直径的增大呈先减小后增大的趋势;气泡聚并距离随着物系黏度增大而增大,这是物种中黏度不同导致流动阻力增大造成的;当气泡间距为1 mm 时,初始直径大于6 mm气泡时,无法实现聚并。
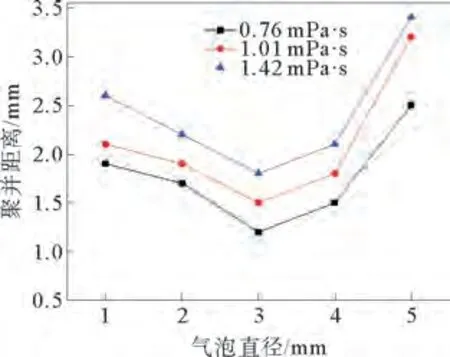
图6 聚并距离随气泡直径变化规律Fig.6 Variation of coalescence distance with bubble diameter
2.4 气泡间距对聚并过程中流场的影响
图7给出了等径气泡在不同间距时聚并过程中变化规律。从图7可以看出,气泡间涡流由于受到两侧气泡的挤压,涡流大小随着气泡间距的增大而增大;间距为1 mm 气泡接触后,在气泡间新增多个涡流结构,气泡间距越小新增涡流越大,其位置越高。这是由于气泡间距较小,气泡相互靠近挤压后涡流向气泡上方空间较大的地方发展。间距为2 mm 的气泡,在气泡两侧向外旋转涡流的作用力大于向内旋转涡流,气泡向外运动,未能实现聚并。随着气泡间距的增加,中间涡流需要提供的更大的向内作用力才能使气泡实现聚并,即气泡间距越大,气泡越难实现聚并。
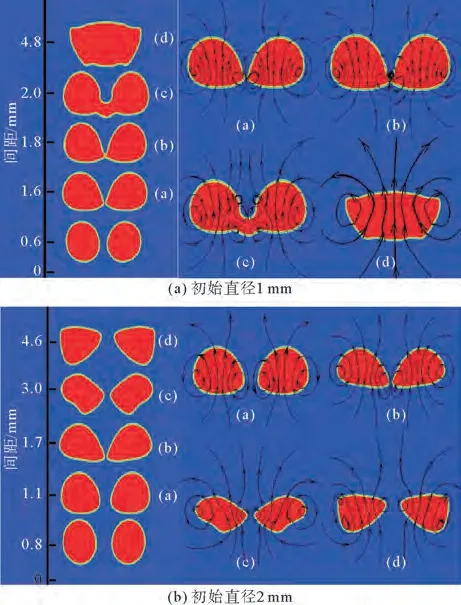
图7 等径气泡在不同间距下聚并过程及流线分布Fig.7 Coalescence process and pressure streamline distribution of equal diameter bubbles at different distances
图8给出了等径气泡不同间距下聚并过程中压力分布规律。对比初始阶段时压力分布发现,泡内压力分布基本一致,泡外压力分布受间距影响较大,低压区范围随气泡间距的增大而减小。泡内外压力差相同,但是在此压力差下产生的力不能将间距较大气泡实现聚并。随着气泡聚并上升,气泡形状发生变化,压力发生重排。
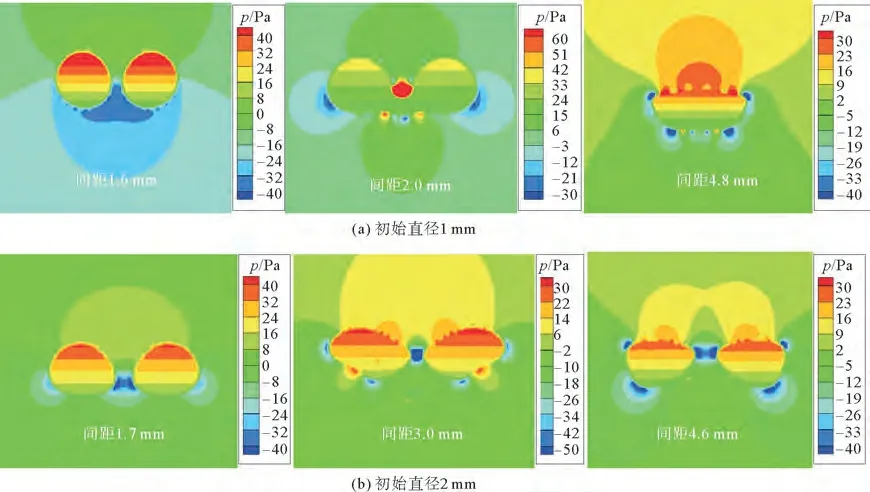
图8 等径气泡在不同间距下聚并过程的压力分布Fig.8 Pressure distribution in coalescence process of equal diameter bubbles with different spacing
通过对不同初始直径和间距下气泡的聚并过程研究发现,聚并规律不尽相同,气泡间距X决定了聚并的可能性。研究中发现在气泡聚并过程存在临界间距ΔX:当X≤ΔX时,气泡在涡流和压差的作用下实现聚并;当X>ΔX时,气泡间作用力减弱,不能实现聚并。图9是在不同模拟状态下聚并时临界间距与气泡直径关系。从图9看出,初始直径小于6 mm 时,临界间距受到液相黏度影响较大,黏度越大临界间距越小;在较低黏度下临界间距呈现先增大后减小的趋势;黏度较大时,临界间距随气泡直径变化较小,在0.4~0.6 mm 之间。
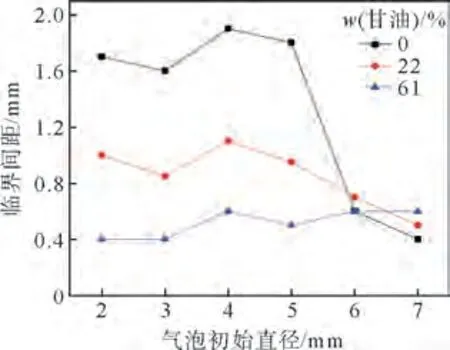
图9 甘油体系中不同气泡初始直径聚并过程中的临界间距Fig.9 Critical distance of coalescence of different bubble diameters in glycerol system
2.5 气泡聚并行为对传质过程的影响
主要考察初始直径为2,4,6 mm 等气泡,在气泡间距为1和2 mm 时聚并行为对传质过程的影响。图10是平行气泡聚并过程中不同阶段下CO2质量分数云图。从图10可以看出,气泡在聚并过程中,CO2不断向液相中传递,聚并前CO2浓度区主要分布在气泡底部,随着聚并过程的进行,CO2浓度区分布于气泡两侧和底部,颜色越深说明CO2浓度梯度越大。
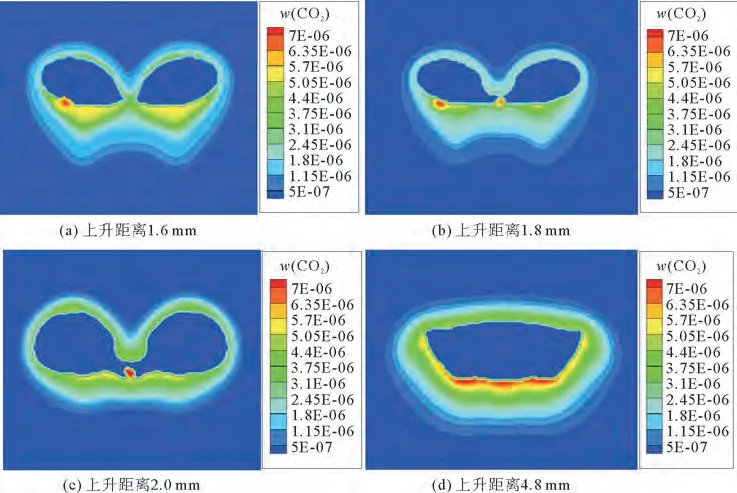
图10 平行气泡聚并过程中CO2 质量分数分布Fig.10 Distribution of CO2 mass fraction during coalescence of parallel bubbles
图11给出了不同直径气泡在不同间距下CO2溶解量变化规律。从图11可以看出,CO2溶解量随着气泡直径的增大而增大。初始直径为2和4 mm气泡,在间距为2 mm 时CO2溶解量高于间距为1 mm 时,这是由于间距在1 mm 时气泡发生聚并,聚并后导致气液接触面积减小造成的。其中,直径4 mm 气泡聚并后CO2溶解量减小了21.7%,2 mm 气泡减小了24.7%。初始直径为6和8 mm气泡,溶解量曲线基本重合,CO2溶解量没有明显变化,说明气泡未发生聚并行为。通过对不同直径气泡的聚并分析可知,气泡聚并行为使气液接触面积减小,导致CO2在水中溶解量减小。也就是说,在聚并过程中气液接触面积的大小对传质效率的影响起主要作用。
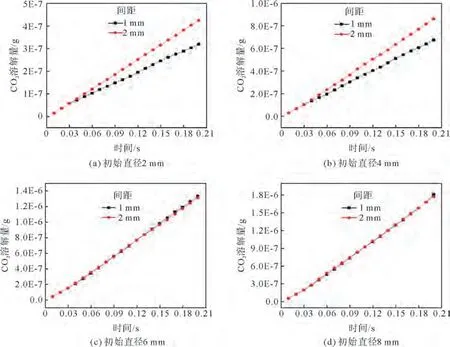
图11 不同气泡间距下CO2 溶解量变化Fig.11 variation of CO2 dissolution under different bubble spacing
3 结 论
1)聚并过程中气泡新产生多个涡流结构,涡流周围流线分布密集,速度较快,流场运动更复杂;泡内存在压力梯度,由于气泡表面形体曳力不对称分布造成气泡形状发生变化,压力分布重排,泡内压力值减小。
2)聚并距离受到黏度和气泡直径的共同影响。聚并距离随气泡直径的增大呈先减小后增大的趋势;随着液体黏度的增大,流动阻力增大导致聚并距离随黏度增大而增大。
3)在涡流和压力差的作用下气泡实现聚并,但是间距决定了聚并的可能性。研究发现了不同浓度甘油溶液中临界间距与气泡直径的关系,直径小于6 mm 气泡黏度越大临界间距越小;直径大于6 mm气泡受黏度影响较小,在0.4~0.6 mm 之间波动。
4)气泡聚并行为使气液接触面积减小,导致CO2溶解量减小。通过模拟定量测定了直径4 mm气泡聚并后CO2溶解量减小了21.7%,2 mm 直径气泡减小了24.7%。
