树状支撑单层网壳支撑点分布形态优化研究

赵洋立

（重庆市设计院有限公司，重庆 400015）

0 引言

树状结构具有节约人员活动空间、外观轻盈、构件截面较小等优点，近年来在实际工程中的应用越来越多。树状结构也被称为树状支撑、树状柱，其节点几何数据具有树状数据结构，与其他竖向受力构件相比有两个特征：一是同级节点之间没有构件连接；二是上端为对平面受力结构的多点支承，下端为单点刚接支座。

近年来，针对树状结构的相关研究与实践成果越来越多，但大部分研究主要着眼于基于应变能的树状分叉点的几何位置优化[1]，而树状结构本身的生成方法主要受建筑师影响或依赖于数学公式；有关树状结构的形态生成方法与结构经济性关系的文章[2]则较为少见，而支撑点的分布、排列方式直接影响树状支撑的最终优化形态。

结构形态创构方法是一种由传统结构形式向自由、灵活、合理方向转变的途径之一，也是结构设计方法由偏经验向偏理论转变的有效方法，同时还是建筑空间感受与力学合理性相协调的手段。该方法的理论进一步发展与成熟，将为人们提供崭新的活动空间，带来与自然和谐共存的环境。

随着计算机技术的发展，数值找形方法逐渐受到人们重视。半谷教授将“广义逆矩阵”理论应用到柔性结构初始形状确定问题，且提供了利用机动体系的特点创构出结构形态的可能性。名古屋大学教授大森针对悬挂薄膜等柔性结构形态创构方法，实现了逆吊试验理论化方法。上世纪90 年代初，Xie 与Steven 模仿自然界的进化规律提出了“ESO 方法”，目前该方法在机械工程领域被广泛应用。近几十年来众多的学者相继提出了很多分析方法，如“均质化方法”“Bubble 方法”“遗传算法（GA）”“基结构法（GSM）”“粒子群算法”等。这些数值分析的方法目前虽然还没有成熟，不能应用到实际工程中，但对结构形态创构理论与方法的进一步探讨与深入研究打下了良好基础。“改进进化论方法”“高度调整法”“杆系结构形态创构方法”已应用到实际工程中，得到了较高的评价。其中，“高度调整法”是利用应变能对节点坐标的敏感度特性逐步调整形状的方法来获得“轻而刚”的连续壳形状的方法。

基于敏感度的杆系结构形态创构方法[3]（下文简称“渐进法”）是针对杆系结构，利用单元、节点坐标参数与结构应变能的关系，提出能够兼顾拓扑与形状的杆系结构形态创构方法。该方法基于有限元平衡方程，分别计算节点自由移动、约束移动、单元增加和单元消除等四种应变能敏感度，并利用这些敏感度与应变能变化关系生成或修正结构的拓扑形状，调整节点位置，最终得到应变能最小的合理结构形态。

而逆吊递推找形法[4]（下文简称“逆吊法”）的实施步骤可概括为:首先找到各级树枝所承担的屋面区域的受荷中心，然后依次令各级树枝指向其分担的屋面受荷中心，最后通过逐级递推建立树状结构的几何形态。

本文着眼于结构模型生成阶段，运用“渐进法”与“逆吊法”尝试探讨支撑点分布位置的优劣。

1 试验过程

1.1 支撑形式选择与生成方法

树状支撑结构的几何特征可以用树状数据结构来描述。在描述过程中我们发现，每个分叉点的数据包含以下几个方面：父节点的编号、本节点的编号、本节点的坐标、本节点的分支度量（分支度）。可以预见的是，在优化设计阶段，除了最末端的节点位置外，其他节点的坐标都会改变。所以生成阶段需要关注的数据是节点的分支度量、末端节点（叶节点）的几何坐标、各节点之间的父子关系。

现有结果表明，“二叉树”分叉点处父杆件与两个子杆件共三个方向的向量几乎共面。这样的后果是该部分父杆件与子杆件组成的子结构存在一个“平面外”失稳的屈曲模态，由于每个节点都有各自的屈曲模态，整体结构则有较高的整体失稳风险。

面对这样的风险，可以预见的是，在进行屈曲分析之后，“二叉树”结构的杆件截面将有“平面内”和“平面外”的区别，“平面外”方向截面惯性矩的增加将引起承载力的浪费，增加工程造价。相比之下，“三叉树”结构就不存在这个问题，故本次试验生成的模型节点分支度为3。

模型生成过程中还应着重关注末端节点（叶节点）的几何坐标、各节点之间的父子关系。而由于节点父子关系千变万化，因此本次试验仅指定一种节点父子关系。

1.2 计算模型的生成

1.2.1 初始条件

试验基本模型为单层网壳与层数为2（所有叶节点深度为2）的“满三叉树”树状支撑，其形态与几何尺寸如图1 所示。为了减小构件离散对支撑点的影响，故取网壳中每个三角形边长为0.43m，并使构件截面为400×4mm 的矩形。

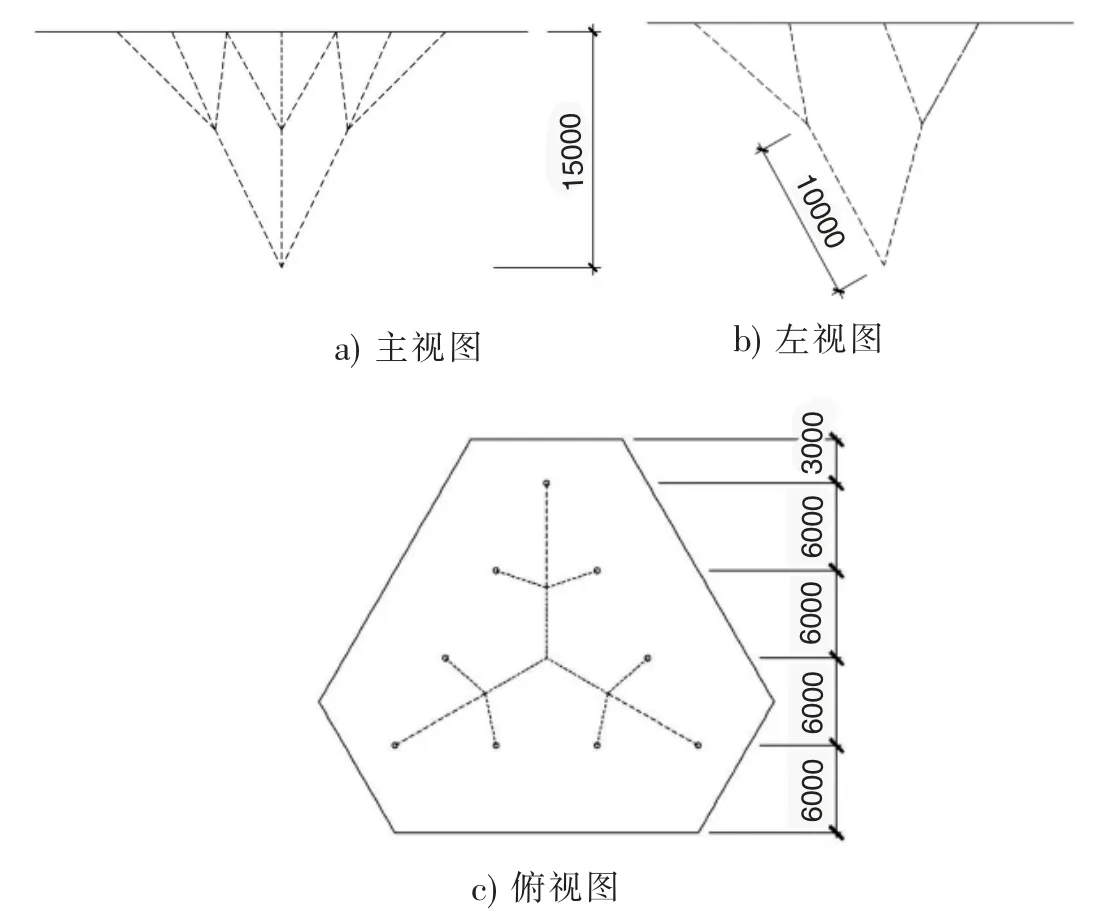
图1 初始模型三视图

若保证网壳面外刚度不变，此时该布置可等效为网格大小为2m，截面为400×130×5mm 方钢管组成的网壳。所有构件均为6 自由度的梁单元。单元的截面与材料见表1。

表1 构件截面与材料

为了比较支撑点位置的优劣，以7 组算例为试验素材，每组算例之间的区别在于α 角的大小，如图2 所示。

图2 参数与生成方法示意

每组算例内含有两个计算模型，一个是初始形态模型，初始形态的分叉点E 的坐标在ABC 的平均坐标D 与O 点的连线上，距离O 点10m，如图3 所示；另一个是用优化方法调整过分叉点（阶度为2 的节点）位置的模型。

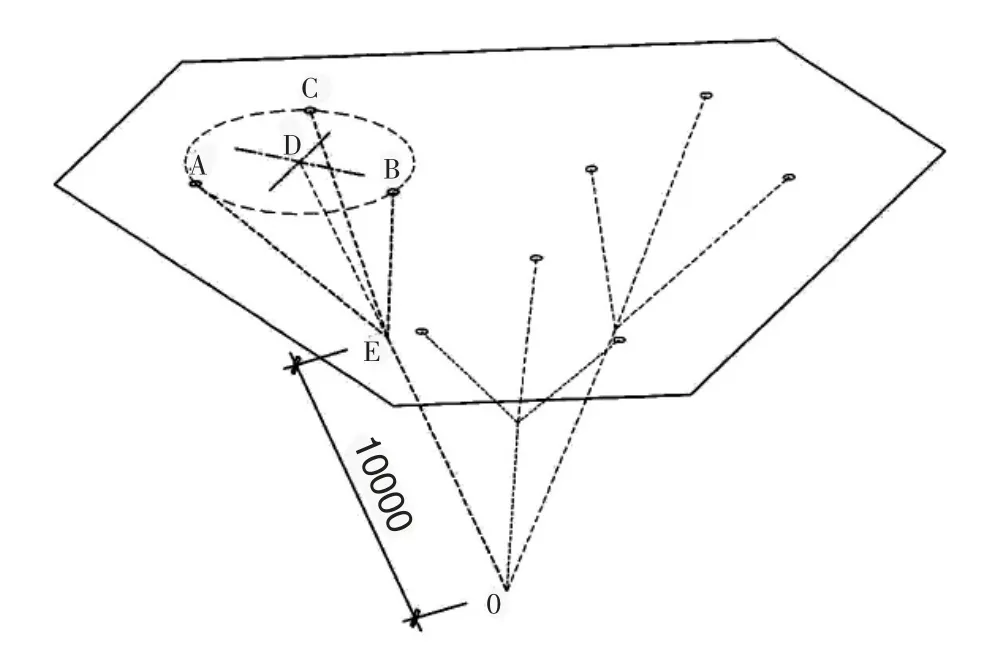
图3 初始形态分叉点的生成

调整方法为基于应变能敏感度的渐进法[3]与逆吊递推找形法[4]。“渐进法”是通过迭代计算，调整节点坐标，利用节点坐标与总应变能的相关性，引入数值阻尼，以最小应变能为目标，使节点坐标收敛的方法。“逆吊递推法”是利用树状支撑杆件无弯矩的特点，运用形-力关系求杆件方向量，进而确定节点坐标的方法。

由于两种方法的优化结果非常接近，差异非常不显著，所以下文中不再区分使用的优化方法。

以A 组为例，两个模型的外观差异如图4 所示。

图4 初始形态与优化形态的外观差异

1.2.2 边界条件

树状支撑底部，即根节点为6 自由度固接，叶节点所在杆件的末端（上端）释放所有自由度，其余构件之间完全刚接。为尽量减小网壳离散性带来的影响，叶节点附近的节点设置了刚性连接，如图5 所示。

图5 刚性连接约束示意

结构考虑自重和网壳上的z 轴负方向均布荷载。

1.3 求解方法

本试验采用midas gen V2019 的整体解决方案，包括模型搭建、求解器、数据提取等。

2 技术分析

2.1 初始形态与渐进优化后的应变能对比

图6、图7 展示了每组算例初始形态与优化形态之间的应变能。为了方便对比，基于最小值做了归一化处理。

图6 初始形态与优化形态的总应变能对比（原始数据）

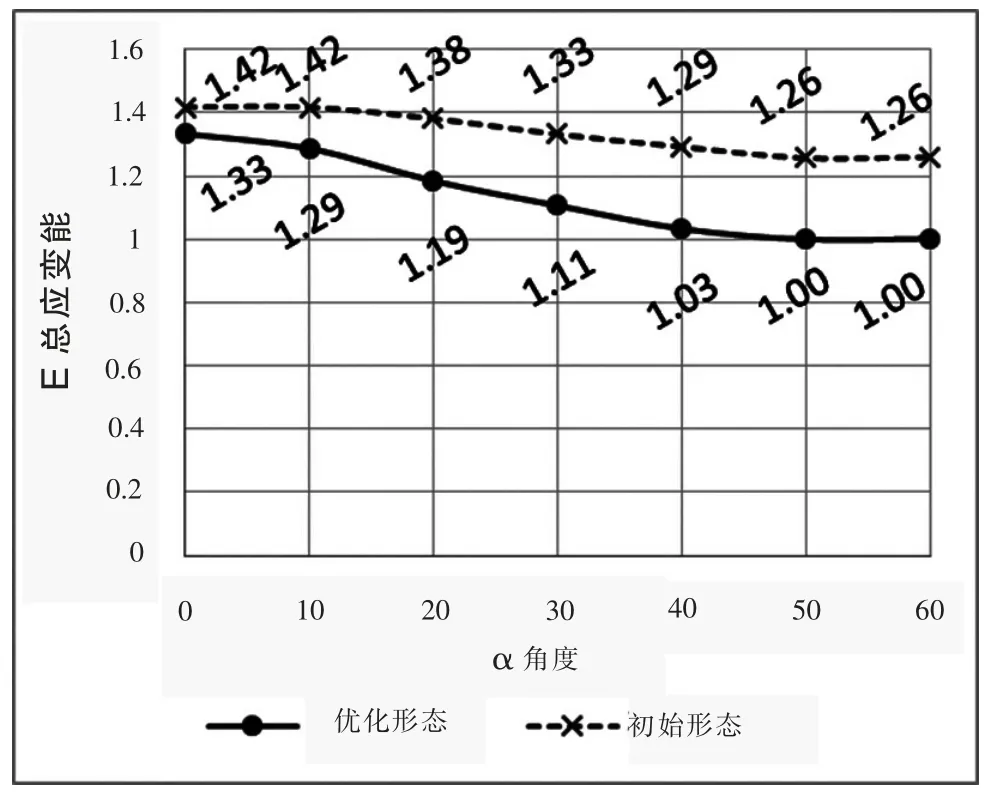
图7 初始形态与优化形态的总应变能对比（归一化处理）

可以看到的是，优化的效果较为显著。总应变能平均下降15%，最大下降21%（α=60°），且数据变化趋势合理。这表明上文提到的优化方法较为合理，具有实用价值。

2.2 总应变能、树状支撑应变能对比

图8 展示了每组算例的总应变能与支撑部分应变能。为了方便对比，基于最小值做了归一化处理。

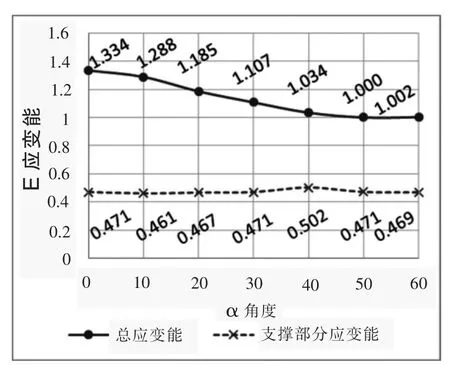
图8 总应变能与支撑部分应变能对比（归一化处理）

可以看到的是，总应变能与支撑部分应变能之比平均为2.4，即网壳部分应变能是支撑部分的1.4 倍。其中，α=50°算例的总应变能最小，且差异显著；α=10°算例的支撑部分应变能最小，但差异不显著。

2.3 支撑点分布与应变能的规律探讨

α=40°～60°时，其总应变能较小，变化也不大，而α=0～10°时总应变能较大。所有总应变能数据的相对极差为29.4%，相对标准差为11.2%，变化较为显著。所有支撑部分应变能数据的相对极差为8.76%，相对标准差为2.62%，相比于优化的幅度21%，并不显著。就这几项数据而言，α=40°～60°的模型在所有算例当中相对更优。

总应变能变化较大，但支撑应变能变化较小。通过观察α=10°与α=40°的模型，笔者发现α=0～10°时，网壳三条长边形成的悬挑段长度较大，使得边缘区域的网壳节点的z 向刚度较小。那么在统计总应变能时，悬挑部分的贡献就有相当大的占比。而α=40°时，各个区域的z 向变形相对均匀。

基于朴素的工程经验判断，网壳的面外刚度直接影响结构的总应变能。

2.4 改进与进一步讨论

当我们观察到支撑点的分布影响的总应变能，这种影响可能是间接的，通过其他中间变量影响的。如果存在这样一个中间变量，我们将其与支撑点的分布位置脱钩，就会使得支撑点分布与总应变能脱钩。

笔者猜想，只要将z 向变形的均匀程度大幅提高，就可能排除支撑点分布对总应变能的影响。如果试验数据的相对标准差大幅缩小，就表示算例之间总应变能的差异并不是直接由支撑点的位置控制的，而是由z 向变形的均匀程度控制的。

为了验证这个猜想，将网壳的面外刚度放大10 倍，以模拟带腹杆的网架结构与树状支撑共同工作的表现，由此判断支撑点分布的优劣差异是否对网壳面外刚度敏感，如图9、图10 所示。

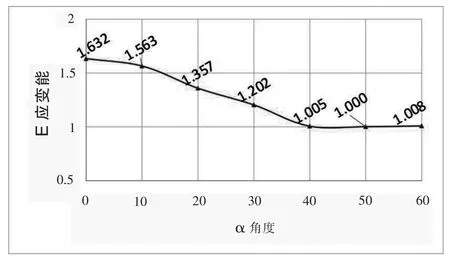
图9 未增大面外刚度的算例中网壳部分应变能（归一化处理）

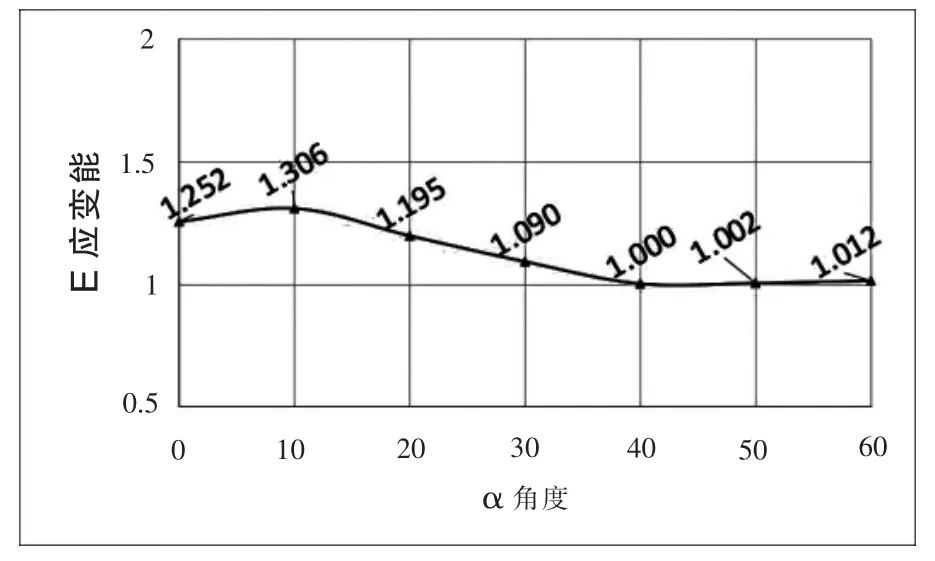
图10 增大面外刚度的算例中网架部分应变能（归一化处理）

α=40°～60°时，其总应变能相对较小，差异不显著。所有总应变能数据的相对极差为8.3%，相对标准差为3.8%。相比于上一组“柔性”网壳算例，相对标准差由11.2%缩小到3.8%，下降了63%。这表示网壳面外刚度大幅提高后，支撑点的布置与总应变能之间的相关性显著下降。

所有支撑部分应变能数据的相对极差为3.6%，变异系数（相对标准差）为1.2%，差异不显著。网壳（网架）部分应变能的标准差由20.0%下降至10.6%，下降显著。

由此印证了支撑点分布对总应变能的影响，对网壳面外刚度敏感。进一步讨论可以发现，对于面外刚度较大的网架结构，支撑点的分布对应变能的影响不大；对于面外刚度较小的单层网壳，支撑点的分布对总应变能的影响显著。

3 结论

就本文所指定形式的树状支撑结构而言，在特定角度时总应变能较小，对于面外刚度较小的单层网壳，支撑点的分布对总应变能的影响显著；对于面外刚度较大的网架结构，支撑点的分布对应变能的影响不大；每个支撑点分担荷载的均匀程度可能与总应变能负相关。由此可见，对于单层网壳与树状支撑组合形成的结构，优化支撑点的分布位置能显著提高结构合理性、降低材料用量，换言之，对支撑点分布位置的优化十分必要。