基于改进樽海鞘群算法的PMSM变论域模糊控制
2022-07-27金爱娟冯雅茹李少龙
金爱娟,冯雅茹,李少龙
基于改进樽海鞘群算法的PMSM变论域模糊控制
金爱娟,冯雅茹,李少龙
(上海理工大学,上海 200093)
为提高自动化包装流水线的生产效率,针对永磁同步电机PI控制器参数无法适时调整而引起的稳态误差较大、抗干扰性差等问题,提出一种基于改进樽海鞘群算法的新型变论域模糊控制器。通过游走策略和变异分布策略对樽海鞘群智能算法的位置更新进行改进,同时加入过界个体的加权位置修正与劣势个体二次迁移,并将优化后的算法与变论域模糊PI控制器相结合,用于调节伸缩因子,以获得对永磁同步电机更好的控制效果。仿真表明,文中改进后的控制器较传统PI控制器有效减小了静态误差;同时优化后的控制器令PMSM在变速和变载工况下响应更快,较改进前的樽海鞘群算法作用下PI控制器在变速和变载工况下的超调量分别降低约21.35%和62.85%。算法优化伸缩因子后得到的变论域模糊控制与其他控制相比,更有效地提高了系统的鲁棒性,改善了系统的控制性能,减小了损耗。
永磁同步电机;变论域模糊控制;樽海鞘群算法;伸缩因子
如今人们的日常生活已离不开包装,任何商品在生产、储存、运输等阶段都离不开不同程度的包装工艺,产品在转手到消费者手中也更需要被包装,因此市场上可将包装分为消费者包装、产品包装、运输包装3类,不同类别的包装在材料制作工艺及包装流程上均有不同。随着国民经济稳定且持续的增长,人均收入不断提高,国民消费升级和消费规模扩大是一种必然的趋势,这也带动着包装行业的市场空间将不断地扩大。随着科技的发展,如今出现了更多的自动化流水线,利用自动化设备进行各种花样的包装已经成为包装产业的主流。
永磁同步电机(Permanent Magnet Synchronous Motor,PMSM)具有体积小、效率高、结构简单、操作方便等优点被广泛使用在包装机上。此外,在化工、食品、日化等多个领域上,永磁同步电机都发挥着重要的作用。永磁同步电机的无位置传感器算法由于摆脱了传统传感器体积大、成本高、使用环境受限等缺点而成为如今的研究重点。在闭环估算算法中,通过建立合理的观测器观测估算电机运转中实际的电流值,再反馈给电流环计算出电流误差值,控制器将根据电流误差进行调节[1]。由于PMSM系统具有变参数、强耦合等非线性特性,在无感控制的基础上,电机对控制器的精度要求也会更高。此外在包装系统中会存在一些非人为因素的影响,如电机的负载突变导致电流过大、转矩波动,环境温湿度不适造成电机内部损耗等,都会影响包装机在生产环境中的控制精度,甚至危害电机本体。因此对电机控制器的研究与优化一直是个热门话题。
传统的比例–积分–微分控制器(Proportion Integration Differentiation, PID)控制方法不用基于模型,操作简单,但在系统运行中它参数固定,无法对误差的变化进行合理的跟进、调节,在对复杂、具有大惯性的对象的控制上有很大的局限性,因此学者们在对PID控制方法的改进上做了大量的研究。高靖凯等[2]采用传统PID控制与单神经元PID控制相结合的方法,单神经元PID对非线性系统进行控制,传统PID在稳态情况下误差较小,两者的结合进一步减小了永磁同步电机在控制过程中的转矩脉动和转速脉动。张魏等[3]将一种负载转矩前馈补偿与单神经元PID相结合,通过前馈补偿改善系统的抗干扰能力,通过单神经元PID增强速度控制的鲁棒性。王福杰[4]对比了模糊PID控制(Fuzzy PID control)与神经网络PID控制2种方式对永磁同步电机的控制性能,结果表示,模糊PID在实时性方面较神经网络PID控制更具有优越性。李洪兴[5]首次提出的变论域模糊(Variable Universe Fuzzy, VUF)控制,它对模糊控制有了更进一步的改进。变论域令模糊控制具备了自适应调节的能力,其中的伸缩因子参数的确定对控制器调节能力有很大的影响。
樽海鞘群算法(Salp Swarm Algorithm,SSA)于2017年被Seyedali MIrjalili等提出。樽海鞘群算法是一种较为新颖的群智能优化算法,该算法的灵感来源于深海中的樽海鞘链的生存行为[6]。在种群移动过程中,樽海鞘以链式相互连接,分为领导者和追随者。领导者不停地朝着食物进发,并引导身后的追随者,而追随者的移动也将仅受前一个个体的影响和制约。该移动模式下的算法计算量小、结构简单且收敛速度极快,因此被众多学者研究。范千等[7]将折射反向学习和自适应控制因子运用到SSA算法中,以提高算法的收敛速度和精度。陈忠云等[8]将种群分为3个子群,对各个子群进行优化,并引入非均匀高斯变异,使算法在求解高峰多维函数上具有更好的性能。刘景森等[9]入了帕累托分布和混沌映射来提高全局搜索能力,并将随机交叉策略用于提高算法的局部探索能力,提高了算法的搜索精度。王梦秋等[10]利用冯诺依曼拓扑结构与自适应评估策略对SSA算法改进,并将改进后的算法运用于对PMSM的参数辨识中,提高了信号跟踪性能。
受上述文献启发,文中提出了一种基于布朗游走等策略的改进樽海鞘群算法(SSA Using Brownian Wandering and so on, BWSSA),具体步骤:将全局开发能力强大的布朗随机游走策略与SSA领导者位置更新相结合,在保留原个体特性的基础上加强了领导者的勘探能力;在追随者位置更新中引入分布变异,并加强与当前最优个体的学习交流能力;提出了利用加权重心的位置修正策略,并运用于过界个体的位置更新之中,以解决将过界个体放置在边界造成的空间中个体分布不均的问题,增加位置更新的随机性;参考自然界生物觅食特性,设定追随者后半部分个体为具有迁移可能性的劣势个体,进行二次位置更新,判断优劣并作保留。
BWSSA算法是对SSA算法进行了合理的改进,以解决SSA易陷于局部最优的问题,使得在复杂函数的寻优上更具有优越性。将传统SSA算法和优化后的BWSSA算法分别与变论域模糊PID控制相结合,得到基于BWSSA的变论域模糊PI控制(Variable Universe Fuzzy Control Based on BWSSA, BWSSA- VUFPI)和基于SSA的变论域模糊PI控制(Variable Universe Fuzzy Control Based on SSA, SSA-VUFPI)。利用优化后的算法可对伸缩因子参数进行更精确地掌控,用于永磁同步电机无位置传感器[11-12]上,以提高电机无感控制下的动态性能。
1 永磁同步电机的数学模型
表贴式永磁同步电机在同步旋转坐标系–下的数学模型建立见式(1)。
(1)
式中:u、u和i、i分别为在–轴上的定子电压和电流分量;e为转子的电角速度;为定子绕组电压;φ、φ分别为定子磁链在–轴上的分量,用方程(2)表示。
(2)
式中:L、L分别为–两轴上的电感分量;f为永磁体磁链。将式(2)带入式(1)可得到定子电压表达式(3)。式(3)实现了三相永磁同步电机的完全解耦,更便于后期对控制器的设计。
(3)
PID控制器即通过控制p、i、d这3个参数对速度环传递的速度误差进行比例–积分–微分调节,将转速信号转换为电流信号传递给式(3)。虽然PID控制器中的微分调节能对误差信号做出更快速响应,但易引起高频震荡、噪声放大,且参数调节难度大,因此一般工业控制都会采用PI控制器控制方法。后文也将以PI控制器为基础进行研究对比。
2 变论域模糊控制
传统的模糊PI控制即在PI控制器的基础上添加的模糊规则库,根据库中数据实时地输出合适的PI参数。根据提前设定好的模糊规则库,将输入误差及其变化率传入库中进行模糊推理,即可对PI的2个参数p、i进行实时调整[13]。模糊控制器鲁棒性较好、操作简单,同时也非常依赖专家知识。在一定的论域范围内,过多的控制规则在精确系统输出的同时也增加了系统复杂程度,过少的规则虽然简化了系统但输出效果不理想。
变论域模糊PI控制便是在此基础上,利用伸缩因子对模糊控制器中的论域进行自适应调整,从而修正模糊控制过于依赖初始论域这一缺陷。伸缩因子作用下的变论域原理见图1,为伸缩因子,[−,]为模糊控制的论域。当控制器的输入量增大或减小,伸缩因子随之发生变化,并实时地控制论域伸缩。变论域方法在不改变控制规则数量的情况下,提高了控制器的精度。
在双输入的控制系统中,输入变量偏差与偏差变化率c均会作用于伸缩因子,伸缩因子对整个变论域系统有着极大的影响。定义输入输出量的论域见式(4)。
(4)
图1 变论域原理
Fig.1 Schematic diagram of variable universe
式中:,分别为输入变量偏差和偏差变化率c的伸缩因子,[−,]和[−c,c]分别为两者的初始论域。文中设定模糊语言变量均为{NB,NM,NS,ZO,PS,PM,PB}。通常采取基于函数设计的伸缩因子,表达为:
(5)
由于整个系统的目标为误差趋近于0,可知该伸缩因子的变化率与变量偏差成正比,然而式(5)中参数难以确定最佳值,因此文中将采用优化后的BWSSA算法直接对伸缩因子进行优化。
3 SSA算法优化
在SSA算法中,领导者的位置更新为:
(6)
式中:x为第只樽海鞘个体在第维度上的位置;F为在第维度上的食物位置,该值在每次迭代中都会更新为当前种群中适应度最佳的个体位置;b和b分别为维度空间对应的上届和下届;1、2、3为3个控制参数,其中2和3是[0,1]内的随机数,1满足式(7)。
(7)
式中:为当前迭代次数;为整个寻优的最大迭代次数。
SSA算法中的追随者位置紧随前一个体,因此符合牛顿运动定律,其位置更新为:
(8)
(9)
第(≥2)个体(追随者)在第维的位置表示为:
(10)
3.1 BWSSA算法设计
3.1.1 布朗游走领导者位置优化
樽海鞘群算法中领导者位置更新过于依赖当前食物位置,丧失了个体的多样性与主动性。海洋捕食者算法(Marine Predators Algorithm,MPA)于2020年被Afshin等[14]提出,该算法基于海洋适者生存理论,模拟了捕食者在捕获猎物过程中的游走模式,将迭代分3期,不同时期采取不同的随机游走策略[15]。在迭代初期,捕食者着重于勘探策略,通过布朗游走获取移动步长。将MPA算法的布朗游走理论与SSA领导者位置更新机制相结合,使领导者随机地朝着食物的方向移动,满足式(11)。
(11)
其中:
(12)
其中,s为第个体(领导者)在维的移动步长;R为呈正态分布的布朗游走随机向量;F为当前食物位置上维的值;为[0,1]内随机向量;用于控制步长。
3.1.2分布追随者位置改进
为了打破个体盲目跟随、陷入局部最优的局面,在追随者位置更新中引入分布扰动和与最优个体的信息交流。分布的自由度参数为当前迭代次数,随着迭代增加,自由度增大进而变异幅度改变。=1时,分布即为柯西分布;随着(→∞)→(0,1),它的分布状态逐渐由前期的柯西分布趋向于后期的高斯分布。柯西分布可增强算法的全局探索能力,有效地保持了种群的多样性;高斯分布可增强局部开发能力,保证算法后期的收敛速度[16]。分布扰动可以帮助算法跳出局部最优解,加快它的收敛。改进后的领导者位置更新机制表达为:
(13)
3.1.3 过界个体加权位置修正
通常情况下,过界个体位置修正是将超出空间范围的个体直接放置在边界上,这会造成空间中个体分布不均,个体不够灵活,因此文中提出基于加权重心[17-19]的修正过界个体位置的方法。
计算加权重心见式(14)—(15)。
(14)
(15)
式中:x为种群中第个体位置;worst为当前适应度最差个体的位置,适应度较好的个体权重较高。
此外再引入自由落点设定。迭代前期增加了算法的全局探索能力,位置更新的自由随机性更大;随着迭代的推进,算法由全局探索逐步倾向于局部开发,随机性逐渐减弱,对加权重心的依赖性增强。合理的调整自身随机性和重心依赖性,可确保不改变空间原上下部分的个体浓度。整个的位置修正设定可用式(16)表达。
(16)
3.1.4 尾端劣势个体二次迁移
在自然界中,距离食物极远的生物为了确保生存会主动迁移至更优位置。参考这一特性,设置追随者群体中的后半部分个体为劣势个体,劣势个体具有潜在的迁移可能性,该部分个体同样根据式(16)进行随机位置更新,若更新后的位置更靠近食物,则保留该迁移位置;否则移动到原位,等待下一次迭代。
3.2 BWSSA算法性能评估
改进后的BWSSA算法具体流程见图2。在初次运行中,初始化种群的参数和个体的初始位置,计算适应度并排序,选出最优个体作为食物。随后根据式(11)—(13)更新个体位置,劣势个体将有二次迁移的可能。待个体位置更新完毕后对过界个体按照式(16)进行位置修正,随后根据适应度对个体排序,并更新食物位置。若不满足输出条件则再次进行迭代,直至满足终止条件或迭代次数达到上限。
为验证BWSSA算法的性能,引入SSA算法、MPA算法进行对比实验,设置种群规模=25,最大迭代次数为500。测试函数选择单峰可分基准函数(Quartic)、多峰不可分基准函数(Ackley)、多峰不可分基准函数(Griewank)、多峰可分基准函数(Rastrigin),具体信息见表1。

图2 BWSSA算法流程
为了实验的准确性和算法优化的有效性,将每种算法在表1中测试函数上独立进行10次寻优实验,并从结果中获取平均值、最优值等。若一次实验的最优值满足,则判定该次实验成功,其中为当前实际求得的最佳值,best为理论上函数的最佳值。实验成功率用表示,最终实验结果见表2。
从表2中可以看出,BWSSA算法结合了SSA快速寻优和MPA准确寻优的特点。在对单峰函数(1)求解时,BWSSA求解精度远高于SSA算法和MAP算法;在对多峰函数(2、3、4)求解时,BWSSA算法不仅能寻得理论最优值0,它的速度也比同样寻得理论最优值的MPA算法快了1倍。由此可见,BWSSA算法在多种寻优问题中,尤其在多峰值函数的寻优中具有良好的表现。
通过图3可以更直接地看出,BWSSA算法在多峰函数的寻优中不易陷入局部最优,在单峰函数的寻优中也比SSA算法和MPA算法的收敛速度更快,搜索精度更高,整体性能更优。
表1 基准函数信息

Tab.1 Benchmark function information
表2 基准函数优化结果对比
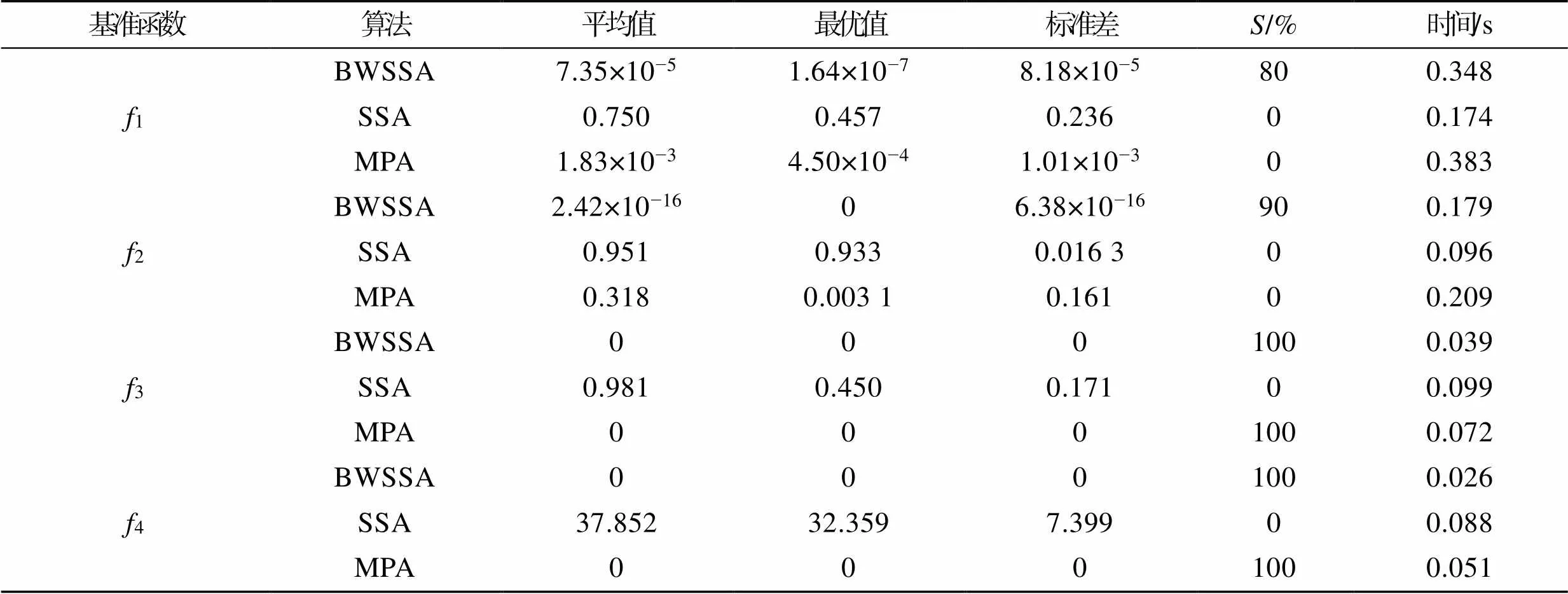
Tab.2 Comparison of optimization results of benchmark functions

图3 基准函数优化曲线
4 基于BWSSA算法变论域模糊PI的PMSM无感控制
将上述BWSSA算法与变论域模糊PI控制相结合,得出基于BWSSA算法的变论域模糊PI控制器模型见图4。算法会根据输入变量及其变化率来动态地调节伸缩因子,进一步控制模糊控制器的论域适时变化,由此输出更适合的PI变化参数(Δp、Δi),与设置好的PI基础参数(p、i)相结合后传入控制器,以完成优化。
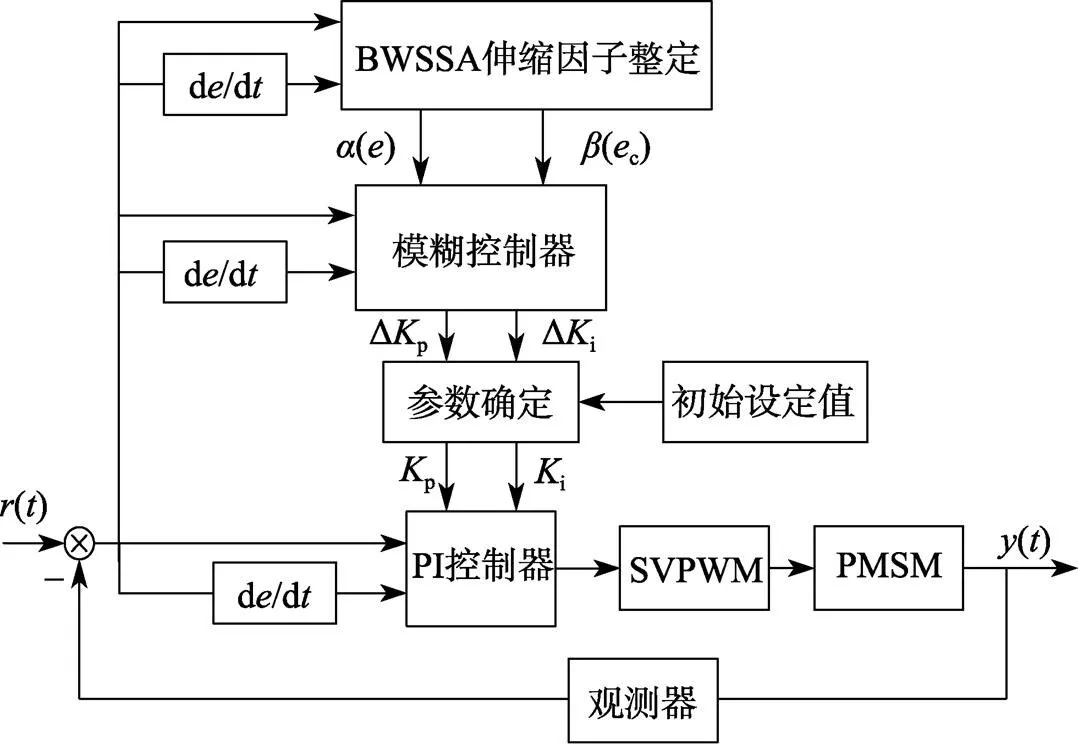
图4 基于BWSSA的变论域模糊PI控制器
基于BWSSA的变论域模糊PI的PMSM无传感器控制框图见图5。根据图5所示的系统框图搭建模型,转速外环由BWSSA–VUFPI控制器控制,以提高系统调节转速与抗负载变化的能力[20]。为了进一步验证BWSSA–VUFPI控制器在无感PMSM控制中的优越性,将它与传统PI控制器、Fuzzy–PI控制器、SSA–VUFPI控制器进行实验对比。通过Matlab/ Simulink环境搭建模型,仿真中的永磁同步电机主要参数:电感值为2.05 mH,电阻值为1.325 Ω,摩擦因数为0.025 N·m·s,永磁体磁链为0.225 Wb。
从以下2个方面对BWSSA算法优化变论域模糊PI控制器进行分析。
1)空载实验。电机以100 r/min低速空载启动,在0.3 s时给定转速突变为高速1 000 r/min,该实验用以验证基于BWSSA算法的变论域模糊控制器是否具有更好的动态性能。
2)变载实验。电机给定转速恒为600 r/min,先以轻载1 N·m启动,在0.3 s时负载突变为3 N·m,该实验用以验证在有外界存在干扰且干扰不固定的情况下,优化后的控制器是否具有更好的鲁棒性。
4.1 空载实验
在此次实验中,电机先以低速(100 r/min)启动,在0.3 s时转速突变为高速(1 000 r/min)。将仿真结果进行整理分析,得到该电机的性能指标见表3,平均仿真结果见图6。
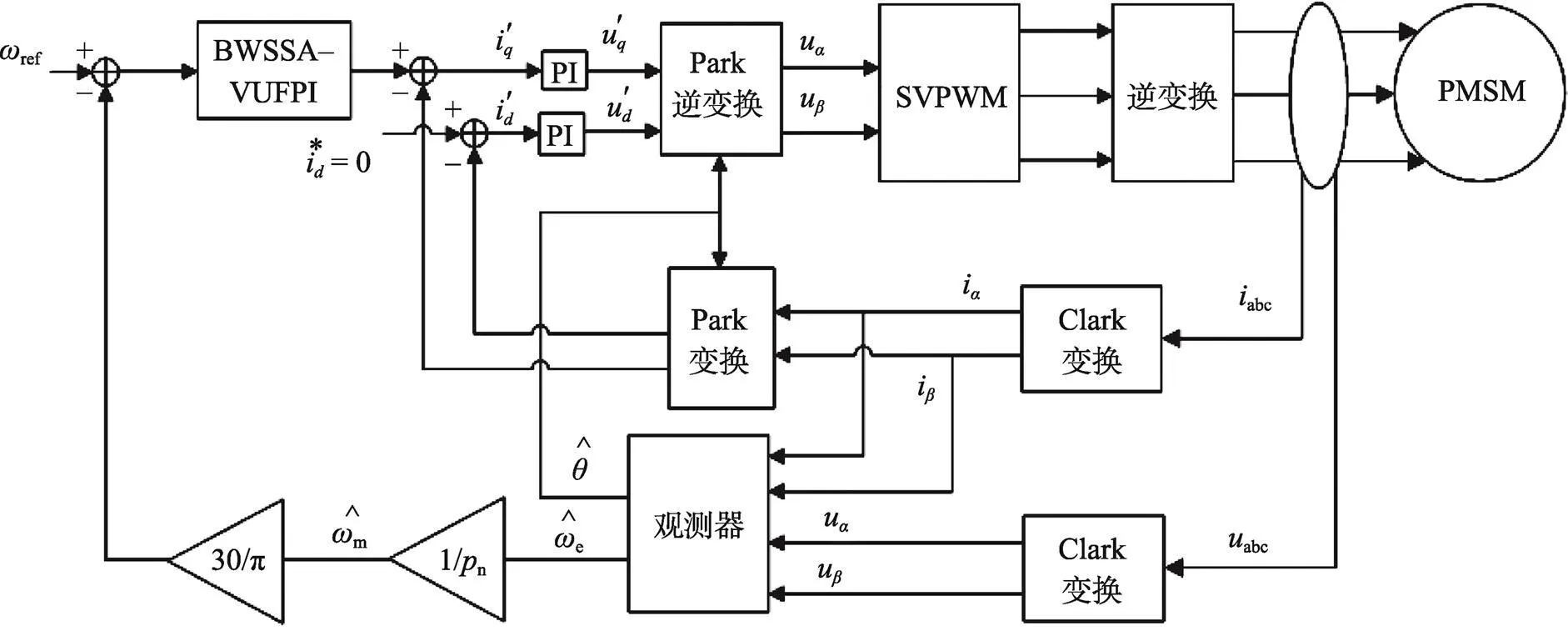
图5 基于BWSSA–VUFPI的PMSM控制框图
表3 空载变速实验电机性能指标

Tab.3 Motor performance index in no-load variable speed
分析表3可知,在BWSSA–VUFPI控制下的电机启动时的调节时间略长,比PI控制器慢了约0.02 s,但BWSSA–VUFPI控制下电机的稳态误差和超调量都比PI控制器与Fuzzy–PI控制器作用下的电机要好很多,尤其稳态误差较PI控制器小了约1 r/min,超调量较SSA–VUFPI控制器小了约34.15%,且BWSSA–VUFPI控制器作用下的电磁转矩在启动时的波动峰值也较其他2个控制器高,初步证明BWSSA–VUFPI控制器在控制电机低速运行时的稳定性。当0.3 s时电机转速突变为高速,BWSSA– VUFPI控制器作用下的稳态误差仅为1.53 r/min,其转速超调量0.205%小于另外3种控制器作用下的超调量,比SSA–VUFPI控制器作用下约小27.56%,且调节时间较短,电磁转矩在转速突变时也较SSA– VUFPI控制器高约21.35%。
由图6a可以看出,与其他3种控制器相比,BWSSA–VUFPI控制器作用下的PMSM在低速启动和变为高速时的转速波形更加平稳,反应快、误差小,几乎无超调,图6b显示出变速时的转矩脉动也较平滑,恢复较快。另外图6c显示出优化后的控制器对无感系统中的转速跟踪有一定的影响,例如在BWSSA–VUFPI控制器作用下,电机转速在突变为高速时的最大转速估算误差仅约200 r/min,较PI控制下的误差小了约1/3。
4.2 变载实验
在该实验中,电机以恒速600 r/min转动,初始电机带以1 N·m轻载启动,待到0.3 s时加重载至3 N·m。根据仿真结果整理出电机性能指标见表4。结合表4可知,BWSSA–VUFPI控制器作用下的电机各项性能指标都较另外2种控制器要好。在0.3 s时外加负载提升为3 N·m,BWSSA–VUFPI控制下的转速波动极小,超调量仅为0.354%,较SSA–VUFPI控制器作用下减小约62.85%,可见在电机经受外界干扰时,由BWSSA算法优化过的变论域模糊控制器具有较优的调节能力,可提升整个系统的鲁棒性。
由图7a可看出,在电机以1 N·m启动时,BWSSA–VUFPI控制器作用下的电机转速平缓上升至600 r/min,调节时间较短且稳态误差和超调量都极小,通过波形细节也可看出其稳定性。图7b中电磁转矩脉动波动小、波形平缓、恢复较快。此外图7c表现出在变载实验中,BWSSA–VUFPI控制器更利于无传感器系统中观测器对实际转速的跟踪,转速误差较小,转速跟踪较稳定。
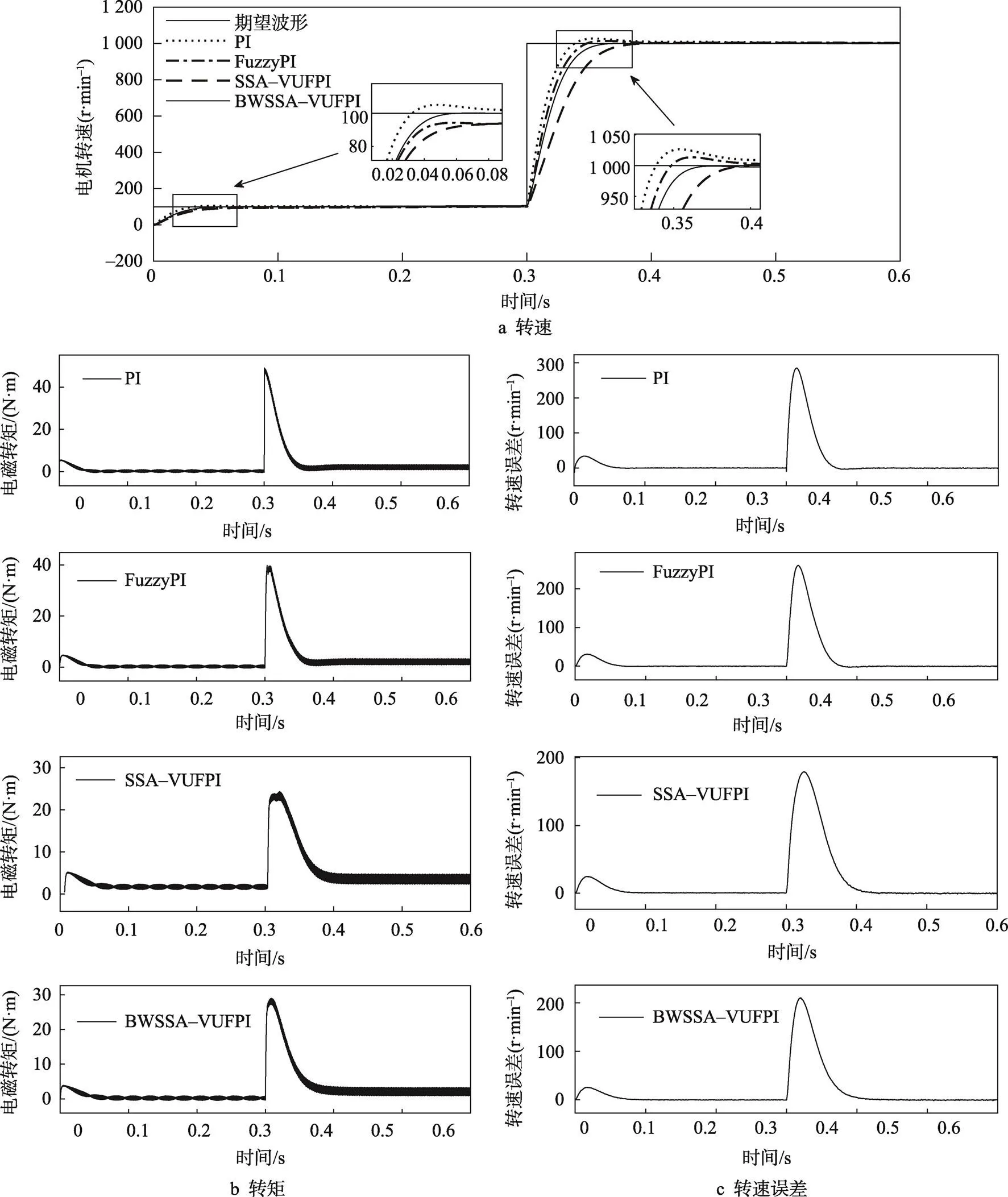
图6 空载变速实验仿真波形图
表4 负载变载实验电机性能指标

Tab.4 Motor performance index under variable load

图7 恒速变载实验仿真波形
5 结语
文中首先将SSA算法进行了合理的优化,并与原算法进行寻优比对,得到了在全局或局部寻优上都更具有优越性的BWSSA算法。然后将BWSSA算法与变论域模糊PI控制器相结合,用于优化变论域中的伸缩因子参数,并运用于PMSM的无传感器控制上。根据空载变速和负载变载实验仿真数据可以得出,使用BWSSA优化的VUFPI控制器可以加快系统的响应速度,且在面临外界干扰时也会有很强的调节能力,增强控制系统的鲁棒性,不仅提升了控制性能,还有利于无传感器控制下的观测器对转速的跟进。
[1] 温盛军, 梁彤伟, 王佩雪. 基于位置估计的永磁同步电机全速域控制[J]. 南京理工大学学报, 2020, 44(1): 80-86.
WEN Sheng-jun, LIANG Tong-wei, WANG Pei-xue. Position Estimation Based Sensorless Control for Permanent Magnet Synchronous Motor in Full Speed Range[J]. Journal of Nanjing University of Science and Technology, 2020, 44(1): 80-86.
[2] 高靖凯, 林荣文, 张润波. 永磁同步电机直接转矩控制的研究及算法改进[J]. 电机与控制应用, 2015, 42(11): 16-20.
GAO Jing-kai, LIN Rong-wen, ZHANG Run-bo. Research and Algorithm Improvement of Permanent Magnet Synchronous Motor Direct Torque Control[J]. Electric Machines & Control Application, 2015, 42(11): 16-20.
[3] 张巍, 刘跟平, 欧胜. 永磁同步电机前馈补偿和单神经元PID控制[J]. 电气传动, 2016, 46(12): 12-15.
ZHANG Wei, LIU Gen-ping, OU Sheng. Permanent Magnet Synchronous Motor Control System Based on Feed-Forward Compensation and Single Neuron PID[J]. Electric Drive, 2016, 46(12): 12-15.
[4] 王福杰. 基于模糊PID控制和BP神经网络PID控制的永磁同步电机调速方案比较研究[J]. 微电机, 2020, 53(6): 103-107.
WANG Fu-jie. A Comparative Study of Speed Control Schemes of PMSM Based on Fuzzy PID Control and BP Neural Network PID Control[J]. Micromotors, 2020, 53(6): 103-107.
[5] 李洪兴. 变论域自适应模糊控制器[J]. 中国科学E辑(技术科学), 1999, 29(1): 32-42.
LI Hong-xing. Variable Universe Adaptive Fuzzy Controller[J]. Science in China, SerE, 1999, 29(1): 32-42.
[6] MIRJALILI S, GANDOMI A H, MIRJALILI S Z, et al. Salp Swarm Algorithm: A Bio-Inspired Optimizer for Engineering Design Problems[J]. Advances in Engineering Software, 2017, 114: 163-191.
[7] 范千, 陈振健, 夏樟华. 一种基于折射反向学习机制与自适应控制因子的改进樽海鞘群算法[J]. 哈尔滨工业大学学报, 2020, 52(10): 183-191.
FAN Qian, CHEN Zhen-jian, XIA Zhang-hua. A Modified Salp Swarm Algorithm Based on Refracted Opposition-Based Learning Mechanism and Adaptive Control Factor[J]. Journal of Harbin Institute of Technology, 2020, 52(10): 183-191.
[8] 陈忠云, 张达敏, 辛梓芸. 多子群的共生非均匀高斯变异樽海鞘群算法[J]. 自动化学报, 2022, 48(5): 1307-1317.
CHEN Zhong-yun, ZHANG Da-min, XIN Zi-yun. Multi-Subpopulation Based Symbiosis and Non-Uniform Gaussian Mutation Salp Swarm Algorithm[J]. Acta Automatica Sinica, 2022, 48(5): 1307-1317.
[9] 刘景森, 袁蒙蒙, 李煜. 基于改进樽海鞘群算法求解工程优化设计问题[J]. 系统仿真学报, 2021, 33(4): 854-866.
LIU Jing-sen, YUAN Meng-meng, LI Yu. Solving Engineering Optimization Design Problems Based on Improved Salp Swarm Algorithm[J]. Journal of System Simulation, 2021, 33(4): 854-866.
[10] 王梦秋, 王艳, 纪志成. 基于改进樽海鞘群算法的PMSM多参数辨识[J]. 系统仿真学报, 2018, 30(11): 4284-4291.
WANG Meng-qiu, WANG Yan, JI Zhi-cheng. Permanent Magnet Synchronous Motor Multi-Parameter Identification Based on Improved Salp Swarm Algorithm[J]. Journal of System Simulation, 2018, 30(11): 4284-4291.
[11] 时维国, 刘坤亮. 改进型高频方波注入的PMSM无传感器控制算法[J]. 微电机, 2018, 51(6): 40-45.
SHI Wei-guo, LIU Kun-liang. Research on PMSM Sensorless Control of Improved High Frequency Square Wave Injection[J]. Micromotors, 2018, 51(6): 40-45.
[12] LIU J M, ZHU Z Q. Sensorless Control Strategy by Square-Waveform High-Frequency Pulsating Signal Injection into Stationary Reference Frame[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2): 171-180.
[13] 王霞, 朱景伟. 基于模糊PI控制的无刷直流电机调速系统[J]. 电气传动, 2014, 44(1): 63-67.
WANG Xia, ZHU Jing-wei. Speed Control System of Brushless DC Motor Based on Fuzzy PI Regulator[J]. Electric Drive, 2014, 44(1): 63-67.
[14] 胡顺强, 崔东文. 基于海洋捕食者算法优化的长短期记忆神经网络径流预测[J]. 中国农村水利水电, 2021(2): 78-82.
HU Shun-qiang, CUI Dong-wen. Long-Term and Short-Term Memory Neural Network Runoff Prediction Based on Optimization of Marine Predators Algorithm[J]. China Rural Water and Hydropower, 2021(2): 78-82.
[15] 李代华, 崔东文. 基于PCA–MPA–ANFIS模型的年径流预测研究[J]. 水电能源科学, 2020, 38(7): 24-29.
LI Dai-hua, CUI Dong-wen. Annual Runoff Forecasting Based on PCA-MPA-ANFIS Model[J]. Water Resources and Power, 2020, 38(7): 24-29.
[16] 宁杰琼, 何庆.–分布扰动策略和变异策略的花授粉算法[J]. 小型微型计算机系统, 2021, 42(1): 64-70.
NING Jie-qiong, HE Qing. Flower Pollination Algorithm Based on T-Distribution Perturbation Strategy and Mutation Strategy[J]. Journal of Chinese Computer Systems, 2021, 42(1): 64-70.
[17] SALGOTRA R, SINGH U, SINGH S, et al. Self-Adaptive Salp Swarm Algorithm for Engineering Optimization Problems[J]. Applied Mathematical Modelling, 2021, 89(1): 188-207.
[18] ALJARAH I, HABIB M, FARIS H, et al. A Dynamic Locality Multi-Objective Salp Swarm Algorithm for Feature Selection[J]. Computers & Industrial Engineering, 2020, 147(1): 147-148
[19] ZHANG Li-ming, WANG Sai-sai, ZHANG Kai, et al. Cooperative Artificial Bee Colony Algorithm with Multiple Populations for Interval Multiobjective Optimization Problems[J]. IEEE Trans Fuzzy Systems, 2019, 27(5): 1052-1065.
[20] 余江, 杨世春, 李亚伦. 永磁同步电机矢量控制系统建模仿真研究[J]. 计算机仿真, 2019, 36(3): 179-183.
YU Jiang, YANG Shi-chun, LI Ya-lun. Research on Modeling and Simulation of Vector Control System for Permanent Magnet Synchronous Motor[J]. Computer Simulation, 2019, 36(3): 179-183.
Variable Universe Fuzzy Control of PMSM Based on Improved SSA
JIN Ai-juan, FENG Ya-ru, LI Shao-long
(University of Shanghai for Science and Technology, Shanghai 200093, China)
The work aims to propose a new variable universe fuzzy controller based on improved salp swarm algorithm to solve the problems of large steady-state error and poor anti-interference caused by the non-timely adjustment of PI controller parameters of permanent magnet synchronous motor, to improve the production efficiency of automatic packaging line. Through the migration strategy and variation distribution strategy, the position update of salp swarm intelligent algorithm was improved, and the weighted position correction of the crossing individuals and the secondary migration of the inferior individuals were introduced. The optimized algorithm was combined with variable universe fuzzy PI controller to adjust the contraction-expansion factor, so as to achieve better control effect of permanent magnet synchronous motor. The simulation results showed that the optimized controller had smaller offset than the traditional PI controller; meanwhile, it made PMSM respond faster in working conditions of variable speed and load. Compared with that before improvement, the overshoot of PI controller based on SSA was decreased by 21.35% and 62.85% respectively. Compared with other control, the variable universe fuzzy control obtained by the algorithm after optimizing the contraction-expansion factor can improve the robustness of the system more effectively, improve the control performance of the system, and reduce the loss in the process of variable speed.
Permanent Magnet Synchronous Machines; Variable Universe Fuzzy control; Salp Swarm Algorithm; contraction-expansion factor
TB486
A
1001-3563(2022)13-0264-11
10.19554/j.cnki.1001-3563.2022.13.034
2021‒09‒10
国家自然科学基金(11502145)
金爱娟(1972—),女,博士,上海理工大学副教授,主要研究方向为控制理论、电机控制和电力电子。
责任编辑:曾钰婵
