阀口袋套袋机器人轨迹优化方法研究

李雪梅，崔菲菲，郭义华，张鑫，容北国

阀口袋套袋机器人轨迹优化方法研究

李雪梅1，崔菲菲1，郭义华1，张鑫1，容北国2

（1.桂林电子科技大学 机电工程学院，广西 桂林 541004； 2.桂林鸿程矿山设备制造有限责任公司，广西 桂林 541199）

为了提高阀口袋套袋机器人的工作效率，提出基于改进粒子群算法的阀口袋套袋机器人时间最优轨迹规划方法。首先，通过逆运动学方程反解出操作空间轨迹对应的关节空间角度值。其次，采用4–3–4混合多项式对阀口袋套袋机器人的关节空间轨迹进行插值拟合。最后，在速度约束条件下，利用改进粒子群算法对阀口袋套袋机器人的运行时间进行优化处理。仿真结果表明，改进粒子群算法可以在保证阀口袋套袋机器人运行平稳的条件下将总运行时间缩减41.66%，实现了阀口袋套袋机器人在关节空间中时间最优的轨迹规划。该方法可有效地提高机器人工作效率，延长机器人的使用寿命，为阀口袋套袋机器人稳定可靠运行提供了科学依据。

阀口袋套袋机器人；时间最优；轨迹规划；混合多项式；改进粒子群算法

近几年来，机器人技术在粉体包装行业得到了大范围的应用[1]，企业对工业机器人的生产效率也提出了更高的要求[2]，仅实现机器人平稳、光滑的运行轨迹已不能满足实际生产要求[3]。阀口袋[4]套袋机器人操作对象是粉体，其操作对象细小易散，如果轨迹规划不合理极易导致被包装物体散落，因此文中针对包装行业中阀口袋套袋机器人经过多个路径点的时间最优轨迹规划技术展开研究。

在机器人轨迹规划中，针对时间最优这一目标，当前国内外专家学者使用较多的方法是遗传算法[5-7]。粒子群算法还需要更深入的研究和讨论，但目前也有一定的研究基础[8]。粒子群算法相对于遗传算法的优点是，它没有遗传算法的“交叉”和“变异”操作，是通过追随当前搜索到的最优值来寻找全局最优[9]。韩顺杰等[10]针对传统工业机器人轨迹规划效率低等问题，提出了可以动态调节学习因子的粒子群算法。王延年等[11]在B样条轨迹规划的基础上，结合改进粒子群优化算法，对整条运行路径进行时间优化，最终达到了较好的优化结果。Ma等[12]采用遗传算法对机器人的时间最优轨迹进行规划，该算法的缺点是容易早熟。文中在4–3–4混合多项式[13]插值函数的基础上，采用改进粒子群算法进行优化，该方法参数可调，可有效避免标准粒子群算法容易陷入局部最优解的问题。

文中将4–3–4混合多项式和粒子群算法相结合的方法对阀口袋套袋机器人的运行轨迹进行时间优化，仿真结果表明该方法可以缩短阀口袋套袋机器人关节空间运动的时间，缩短41.66%，整体上可以提高阀口袋套袋机器人的工作效率。

1 阀口袋套袋机器人运动学分析

对阀口袋套袋机器人的关节空间进行轨迹规划，首先需要知道笛卡尔空间[14]中位置点对应关节空间[15]中的角度值，因此，对阀口袋套袋机器人进行正逆运动学求解是研究阀口袋套袋机器人轨迹规划的基础。文中研究的阀口袋套袋机器人三维模型见图1，其运行路径包括7个关键节点，分别是起始点、下降点、定位点、取袋点、夹紧点、开袋点以及套袋点。阀口袋套袋机器人的工作示意图见图2，根据机器人的结构模型对其建立连杆坐标系见图3。

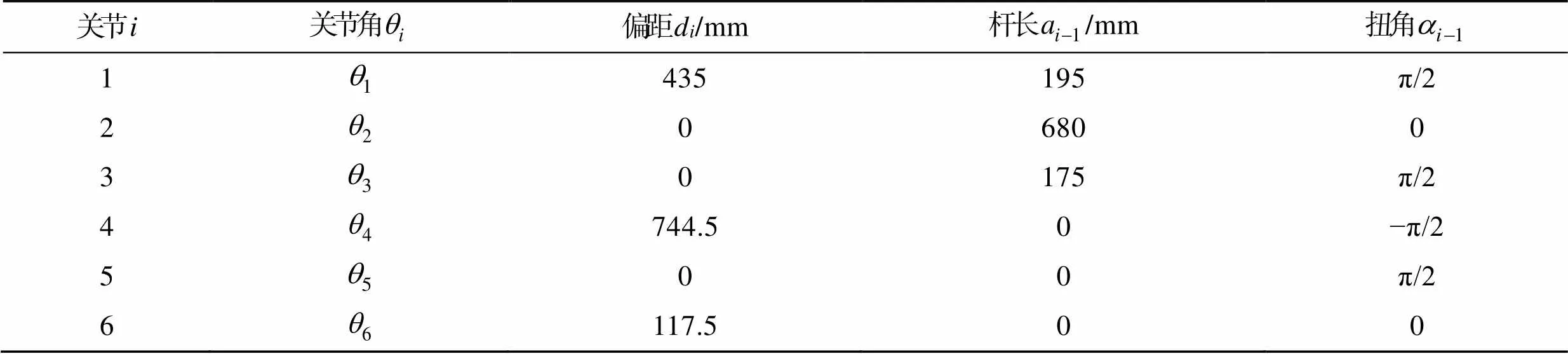
根据机器人的坐标系可推导出其D–H参数[16]，见表1。

1.1 正运动学分析

根据齐次变换矩阵可以计算出阀口袋套袋机器人末端执行器与基座之间的总变换矩阵：

(1)

图1 阀口袋套袋机器人三维模型

Fig.1 3D-model of valve pocket bagging robot

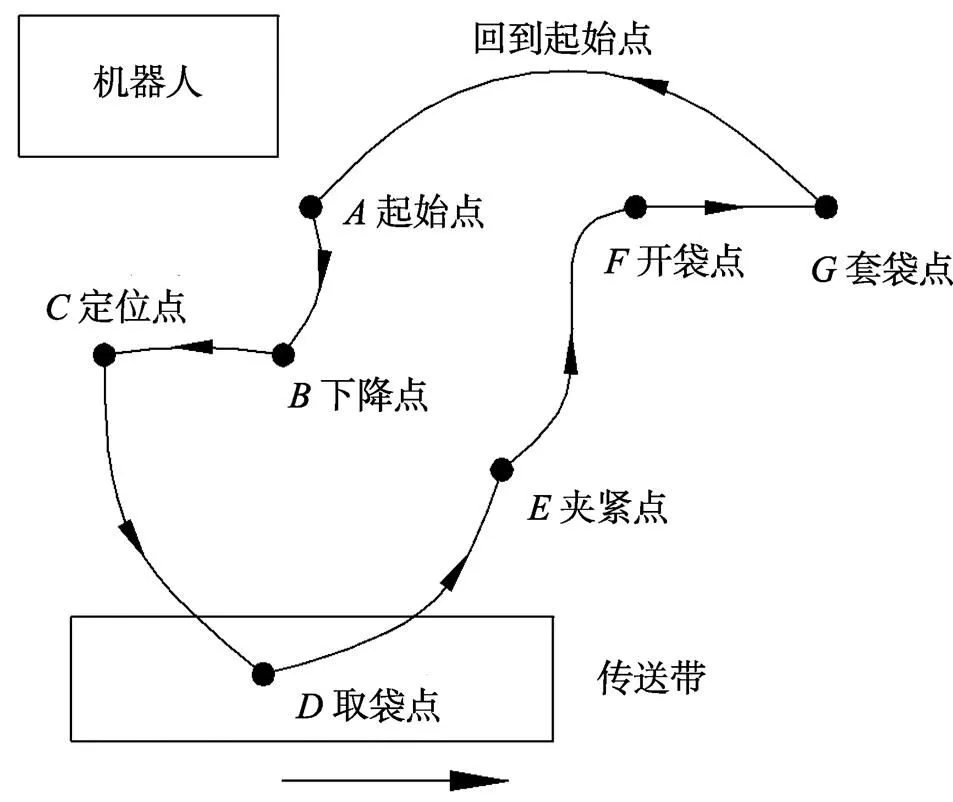
图2 阀口袋套袋机器人工作示意图

图3 阀口袋套袋机器人的D–H坐标系

表1 阀口袋套袋机器人的D–H参数

Tab.1 D-H parameters of valve pocket bagging robot

式中：n=sin6sin1cos4sin6cos1sin4·cos (2+3)−cos6cos1sin5sin(θ+θ)+cos6·cos5sin1sin4+cos6cos5cos4cos1cos(2+3)；n=−sin6cos1cos4sin6sin1sin4cos(θ+θ)−cos6sin1sin5sin(2+3)−cos6cos5cos1·sin4+cos6cos5cos4sin1cos(2+3)；n=cos6·sin5cos(2+3)+cos6cos4cos5sin(2+3)−sin4·sin6sin(2+3)；O=sin6cos1sin5sin(2+3)sin65sin1sin4−sin6cos5cos1·cos4cos(2+3)+cos6sin1cos4−cos6sin4·cos1cos(2+3)；O=sin6sin1sin5sin(2+3)+·sin6cos5cos1sin4−sin6sin1cos5·cos4cos(θ+θ)−cos6cos1co s4−cos6sin4·sin1cos(2+3)；O=−cos6sin4·sin(θ+θ)−sin6·sin5cos(θ+θ)−cos4cos5·sin6sin(θ+θ)；a=·cos1cos5sin(2+3)+sin1·sin5sin4cos1sin5·cos4cos(2+3)；a=sin1·cos5sin(θ+θ)−cos1·sin5sin4sin1sin5cos4·cos (θ+θ)；a=cos4·sin5sin(2+3)−cos5cos(2+3)；p=a1cos1+4·cos1sin(2+3)+2cos1cos23·cos1cos(θ+θ)+6cos1cos5sin(2+3)+6sin1·sin5sin4+6cos1sin5cos4cos(2+3)；p=a1·sin1+4sin1sin(2+3)+2sin1cos23·sin1·cos(2+3)+6·sin1cos5sin(2+3)−6sin5cos1·sin4+6sin1·sin5cos4cos(θ+θ)；p=d1+2·sin24cos(2+3)+3·sin (2+3)−6cos5cos(2+3)+6·sin5cos4sin(2+3)。

1.2 逆运动学分析

由于文中研究的阀口袋套袋机器人的关节4、5、6的轴线相交于一点，满足Piper准则[17]，因此采用反变换法求解6个关节角度值。求解出的6个关节角度分别如下。

关节角1：

或

(2)

关节角2：

(3)

式中：1(6a−p)sin1+(6a−p)cos1，n=p−6a−6，。

关节角3：

3=tan2(sin3,cos3) (4)

式中：

关节角4：

(5)

式中：

关节角5：

(6)

式中：

关节角6：

6=tan2(sin6, cos6) (7)

式中：

2 阀口袋套袋机器人轨迹规划

2.1 阀口袋套袋机器人关键节点处关节角度值

如图4所示，阀口袋套袋机器人的运行路径中包含7个关键节点。点是阀口袋套袋机器人的初始点；点是阀口袋套袋机器人的下降点，目的是避免阀口袋套袋机器人在运行过程中碰撞到相机；点是定位点，相机将拍照结果传给阀口袋套袋机器人；点为取袋点，阀口袋套袋机器人根据相机拍摄的结果去拾取袋子；点为夹紧点，将吸取到的袋子夹紧，防止运行过程中袋子掉落；点为开袋点，末端执行器将袋子的阀口吸开，为了下一步袋子能够套在出料口上；点为套袋点，将吸开的阀口袋套在出料口上，向袋子中填充粉体。然后阀口袋套袋机器人再回到初始点如此循环往复即可达到阀口袋套袋生产要求。

将阀口袋套袋机器人末端点的坐标代入到逆解中，求解出阀口袋套袋机器人在7个位置处的6个关节角度值，见表2。

2.2 4–3–4混合多项式轨迹规划

采用4–3–4混合多项式插值方法对阀口袋套袋机器人的关节空间进行插值。由于阀口袋套袋机器人的路径中含有7个关键节点，因此共含有6段运行轨迹，其中第1段和最后1段轨迹采用4次多项式进行拟合，中间的4段轨迹采用3次多项式进行拟合，拟合得到的各段轨迹的位置、速度和加速度函数表达式见式（8）。

图4 阀口袋套袋机器人运动路径关键节点位置

(8)

根据关键节点处位移速度以及加速度相等的条件，可以得到阀口袋套袋机器人的系数表达式：

(9)

式中：

表2 关键节点处关节角度值

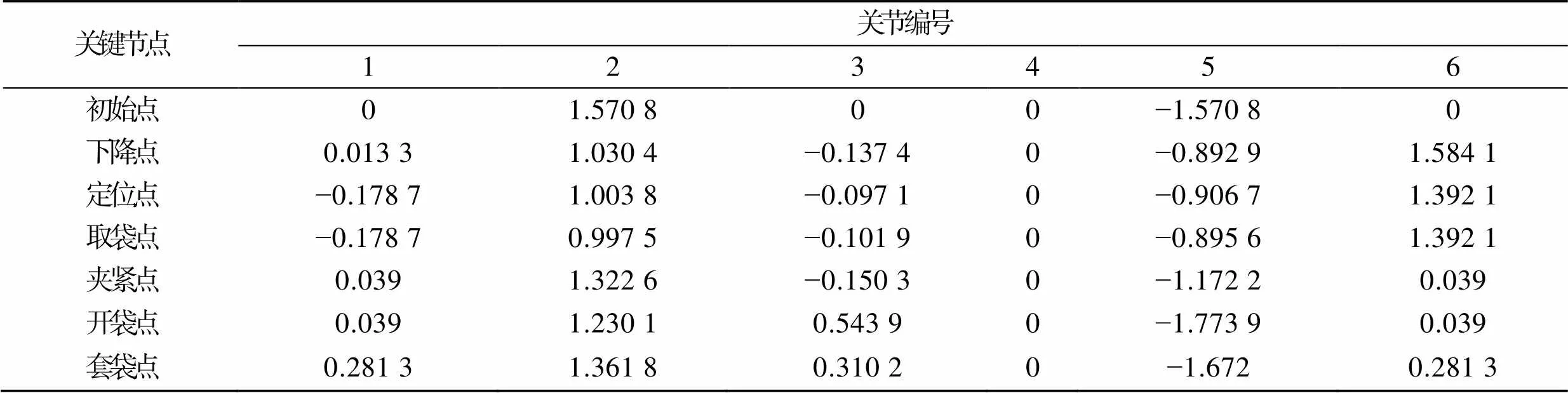
Tab.2 Joint angle values at key nodes rad

3 改进粒子群的时间最优轨迹

根据式（8）可知，混合多项式中的时间与系数是相关联的。求解出混合多项式的系数的前提条件是先求解出每段轨迹的运行时间，因此在对机器人的运行时间优化之前，需要在满足速度约束的条件下得到每段轨迹的最优时间。

文中研究的阀口袋套袋机器人在实际生产过程中要完成从取袋→开袋→套袋等一系列动作，需要经过轨迹中指定的7个关键节点1～7，7个关键节点对应的时间分别为1～7。关键节点之间的时间间隔为Δt，Δt=t+1−t（=1,2,…,6），则机器人一个工作周期的总运行时间总（即优化目标函数）表示为：

(10)

速度约束条件表达式为：

(11)

式中：为阀口袋套袋机器人关节数，=1,…,6；为阀口袋套袋机器人运行轨迹段数，=1,…,6。

由于混合多项式插值方法不具有优化的性质，因此文中采用改进粒子群算法对时间进行优化。假设一个由个粒子组成的种群在维的搜索空间以一定的速度飞行。粒子在时刻的位置向量为，速度向量为，个体最优位置为p，全局最优位置g。

则粒子在+1时刻的位置通过下式更新获得：

(12)

(13)

(14)

式（12）中线性学习（加速）因子1、2的计算式见式（15）—（16）。

(15)

(16)

式中：1s2s为迭代开始时的加速因子，1s2s0.05；1e2e为迭代结束时的加速因子，1e2e0.02。

基于改进粒子群算法对第个关节轨迹规划的实现步骤如下。

1）第个关节的6个时间段中分别随机产生个粒子，则每段中将会有个粒子组成的种群，一共有6个种群。种群的大小为（一般设定在20～50），文中设定为20。

2）初始化种群的速度和位置，并从当前个体极值中寻找全局极值。

3）设置粒子的长度（即自变量的数量），文中有6个自变量，则=6。

4）将产生的组混合多项式插值时间t1～t6代入到第2.2节系数矩阵方程中，求解出6段多项式的系数矩阵。

5）将求解的系数代入到式（8）中求解出6段混合多项式函数，分别对6段混合多项式函数求导得到相应的速度函数，并根据式（11）判断其速度是否超过关节所允许的最大速度。

6）计算每个粒子的适应度值，筛选步骤5中的结果。在这6段中，假设其中任何一段存在粒子速度不满足约束条件，则将此粒子的适应度值设置为最大值，然后通过粒子在寻优过程中适者生存的法则，可以将此粒子淘汰掉，进而避免了此粒子成为全局最优粒子。相反，如果这6段中每个粒子速度的最大值均满足速度约束条件，则用式（10）来替换当前适应度函数。

7）评价空间中每个粒子在搜索过程中的适应度值p，并将此值与该粒子的适应度值相比较，若好于当前则留下，否则继承当前的适应度值。

8）对种群中所有粒子的适应度值进行评价，选出当前种群中最优的粒子。假设该粒子的适应度值比当前的g的值好，则用该粒子的适应度值代替掉g，否则将保留历史种群全局最优解。

9）用式（11）和式（12）对每个粒子的速度和位置进行更新，重新生成新的由个粒子构成的种群。

10）判断是否满足结束条件。满足则结束，否则跳到步骤4，如此循环往复。

在同一段轨迹中对6个关节的运行时间进行比较，筛选出耗时最长的关节，并将此关节的时间设定为该段轨迹的运行时间。最后，将每段轨迹的时间相加，所得到时间即为机器人运行完整段轨迹的时间，进而可得到阀口袋套袋机器人最终的优化轨迹函数。

4 实验验证

由于目前实验室阀口袋套袋机器人理论上1 min可以上袋5～6个，所以计算出阀口袋套袋机器人每个运行周期为10～12 s。为了能充分利用阀口袋套袋机器人的工作性能，文中采用混合多项式插值法对每个关节进行轨迹规划，每段规划时间无确定的准则。在满足各个关节位置、速度、最大速度不超过其最大限定值条件下，设定每段轨迹的插值时间为2 s。机器人在起始与终点处的速度、加速度均为0。

4.1 仿真验证

在对阀口袋套袋机器人各关节添加速度约束条件后，基于4–3–4混合多项式插值方法在Matlab软件中编写改进粒子群代码，可求解出阀口袋套袋机器人的5个关节最优时间。

由表2可知，阀口袋套袋机器人的第4个关节在整个运行过程中没有参与运动，因此只需对其余5个关节进行优化，通过仿真可得到5个关节最优粒子位置进化与迭代次数的关系，见图5。

经过改进粒子群算法的200次迭代后可以得到6个关节在各个段的插值时间，其结果见表3。

由表3可以看出，优化后的整条轨迹的运行时间为7.000 5 s，比优化前减少了4.999 5 s，运行时间缩短了41.66%。在4–3–4多项式插值函数基础上，经过改进粒子群优化之后的阀口袋套袋机器人的角位移、角速度以及角加速度曲线见图6。

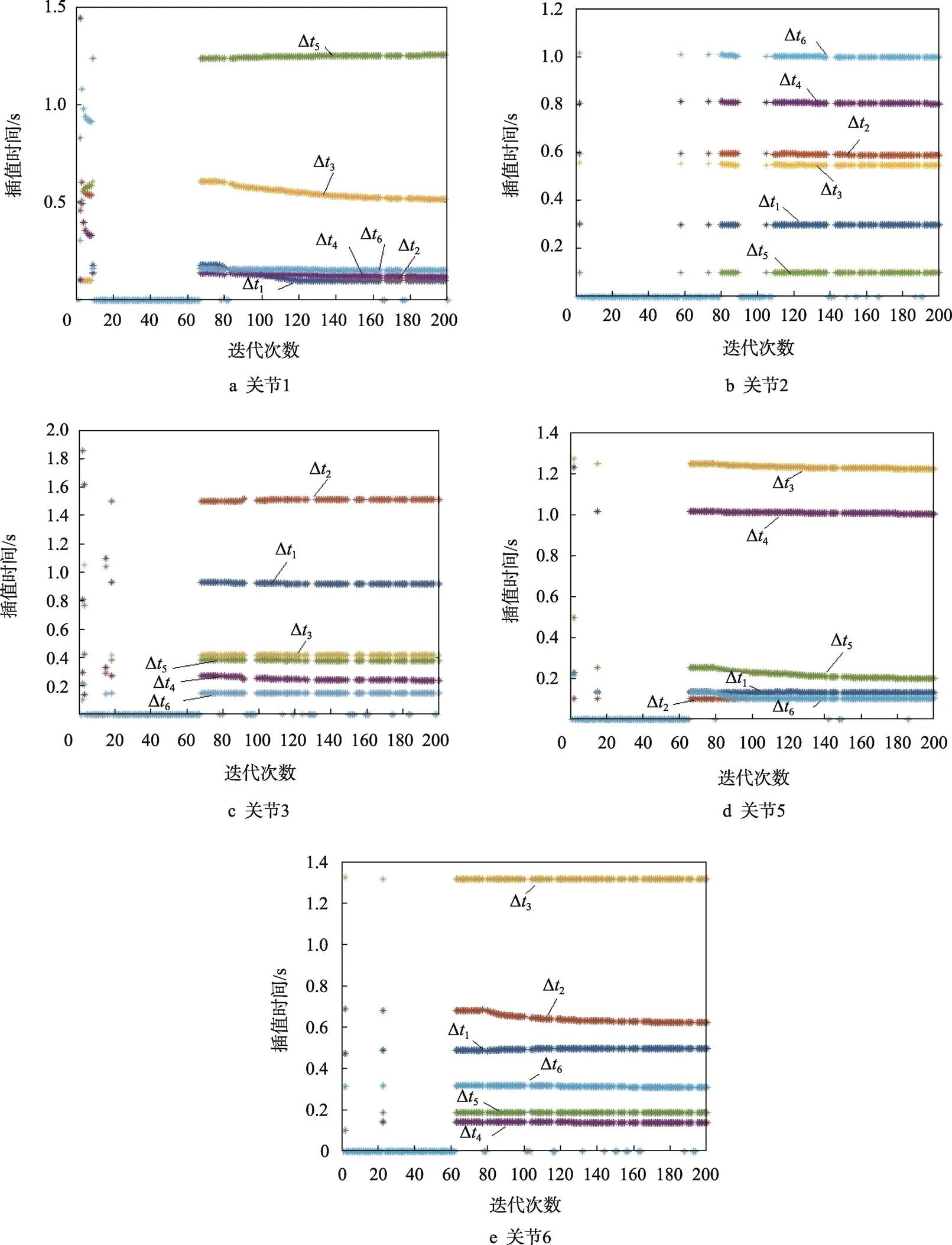
图5 关节粒子位置进化

表3 改进粒子群算法的优化结果

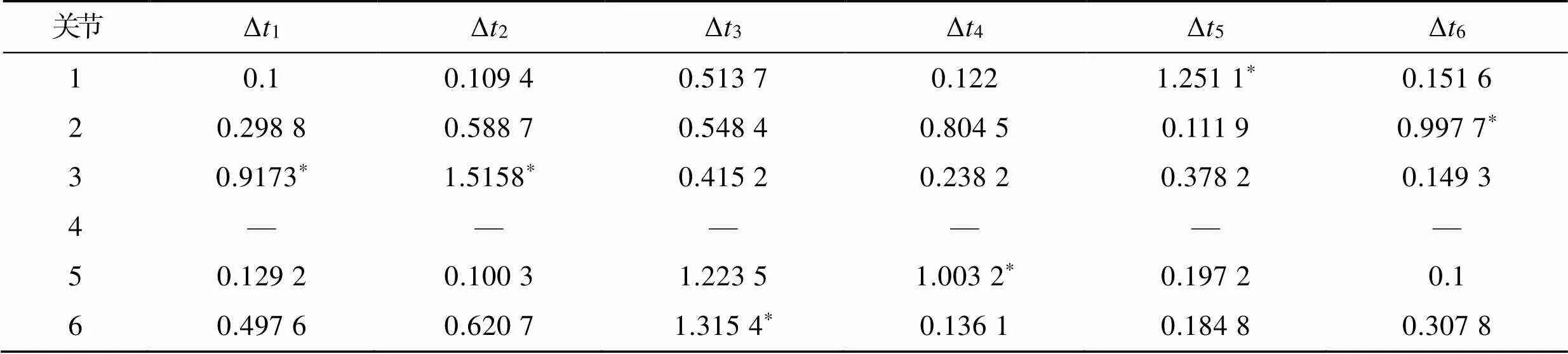
Tab.3 Optimization results of improved particle swarm optimization algorithm s

注：*代表每列中的最大值。

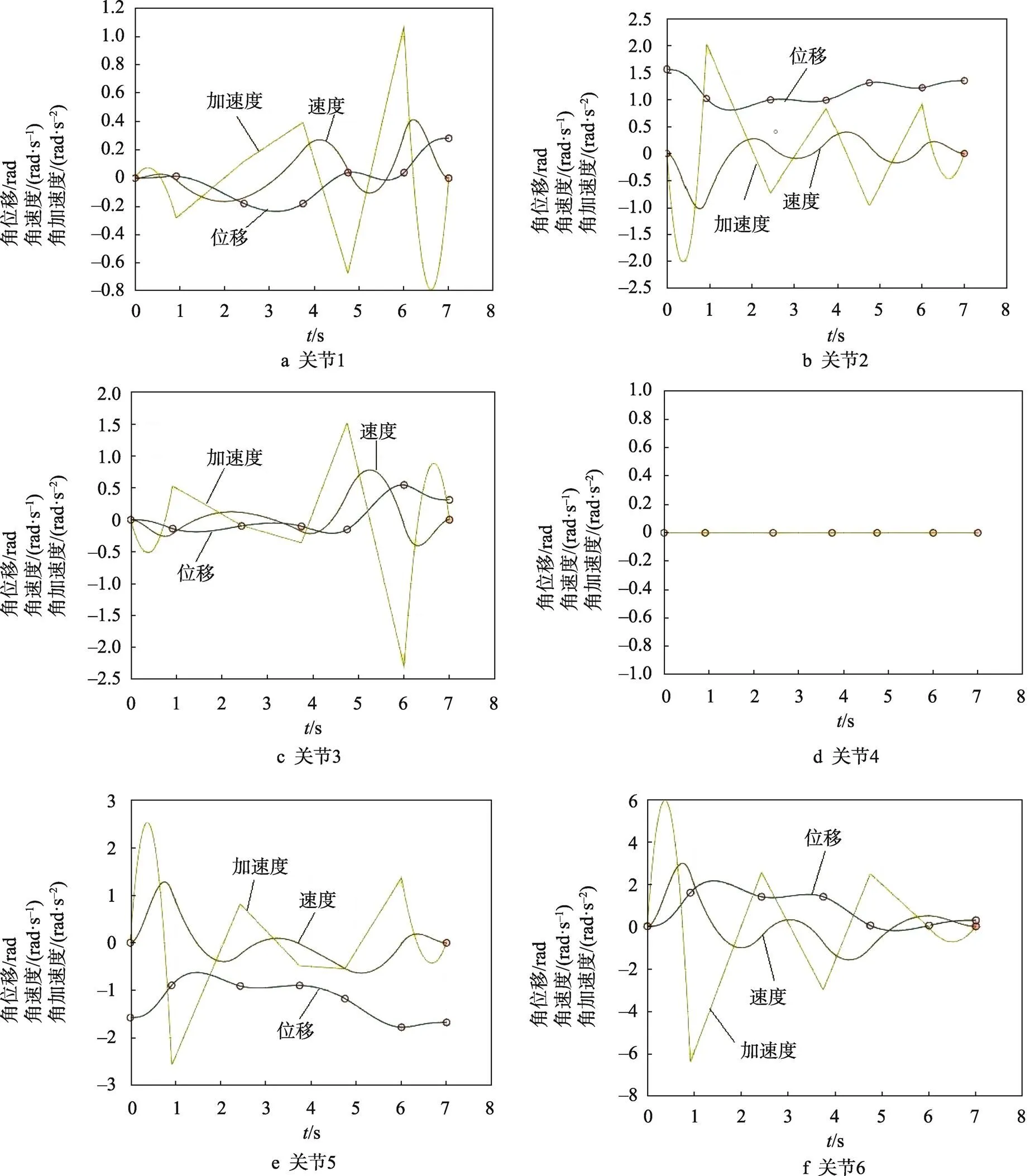
图6 粒子群优化的机器人各关节曲线

由图6中可以看出，优化后的各个关节角位移、角速度和角加速度曲线连续且加速度值较小，速度和加速度在整条曲线上都是从0逐渐增加或者逐渐减小到0，在保证轨迹连续的条件下，保证了阀口袋套袋机器人的平稳运行。

4.2 实验验证

采用实验室阀口袋套袋机器人进行实际验证，传送带将阀口袋运送到视觉有效视场范围内，通过机器视觉识别到的阀口袋的三维坐标发送给工控机。根据机器人初始点和终止点的坐标，用混合多项式算法得到机器人各个关节旋转角度随时间变化的序列，将得到的数值发送给机器人，机器人按照控制器生成的轨迹运动，如此往复循环完成生产要求。阀口袋套袋机器人抓取袋子、夹紧袋子、开袋以及套袋的运动过程见图7，利用文中的时间优化算法可以精确地完成整个套袋任务。

图7 阀口袋套袋机器人运动过程

5 结语

在4–3–4混合多项式的基础上，利用改进粒子群算法对阀口袋套袋机器人运行轨迹进行优化，该算法相对高阶多项式其具有计算简便的优点，得到了时间最优的轨迹规划算法。根据Matlab仿真图和阀口袋套袋机器人实验验证可以得出，优化后的轨迹角位移、角速度和角加速度连续，且角加速度值较小。在运动速度约束条件下，采用改进粒子群算法可使机阀口袋的运行时间由原来的12 s缩短到7.000 5 s，提高了阀口袋套袋机器人的工作效率，从而证明了改进粒子群算法的可行性。

[1] 李远, 农秉茂. 包装搬运机器人运动轨迹优化设计[J]. 包装工程, 2020, 41(1): 123-127.

LI Yuan, NONG Bing-mao. Optimization Design of Moving Trajectory for Packaging Handling Robot[J]. Packaging Engineering, 2020, 41(1): 123-127.

[2] 陈义时, 吴湘柠, 周立, 等. 全自动包装码垛机器人生产线系统设计[J]. 装备制造技术, 2019(6): 26-28.

CHEN Yi-shi, WU Xiang-ning, ZHOU Li, et al. Design of Automatic Packing and Palletizing Robot Line System[J]. Equipment Manufacturing Technology, 2019(6): 26-28.

[3] 党宏社, 张梦腾, 候金良, 等. 工业装配机器人轨迹规划算法研究[J]. 现代电子技术, 2019, 42(8): 63-67.

DANG Hong-she, ZHANG Meng-teng, HOU Jin-liang, et al. Research on Trajectory Planning Algorithms for Industrial Assembly Robots[J]. Modern Electronics Technique, 2019, 42(8): 63-67.

[4] 王仁龙. 一种阀口袋[J]. 塑料包装, 2020, 30(2): 59-61.

WANG Ren-long. Valve Pocket[J]. Plastics Packaging, 2020, 30(2): 59-61.

[5] 冯斌, 刘峰, 郑飂默. 基于粒子群算法的机器人关节空间最优运动轨迹规划[J]. 组合机床与自动化加工技术, 2018(5): 1-4.

FENG Bin, LIU Feng, ZHENG Liao-mo. Optimal Motion Trajectory Planning of Robot Joint Space Based on Particle Swarm Optimization[J]. Modular Machine Tool & Automatic Manufacturing Technique, 2018(5): 1-4.

[6] 张霞, 孙强, 蔡顺燕, 等. 机器人轨迹规划控制策略研究[J]. 微电机, 2019, 52(11): 76-81.

ZHANG Xia, SUN Qiang, CAI Shun-yan, et al. Research on Robot Trajectory Planning Control Strategy[J]. Micromotors, 2019, 52(11): 76-81.

[7] 杨煜兵, 张春光, 刘光恒, 等. 基于响应面法的柱塞泵迷宫密封优化设计[J]. 流体机械, 2021, 49(6): 44-49.

YANG Yu-bing, ZHANG Chun-guang, LIU Guang-heng, et al. Optimization Design of Labyrinth Seal for Piston Pump Based on Response Surface Method[J]. Fluid Machinery, 2021, 49(6): 44-49.

[8] 王玉宝, 王诗宇, 李备备, 等. 一种改进粒子群的工业机器人时间最优轨迹规划算法[J]. 小型微型计算机系统, 2018, 39(8): 1878-1881.

WANG Yu-bao, WANG Shi-yu, LI Bei-bei, et al. Time Optimal Trajectory Planning Algorithm for Industrial Robots with Improved Particle Swarm Optimization[J]. Journal of Chinese Computer Systems, 2018, 39(8): 1878-1881.

[9] 田恒, 王宗省, 冯叶磊, 等. 一种关节型机器人快速收敛的粒子群优化算法[J]. 机床与液压, 2020, 48(21): 41-44.

TIAN Heng, WANG Zong-sheng, FENG Ye-lei, et al. A Fast Convergent Particle Swarm Optimization Algorithm for Articulated Robots[J]. Machine Tool & Hydraulics, 2020, 48(21): 41-44.

[10] 韩顺杰, 单新超, 于爱君, 等. 基于改进粒子群算法的工业机器人轨迹规划[J]. 制造技术与机床, 2021(4): 9-14.

HAN Shun-jie, SHAN Xin-chao, YU Ai-jun, et al. Industrial Robot Trajectory Planning Based on Improved PSO Algorithm[J]. Manufacturing Technology & Machine Tool, 2021(4): 9-14.

[11] 王延年, 向秋丽. 基于改进粒子群优化算法的六自由度机器人轨迹优化算法[J]. 国外电子测量技术, 2020, 39(1): 49-53.

WANG Yan-nian, XIANG Qiu-li. Trajectory of 6-DOF Robot Based on Improved Particle Swarm Optimization Algorithm[J]. Foreign Electronic Measurement Technology, 2020, 39(1): 49-53.

[12] MA Jian-qi, SHAO Wei-yuan, YE Hao, et al. Arbitrary-Oriented Scene Text Detection via Rotation Proposals[J]. IEEE Transactions on Multimedia, 2018, 20(11): 3111-3122.

[13] GAO M, DING P, YANG Y. Time-Optimal Trajectory Planning of Industrail Robots Based on Particle Swarm Optimization[C]// Fifth International Conference on Instrumention and Measurement, Computer, Communication and Control, IEEE, 2016:1934-1939.

[14] 郭领. 一种串联机器人笛卡尔空间轨迹规划方法[J]. 机械设计与制造工程, 2020, 49(10): 34-40.

GUO Ling. Cartesian Space Trajectory Planning Method for Serial Robot[J]. Machine Design and Manufacturing Engineering, 2020, 49(10): 34-40.

[15] 何康佳, 何玲, 冯磊, 等. 六轴机器人的运动学建模与轨迹规划研究[J]. 机床与液压, 2020, 48(12): 171-176.

HE Kang-jia, HE Ling, FENG Lei, et al. Kinematical Modeling and Trajectory Planning of Six-Axis Robot[J]. Machine Tool & Hydraulics, 2020, 48(12): 171-176.

[16] 冯树先, 刘益剑, 夏慧强, 等. 焊接机器人轨迹规划与运动仿真方法[J]. 制造技术与机床, 2020(11): 61-65.

FENG Shu-xian, LIU Yi-jian, XIA Hui-qiang, et al. Trajectory Planning and Motion Simulation of Welding Robot[J]. Manufacturing Technology & Machine Tool, 2020(11): 61-65.

[17] 赵荣波, 施智平, 关永, 等. 基于旋量理论和代数消元6R机器人逆解算法[J]. 传感器与微系统, 2018, 37(12): 114-117.

ZHAO Rong-bo, SHI Zhi-ping, GUAN Yong, et al. Inverse Kinematic Solution Algorithm of 6R Robots Based on Screw Theory and Algebraic Elimination[J]. Transducer and Microsystem Technologies, 2018, 37(12): 114-117.

Trajectory Optimization Method of Valve Pocket Bagging Robot

LI Xue-mei1, CUI Fei-fei1, GUO Yi-hua1, ZHANG Xin1, RONG Bei-guo2

(1. School of Mechanical and Electrical Engineering, Guilin University of Electronic Technology, Guangxi Guilin 541004, China; 2. Guilin Hongcheng Mining Equipment Manufacturing Co., Ltd., Guangxi Guilin 541199, China)

The work aims to propose a time-optimal trajectory planning method for the valve pocket bagging robot based on improved particle swarm optimization algorithm, so as to improve the working efficiency of the robot. Firstly, the joint space angle corresponding to the trajectory of the operating space was solved by the inverse kinematics equation. Then, the joint space trajectory was fitted by 4-3-4 mixed polynomial interpolation method. Finally, the improved particle swarm optimization algorithm was used to optimize the running time of the valve pocket bagging robot under the speed constraints. From the simulation results, the improved particle swarm optimization algorithm could reduce the total running time by 41.66% under the condition of ensuring the smooth running of the valve pocket bagging robot, and realize the time-optimal trajectory planning of the valve pocket bagging robot in joint space. The method can effectively improve the working efficiency of the robot, prolong the service life of the robot, and provide a scientific basis for the stable and reliable operation of the valve pocket bagging robot.

valve pocket bagging robot; time-optimal; trajectory planning; mixed polynomial; MPSO

TP242

A

1001-3563(2022)13-0180-09

10.19554/j.cnki.1001-3563.2022.13.023

2021‒08‒16

广西科技攻关计划（2017AA24007）；广西研究生教育创新计划（YCSW2018135）

李雪梅（1971—），女，硕士，桂林电子科技大学教授，主要研究方向为机电控制与自动化、数字化设计与特种加工技术。

责任编辑：曾钰婵