非对称压差下三角形微孔摩擦副的两向异性应用

吉 华，张子扬，段宗幸，陈 志

(1.四川大学 化学工程学院，四川 成都 610065；2.西藏农牧学院 水利土木工程学院，西藏 林芝 860000)

在平行的摩擦副表面加工微孔，能够提高液膜承载力，减小摩擦，主要应用于机械密封、推力轴承、滑动轴承、活塞-气缸等机构中。微孔的几何形状和尺寸是影响微孔性能的主要因素，早期的研究主要集中于圆形微孔，近年来，椭圆形、矩形、三角形、V形等规则方向性微孔以及一些非规则形状的微孔也得到了一定的研究。

研究方向性微孔的主要目的是找到在一个确定的方向运动时，微孔的最佳方向角（摆放方向）。Ding等通过实验研究了微孔几何形状（圆形、棱形、矩形和椭圆形）对摩擦系数的影响，结果表明孔型对摩擦性能有显著影响，长轴垂直于滑动方向的椭圆形微孔效果最好。Meng等采用数值计算的方法研究了椭圆形、菱形、三角形和矩形等方向性孔对流量的影响，研究发现，通过调节摆放角度可以控制油膜流量，存在使回流最大的摆放角度，且矩形孔的控制能力最强。Hingawe和Bhore采用了数值计算的方法，研究了具有不同截面轮廓（平板、三角形T1、三角形T2、半圆形）微孔的平行摩擦副的摩擦性能。结果表明，三角形T2底型的摩擦系数最小，承载能力最大；使不同的孔型摩擦性能最优的速度和几何参数并不相同。

Shen和Khonsari采用基于序列二次规划算法的形状优化方法得出结论：在单向滑动和两向滑动时的最佳微孔形状是燕尾形和对称梯形。该研究中在正反向滑动时工况相同。

以上研究都表明，具有不对称结构的方向性孔的性能与滑动方向有着很大的关系，且在某一个方向角下，往往提供比圆形孔更大的承载力，减少摩擦的性能也更为优越。

Lu等在往复摩擦机上对带有三角形微孔的试件展开了线-面接触实验。基于实验结果，他们提出了摩擦系数各向异性的概念，即：不同运动方向的摩擦系数是不同的，原因是线接触长度的差异。他们的实验是开放实验，运动两侧压力均为大气压，即压差为零。

以上研究旨在探寻固定方向运动时的最佳微孔几何参数，没有与实际工况联系起来。往复运动的机构，例如活塞环-缸套、往复运动的滑动轴承等，它们在往做功侧运动时，由于外载荷较大，往往承受较高压力；而在返回时，压力较低。往复运动的研究一般以往复平均参数作为评价指标，反映的是一个往复循环内的平均值，例如平均摩擦系数、平均油膜厚度等。对于具有各向异性的方向性微孔而言，往复平均参数只能最后评价某一确定几何参数微孔的效果，却不能反应出微孔各向异性对工况的适应性，所以这种研究方法不能在设计时给设计者有用的指导信息，不利于微孔几何参数的正向设计和机理理解。

综上，利用非对称表面微织构的各向异性去主动适应不对称工况的研究极为少见。55%的文献采用数值计算的方法研究表面微织构在流体润滑领域的应用。所以，本文采用数值计算的方法，研究带有等边三角形微孔的面-面摩擦副在流体润滑状态时随工况变化的两向运动的性能，利用等边三角形微孔的两向异性特点去适应两向运动中一侧载荷高（压差大）、另一侧载荷低（压差小）的工况特性，以达到一个往复周期内更好地减少摩擦的效果。

1 计算模型

1.1 几何模型

图1为摩擦副几何模型及微孔的示意图。带有微孔的摩擦副如图1（a）所示，其长度为

L

。上滑块有微孔，沿

x

轴两向运动，速度为

u

，下滑块无微孔，且保持静止。微孔深度为

h

，润滑油膜厚为

h

。如图1（c）所示，上平板上均匀分布5个微孔，当上板朝着三角形的尖端方向运动，即运动方向沿

x

轴正方向，将其定义为正向运动，

u

的符号为“+”；反之，

u

的符号为“-”。如图1（b）所示，微孔位于边长为

a

的正方形单元的中心，正三角形微孔边长为

b

。图1（d）中圆形微孔的直径为

d

。

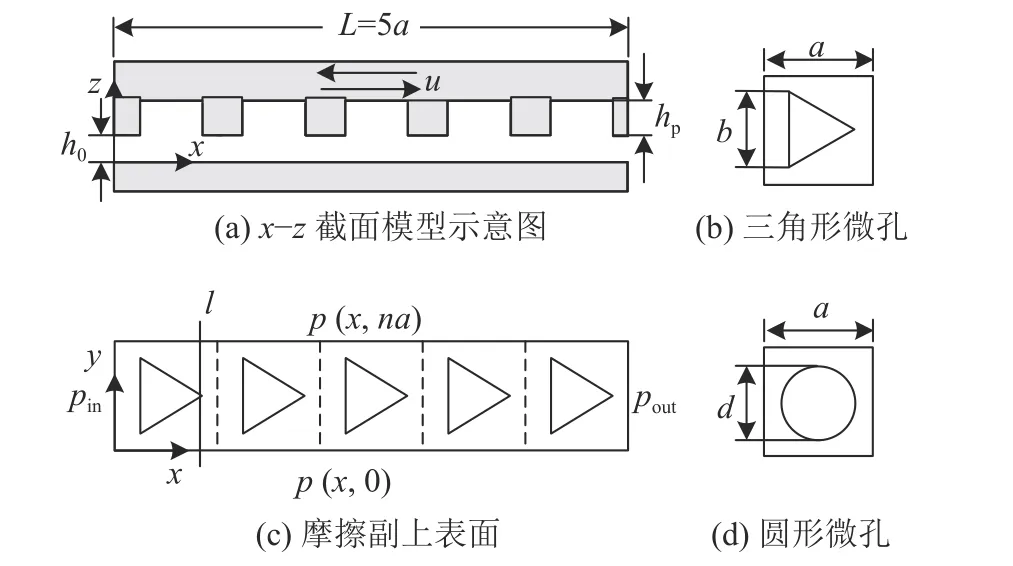
图1 摩擦副几何模型及微孔示意图Fig. 1 Diagram of geometric model of friction pair and micro-dimples

如图1（c）所示，将

y

=0与

y

=

a

处设置为周期性边界，即：

p

(

x

,0)=

p

(

x

,

na

),

n

∈N；正向运动时，

x

=0和

x

=

L

处分别设置为压力进口和压力出口；反向运动时，

x

=0处为压力出口，

x

=

L

处为压力进口；进口压力为

p

，出口压力为

p

；

l

为经过三角形顶点的直线。几何参数如表1所示，其中，微孔面积比

S

定义为：

S

=

S

/

a

。

S

是指开孔面积，在本文中为三角形面积，或者圆形面积（

d

/4）。

表1 几何参数
Tab. 1 Geometric Parameters

参数数值参数数值L/mm2 Sp/%20 a/mm0.4b/μm272 h0/μm3d/μm202 hp/μm3、4、5、6

采用UG软件建立摩擦副间隙流体的3维模型，使用ICEM CFD进行结构性网格划分，采用合并顶点后Y形剖分的方式生成网格，计算模型节点数为1 499 347个，网格质量大于0.85。边界条件及网格划分如图2所示，模型在纸面的法向上具有一定厚度，图2所示的前表面为静壁面，后表面带有微孔，为动壁面。在Fluent软件中进行数值计算，通过后处理软件CFD-Post得到相关数据和云图。计算参数如表2所示。

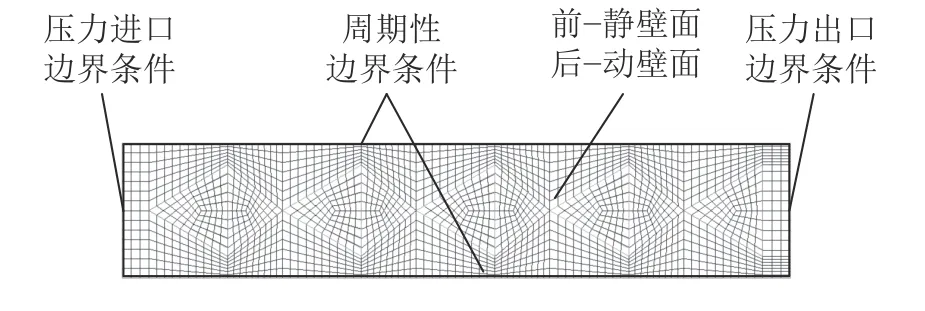
图2 计算域边界条件设置及网格示意Fig. 2 Boundary conditions and mesh of calculate domain

表2 计算参数
Tab. 2 Calculating Parameters

参数数值u/(m·s-1)±3、±6、±10、±15、±20 pin/MPa0.2～2.3 pout/MPa0.1润滑油黏度μ /(Pa·s)0.012润滑油密度ρ/(kg·m-3)850

1.2 FLUENT求解器设置

首先，判断理想情况下的流动状态。平行平板间流体的雷诺数

Re

计算方式如下：

另外，本文基于以下计算假设：1）忽略体积力的作用；2）流体在界面上无滑动；3）润滑油为牛顿流体；4）与黏性力相比，忽略惯性力；5）润滑剂黏度保持不变。

采用Fluent软件进行计算，主要求解参数设置如表3所示。

表3 Fluent主要求解参数设置
Tab. 3 Solution parameters in Fluent

参数模型数值方法Multiphase modelMixture Cavitation modelZwart-Gerber-Belamri Pressure-Velocity coupling schemeSIMPLEC Pressure discretizationPRESTO Momentum discretizationQUICK Volume FractionQUICK

工况包括速度和压力，本文主要研究了不同方向的速度、不同压差（Δ

p

=

p

–

p

）下三角形微孔在往复运动时的性能。

摩擦系数μ 的计算公式如下：

式中，

F

为摩擦力，

F

为承载力，表达式如下：

式（3）～（4）中，τ为剪切力，

p

为压力，

A

为摩擦副接触面积。

1.3 计算模型验证

计算模型在油膜厚度方向（

z

方向）的尺寸级别为微米级，在

x

方向和

y

方向尺寸级别为毫米级，涉及到跨尺度网格划分问题。为了保证计算结果的准确性，进行了网格跨尺度无关性分析。表4为不同的最大网格尺寸下，承载力

F

与出口流量

Q

的数值大小。

表4 最大网格尺寸对和的影响
Tab. 4 Effect of max element on and

最大尺寸/mmF/NQ/(10–6 kg·s–1)0.0010.2335.29 0.0020.2335.29 0.0040.2325.29 0.0060.2335.29 0.0080.2355.28 0.0100.2385.27 0.0150.2425.43 0.0200.2445.41

首先确定网格尺寸，如表4所示，最大网格尺寸的精度为0.001 mm时，最大网格尺寸小于等于0.002 mm时承载力

F

与出口流量

Q

不再变化，因此最大网格尺寸定为0.002 mm。10种分层方案的承载力

F

与出口流量

Q

如图3所示。

F

最大误差为0.72%，

Q

最大误差为1.06%，整体差异非常小。 方案“2-4”表示在

z

方向上油膜

h

分为两层网格，微孔深度

h

分为4层网格。考虑到计算效率及网格划分方便程度，最终选择了方案“2-4”。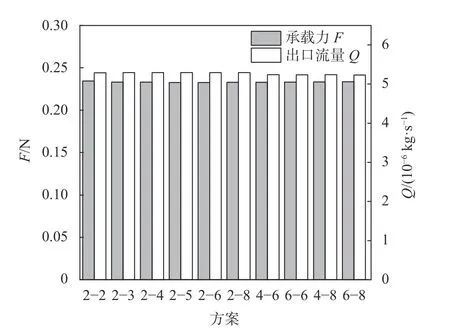

图3 网格层数对F和Q的影响Fig. 3 Effect of grid layers on F and Q

文献[23]对微孔的空化区域进行了实验与数值计算的对比研究，数值计算的结果与实验现象保持一致。为了验证计算模型的正确性，建立与文献[23]相同的微孔模型并以相同参数计算，对比结果如图4所示。由图4可见：本文计算出的压力分布与文献[23]基本一致，中心线压力平均相对误差为4.57%。

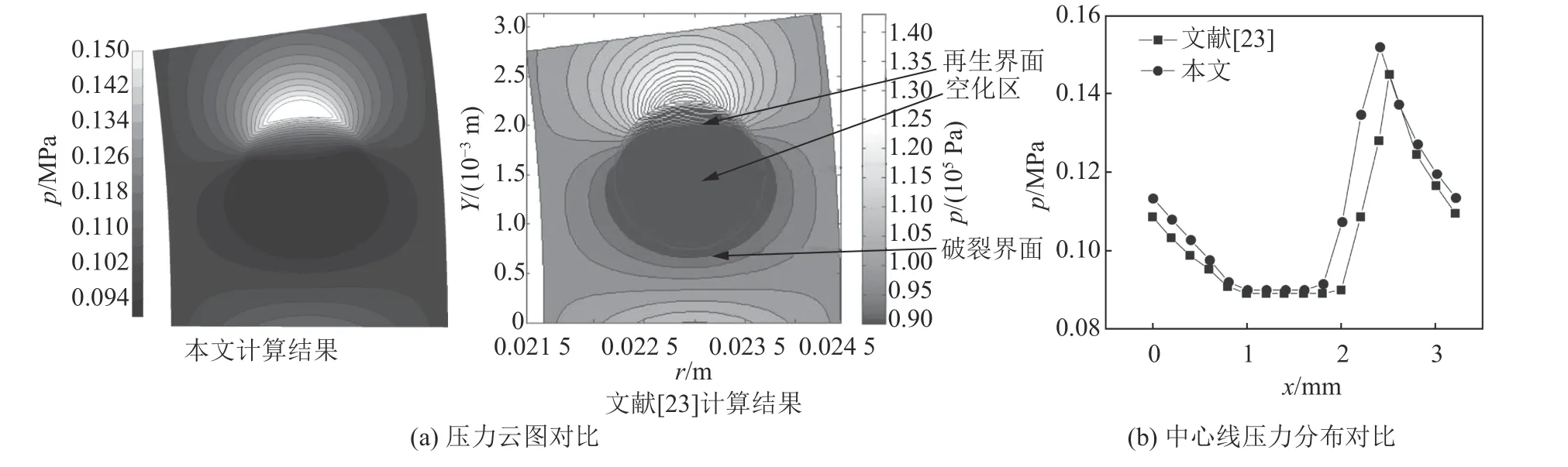
图4 计算模型与文献[23]压力分布对比Fig. 4 Comparison of pressure distribution between present model and Reference [23]

2 三角形微孔的两向异性

图5（a）为三角形微孔摩擦副在正反向运动时的摩擦系数随压差的变化曲线。定义正向运动的摩擦系数为μ，反向运动的摩擦系数为μ，正向运动与反向运动的摩擦系数差异δ=(μ–μ)×100%/μ。图5（b）为δ随Δ

p

的变化。从图5中可看出，整体情况μ≤ μ。当Δ

p

∈{0.2 MPa, 0.3 MPa,···,0.8 MPa}时，δ ≥ 0；其中，当Δ

p

为0.3 MPa时，δ达到最大，为31.68%。当Δ

p

＞0.8 MPa时，δ趋近于0。

图5 三角形微孔的两向异性（|u|=10 m/s，hp=4 μm）Fig. 5 Anisotropy of triangular dimple (|u|=10 m/s，hp=4 μm)

δ的出现是三角形的不对称性造成的。图6为三角形微孔不同形式的楔。当润滑油流经等边三角形微孔，如图6所示，∠

A

、∠

B

、∠

C

形成了3个楔。润滑油从大口流向小口，形成收敛间隙，流体沿收敛间隙流动将产生正压力。由于这3个楔与线速度

u

之间的夹角不一样，所以产生的楔效应也不一样。正向运动时（+

u

），润滑油从

BC

边流向∠

A

，楔

A

具有明显收敛性，将引起压力的上升，进一步增大承载力；在楔

B

和楔

C

位置，润滑油从小端流向大端，楔

B

和楔

C

为发散形楔，将引起压力下降，但发散性不强。反向运动时（–

u

），楔

A

具有明显发散性，楔

B

和楔

C

则为收敛楔，且收敛性不及正向运动时的楔

A

。当三角形微孔的方向角为0°时（对应本文正向运动），承载力最大；当方向角为60°（对应反向运动）时，承载力最小。由式（2）可知，承载力与摩擦系数负相关，正向和反向运动时的不同楔效应导致了摩擦系数大小的差异，即在一定范围内，δ ＞0。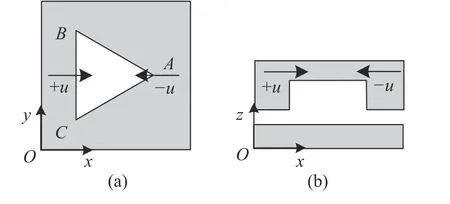

图6 三角形微孔的楔Fig. 6 Wedge of triangular dimple

随着Δ

p

不断增大，δ的趋势为先增大后减小，这是由于静压的改变对动压造成了影响。如图1所示，在三角形孔的几何收敛点处作直线

l

，直线

l

上的压力分布可以反映出静压对动压的影响程度。图7为直线

l

上的压力分布。

图7 直线l上压力分布（u=+10 m/s，hp=4 μm）Fig. 7 Pressure distribution on line l (u=+10 m/s，hp=4 μm)

图7中虚线表示摩擦副没有相对运动时，线

l

上的压力分布，即理想静压；Δ

p

相同时虚线与实线之间的区域即为动压效应提升的压力。当Δ

p

从0.1 MPa到0.3 MPa，由于压差增大使入口流量增加，加强了动压效应，使δ增大。当Δ

p

从0.3 MPa到1.0 MPa，压力整体被拉伸升，动压效应带来的压力提升效果被静压稀释，导致δ减小。随着静压继续增大，动压效应对压力分布的影响将逐渐被静压削弱并取代，最终压力分布由静压主导，δ趋近于0。

3 运动速度对两向异性的影响

图8为不同速度下，两向运动摩擦系数差异δ随压差Δ

p

的变化曲线。从图8中可看出，不同速度下的曲线趋势类似，Δ

p

较小时，δ较大；Δ

p

较大时，δ趋近于0。|

u

|为6、10、15、20 m/s时，δ都存在一个峰值，分别为31.92%、31.68%、30.14%、29.16%。|

u

|为3 m/s时，δ没有形成峰值。当|

u

|增大时，峰值对应的Δ

p

也增大，且δ＞0时，对应的Δ

p

区间也变宽，|

u

|为3、6、10、15、20 m/s时对应的Δ

p

的区间分别为[0.1,0.2]、[0.1,0.4]、[0.1,0.8]、[0.2,1.2]和[0.3,1.5]，说明速度绝对值增大拓宽了三角形微孔两向异性的应用范围。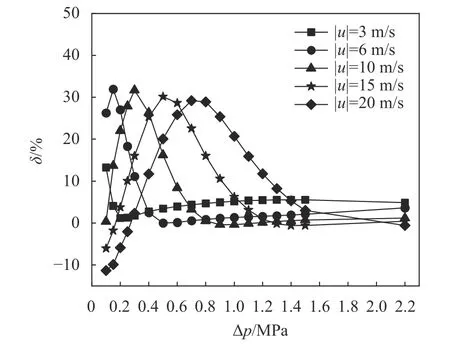

图8 不同速度下δ随Δp的变化（hp=4 μm）Fig. 8 δ versus Δp at different velocities (hp=4 μm)

|

u

|为3 m/s时，三角形微孔表现出两向异性的Δ

p

区间很小，在Δ

p

≥0.2 MPa时，δ便趋近于0。这是由于运动的速度较低时，空化面积较小，微孔的动压承载能力对承载力的影响有限，占主导的因素是静压。图9为不同速度下承载力

F

随压差的变化情况，|

u

|为3 m/s时，

F

几乎呈一条直线，说明Δ

p

是影响承载力的主要因素。而当

u

为+10 m/s和+20 m/s时，曲线有一定的曲度，且有曲度的Δ

p

区间[0.2,0.5]、[0.3,1.5]与图8中δ较大的Δ

p

区间吻合。由于δ是两向运动时的不同动压造成的，增加速度大小能够增强微孔的动压作用，因此能增强三角形微孔的两向异性。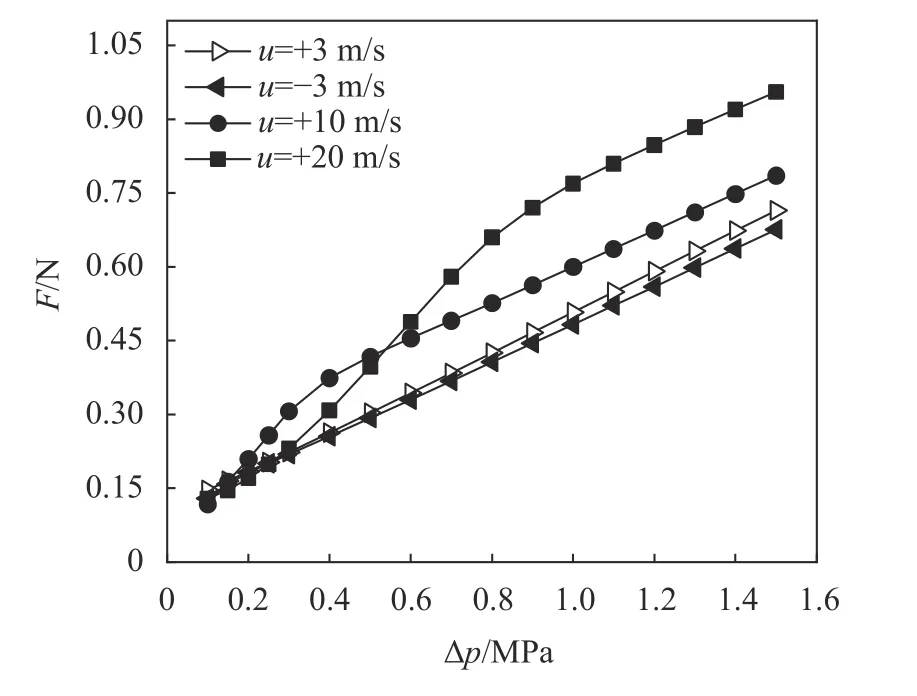

图9 不同速度下F随Δp的变化（hp=4 μm）Fig. 9 F versus Δp at different velocities (hp=4 μm)

4 孔深对两向异性的影响

图10为不同孔深时，δ随压差Δ

p

的变化曲线。从图10中可以看出，所有曲线趋势类似，峰值出现在曲线的前半部分，曲线后半部分趋近于0。当

h

为3、4、5、6 μm时，曲线的峰值分别为35.5%、31.7%、25.6%、30.1%，且

h

为6 μm时，峰值对应的Δ

p

为0.15 MPa，其余3条曲线峰值对应的Δ

p

都为0.3 MPa。

图10 不同孔深下δ随Δp的变化（|u|=10 m/s）Fig. 10 δ versus Δp at different dimple depths (|u|=10 m/s)

孔深对两向异性的影响取决于孔深对动压效应的影响。承载力或摩擦系数都能反映出这一影响。同一工况下，会有最适合的孔深使承载力最大，说明该孔深产生的流体动压效果较其他孔深更好。而δ正是由于三角形微孔两向运动下不同楔效应造成的不同动压效果引起的，当Δ

p

＜0.2 MPa时，孔深

h

为6 μm比其余3种孔深更好，

h

为6 μm时的δ大于其余3种孔深时的δ；Δ

p

＞0.2 MPa时，

h

为3 μm更好，

h

设为3 μm时的δ大于其余3种孔深时的δ。如图11所示，承载力

F

随Δ

p

的变化曲线证实了这点。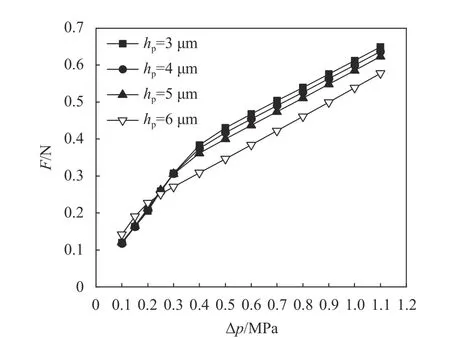

图11 不同孔深下F随Δp的变化（u=+10 m/s）Fig. 11 F versus Δp at different dimple depths (u=+10 m/s)

5 三角形微孔与圆形微孔的对比

图12为三角形微孔与圆形微孔在同一工况下的压力云图对比，可见正向运动三角形微孔的高压区域范围更大。

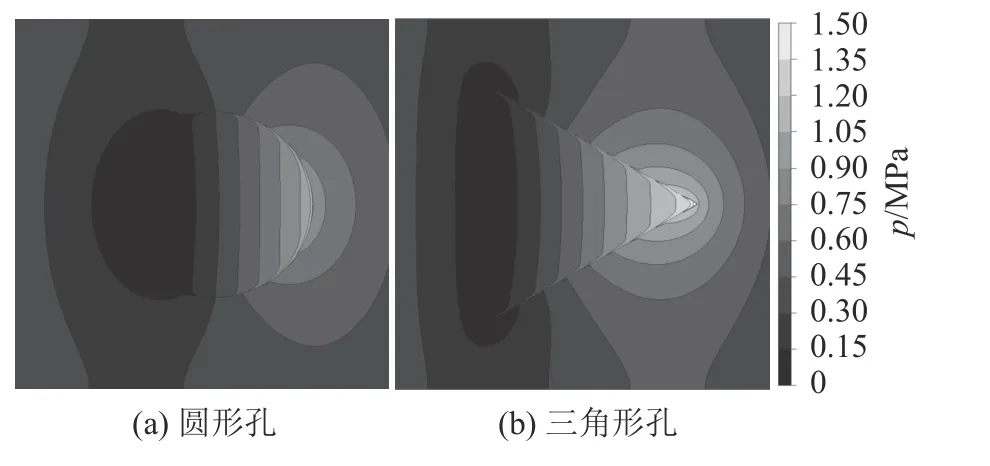
图12 压力分布云图（u=+10 m/s，hp=4 μm，Δp=0.3 MPa）Fig. 12 Pressure distribution contours (u=+10 m/s，hp=4 μm，Δp=0.3 MPa)

图13为当

h

为4 μm、

S

相同时，圆形微孔摩擦副与三角形微孔摩擦副的摩擦系数对比曲线。不同的

u

、

h

下对比曲线都类似于图13，只是δ显著大于0的区间随具体情况改变。当Δ

p

为0.3 MPa时，圆形微孔摩擦副的摩擦系数比三角形微孔摩擦副正向运动时的摩擦系数最大高出17.96%。而在高压区，相比于动压，静压变为影响摩擦系数的主要因素，且圆形微孔的面积密度、深度都与三角形微孔相同，所以表现为图13中所示的重合趋势。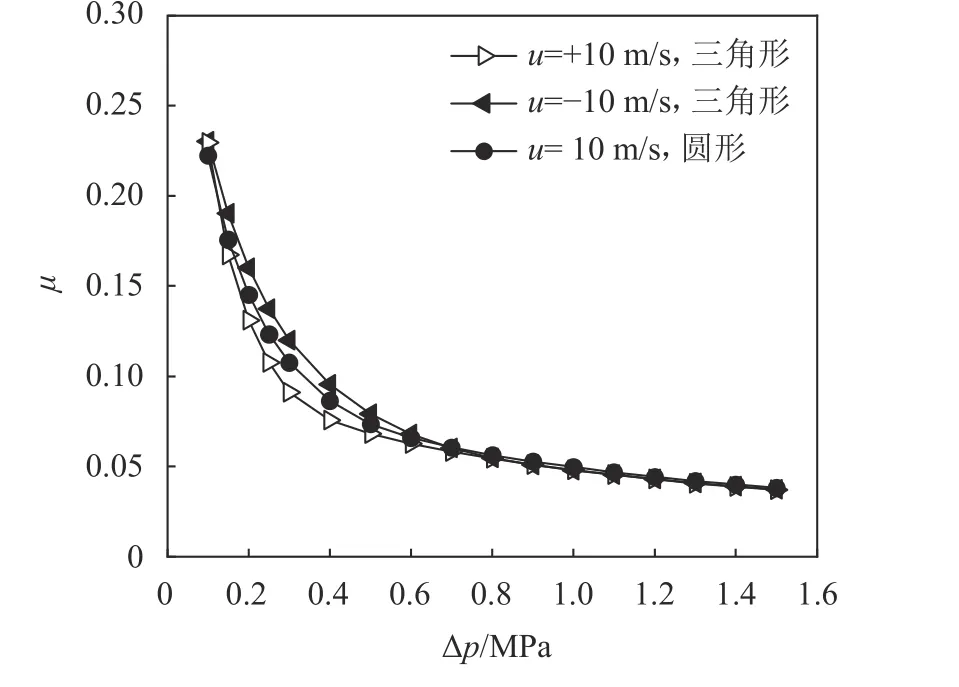

图13 三角形微孔与圆形微孔摩擦系数的对比（hp=4 μm）Fig. 13 Comparison of friction coefficients between triangular and circular dimples (hp=4 μm)

三角形微孔正向运动在较低压差区的性能优于圆形微孔，其反向运动在其余压差下都与圆形微孔相当。这样的两向异性特点正好契合了一些往复运动的机构在做功侧运动时压力高，返回时压力低的工况特性。因此，三角形微孔能够提供比圆形微孔更好的摩擦性能，即利用微孔的两向异性满足了工况的两向异性。

表5为

h

为4 μm时、不同的两向压差下，三角形孔摩擦副和圆形孔摩擦副的摩擦系数对比。表5中，Δ(Δ

p

)表示正向运动和反向运动的压差差异，Δ(Δ

p

)=Δ

p

–Δ

p

，Δ

p

为正向运动的压差，Δ

p

为反向运动的压差；分别表示三角形微孔和圆形微孔正向运动和反向运动的摩擦系数平均值，δ(μ)为三角形微孔和圆形微孔的摩擦系数对比，δ(μ)= ()×100%/。当Δ(Δ

p

)为0，即两向运动的压差相同时，综合来看，三角形微孔的性能略优于圆形微孔；当Δ(Δ

p

)≠0时，三角形的两向异性优势便开始显现：Δ(Δ

p

)为0.4 MPa时，δ(μ)最大为11.1%（随着Δ(Δ

p

)增大，δ(μ)的最大值也增大），Δ(Δ

p

)为1.0 MPa时，δ(μ)最大为13.3%，且Δ(Δ

p

)≠0时，除Δ

p

为0.1 MPa时，三角形微孔的性能略低于圆形孔外，每组其余两向压差下均优于圆形微孔。可以看出，在

h

为4 μm，|

u

|为10 m/s的情况下，三角形微孔更适合Δ(Δ

p

)较大的两向工况。

表5 不同工况下的三角形和圆形孔摩擦系数对比（=4 μm，||=10 m/s）
Tab. 5 Friction coefficients comparison of triangular and circular dimples under different working conditions (=4 μm，||=10 m/s)

Δpp/MPaΔ(Δp)=0 MPaΔ(Δp)=0.4 MPaΔ(Δp)=0.8 MPaΔ(Δp)=1.0 MPa¯μt¯μcδ(μ)/%¯μt¯μcδ(μ)/%¯μt¯μcδ(μ)/%¯μt¯μcδ(μ)/%0.10.2300.222–3.30.1540.148–4.20.1400.138–1.90.1370.135–2.0 0.20.1460.145–0.20.1000.1066.00.0890.0978.90.0870.0958.9 0.30.1060.1071.80.0760.08411.10.0680.07713.20.0660.07513.3 0.40.0850.0861.10.0650.0719.60.0590.06510.30.0570.06310.3 0.50.0740.073–0.20.0590.0636.20.0540.0586.00.0530.0565.9 0.60.0650.0660.60.0550.0584.40.0510.0533.9——0.70.0590.0612.20.0520.0543.70.0480.0493.2——0.80.0550.0563.30.0490.0503.4——0.90.0510.0533.70.0460.0473.2——1.00.0480.0503.70.0430.0453.0——1.10.0450.0473.40.0410.0422.8——1.20.0430.0443.2——1.30.0410.0423.0——1.40.0390.0402.7——1.50.0370.0382.5——

采用同样的方法，可以总结

h

为6 μm时，不同的两向压差下三角形孔摩擦副和圆形孔摩擦副的摩擦系数对比（限于篇幅，没有给出数据表），当

h

为6 μm时，相比于

h

为4 μm，Δ(Δ

p

)相同时，δ(μ)最大值变小，且最大值出现在Δ

p

为0.1 MPa时，即适宜的工况有改变。可以推理，当三角形微孔的孔深、密度、方向角度不同时，适宜的工况会不同，使得三角形微孔的适用范围更加广泛。

6 结 论

1）三角形微孔带来的两向异性在一定的范围内存在，当孔深

h

为4 μm，|

u

|为3、6、10、15、20 m/s时，对应δ＞0的Δ

p

区间分别为[0.1,0.2]、[0.1,0.4]、[0.1,0.8]、[0.2,1.2]和[0.3,1.5]，速度增大会使此范围变大。2）当

h

不同时，出现两向异性的范围也不相同。当|

u

|为10 m/s，

h

为3、4、5、6 μm时，对应δ＞0的Δ

p

区间分别为[0.1,0.9]、[0.1,0.8]、[0.1,0.7]、[0.1,0.4]，δ分别为35.5%、31.7%、25.6%、30.1%。3）当摩擦副两向运动时，应设计三角形尖端朝向压差较低侧，利用三角形微孔的两向异性能够使其提供比圆形微孔更好的摩擦性能，

h

为4 μm时其两向运动的平均摩擦系数最多比圆形微孔减少13.3%。