隧道高强钢管格栅与钢筋格栅承载特性室内模型试验

宋 远，黄明利*，张旭东，张志恩

(1.北京交通大学 城市地下工程教育部重点实验室，北京 100044；2.中铁十一局集团有限公司，湖北 武汉 430061)

进入21世纪，中国交通基础设施、水利水电等领域地下工程建设需求增加，隧道工程等基础建设迎来了前所未有的发展机遇。中国西部山区隧道工程地质条件和围岩力学性质极端复杂，所处地域构造运动活跃，施工过程中出现的高地应力软岩大变形问题成为隧道施工的常见灾害之一，严重制约隧道工程的施工建设安全与长期运营稳定，给隧道施工期间的灾害防控带来诸多新的挑战。

针对高地应力软岩隧道大变形控制技术难题，国内外众多学者开展了大量的理论探讨和试验研究，取得了丰硕的研究成果，并积累了宝贵的经验。Oreste等针对陶恩隧道在穿越高地应力环境下软岩地层时，发生持续挤压变形，频繁出现钢拱架扭曲、断裂，喷混凝土开裂、掉块，支护失稳及侵限破坏等现象，通过采取长锚杆加固、可缩式钢架、喷层预留变形量等措施成功抑制围岩变形；张祉道针对在穿越高地应力条件下的煤系软弱地层时，南昆铁路家竹菁隧道产生挤压性大变形，严重威胁隧道施工安全，通过采用优化隧道断面形状、施作长锚杆、设置可缩式钢架，双层模注混凝土衬砌等技术措施，达到了良好的控制效果；李国良、雷军等针对在高地应力软弱围岩地质开挖过程中，兰新铁路乌鞘岭长大深埋隧道挤压大变形显著，初期支护开裂挤压破坏严重，通过设置迂回导坑释放围岩压力，多重支护加强支护刚度，优化台阶长度，中长锚杆加固围岩，合理预留变形量，超前锚管预支护等方法有效控制了围岩大变形；刘高、杨木高等针对兰渝铁路木寨岭隧道穿越极高地应力软弱围岩区，初期支护发生多次大变形，拆换频繁，二次衬砌施作后出现不同程度开裂的情况，通过采用超前导洞扩挖应力释放，圆形四层支撑体系、长锚杆锚索和径向注浆加固，超前预支护及预加固等变形控制方案，改善了支护结构受力，限制了变形增长；成兰高铁某隧道工程穿越汶川高烈度区，李术才等借鉴高层建筑核心筒理念，设计实施了钢格栅混凝土核心筒支护结构形式，有效控制了隧道变形。

根据国内严重大变形隧道治理经验，可从支护理念及配套施工技术上重新审视大变形隧道的控制思路，提出适用于大变形隧道的支护体系。对围岩大变形的处置，从支护设计理念和支护系统组成而言，可分为柔性让压支护和及时强支护两类，柔性让压支护理念则利用一定的柔性支护措施允许围岩产生一定的形变以释放部分围岩压力，减轻支护结构承受荷载，例如让压锚杆、可缩性钢架、多重支护及超前导洞应力释放等。及时强支护理念通过及时架设大刚度、高强度的支护结构控制围岩变形，例如空间钢网架支护、高强钢筋格栅拱架支护、钢管混凝土支护、装配式弧板支护、高强预应力锚索一次支护、长大预应力锚杆–锚索协同支护等措施。上述研究成果极大推动了中国软岩大变形隧道工程支护技术的发展与革新，助力隧道等交通基础设施建设。目前，国内外学者对钢筋格栅的结构形式、力学性能及钢筋格栅与喷射混凝土的复合支护特性进行了研究。Baumann等设计出了一种8字结腹筋构造的三肢格栅拱架，通过开展一系列的格栅拱架现场应用试验，验证了该结构设计的合理性；Nomikos等对未喷混凝土情况下的三肢格栅拱架的受力特性进行了分析，阐述了不同参数下格栅拱架的力学响应问题；Kim等设计出一种格构形式的四肢格栅拱架，结合四点弯曲试验和数值模拟，与三肢格栅拱架进行对比，评估了二者在极限承载力及结构稳定性方面的差异；Lee等开展对高强度格栅拱架的力学性能研究，得出了合理的结构设计参数，并验证其具备良好的稳定性和经济性；Qiu等为评价四肢格栅拱架极限承载力与其部件成本之间的关系，引入优化指标参数，就腹筋直径和焊缝长度等因素对格栅拱架的力学性能影响规律进行了系统化研究；于富才等对高强钢筋格栅混凝土复合支护的力学特性、适用性进行了研究，得出高强钢筋的应用显著提高了格栅混凝土复合支护结构的极限承载力和极限变形能力，能够适用于特殊围岩或地质条件很差的隧道工程。然而，针对高强钢管代替主肢钢筋的研究，至今隧道工程界仍鲜有涉及，对钢管格栅在初期支护体系中的作用机理缺乏必要的讨论。

初期支护作为承担施工阶段全部荷载的主要承载结构，软岩大变形隧道的稳定性控制对支护结构性能提出了更高的要求，为尽快提供有效支护抗力，控制围岩变形，减小松动荷载，可设计采用高强度、大刚度的新型拱架结构，达到强化初期支护的目的。为此，本文设计了1种以高强无缝钢管为主材的4肢钢管格栅初期支护结构，通过室内模型试验方法对该新型支护结构的承载特性和变形破坏机制进行深入分析，以期为软岩大变形隧道安全施工建设提供新思路、新方法。

1 试验背景

随着西南地区交通建设步入新的发展阶段，穿越高地应力软弱围岩地段的深埋隧道不断出现，尽管采用超前加固、分部开挖等措施保障施工安全，仍然有发生拱架扭曲破坏、喷射混凝土开裂，甚至隧道坍塌等工程灾害（图1）。成兰铁路跃龙门隧道穿越龙门山山脉，不良地质多变，软岩大变形显著。跃龙门隧道采用双洞分修，左、右线全长近20 km，最大埋深为1 445 m。发生挤压性围岩大变形区段有岩浆热液侵入、多次褶曲等构造活动，地应力高达20.0～31.5 MPa。在施工后期通过遵从“主动控制”的理念，采取“双层支护”等措施，及时有效支护，较好地抑制了围岩变形和破碎范围的发展。

图1 混凝土掉块和钢架扭曲破坏Fig. 1 Shotcrete block falling and steel arch distortion

本文结合实际工程需要，立足软岩大变形隧道施工控制技术难题，利用高强度无缝钢管代替主肢钢筋作为格栅拱架的主受力件，发挥主肢钢管高强度、高韧性的特点，同时保留格栅拱架与喷射混凝土较好的黏结性能，与钢筋格栅开展对比模型试验研究，为该新型支护结构的参数设计及后续工程应用提供借鉴。

2 钢格栅试件抗弯力学特性试验

2.1 钢格栅试件设计

钢格栅试件构造型式如图2所示。新奥法施工隧道广泛采用腹筋为8字结或π形设计形式的4肢格栅拱架，抗压主筋和抗拉主筋多为同直径、同材质带肋钢筋，直径一般在22～32 mm，腹筋直径多为10～14 mm，具体构造如图2（a）、（b）所示。此次试验设计加工腹筋为π形设计形式的格栅拱架，构件总长为3.2 m，主筋直径为32 mm，π形和U形连接筋直径为14 mm，三者材质均为HRB400，箍筋直径为8 mm，材质为HPB300。

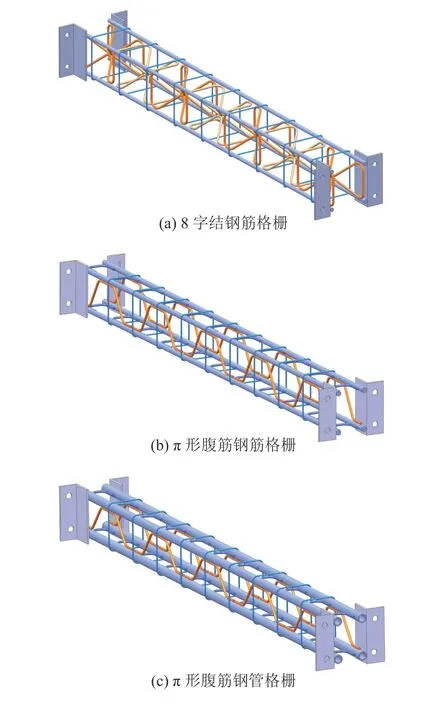
图2 试件构造型式Fig. 2 Structural types of the specimens

新型钢管格栅，主要部件包括高强度无缝薄壁圆钢管，π形筋+U形筋组成的架立件，通过焊接工艺将主受力件与架立件形成整体。钢管选用Q420无缝钢管，钢管外直径为50 mm，壁厚6 mm；架立件采用HRB400带肋钢筋，直径为14 mm；箍筋采用HPB300光圆钢筋，直径为8 mm。钢管格栅具体构造如图2（c）所示。

试件的设计参数见表1，钢材材料性能见表2。为了更好地研究两种试件的经济效益差异，对二者每延米造价进行了对比分析，得到的统计数据见表3，其中，成本核算已将加工成本和人工成本纳入。分析可知，相较于钢筋格栅，钢管格栅每延米质量基本相同，但每延米造价提高14.14%。

表1 主要构造参数
Tab. 1 Main structural parameters

构件类型钢管直径×壁厚/(mm×mm)主筋直径/mm构件长度/mm腹筋直径/mm箍筋直径/mm截面尺寸/(mm×mm)平均每延米质量/(kg·m–1)惯性矩Ix/cm4惯性矩Iy/cm4钢筋格栅—323 200148200×26431.894 349.372 290.50钢管格栅50×6—3 200148200×26432.193 880.011 947.88

表2 钢材力学性能
Tab. 2 Mechanical properties of steels

材料弹性模量E/GPa屈服强度fy/MPa强度设计值f/MPa抗拉强度fu/MPa伸长率(ΔL·L–1)/%Φ8 mm钢筋206311.90267.54436.2329.39 Φ14 mm钢筋198430.34353.76576.8123.60 Φ32 mm钢筋201445.64367.35592.5019.28 Φ50 mm×6 mm钢管205457.78398.64604.6125.47

表3 成本核算
Tab. 3 Cost accounting

主肢钢管(钢筋)π形筋U形筋箍筋构件类型总造价/元 每延米造价/(元·m–1)用量/kg 单价/(元·t–1)用量/kg 单价/(元·t–1)用量/kg 单价/(元·t–1)用量/kg 单价/(元·t–1)钢筋格栅 80.814 1009.433 9008.243 9003.593 300412.08128.78钢管格栅 83.334 7508.863 9007.283 9003.523 300470.38146.99

2.2 钢格栅试件加载方案

通过4点纯弯曲试验对比分析钢筋格栅与新型钢管格栅的钢筋/钢管应力、跨中挠度、极限承载力及破坏形态等力学特性。在此基础上，进一步研究二者与喷射混凝土耦合作用下的受力及变形破坏规律。

图3为两种构件的4点纯弯曲加载示意图。支座位置距构件两端各100 mm，在载荷分配梁下左右对称布置加载垫块实现竖向荷载的传递，垫块距跨中450 mm，利用竖向液压千斤顶施加垂直荷载，构件的截面尺寸均为200 mm×264 mm（图4）。

图3 4点纯弯曲加载示意图Fig. 3 Schematic diagram of 4-point pure bending loading

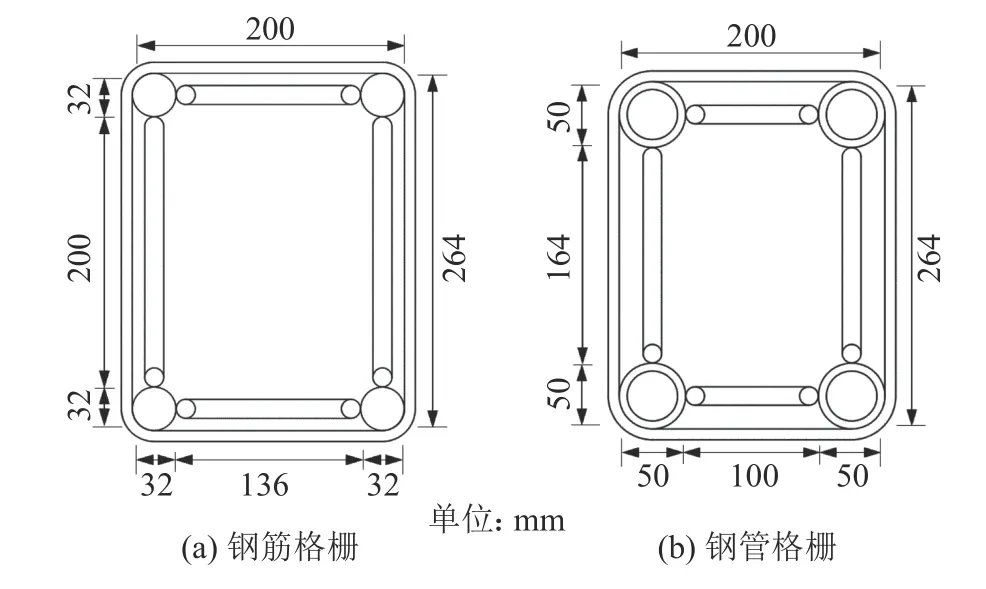
图4 钢筋格栅和钢管格栅截面尺寸Fig. 4 Section size of lattice girder and steel tube grid

室内试验在Y32–500A四柱式液压加载系统上进行，竖向最大公称压力可达5 000 kN，滑块行程为900 mm。试验前，对构件进行几何和物理对中。加载分3步进行：首先，对构件进行预加载，保证构件和加载装置接触良好；随后，采用分级加载方式，每级荷载增量为10 kN，每级加载后并保压持续3 min；当荷载压力不再继续增长后，改为位移加载方式，加载速率为1 mm/min，直至构件失稳破坏。钢格栅试件试验过程中具体加载情况如图5所示。

图5 钢格栅试件加载试验Fig. 5 Loading tests of steel grid specimens

2.3 测点布置

在钢筋格栅和钢管格栅构件的1/2截面和1/4截面位置，沿横向和纵向粘贴金属应变片共16个，中部π形连接筋表面粘贴应变片8个，设置3个挠度位移计。具体测点布设情况如图6所示。

图6 钢格栅试件测点布置图Fig. 6 Layout of measuring points of steel grid specimens

2.4 钢格栅试件试验过程及现象

图7为钢筋格栅试件的室内加载变形破坏形态。由图7可见：在加载过程中试件展现出左右对称变形，在加载初期，试件未发生明显变化，当弯矩增加至37.28 kN·m时，主肢钢筋在加载处出现较明显的弯曲变形，同时下部的π形筋受荷载挤压变形幅度大；当弯矩增加至55.13 kN·m时，主肢钢筋变形进一步加剧，表现出折线形压弯破坏，π形筋变形显著，并在焊接点附近出现钢筋破断；加载完成后卸载，试件的回弹变形量较小。

图7 钢筋格栅破坏形态Fig. 7 Failure mode of lattice girder

图8为钢管格栅试件的室内加载变形破坏形态。由图8可见：试件表现为左右对称变形，加载初期，试件无明显变化，当弯矩增加至65.63 kN·m时，主肢钢管产生一定程度的弯曲变形，但幅度很小，此时下部的π形筋变形亦不明显；当弯矩增加至98.18 kN·m时，主肢钢管弯曲幅度进一步加大，表现为平滑曲线形破坏，π形筋变形明显，未出现钢筋破断；加载完成后卸载，测得的回弹变形量较大。

图8 钢管格栅破坏形态Fig. 8 Failure mode of steel tube grid

综上分析可知，钢筋格栅和钢管格栅在破坏形态、极限承载力及回弹量方面存在较明显的差异，其中钢管格栅表现出更好的变形特性及韧性特征。

2.5 钢格栅试件试验结果分析

2.5.1 弯矩–应变曲线

图9为钢筋格栅主肢钢筋的弯矩–应变关系曲线，图10为钢管格栅主肢钢管的弯矩–应变关系曲线，均包括1/2和1/4这2个监测断面。

图9 钢筋格栅试件弯矩–应变关系曲线Fig. 9 Bending moment-strain relationship curves of lattice girder

1）钢筋格栅主筋

由图9（a）可见：钢筋格栅上主筋测点SBS–1和SBS–3起初表现为压应变，当弯矩增加到一定程度，转变为拉应变，构件失稳破坏时拉应变为502×10和834×10，应力值约为103.4和171.8 MPa；而钢筋格栅上主筋测点SBS–2和SBS–4起初表现为拉应变，随后转变为压应变，最大压应变分别为–150×10和–134×10，应力值约为30.9和27.6 MPa；钢筋格栅下主筋测点SBS–5和SBS–7始终承受拉应力，构件失稳破坏时拉应变分别为1 546×10和2 471×10，应力值约为318.5和509.0 MPa，测点SBS–7超过了钢材的屈服强度；钢筋格栅下主筋测点SBS–6和SBS–8始终承受压应力，最大压应变分别为–364×10和–548×10，应力值约为75.0和112.9 MPa。

由图9（b）可见：钢筋格栅上主筋测点SBS–1和SBS–3主要表现为拉应变，加载后期应变增速明显，构件失稳破坏时拉应变分别为3 078×10和2 857×10，应力值约为634.1和588.5 MPa，超过了钢材的屈服强度；钢筋格栅上主筋测点SBS–2和SBS–4承受拉应力，最大拉应变分别为–730×10和–613×10，应力值约为150.4和126.3 MPa；钢筋格栅下主筋测点SBS–5和SBS–7承受拉应力，构件失稳破坏时拉应变分别为2 307×10和2 206×10，应力值约为475.2和454.4 MPa，超过了钢材的屈服强度；钢筋格栅下主筋测点SBS–6和SBS–8承受压应力，最大压应变分别为–471×10和–423×10，应力值约为97.0和87.1 MPa。

2）钢管格栅钢管

由图10（a）可见：钢管格栅上主肢钢管测点STS–1和STS–3起初表现为压应变，随着弯矩不断增加，应力状态逐渐向拉应力转变，构件失稳破坏时拉应变为287×10和602×10，应力值约为59.1和124.0 MPa；测点STS–2和STS–4表现为拉应变，构件失稳破坏时应变为183×10和152×10，应力值约为37.7和31.3 MPa；钢管格栅下主肢钢管测点STS–5和STS–7始终承受拉应力，达到极限承载状态时应变为2 325×10和2 588×10，应力值分别为479.0和533.1 MPa，超过了钢材的屈服强度；测点STS–6和STS–8始终承受压应力，最大压应变分别为–659×10和–1 373×10，应力值分别为135.8和282.9 MPa。

由图10（b）可见：钢管格栅上主肢钢管测点STS–1和STS–3起初表现为压应变，加载后期转变为拉应变，且应变增速明显，构件失稳破坏时拉应变分别为895×10和1 608×10，应力值约为184.4和331.2 MPa；测点STS–2和STS–4承受轻微的拉应力；钢管格栅下主肢钢管测点STS–5和STS–7承受明显的拉应力，构件失稳破坏时拉应变分别为1 489×10和1 025×10，应力值约为306.7和211.2 MPa；测点STS–6和STS–8承受压应力，构件失稳破坏时压应变分别为–479×10和–379×10，应力值约为98.7和78.1 MPa。

图10 钢管格栅试件弯矩–应变关系曲线Fig. 10 Bending moment-strain relationship curves of steel tube grid

3）π形筋

图11为钢筋格栅和钢管格栅π形筋弯矩–应变关系曲线。在初始加载阶段，应变值与弯矩大小之间呈线性增长关系，此时，应变增长速率较缓，当荷载增加到一定范围，应变增速有所加快，随后产生塑性变形，达到构件极限承载力时，应变值仍不断提高。

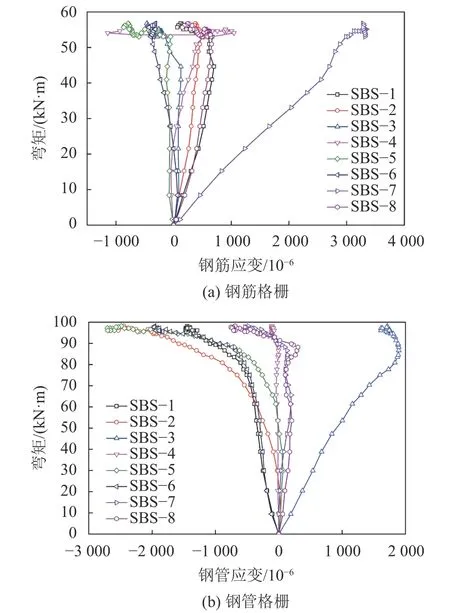
图11 钢筋格栅和钢管格栅π形筋弯矩–应变关系曲线Fig. 11 Bending moment-strain relationship curves of πshaped bar of lattice girder and steel tube grid

由图11（a）可见：对于钢筋格栅，测得的π形筋拉、压应变值基本处在–1 200×10～1 100×10的范围内，仅测点SBS–7应变值过大，超过材料的屈服强度，整体上π形筋的工作状态良好，能很好地起到力系的传递作用。

由图11（b）可见：对于钢管格栅，π形筋各测点主要表现为压应变，其中测点SBS–3承受较大的拉应力，构件失稳破坏时最大应变为1 896×10，应力为390.6 MPa；测点SBS–2承受较大的压应力，构件失稳破坏时最大应变为2 698×10，应力为555.8 MPa，超过材料的屈服强度，表明钢筋处于较高的应力状态，构件的屈服和破坏易率先在此发生。

综上分析可知：对于钢筋格栅和钢管格栅试件，截面不同，测点位置不同，应变大小和受力模式也随之发生变化。在加载初期，各个测点应变随弯矩呈线性增加；随着弯矩继续施加，达到弹性极限应变，材料产生初始屈服，应变增速明显加快，达到极限承载状态后，发生屈服的区域应变仍不断增大；钢筋格栅下主肢钢筋处于较高的应力应变状态，而钢管格栅主要是π形筋应力值较高，表明钢管格栅具有良好的受力性能和合理的结构型式。

2.5.2 弯矩–挠度曲线

图12为钢筋格栅和钢管格栅试件的弯矩–挠度曲线对比，试件中间位置的竖向位移作为跨中挠度，取值为正，跨中所受弯矩由荷载传感器采集到的压力换算得到。

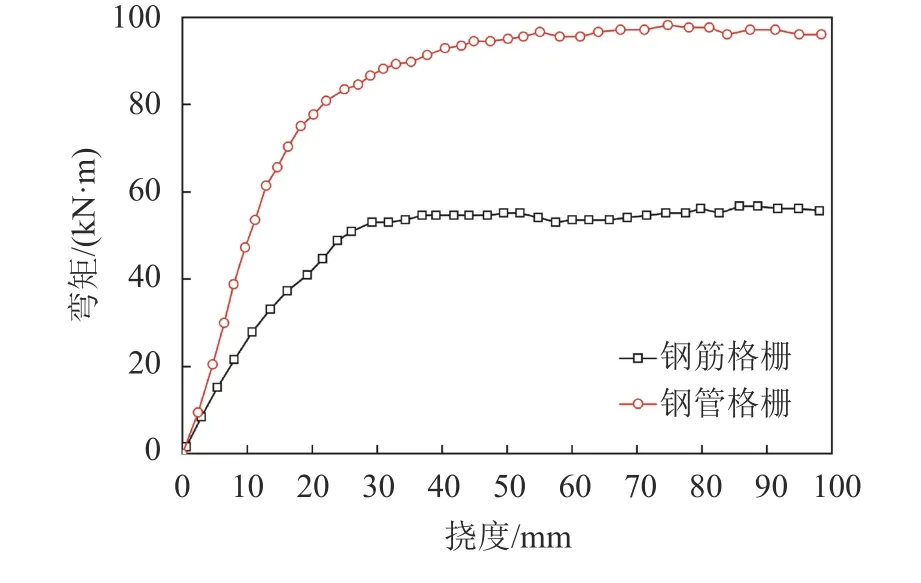
图12 钢筋格栅和钢管格栅弯矩–位移关系曲线对比Fig. 12 Bending moment-deflection relationship curves of lattice girder and steel tube grid

由图12可见：在整个弯矩–挠度历程曲线中，加载初期钢筋格栅和钢管格栅均处于弹性变形阶段，挠度随弯矩呈线性增加，钢筋格栅试件的挠度增长速率较快；弯矩继续施加，挠度增长速率逐渐提高，试件开始进入塑性变形阶段；达到极限承载力后，挠度位移迅速增长，但承载力保持稳定，并持续较长时间。钢筋格栅达到极限承载状态时的跨中挠度约为34.3 mm，对应的极限承载力为53.6 kN·m，而钢管格栅达到极限承载状态时的跨中挠度约为55.1 mm，对应的极限承载力为96.6 kN·m，为钢筋格栅的1.8倍，说明钢管格栅具备高强度高韧性的特点。

3 格栅混凝土试件抗弯力学特性试验

3.1 格栅混凝土试件设计

格栅混凝土试件总长亦为3.2 m，所使用钢材的材质、规格及尺寸等参数参照表1和2，喷射混凝土采用C25商品混凝土代替，上、下保护层厚度为43 mm，截面尺寸为300 mm×350 mm（见图13）。浇筑后的格栅混凝土试件如图14所示。

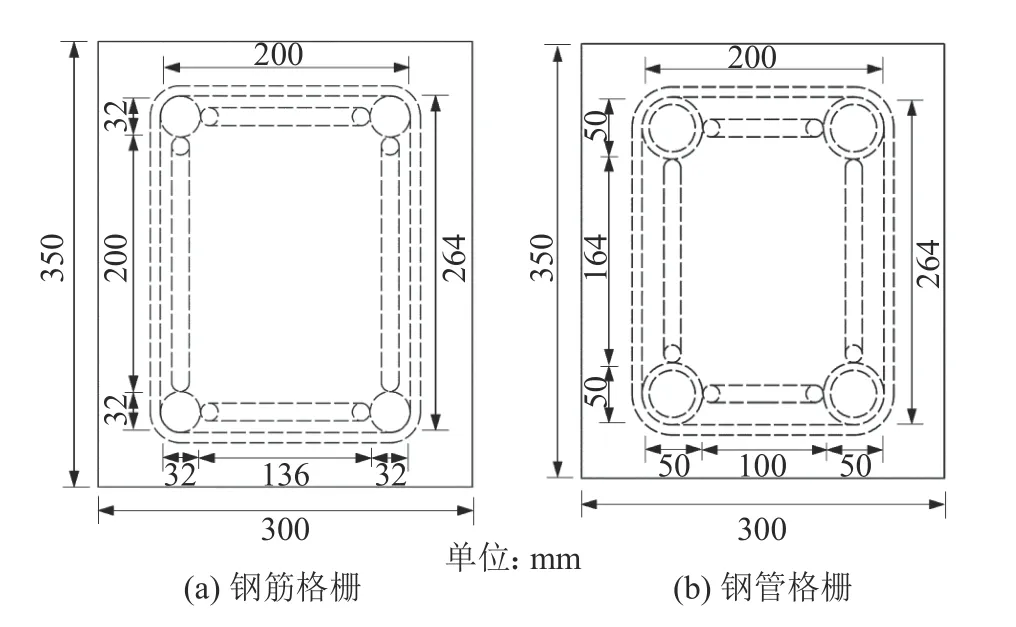
图13 格栅混凝土试件截面尺寸Fig. 13 Section size of grid concrete specimens

图14 浇筑后格栅混凝土试件Fig. 14 Grid concrete specimens after pouring

3.2 格栅混凝土试件加载方案

通过4点纯弯曲试验深入分析两种格栅混凝土试件在挠度、极限承载力及整个加载过程中的混凝土表面应力应变演化规律。室内试验同样在Y32-500A四柱式液压加载系统上进行，加载装置和加载控制方法与第2.2节相同。试验过程中具体加载情况如图15所示。

图15 格栅混凝土试件加载试验Fig. 15 Loading tests of grid concrete specimens

3.3 格栅混凝土试件测点布置

在钢筋格栅混凝土试件和钢管格栅混凝土试件的1/2截面和1/4截面位置，于上、下、前、后4个表面沿横向和纵向黏贴混凝土应变片共计32个，设置3个挠度位移计。格栅混凝土试件测点布设情况如图16所示。

图16 格栅混凝土试件测点布置Fig. 16 Layout of measuring points of grid concrete specimens

3.4 格栅混凝土试件试验过程及现象

通过室内试验得知，钢筋格栅混凝土试件和钢管格栅混凝土试件在破坏形态和裂缝扩展规律方面存在较大区别。

图17为钢筋格栅混凝土试件和钢管格栅混凝土试件的室内加载变形破坏形态。由图17（a）、（b）可见：在加载初期，试件底部出现数条间距均匀的竖向裂缝，裂缝深度较浅，多位于加载梁下方；弯矩继续增加，原有竖向裂缝深度有所发展，新增竖向裂缝数量有限，但斜向裂缝不断产生和扩展，逐渐向中部延伸，生成水平裂缝；达到极限承载力后，试件变形进一步加剧，多条裂缝从底部扩展到顶部，贯穿了整个截面。

图17 钢筋和钢管格栅混凝土破坏形态Fig. 17 Failure modes of lattice girder concrete and steel tube grid concrete

由图17（c）、（d）可见：在加载初期同样出现几条间距较为均匀的竖向裂缝，裂缝深度浅，主要位于加载梁下方；弯矩进一步提高，原有竖向裂缝深度发展缓慢，新增竖向裂缝数量少，但斜向裂缝数量增长明显，裂缝扩展速度较快；达到极限承载力后，试件破坏明显，多条斜向裂缝从底部两侧逐渐扩展到顶部，形成贯穿裂缝。

3.5 格栅混凝土试件试验结果分析

3.5.1 弯矩–应变曲线

1）钢筋格栅混凝土

图18为钢筋格栅混凝土1/2截面弯矩–应变关系曲线。由图18（a）可见：钢筋格栅混凝土上表面测点CS–1和CS–3表现为拉应变，构件失稳破坏时应变分别为302×10和1 290×10，应力值约为6.9和29.7 MPa；测点CS–2和CS–4表现为压应变，构件失稳破坏时应变分别为–3 449×10和–3 042×10，应力值约为79.3和70.0 MPa；下表面测点CS–9始终承受压应力，构件失稳破坏时应变为–264×10，应力值约为6.1 MPa，测点CS–11起初表现为压应变，随后转变为拉应变，最大拉应变为251×10，应力值约为5.8 MPa；测点CS–10和CS–12表现为拉应变，最终应变值分别为1 007×10和1 020×10，应力值约为23.2和23.5 MPa。

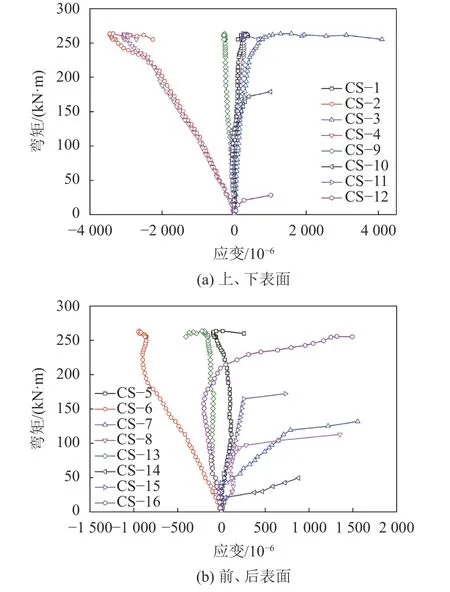
图18 钢筋格栅混凝土1/2截面弯矩–应变关系曲线Fig. 18 Bending moment-strain relationship curves of 1/2 section of lattice girder concrete

由图18（b）可见：钢筋格栅混凝土前表面测点CS–5出现拉、压应力状态的转换，但应变值较小，测点CS–7表现为拉应变，构件失稳破坏时应变为1 557×10，应力值约为35.8 MPa；测点CS-6表现为压应变，构件失稳破坏时应变为-936×10，应力值约为21.5 MPa，测点CS–8表现为拉应变，最大应变为1 351×10，应力值约为31.1 MPa；后表面测点CS–13表现为压应变，构件失稳破坏时应变为–197×10，应力值约为4.5 MPa，测点CS–15表现为拉应变，最大应变为731×10，应力值约为16.8 MPa；测点CS–14表现为拉应变，最大应变为879×10，应力值约为20.2 MPa，测点CS–16起初表现为压应变，随后转变为拉应变，最大拉应变为1 493×10，应力值约为34.3 MPa。

图19为钢筋格栅混凝土1/4 截面弯矩–应变关系曲线。

图19 钢筋格栅混凝土1/4截面弯矩–应变关系曲线Fig. 19 Bending moment-strain relationship curves of 1/4 section of lattice girder concrete

由图19（a）可见：钢筋格栅混凝土上表面测点CS–1开始表现为拉应变，后转变为压应变，构件失稳破坏时应变为–220×10，应力值约为5.1 MPa；测点CS–3表现为拉应变，构件失稳破坏时应变为339×10，应力值约为7.8 MPa；测点CS–2和测点CS–4开始呈现为受压状态，随着荷载不断提高，构件变形不断加剧，逐渐转变为受拉状态，监测到二者的应变值范围为–533×10～445×10。钢筋格栅混凝土下表面测点CS–9承受压应力，构件失稳破坏时应变为–114×10，应力值约为2.6 MPa，测点CS–11表现为拉应变，最大拉应变为516×10，应力值约为11.9 MPa；测点CS–10和测点CS–12起初表现为拉应变，随后转变为压应变，构件失稳破坏时应变分别为–131×10和–84×10。

由图19（b）可见：钢筋格栅混凝土前表面测点CS–5和测点CS–7均表现为拉应变，最大应变值分别为3 135×10和1 622×10；测点CS–6表现为压应变，构件失稳破坏时应变为–335×10，应力值约为7.7 MPa，测点CS–8表现为拉应变，构件失稳破坏时应变为249×10，应力值约为5.7 MPa；钢筋格栅混凝土后表面测点CS–13和测点CS–15表现为拉应变，最大应变分别为3 240×10和338×10，应力值约为74.5和7.8 MPa；测点CS–14起初表现为拉应变，随后转变为压应变，构件失稳破坏时应变为–342×10，应力值约为7.9 MPa，测点CS–16，压应变为–172×10，应力值约为4.0 MPa。

2）钢管格栅混凝土

图20为钢管格栅混凝土1/2截面弯矩–应变关系曲线。

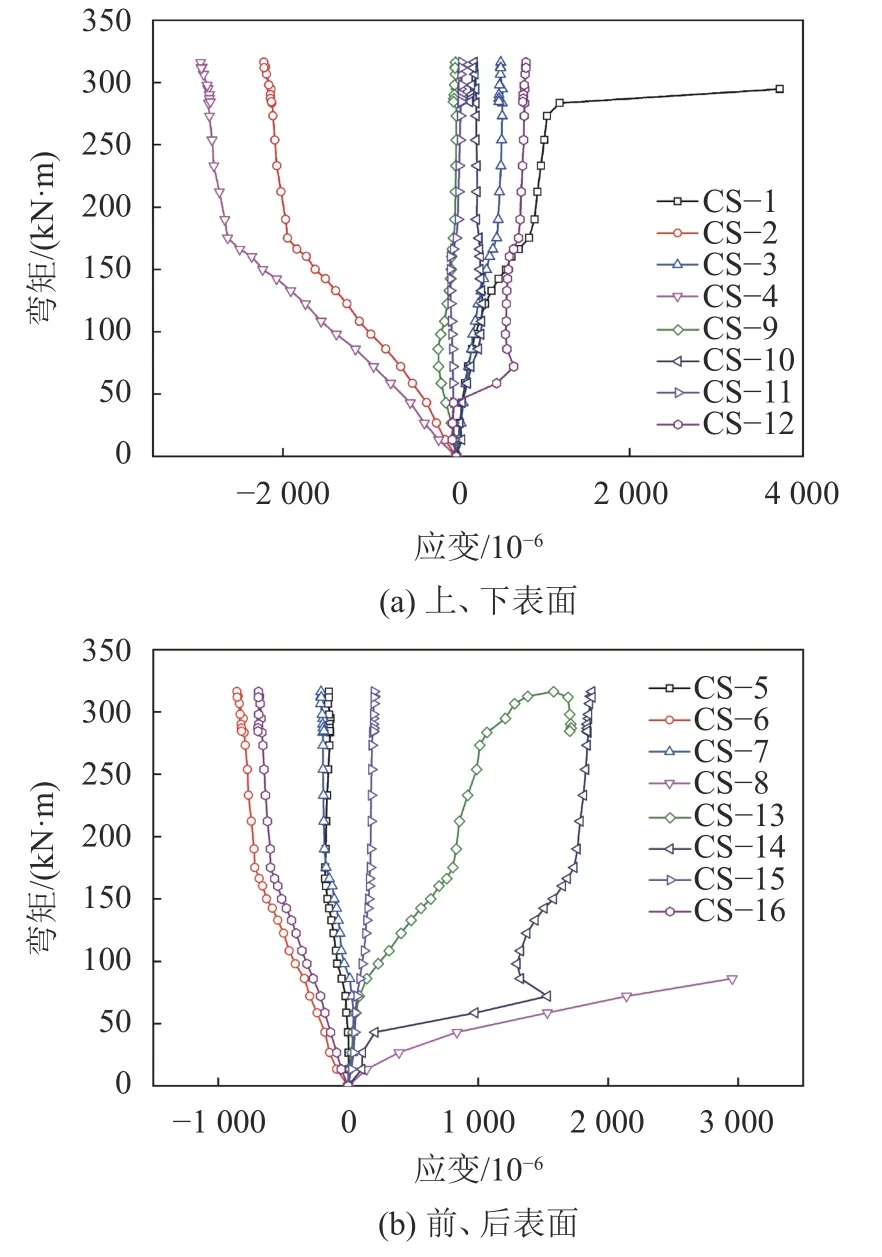
图20 钢管格栅混凝土1/2截面弯矩–应变关系曲线Fig. 20 Bending moment-strain relationship curves of 1/2 section of steel tube grid concrete

由图20（a）可见：钢管格栅混凝土上表面测点CS–1和CS–3表现为拉应变，构件失稳破坏时应变分别为1 194×10和514×10，应力值约为27.5和11.8 MPa，已超过混凝土的极限抗拉强度；而上表面测点CS–2和CS–4表现为明显的压应变，构件失稳破坏时应变分别为–2 219×10和–2 949×10，应力值约为51.0和67.8 MPa，同样已超过混凝土的极限抗压强度；钢管格栅混凝土下表面各测点主要表现为拉应力，最大拉应变发生在测点CS–12，为804×10，应力值约为18.5 MPa。

由图20（b）可见：钢管格栅混凝土前表面测点CS–5和CS–6表现为压应变，构件失稳破坏时应变分别为–148×10和–855×10，应力值约为3.4和19.7 MPa；测点CS–7出现拉、压应变的转换，但应变值较小，最大压应变为–209×10，应力值约为4.8 MPa，测点CS–8表现为拉应变，在加载初期应变就达到2 955×10，应力值约为68.0 MPa；后表面测点CS–13、CS–14和CS–15均表现为拉应变，构件失稳破坏时应变分别为1 581×10、1 875×10和200×10，相对应的应力值约为36.4、43.1和4.6 MPa；测点CS–16表现为压应变，构件失稳破坏时应变为689×10，应力值约为15.8 MPa。

图21为钢管格栅混凝土1/4截面弯矩–应变关系曲线。

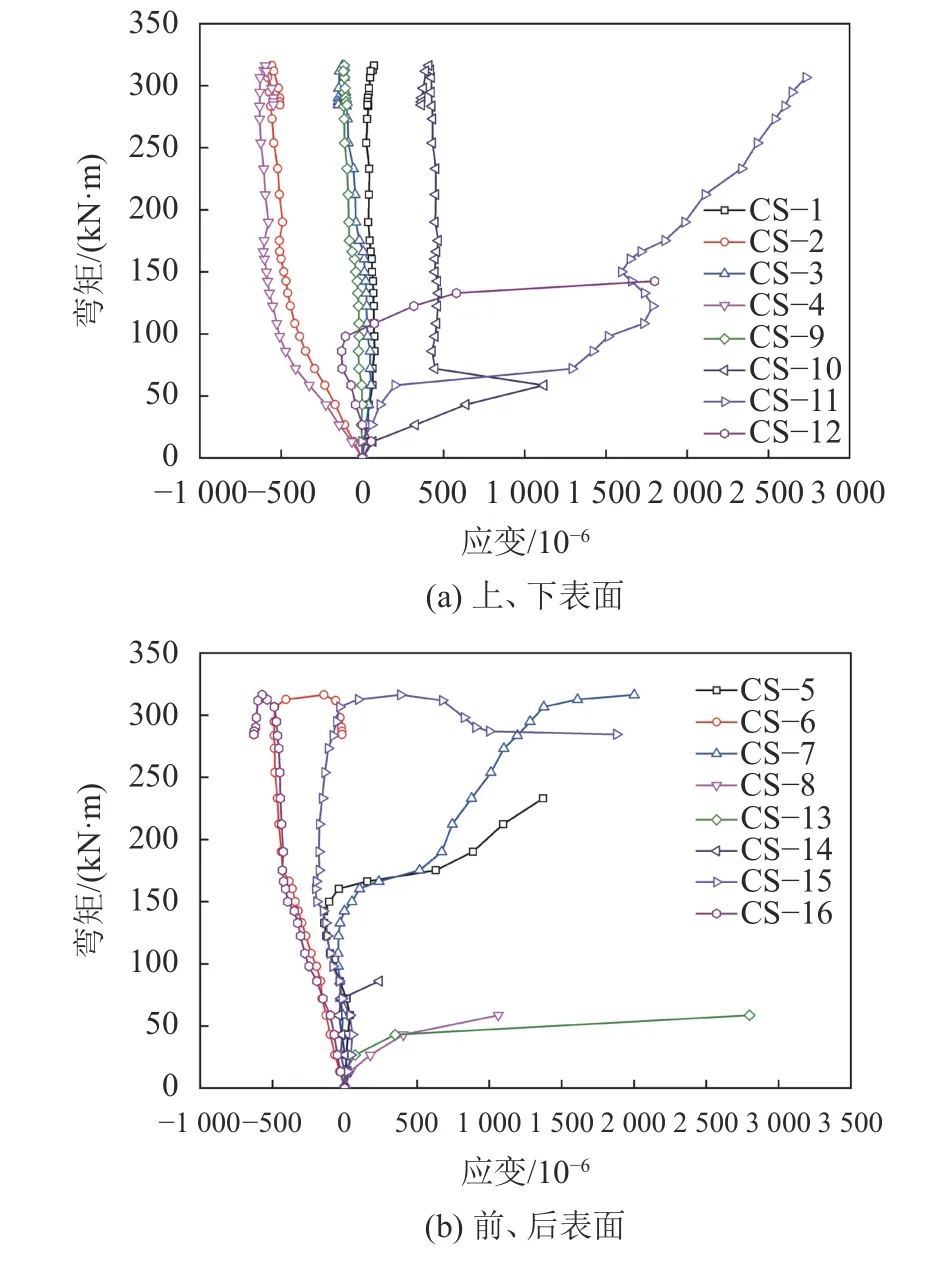
图21 钢管格栅混凝土1/4截面弯矩–应变关系曲线Fig. 21 Bending moment-strain relationship curves of 1/4 section of steel tube grid concrete

由图21（a）可见：钢管格栅混凝土上表面测点CS–1表现为拉应变，最大应变为73×10，应力值约为1.7 MPa；测点CS–2和CS–4表现出明显的受压状态，构件失稳破坏时应变分别为–557×10和–596×10，应力值约为12.8和13.7 MPa；测点CS–3起初表现为拉应变，随后转变为压应变，构件失稳破坏时应变为–141×10，应力值约为3.2 MPa。钢管格栅混凝土下表面测点CS–9表现为压应变，最大压应变为–117×10，应力值约为3.2 MPa；测点CS–10表现为拉应变，构件失稳破坏时应变为421×10，应力值约为9.7 MPa；测点CS–11和CS–12表现出明显的受拉状态，测得的最大拉应变分别为2 731×10和1 800×10，应力值约为62.8和41.4 MPa。

由图21（b）可见：钢管格栅混凝土前表面测点CS–5和CS–7在加载前期表现为受压状态，后期转变为受拉状态，测得的最大拉应变分别为1 373×10和2 002×10，应力值约为31.6和46.0 MPa；测点CS–6表现为受压状态，构件失稳破坏时压应变为–406×10，应力值约为9.3 MPa；测点CS–8在加载前期表现为受拉状态，随后测点失效，测得的最大拉应变为1 062×10，应力值约为24.4 MPa；钢管格栅混凝土后表面测点CS–13在加载初期应变就达到2 800×10，应力值约为64.4 MPa；测点CS–15在加载前期表现为受压状态，后期转变为受拉状态，构件失稳破坏时应变为676×10，应力值约为15.5 MPa；测点CS–16表现为受压状态，构件失稳破坏时应变为–601×10，应力值约为13.8 MPa。

3.5.2 弯矩–挠度曲线

图22为钢筋格栅混凝土试件和钢管格栅混凝土试件的弯矩–挠度曲线对比。由图22可见：加载初期，2种试件均处于弹性变形阶段，挠度随弯矩呈线性增加，二者的挠度增长速率基本一致；弯矩继续施加，挠度增长速率渐渐提高，钢筋格栅混凝土的变形幅度较大；达到极限承载力后，钢管格栅混凝土的承载力出现明显下降，最终仍维持在较高水平。钢筋格栅混凝土试件达到极限承载状态时的跨中挠度约为45.8 mm，极限承载力为258.3 kN·m, 而钢管格栅混凝土达到极限承载状态时的跨中挠度约为47.8 mm，极限承载力为316.3 kN·m，较钢筋格栅提高了22.5%，表明，钢管格栅混凝土具有较高的承载能力和较好的抗变形能力。

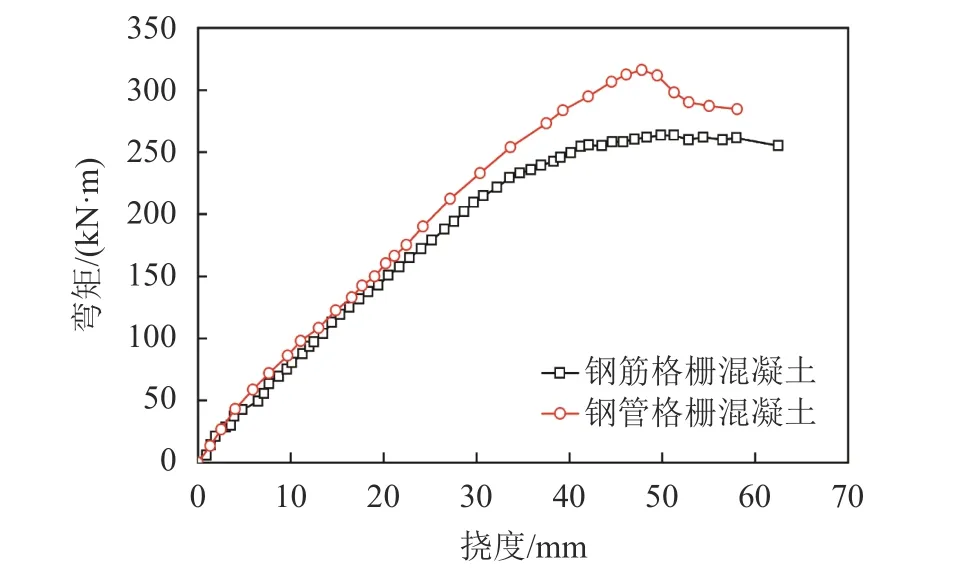
图22 钢筋格栅混凝土和钢管格栅混凝土弯矩–位移关系曲线对比Fig. 22 Bending moment-deflection relationship curves of lattice girder concrete and steel tube grid concrete

4 结 论

通过室内模型试验，对新型钢管格栅拱架用作隧道初期支护的承载特性进行了研究，对比分析了钢筋格栅和钢管格栅的变形特征、破坏形态及应力应变规律，主要结论如下：

1）钢筋格栅表现出折线形压弯破坏，主肢钢筋处于较高的应力应变状态，π形筋变形显著，卸载后回弹变形量较小；钢管格栅表现为平滑曲线形破坏，π形筋变形明显，应力值较高，卸载后回弹变形量较大。

2）钢管格栅的极限承载力为96.6 kN·m，相当于钢筋格栅的1.8倍，并且，其最大允许变形量达55.1 mm，约为钢筋格栅的1.6倍，验证了钢管格栅高强度高韧性的特点。

3）钢筋格栅混凝土试件竖向裂缝深度较发育，多条裂缝从底部逐渐扩展到顶部，贯穿了整个截面，斜向裂缝不断产生和扩展，并形成多条水平裂缝；钢管格栅混凝土试件竖向裂缝深度较浅，加载后期斜向裂缝数量增长明显，裂缝扩展速度较快，多条斜向裂缝从底部两侧逐渐延伸到顶部，形成贯穿裂缝。

4）钢筋格栅混凝土试件最大允许变形量为45.8 mm，极限承载力为258.3 kN·m；而钢管格栅混凝土试件最大允许变形量为47.8 mm，极限承载力为316.3 kN·m，承载力较钢筋格栅提高了22.5%，体现出钢管格栅混凝土较高的承载能力和较好的抗变形能力。

综上分析，高强钢管格栅支护结构具有优异的受力性能，为隧道初期支护提供了一种新方法，对软弱破碎、早期变形速度快的围岩条件或隧道洞口、联络通道等地段具有较好的潜在推广价值。但文中未对钢管格栅和钢筋格栅与混凝土的黏结性能差异展开详细讨论，由于试验条件的单一性和在实际隧道工程使用条件的复杂性，高强钢管格栅的支护特性及适用范围还有待进一步工程验证。