二维桥式吊车自适应神经网络消摆控制①
2022-07-26何熊熊王逸文朱铮旸
何熊熊 王逸文 朱铮旸 陈 强
(浙江工业大学信息工程学院 杭州 310023)
0 引言
吊车是用来运输超出人类自身能力范围的负载的设备,被广泛用于不同的环境作业,例如建筑工地、仓库、码头等[1]。其中,桥式吊车是一类典型的欠驱动机械系统,实际运行中受各种外界干扰的影响,其负载容易发生大幅摆动,导致系统工作效率降低,甚至带来一定的安全隐患。因此,如何实现吊车的消摆控制和台车的快速、准确定位,是吊车控制器设计中的热点问题之一。
近年来,国内外学者提出多种控制方法实现欠驱动桥式吊车的有效消摆控制,主要分为开环控制和闭环控制。其中,开环控制代表性方法有输入整形[2]、轨迹规划[3-5]等。相比开环控制系统,闭环控制鲁棒性更强,适用于室外作业的吊车控制器设计。常见的代表性闭环控制的方法主要包括比例积分微分(proportion integration differentiation,PID) 控制[6-7]、最优控制[8-9]、滑模控制[10-12]等。文献[13]提出一种新的滑模控制方法,通过对系统模型进行变换并构建新的滑模面,保证系统状态沿滑模面收敛到零。文献[14]同时考虑系统匹配和非匹配干扰,设计扰动观测器估计和补偿未知干扰,并设计滑模控制器提高系统鲁棒性。
文献[15]针对一类欠驱动吊车系统,通过设计滑模微分器保证控制输入信号及其导数的连续性,从而减小控制输入的抖振问题。文献[16]针对二维桥式吊车提出一种基于无源性方法通过构造具有所需阻尼特性的新储能函数引入耦合耗散信号以显著降低负载摆动,并基于Lyapunov 稳定性和LaSalle不变性原理设计控制器并证明闭环系统的稳定性。
上述文献尽管可以实现桥式吊车的有效消摆控制,但控制器设计多依赖于较为精确的吊车系统模型。在实际系统中,由于存在未建模的动力学动态以及参数不确定性,吊车实际系统与其理论模型之间通常存在一定的差异。文献[17]从系统无源性的角度出发,针对二维吊车系统中存在未知质量、未知绳长及摩擦力等问题,设计相应的自适应控制器,但要求未知不确定参数满足线性参数化条件。为提高模型不确定系统的控制性能,模糊控制[18-19]、神经网络[20-22]等人工智能策略被广泛应用于控制器设计中。文献[23]针对不确定二维桥式吊车系统,利用多个误差变量构造滑模面和设计自适应模糊滑模控制,并利用模糊机制改变滑模面的梯度。文献[24]将PID 控制与神经网络补偿相结合设计吊车控制器,不仅能减小负载摆幅,还可补偿重力、摩擦力等未知因素的影响。文献[25]针对二维桥式吊车,利用神经网络逼近滑模控制器中各个参数,实现台车精确定位以及负载摆动有效消除。然而,现有的吊车神经网络控制方法一般需要在控制器设计时将系统模型在平衡点处进行线性化处理,导致系统在偏离平衡点时,负载需要多次震荡才能消除摆动。
基于上述讨论,本文提出一种不依赖于精确模型的自适应神经网络滑模控制策略。通过模型变换,构造包含台车位移和摆角的误差及导数的滑模面,并设计相应的滑模控制器和自适应律,保证当滑模变量收敛至平衡点时,各误差信号均收敛到零点,从而达到台车位置控制和负载消摆的目的。此外,利用神经网络逼近吊车系统中的非线性不确定,使得控制器设计中无需台车、负载质量信息或对系统模型进行线性化处理。最后,利用Lyapunov 稳定性理论分析闭环系统信号的有界性和误差收敛性,并搭建二维桥式吊车实验平台验证本文所提方法的有效性。
1 问题描述
二维桥式吊车模型如图1 所示,其动态特性可用如下方程描述[13]:
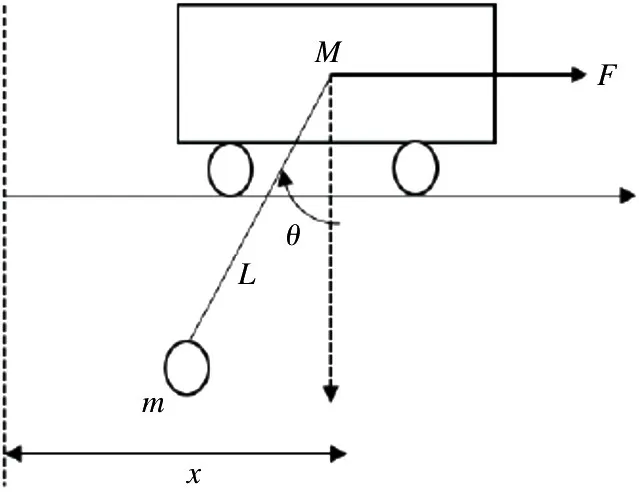
图1 二维桥式吊车模型
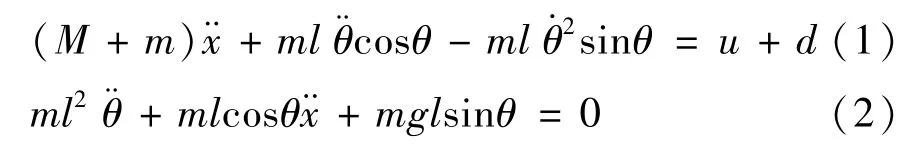
其中,x表示小车位移,θ表示摆角幅度,表示摆角速度,表示摆角加速度,M表示小车质量,m表示负载的质量,u表示控制输入,d表示包括电磁干扰和风力干扰等在内的有界干扰,满足|d(t)|<,其中>0 表示干扰上界。
定义吊车的期望轨迹xd,其具体表达式为xd=0.605(1-)。为便于控制器设计,进行以下模型变换,定义下列状态变量:
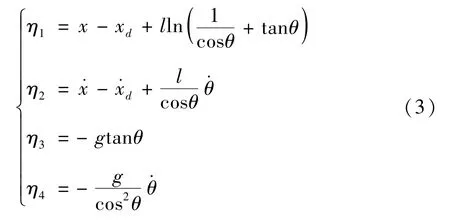
对式(3)求导可得
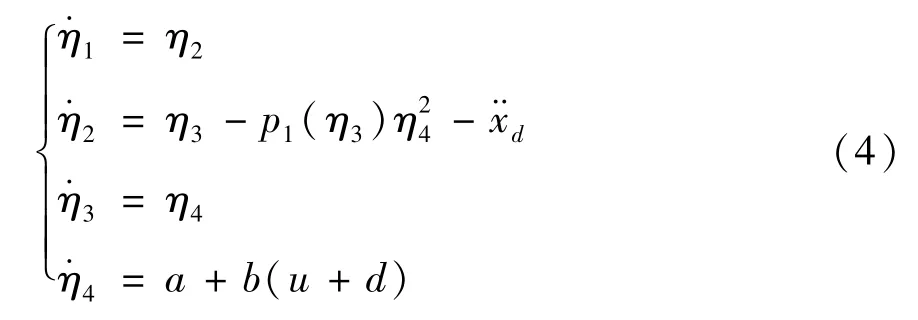
其中,
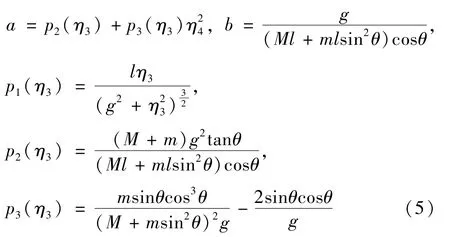
本文控制目标是针对式(1)和(2)所示的二维桥式吊车系统,设计自适应神经网络控制器,使得式(3)中状态变量η1、η2、η3和η4最终均趋于零点。
注1在实际状况中,由于绳子质量远小于台车质量,绳子的韧性可以忽略。因此,在描述二维桥式吊车时可以将绳视为刚性。此外,负载被视为质点并且它的质量是均匀的。
注2在二维桥式吊车中,负载摆角θ(t) 通常在(-π/3,π/3)内。结合式(4)可知,b存在上界和下界,即0<b0≤b≤b1,其中b1和b0分别表示其上、下界值。
2 神经网络消摆控制
二维桥式吊车神经网络控制结构图如图2 所示,其中控制器采用滑模控制,神经网络用于估计包含未建模动态和不确定参数在内的非线性不确定性。
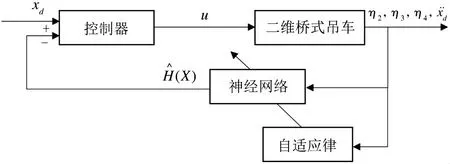
图2 二维桥式吊车神经网络控制结构图
2.1 控制器设计
本文设计的滑模面形式如下:
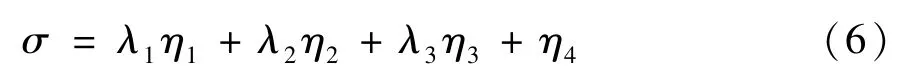
对σ求导可得:
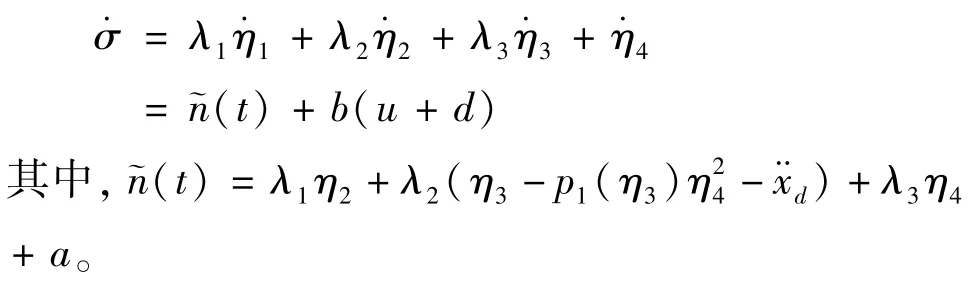
由于神经网络能够逼近任意连续函数,因此利用H(X) 来逼近非线性函数˜n(t)。其中,H(X) 表达式为
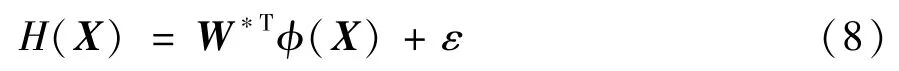
X=∈R4表示神经网络输入向量,ϕ(X) 表示神经网络(neural network,NN)基函数,具体表达式为
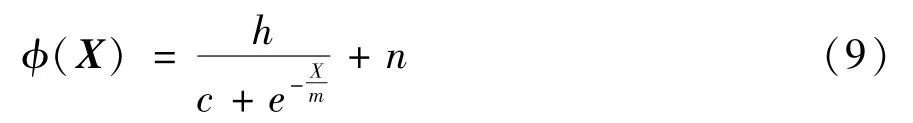
其中,W*=[w1,w2,w3,w4]T∈RN和ε分别表示理想有界的权值矩阵和神经网络逼近误差,h、c、m、n为常数,且‖W*‖≤WN,|ε|≤εN,WN为‖W*‖的上界,εN为ε的上界,WN>0,εN>0。为了后续设计中表达方便,将ϕ(X) 记为ϕ。
结合式(6)~(10),设计控制器为
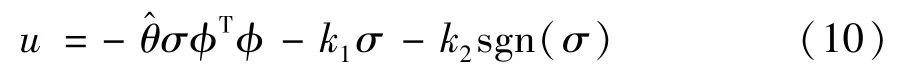
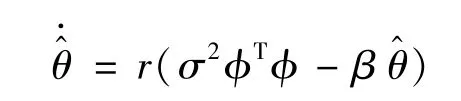
其中,r>0,β>0。
注3控制器式(9)中的符号函数sgn(·)会带来一定的控制器抖振问题,因此在实验中将采用以下连续函数[26]代替sgn 函数。
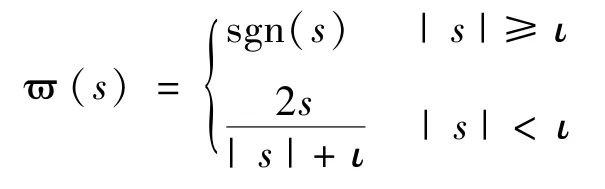
其中,ι>0 表示边界层厚度。
2.2 收敛性分析
定理1针对式(1)和(2)所示的二维桥式吊车系统,选择滑模面式(6),且设置控制律式(10)中的参数满足k1>0,k2≥+(‖W*Tϕ(X)‖F+|εN|)/b0,则当t→∞时,滑模变量σ收敛至滑模面σ=0。
证明由式(9)可得:
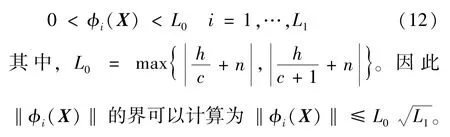
构造如下Lyapunov 函数:

对式(13)求导,并将式(7)和式(10)代入可得
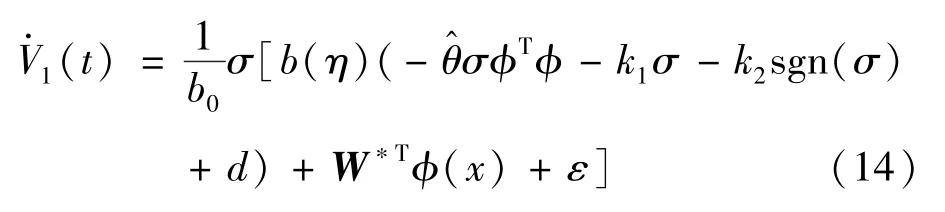
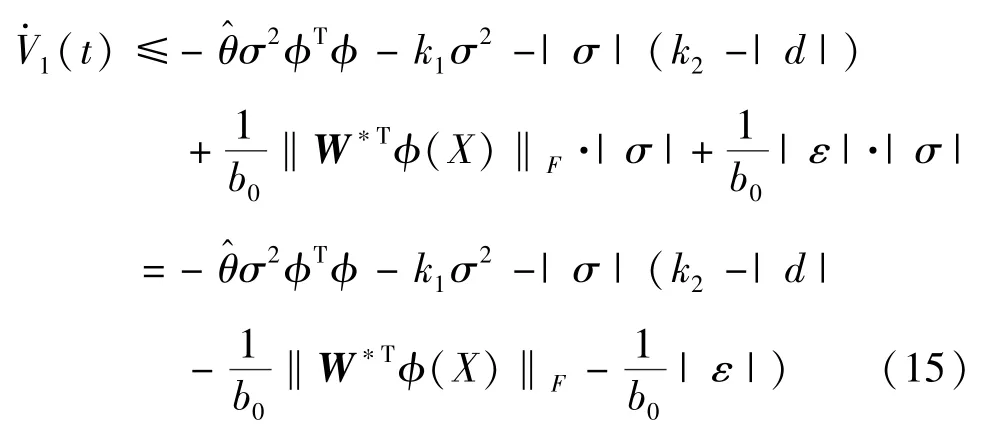
由于d(t)<||、‖W*Tϕ(X)‖F、ε均有界,因此选择k2≥+(‖W*Tϕ(X)‖F+|εN|)/b0,将不等式代入到式(15)可得:
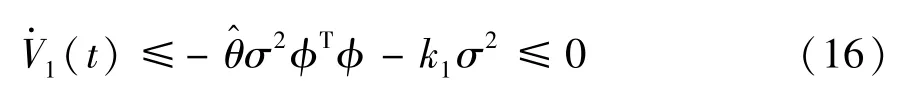
定理2当滑模变量σ收敛至滑模面σ=0 时,各个状态变量η1、η2、η3、η4最终均趋于零点。
证明当滑模变量σ收敛至滑模面σ=0 时,根据式(6)可得:
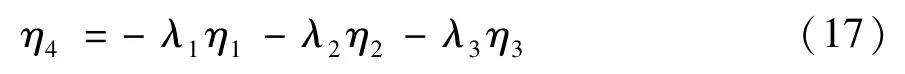
将式(17)代入式(4)可得:
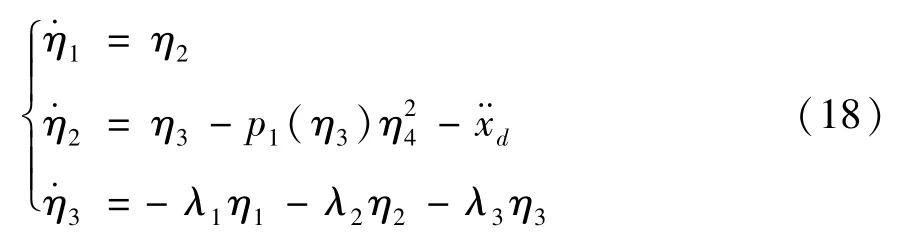
为便于后续分析,将式(18)改写为

根据矩阵理论,存在一个可逆矩阵Γ,使得

其中,J=,k表示A的特征值。不失一般性,选择λ1=k3,λ2=3k2,λ3=3k,可逆矩阵表示为
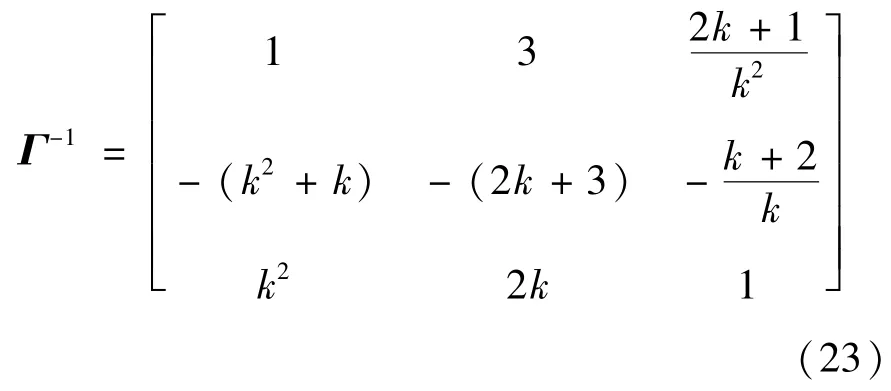
根据式(19)、式(21)和式(23)可得:
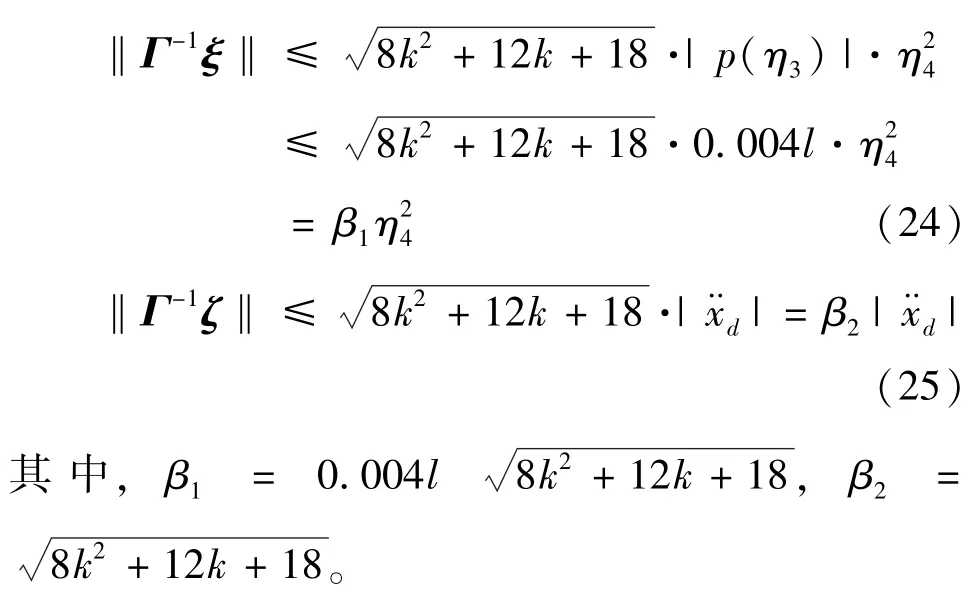
定义式(26)所示的新的状态变量:

根据式(26)可得:

式(17)经过变换可得:
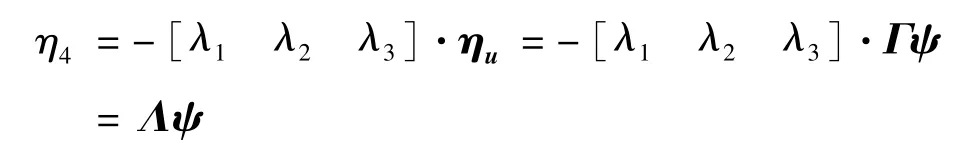
其中,Λ=-[λ1λ2λ3]·Γ。则≤‖Λ‖2·‖ψ‖2,将不等式代入式(24),有
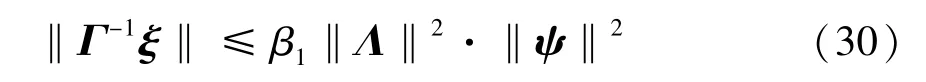
对式(26)求导可得:

将式(19)代入式(31)中可得:
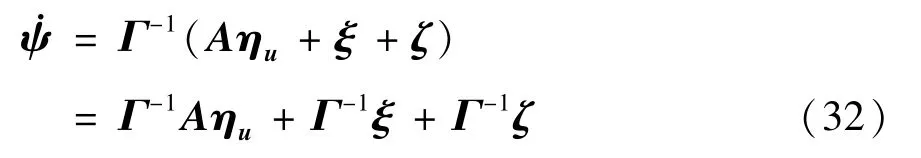
将式(22)和式(27)代入式(32)可得:
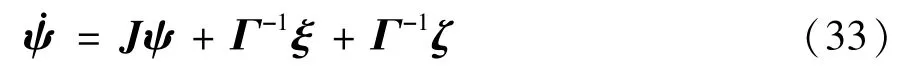
定义如下Lyapunov 函数:

对式(34)求导可得:
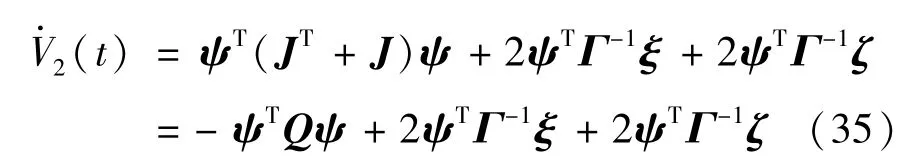
其中,Q=-(JT+J),且Q特征值为2k,2k±。
令k>,则Q的每一个特征值都为正值,且Q的最小特征值为λm=2k-。因此ψTQψ≥λm‖ψ‖2,将不等式代入式(35)可得:
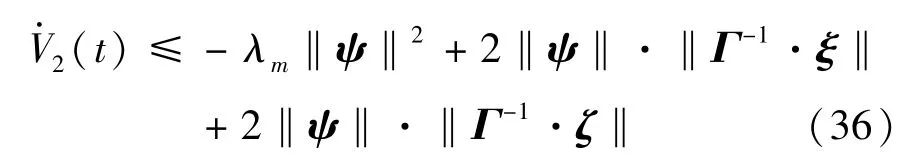
将式(24)和式(30)代入式(36)可得
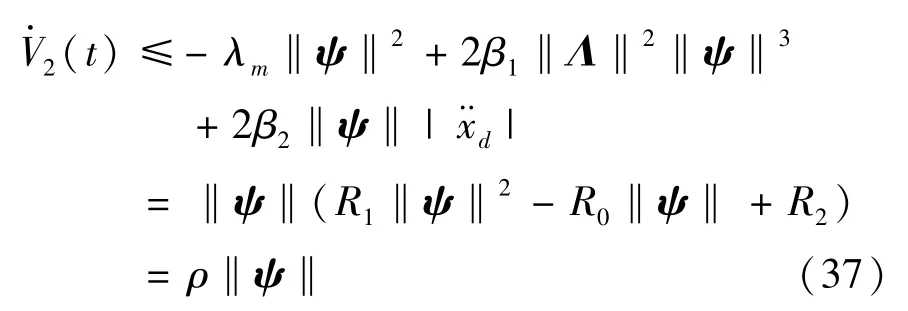
其中,R0=λm,R1=2β1·‖Λ‖2,R2=,ρ=R1‖ψ‖2-R0‖ψ‖+R2。
由于R0>0、R1>0,则存在一个区间使得ρ<0。该区间通过计算可得:

综上所述,当‖ψ‖初值在区间[0,R0/2R1)时有
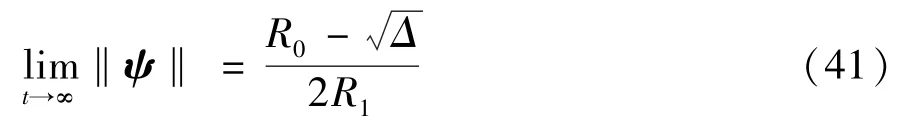

由于ηu=[η1η2η3]T,因此η1、η2、η3将趋于0,再根据式(17)可知,η4将趋于0。证毕。
3 实验分析
为进一步验证本文所提方法的有效性,搭建二维桥式吊车控制系统实验平台,并与不同的控制方法进行对比。其中,方法1 为本文所提出的自适应神经网络控制方法,方法2 为文献[15]所提出的滑模控制方法,其中滑模面和控制器分别设计为
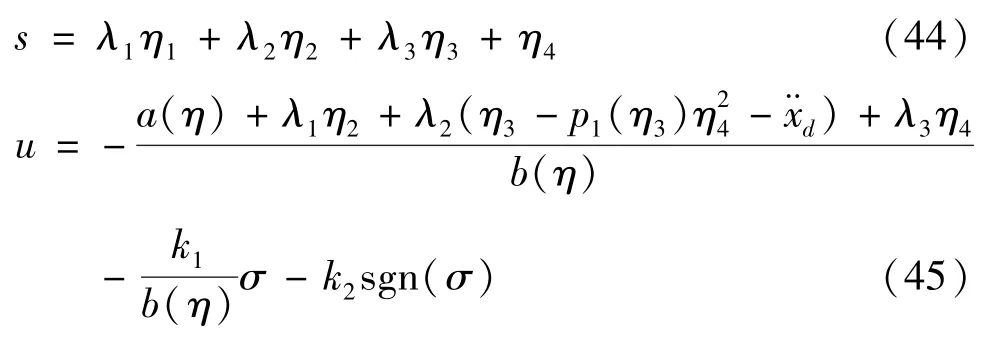
实验平台主要包括个人电脑、伺服驱动器、运动控制板和角度编码器,具体设备如图3 所示。台车的位移由嵌入在伺服电机内的编码器测量,而负载摆角由固定在小车下方的编码器捕获。控制器使用经过低通滤波器后的测量数据在线估算台车以及摆角速度。控制器选用DSP28335 芯片,开关频率设置为50 kHZ,并采用CCS 编译工具编写相关软件程序。
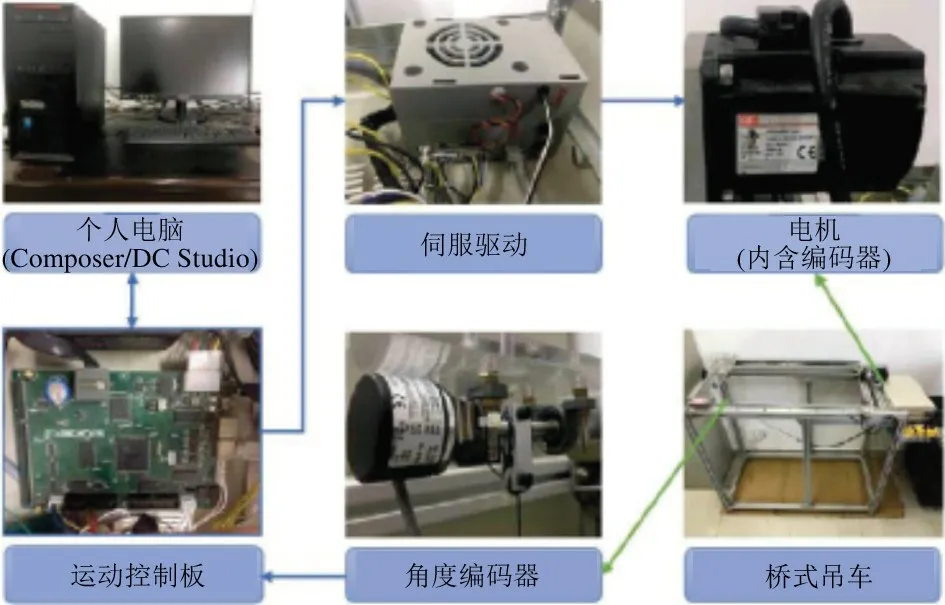
图3 桥式吊车实验系统
桥式吊车平台的物理参数为m=1 kg,M=1.7 kg,l=0.8 m,g=9.8 m/s2。台车参考轨迹为xd=0.605(1-)。在实验中,其他相关参数如表1 所示。

表1 实验控制参数
实验结果如图4~图7 所示,其中图4 描述了台车在方法1 和方法2 的作用下的运行轨迹。由图4可以看出,在方法1 和方法2 控制下系统稳态时均存在一定的稳态误差,但方法1 控制下的稳态误差远小于方法2,且方法1 更早到达系统稳态。图5给出了不同控制方法下负载摆角对比。由图5 可以看出,方法1 和方法2 的最大负摆角为1.08 °和1.18 °,方法1 和方法2 的最大正摆角分别为0.99°和1.08 °。因此,方法1 具有更好的瞬态性能。
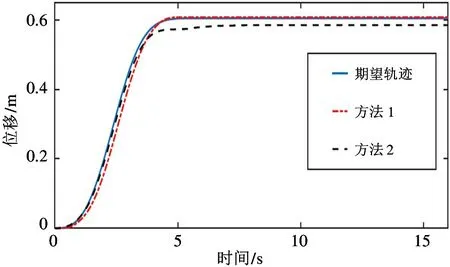
图4 台车位移对比
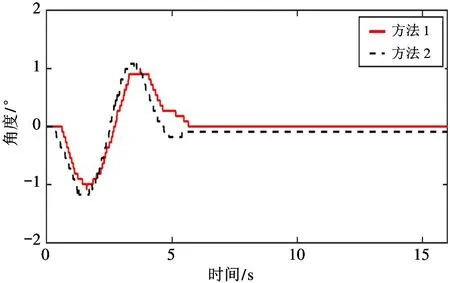
图5 负载摆角对比
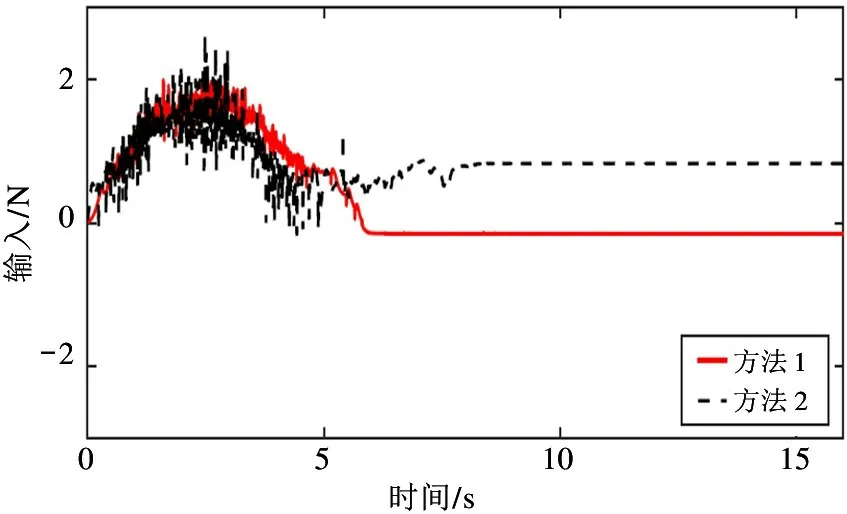
图6 控制输入对比
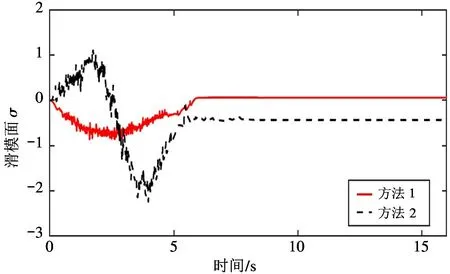
图7 滑模变量σ 对比
图6 给出了方法1 和方法2 的控制输入信号。从图6 中可以看出,方法1 的输入信号比方法2 幅值更小,且能较早趋于稳态。图7 给出了在方法1和方法2 作用下系统滑模面的值。从图7 中可以看出,随着系统的运行,方法1 滑模变量σ的值能够更快收敛至零点附近。表2 给出了两种方法具体的实验性能指标。
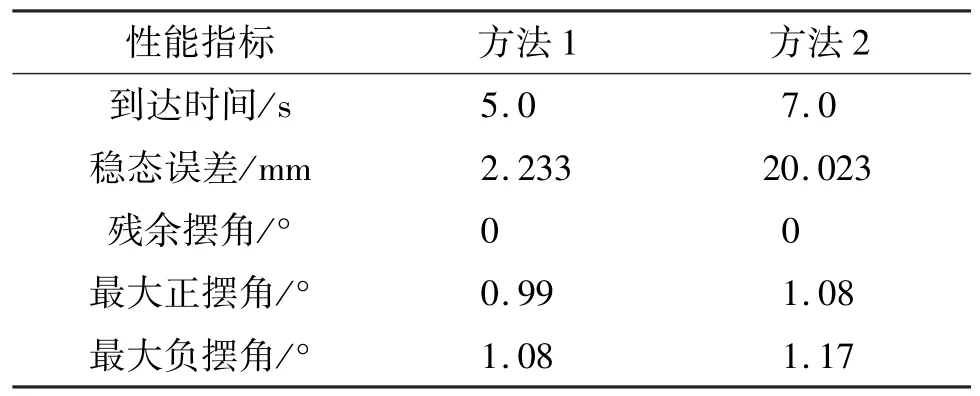
表2 实验性能指标
从表2 中可以看出,方法1 比方法2 在更快时间内到达期望点,且方法1 具有更小的稳态误差,这与图4 描述的结果一致,即方法1 能够提高系统稳态性能。方法1 和方法2 最终均未产生残余摆角,但在运行过程中,方法1 的最大正摆角和最大负摆角均小于方法2。结合图5 与表2 可知,方法1 能够提高系统的动态性能。
4 结论
本文针对二维桥式吊车系统的台车精确定位与负载摆动消除等问题,提出一种自适应神经网络消摆控制方法。通过神经网络逼近系统中的非线性函数,减少控制器对系统模型信息的依赖。同时,通过构造包含台车位置与负载摆角误差在内的滑模变量,将控制器目标转换为保证滑模变量收敛至平衡点,从而使得台车到达期望位置的同时能够消除负载摆动。最后,在实际二维桥式吊车平台上进行了实验验证,实验结果表明本文所提方法的有效性。
