外压和力偶荷载组合作用下含凹陷缺陷海底管道的局部屈曲和极限弯矩承载力

2022-07-26陈严飞侯富恒董绍华贺国晏王春莎

中国石油大学学报（自然科学版） 2022年3期

陈严飞, 侯富恒, 黄俊, 董绍华, 贺国晏, 刘宇, 王春莎

(1.中国石油大学(北京)油气管道输送安全国家工程实验室,北京 102249; 2.大连理工大学工业装备结构分析国家重点实验室,辽宁大连 116024; 3.中海油研究总院,北京 100102)

凹陷作为海底管道常见的失效形式之一,一般由海上落物、落锚等因素使管壁受到碰撞挤压导致[1],会危害海底管道的安全运行。同时,由于海床坍塌、泥石流、沙坡沙脊活动以及海底高静水压等影响往往会使海底管道处于力偶和外压荷载的组合作用下,因此明确含凹陷海底管道在外压和力偶荷载组合作用下的屈曲失效机制,提出相应的完整性评价方法,对维护海底管道的安全运行具有重要意义。对于凹陷海底管道的完整性评价,ASME B31.8[2]和API 579[3]是工业界最常用的规范,但这些规范给出的方法仅适用于内压占主导作用下的陆上管道。Toscano等[4]考虑了载荷加载路径的影响,研究了管道在力偶和外压共同作用下的极限弯矩承载力,并进行了相关的试验研究。付光明等[5]建立有限元模型,考虑初始椭圆度的影响,研究筛管在外压与弯矩复合荷载下的失效规律,并提出压溃荷载计算公式。马善洲等[6]基于平面弹性梁理论,研究了纯弯作用下圆柱钻杆的最大弯曲应力,认为钻杆接头对弯曲应力有明显影响。Cai等[7-8]建立完整管道的有限元数值模型,研究了结构损伤对无缝金属管剩余极限强度的影响。Kyriakides等[9]分别采用试验和数值模拟研究了管道在弯曲作用下的屈曲失效机制。Pournara等[10]采用试验与数值模拟方法研究管道分别在循环弯曲荷载和循环压力荷载下的失效模式,并提出了凹陷管道剩余强度的评估方法。Bai等[11]使用有限元方法建立不同径厚比的管道数值模型,得到外压和力偶联合作用下管道的极限荷载预测方法。余建星等[12-13]分别针对完好和含初始椭圆度的海底管道进行了全尺寸压溃试验和数值模拟得到管道凹陷深度的变化规律。Gong等[14]考虑了初始椭圆度的影响,采用小尺寸模型试验、理论分析和数值仿真相结合的方法研究了外压作用下海底管道局部屈曲机制和极限弯矩承载力。叶皓等[15]对海底管道在单一和组合荷载作用下的局部屈曲失效研究成果进行了整理,并提出了安全评价方法。综上所述,虽然迄今为止国内外学者针对海底管道的局部屈曲问题开展了一系列研究,但大部分研究都是针对无缺陷的完好管道和单一的荷载形式,对外压和力偶荷载组合作用下凹陷海底管道的局部屈曲研究相对较少,也缺乏相应的完整性评价方法。笔者针对外压和力偶组合作用下含凹陷管道的局部屈曲失效开展研究,探究组合荷载对海底管道局部屈曲失效的影响规律,确定凹陷深度、外压、径厚比等参数对管道极限弯矩承载力的影响规律,提出外压和力偶组合荷载作用下凹陷海底管道极限承载力计算方法。

1 有限元数值模型

1.1 有限元模型建立

如图1所示,采用3D壳单元建立管道模型,并采用球形压头制造管道凹陷。管道与凹陷具有对称性,因此建立1/2管道模型。管道模型的长度L为3 180 mm,外径D为318 mm,屈服强度σy为415 MPa,泊松比ε为0.3,弹性模量E为209 GPa,径厚比D/t分别选取18.9、24.2、29.2、35、40和60,其中t为管道壁厚,mm。将管道中心截面的边界条件设置为对称约束模拟完整管道,在管道末端圆心设置一个参考点,将参考点与管道末端截面进行MPC绑定约束,使管道末端截面各个节点的自由度与参考点的自由度进行耦合,便于加载弯曲力偶荷载,并将参考点边界条件设置为轴向自由,其他自由度为0,允许模型有轴向的自由度,防止产生多余的轴力。

图1 管道有限元模型

海底管道受到外部高静水压力,外压远大于内压,在计算时二者会相互抵消,同时基于对海底管道最危险工况的考虑,即管道没有运行,内压为零,因此不引入内压这一参数。施加的荷载为作用在管道外表面的外压与管道端部参考点处的弯曲力偶M,在力偶作用下,管道会发生弯曲,进而使管道受到弯矩作用。在最危险工况下,凹陷的环向位置设置在管道在力偶作用下产生弯曲时的受压侧,轴向位置在管道的中间处。

数值模拟过程可分为4个分析步:①利用球形压头在管道顶部制造凹陷缺陷;②移除球形压头和下方挡板;③在管道外表面加载静水压力以模拟海底环境;④采用弧长法在管道端部加载弯曲力偶荷载,直至屈曲失效,得到管道的极限弯矩承载力。数值模拟中选择API X60钢材,其应力应变曲线如图2[16-17]所示。

图2 X60钢材应力-应变曲线

1.2 模型有效性验证

Park等[18]建立实际管道模型,采用试验方法得到不同凹陷深度下管道的压溃压力。采用本研究建立的有限元数值模型计算含凹陷海底管道的压溃压力,为了与试验模型一致,在计算时不考虑力偶荷载并保持原有的边界条件不变,验证所用的管材屈服应力与试验管材保持一致。将数值模拟计算得到的压溃压力与试验值进行对比,对比结果如表1所示。由表1可知,数值模拟值与试验值吻合较好,表明建立的有限元模型可以给出较准确的计算结果。

表1 数值模拟与试验结果对比

2 组合荷载作用下凹陷海底管道局部屈曲失效模式

通过数值模拟发现管道从凹陷形成到屈曲失效可以分为5个阶段:第一阶段,如图3(a)、4(a)所示,管道处于未加载阶段,为无缺陷完好管道;第二阶段,如图3(b)、4(b)所示,管道处于凹陷形成阶段,压头在管道12点位置形成凹陷缺陷,管道椭圆度发生明显变化;第三阶段,如图3(c)、4(c)所示,管道处于加载外压阶段,在凹陷海底管道外表面加载固定外压,管道凹陷深度略有增大,管道局部变形不明显;第四阶段,如图3(d)、4(d)所示,加载力偶荷载直至管道发生屈曲失效,管道局部变形有一定增大,但管道的弯曲程度不明显;第五阶段,如图3(e)、4(e)所示,管道处于后屈曲阶段,在管道达到临界屈曲状态之后,管道发生失稳破坏,局部发生较大变形,管道的弯曲程度较为明显。

图3 管道中心截面变形

图4 不同力偶作用下管道变形示意图

3 有限元数值模拟结果

3.1 外压对管道局部屈曲和极限弯矩承载力影响

如图5所示,外压会对凹陷管道的极限弯矩承载力产生影响,图中每条曲线的最高点即为该外压作用下凹陷管道的极限弯矩承载力,随着外压增大管道的极限弯矩承载力逐渐降低。在管道未达到屈曲状态时,随着弯矩增大管道凹陷最低点的位移没有显著变化,说明管道局部变形较小;当加载的力偶使管道达到极限弯矩承载力之后,管道发生屈服,弯矩迅速减小,而管道凹陷最低点位移迅速增加,说明管道达到屈服状态之后,即使施加较小力偶也会发生较大的变形。

图5 加载的力偶与管道凹陷最低点位移关系

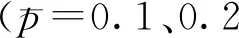
图6 外压对管道失效模式影响

基于给定的管道径厚比,在凹陷深度δ一定的情况下,随着外压增大,管道的极限弯矩逐渐减小。如图7(a)、(b)所示,在径厚比较小时,完整管道与浅凹陷管道(δ/D为0和0.04)的极限弯矩承载力(无量纲)几乎相等,随着径厚比增大,管壁变薄,极限弯矩承载力差值变大。如图7所示,对于径厚比相对较小的管道(D/t=18.9、24.2、29.2、35和40),加载的外压荷载越大,管道的极限弯矩承载力减小的越快,而且凹陷深度越大,外压对极限弯矩承载力的削弱作用越明显。

图7 不同径厚比下管道外压对凹陷管道极限弯矩承载力的影响

3.2 凹陷深度对管道局部屈曲和极限弯矩承载力影响

如图8所示,将管道屈曲失效时凹陷处附近的应变进行对比,可以看出,凹陷管道在力偶荷载作用下达到局部屈曲时,在凹陷中心处产生较大的压应变,而在凹陷的两侧则会产生较大拉应变,在远离凹陷的区域,管道应变几乎为0。对于凹陷深度大的工况,凹陷两侧的拉应变较大,并且向凹陷两侧扩展范围也较大,此时失效模式更明显。

图8 管道屈曲时凹陷附近的应变

如图9所示,含凹陷管道的极限弯矩承载力(无量纲)比完整管道要小,在基于给定的管道径厚比(D/t=18.9、24.2、29.2、35、40和60)下,随着凹陷深度增加,管道的无量纲极限弯矩逐渐减小,抗弯能力降低。管道径厚比较小时(D/t=18.9和24.2),如图9(a)、(b)所示,凹陷对管道极限弯矩承载力的影响不够明显,因此完整管道与凹陷深度较浅管道(δ/D=0.04)的极限弯矩相差很小;当凹陷深度继续增大(δ/D>0.04)时,影响逐渐明显,管道极限弯矩承载力呈线性下降。如图9(c)、(d)、(e)所示,当管道径厚比增大时,管壁变薄,浅凹陷管道的极限弯矩承载力下降比较明显。当管道径厚比足够大(D/t=60)时,反而凹陷较浅时极限弯矩降低较快,这是因为管壁很薄,凹陷一旦出现就极大地破坏了管道的完整性,使管道的极限弯矩明显下降。因此对于厚壁管道来说,浅凹陷对管道极限弯矩承载力影响不大;而对于薄壁管道来说,浅凹陷对管道的极限弯矩承载力会有较大影响,需要采取相应措施防止管道失效。