基于管单元的水平井多簇压裂有限元模拟方法
2022-07-26李明辉周福建黄国鹏胡晓东李浩哲
李明辉, 周福建, 黄国鹏, 王 博, 胡晓东, 李浩哲
(1.中国石油大学(北京)油气资源与探测国家重点实验室,北京 102249; 2.中国石油大学(北京)克拉玛依校区石油学院,新疆克拉玛依 834000; 3.中煤科工集团西安研究院有限公司,陕西西安 710077)
为促进水平井多簇裂缝的同时起裂与扩展,现场常采用限流法或暂堵法压裂工艺[1-4]。限流法压裂工艺的核心是增大水平井筒内射孔摩阻,限制各簇裂缝的进液能力,从而促使多缝同时起裂与扩展[5]。然而现场分布式光纤[6]表明多缝扩展并不均匀,同时井下摄像机[7]显示携砂液会不断冲蚀射孔,造成限流失效,这表明射孔冲蚀现象对限流法压裂的影响不可忽略。暂堵法压裂是另一种实现多缝均匀扩展的现场工艺[8]。在压裂过程中,暂堵剂随压裂液进入优势裂缝或射孔,临时封堵过度发育裂缝,迫使后续压裂流体进入欠发育裂缝,达到多缝均匀扩展的目的。然而,暂堵后裂缝扩展形态取决于各簇裂缝被封堵的效率[9-10],考虑投球封堵的过程是当前暂堵法压裂数值模拟的难点[11]。目前已有学者进行相关有限元扩展模拟,实现多簇裂缝间的流量分配功能[12-13],但大多数模型无法考虑射孔冲蚀、投球封堵等复杂过程。笔者基于Abaqus平台开发的管单元构建一种水平井多簇压裂的有限元模拟方法,此方法中管单元可与有限元框架单元自由耦合,以实现多缝间的流量动态分配,还可调用管单元损伤系数子程序考虑射孔冲蚀、射孔限流以及投球封堵等功能,进一步实现多场景下水平井多簇裂缝扩展模拟。
1 数值模型
1.1 管单元
流体管单元与流体管连接单元被统称为管单元,它们是一种双孔压节点单元[14]。流体可从管单元的一侧节点流入经另一侧节点流出,经过该单元后产生一定的压力降。基于管单元的特性,此单元可以被方便地开发并应用在水力压裂过程中流体经井筒或射孔的压力损失模拟。
流体管单元通常被用于模拟流体在管流过程中的摩擦阻力损失,压力损失的计算与井筒的长度有关,经过流体管单元的井筒摩擦阻力压降方程[14]满足:
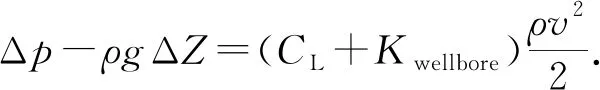
(1)
其中
式中,Δp为流体经过管单元的压力损失,Pa;ΔZ为管单元两节点的高程差,m;v为管单元中的流体速度,m/s;ρ为流体密度,kg/m3;g为重力加速度,m2/s;CL为损失系数;f为管道的摩擦系数,其计算与流体雷诺数有关;L为管道长度,m;Kwellbore为井筒中与方向有关的损失系数;Dh为水力直径,m;Re为流管内流体雷诺数;Ks为管道的粗糙度,mm。
流体管连接单元则用于模拟管流过程中的局部附加压力损失(如阀门开关、管道变径),其计算与井筒长度无关。经过管连接单元的压力损失默认满足伯努利方程,其压力损失方程[14]为
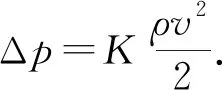
(2)
式中,K为管连接单元的局部损失系数。
另外,多个管连接单元组合形成的管网可以模拟水平井筒中多个射孔簇的流体分配过程(图1)。当管连接单元的孔压节点与有限元框架模型(如二维或三维黏聚区模型)节点组合时,水平井多簇裂缝有限元扩展模型可方便迅速搭建。
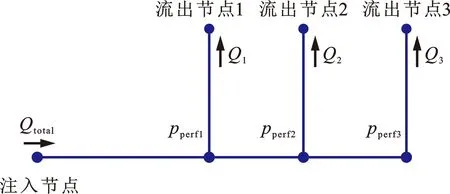
图1 3个管单元组成的管网示意图
管网中流体满足质量守恒方程和能量守恒方程:
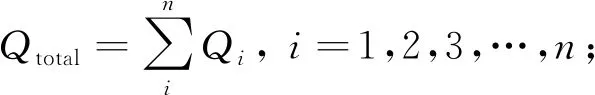
(3)
pwellbore=pout,i+ppf,i+ps,i,i=1,2,3,…,n.
(4)
式中,Qtotal为总注入流量,m3/min;Qi为第i个管单元注入流量,m3/min;pwellbore为注入节点处的流体压力,Pa;pout,i为第i个管单元流出节点压力,Pa;ppf,i为经过第i个管单元的压力降,Pa;ps,i为第i簇裂缝的井筒摩擦压力,Pa。
当满足不同局部压力损失需求时,管连接单元的局部损失系数K可通过ABAQUS用户子程序进行定义,此时可带入射孔摩阻模型或动态封堵模型对此单元的压力损失项进行重新构建。本文中基于管单元给出不同管单元的损失系数定义方程:不考虑冲蚀的射孔摩阻模型;考虑冲蚀的射孔摩阻模型;压裂过程中暂堵球投入的动态封堵模型。
1.1.1 射孔摩阻模型
未考虑冲蚀的射孔摩阻模型通常采用基于伯努利方程的压力降模型[7],表达式为
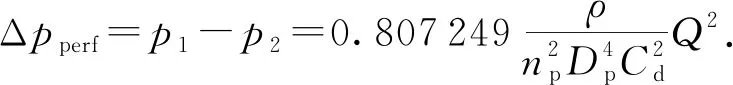
(5)
式中,p1和p2分别为经过射孔簇前、后的压力,Pa;np为单簇射孔簇的射孔个数;Dp为射孔直径,m;Cd为射孔流量系数,0.56~0.90;Q为经过射孔的流量,m3/s。
根据管连接单元压降模型与未考虑冲蚀的射孔摩阻模型的压力降模型等价,则损失项应定义为
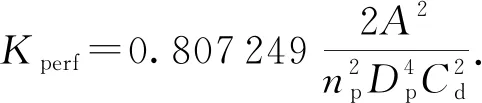
(6)
式中,Kperf为考虑射孔限流条件下的管单元的局部损失系数。
1.1.2 射孔冲蚀模型
由于射孔冲蚀对多簇裂缝流量分配有较大的影响[15],因而在管单元中引入Long等[16]的半解析射孔冲蚀模型,建立可考虑射孔冲蚀的裂缝扩展模型。
除了考虑射孔摩阻方程(5),还应考虑冲蚀后的射孔直径和流量系数的动态变化方程。基于Long等[16]的模型,冲蚀后的射孔直径和射孔流量系数[16]应分别满足:
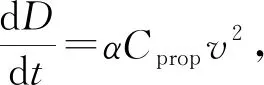
(7)
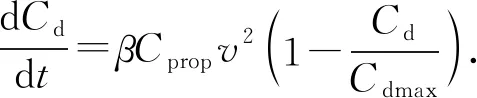
(8)
式中,Cprop为支撑剂质量浓度,kg/m3;α和β分别为与射孔直径、流量系数相关的冲蚀系数,由室内试验测定[16],α=1.07×10-13,β=1.08×10-8;Cdmax为射孔最大流量系数,通常为0.60~0.90。
1.1.3 射孔暂堵模型
暂堵法压裂工艺在压裂过程中投入一定的暂堵球封堵过度改造的裂缝,迫使流体转向未改造的裂缝,从而促使裂缝的均匀扩展。暂堵球的封堵过程采用周彤等[9]提出的等比例分流模型。暂堵时刻各簇裂缝被封堵的射孔数满足:
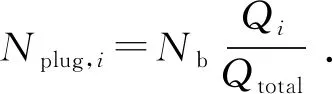
(9)
式中,Nplug,i为第i簇被封堵的射孔个数;Nb为暂堵球的总个数;Qi为第i簇裂缝的暂堵时刻的流量,m3/min。
暂堵后各簇裂缝剩余的射孔数满足:
Nr,i=Np,i-Nplug,i,i=1,2,…,n.
(10)
式中,Np,i为第i簇射孔簇的暂堵前的射孔个数;Nr,i为第i簇暂堵后的射孔个数。
1.2 岩石基质单元
岩石基质单元用于模拟固体形变与流体流动过程,岩石基质单元满足平衡方程[18],表达式为
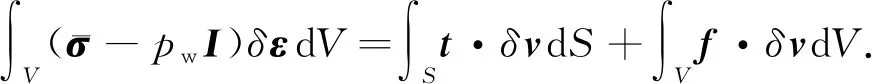
(11)

渗流流体的连续性方程[18]为
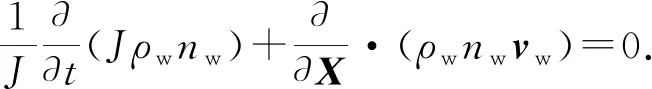
(12)
式中,J为多孔介质体积变化比率;ρw为流体密度,kg/m3;nw为孔隙比;vw为渗流速度,m/s;X为空间向量,m。
流体渗流速度满足达西定律[18],表达式为
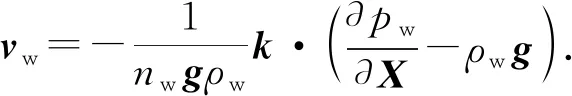
(13)
式中,k为渗透率矩阵,m/s;g为重力加速度向量,m/s2。
1.3 黏聚区单元
黏聚区单元用于模拟裂缝的起裂与扩展,黏聚区模型通常采用双线性T-S法则判定裂缝的萌生与扩展,已被广泛应用于水力压裂模拟[14]。
采用二次正应力准则判定裂缝的起裂,三维黏聚区单元需满足:
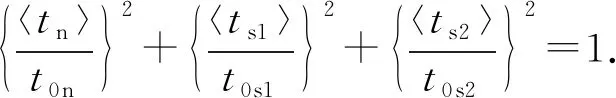
(14)
式中,t0n、t0s1和t0s2分别为无损伤时双线性T-S方程预测的法向、第一切向与第二切向应力,Pa;tn、ts1和ts2分别为真实的法向、第一切向、第二切向应力,Pa。
裂缝起裂后,黏聚区单元产生刚度退化,刚度退化方程满足:
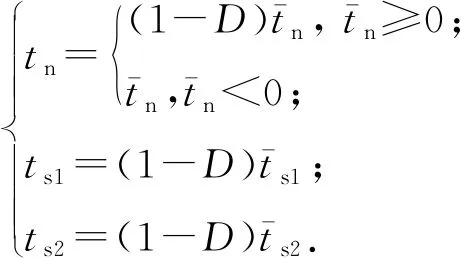
(15)
式中,D为损伤引子。
当黏聚区单元完全损伤时裂缝形成,此时流体在裂缝单元内存在横向流动与法向流动。
横向流动满足方程:
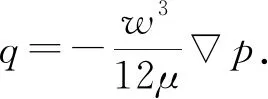
(16)
法向流动满足方程:
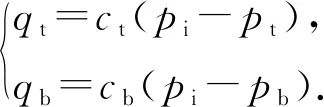
(17)
式中,q为流体沿裂缝流量,m3/s;qt和qb分别为黏聚区单元上壁面、下壁面的滤失流量,m3/s;ct和cb分别为黏聚区单元上壁面、下壁面的滤失系数;pi、pt和pb分别为黏聚区单元中间节点、上壁面节点、下壁面节点的孔隙压力,Pa;w为裂缝缝宽,m。
黏聚力模型中的滤失系数与常规的滤失系数关系为
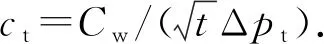
(18)
式中,Cw为滤失系数,m/s0.5;t为自接触后开始滤失的时间,min;Δpt为滤饼前后的应力差,MPa。
裂缝内流体还需满足质量守恒方程:

(19)
2 管单元的验证
为了验证管单元模拟的数值精度,建立水平井三簇裂缝竞争扩展物理模型,并与目前业界认可度较高和应用广泛的全耦合裂缝扩展模型Wu模型[19]进行对比,模型参数与Wu模型参数相同,最大和最小水平应力分别为30.68 和37.58 MPa,注入排量为0.159 m3/s,弹性模量为45 GPa,泊松比为0.2,簇间距为15.24 m,射孔参数为20孔/簇,孔眼直径为0.015 m,滤失系数为1×10-14m/(Pa·s)。通过对比裂缝扩展形态与各簇裂缝进液量完成管单元的数值解验证。基于模型的几何对称性,建立如图2所示的三维有限元半模型,模型尺寸为60 m×160 m×50 m,红色区域代表厚度为30 m的目的层,黄色区域则为厚度为10 m的上下硬隔层,从而限制水力裂缝在缝高上的扩展,这与Wu模型中的等缝高模型类似,储层采用考虑渗流与形变的岩石基质单元C3D8P表征。模型中心区域分布水平井筒,井筒垂深为2 960 m,水平段长度为1 005 m,绿色管线即为井筒示意图,井筒采用管单元FP3D2单元表征,裂缝与井筒之间为射孔簇接触,采用管连接单元FPC3D2单元表征。在模型中心对称分布三簇裂缝,黏聚区单元沿y轴被预置在储层之中,水力裂缝将沿着预置黏聚单元进行扩展,裂缝采用考虑渗流的黏聚区单元COH3D8P表征。为了保证有限元模拟的计算效率与计算精度,近井端采用精细单元尺寸,而远井端采用粗化单元尺寸。本模型共使用35 910个C3D8P单元,2 393个COH3D8P单元,414个FP3D2单元,3个FPC3D2单元。
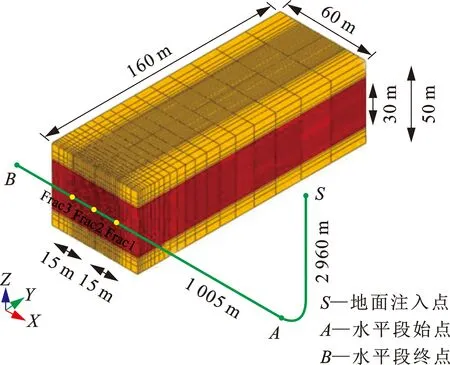
图2 水平井三簇压裂有限元模型
图3为本文中模型计算结果与Wu模型结果[19]对比。图3(a)为裂缝形态的对比,裂缝扩展形态基本一致,但本文模型的裂缝长度稍低于Wu模型[19],中间裂缝这种现象更为明显。这可能是本文模型中采用黏聚区模型T-S法则描述裂缝的起裂与扩展准则,只有满足裂缝起裂准则时裂缝才能扩展。Wu模型则采用亚临界扩展准则进行多裂缝扩展描述,在亚临界扩展模型中裂缝尖端应力强度因子在未达到断裂韧性时,介质内小裂纹仍会发生扩展,陈铭等[20]也进一步指出当亚临界扩展指数较小时,中间簇裂缝扩展形态不同于常规的断裂韧性准则结果,这可能导致Wu模型中间裂缝扩展长度高于本模型。除此之外,在黏聚区裂缝扩展模型中,裂缝仅能沿着预置黏聚区单元方向进行扩展,裂缝无法像边界元方法一样发生偏转,这也可能进一步影响中间裂缝的扩展。图3(b)为各簇裂缝的流量分配结果对比,与裂缝形态结论相似,本文中模型与Wu模型[19]的流量分配结果基本一致,但由于扩展准则差异导致其中间裂缝进液速度低于Wu模型。整体上,采用管单元的有限元模型裂缝形态与流量分配与Wu模型[19]的结果基本一致。
3 管单元在多簇裂缝扩展中的应用
管单元可通过定义不同的局部损失系数完成多场景下的裂缝扩展模拟。在水平井分段多簇压裂作业中,过长的水力裂缝将会造成井间裂缝沟通,从而造成井间压窜,而过短的裂缝则致使储层区域改造不充分。因而多簇裂缝的均衡扩展对储层的有效改造十分重要,现场往往采用投球暂堵法和限流法两种工艺促进多缝的均衡扩展。基于图3模型针对多缝均匀扩展工艺模拟投球暂堵法、限流法压裂、考虑射孔冲蚀的限流法案例,所用模型参数及管单元损失系数方程如表1所示。

表1 管单元在多场景应用案例与所用方程
3.1 投球暂堵案例
如图3(a)所示,验证模型中同时扩展的3簇裂缝缝长差异极大。为了避免这样的结果,现场作业往往投入适量的暂堵球临时封堵部分裂缝的射孔,从而促进多缝的均衡扩展。基于原验证模型,在注入时间为100 s时注入30颗暂堵球(井筒中总射孔数量的一半)进行动态封堵。
图4为原案例与投球暂堵法案例的裂缝形态对比结果。在原案例中,仅有裂缝1与裂缝3得到有效扩展,同时裂缝1的缝长较裂缝3更长,裂缝2几乎不扩展,这是由于裂缝间强烈的应力干扰促使裂缝2无法得到有效扩展[17],同时裂缝1较裂缝3更靠近井筒根部,具有更少的井筒摩阻,从而获得更多的流体进入(图4(a))。在暂堵案例中,3簇裂缝均获得有效扩展,动态封堵后的裂缝2具有更强的裂缝扩展优势,这是由于暂堵球过早或过多地封堵裂缝1与裂缝3,使后续流体大量流入裂缝2,促进裂缝2由劣势裂缝扩展为优势裂缝,因而暂堵球的投入时机与投入数量需要进行优化(图4(b))。通过实时的流量分配曲线(图5)可知,无暂堵案例在压裂初期后流量分配趋于稳定,靠近井筒根部的裂缝1维持在5.15 m3/min,靠近井筒趾部的裂缝3进液排量维持在4.39 m3/min,裂缝2几乎不进液。在暂堵案例中,由于暂堵球的动态封堵,投球时刻(100 s)的裂缝进液排量发生剧烈变化,裂缝1与裂缝3进液排量由5.15、4.39 m3/min分别降低至1.10、1.85 m3/min,裂缝2的进液排量由暂堵前几乎不进液迅速上升至6.69 m3/min。
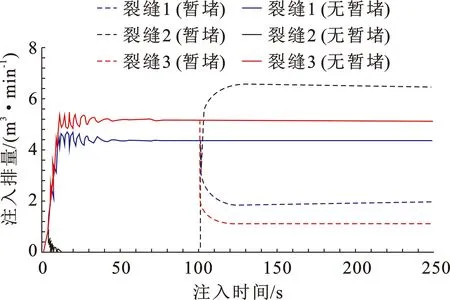
图5 无暂堵案例与暂堵案例的流量分配对比结果
进液排量的剧烈变化是由于投球后各簇裂缝的剩余射孔数差异造成的,由于投球时刻各缝进液排量不同导致被封堵的射孔数量不同,裂缝1、裂缝2、裂缝3由暂堵前均为单簇20孔变为暂堵后单簇射孔数为4、20和6孔。无暂堵案例各缝进液比例分别为46.06%、0.15%和53.78%,而暂堵案例中各缝进液比例分别为29.64%、41.53%和28.83%。这表明投球封堵可以平衡多缝间的均衡进液与裂缝扩展,但更均匀的裂缝则需要对暂堵投球参数进行进一步优化,例如在本案例中推迟投球时机或减少投球数量则更有助于多缝的均衡扩展。
3.2 限流法压裂(射孔冲蚀与未考虑射孔冲蚀)
与暂堵法压裂不同,限流法压裂采用更少的射孔数量增大井内射孔摩阻促进多缝的均衡扩展,已在现场大量应用。然而在携砂阶段,支撑剂对射孔的冲蚀会造成井筒内射孔摩阻下降,从而造成限流失效。模拟单簇射孔数为8个的限流法压裂模型,分别考虑射孔冲蚀与非射孔冲蚀。在冲蚀案例中,注入时间为100 s时,注入720 kg/m3砂浆时进行射孔冲蚀。
图6为未考虑射孔冲蚀与考虑射孔冲蚀的限流法压裂案例。与原模型案例相比(图4(a)),两种场景下的限流法案例3簇裂缝得到有效扩展(图6(a)、(b))。与未考虑射孔冲蚀的限流案例相比,射孔冲蚀导致进液优势的裂缝进一步增大进液,进液优势的裂缝进一步减少进液,增大了裂缝间的扩展差异。
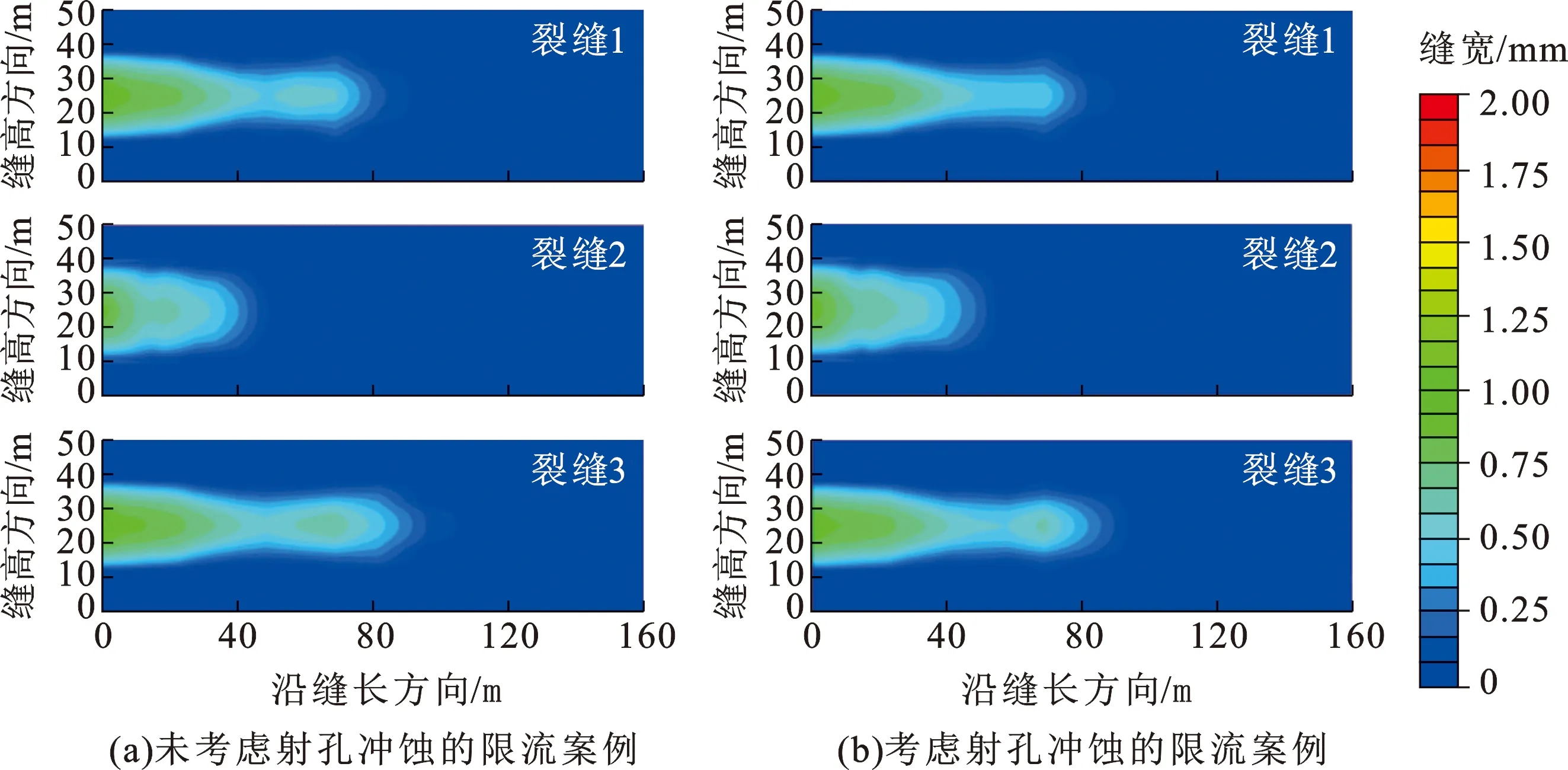
图6 未考虑与考虑射孔冲蚀的裂缝扩展结果
图7为考虑射孔冲蚀时射孔流量系数与射孔直径变化。从图7(a)中可看出,携砂液注入造成3簇裂缝的流量系数迅速增大,增大的幅度由大到小的顺序为裂缝1、裂缝3、裂缝2,截至压裂结束时刻,裂缝1、裂缝2、裂缝3的流量系数分别由初始流量系数0.60增大为0.87、0.82、0.85。图7(b)显示裂缝1、裂缝2、裂缝3的射孔直径由于射孔冲蚀分别增大至15.020、15.012、15.017 mm。为降低模型计算工作量,本案例中的射孔冲蚀时长相对较短,由射孔冲蚀造成的多缝扩展差异变化相对较小,实际现场作业中,携砂液的冲蚀时长一般为30~60 min,由射孔冲蚀造成的缝间扩展差异十分明显。
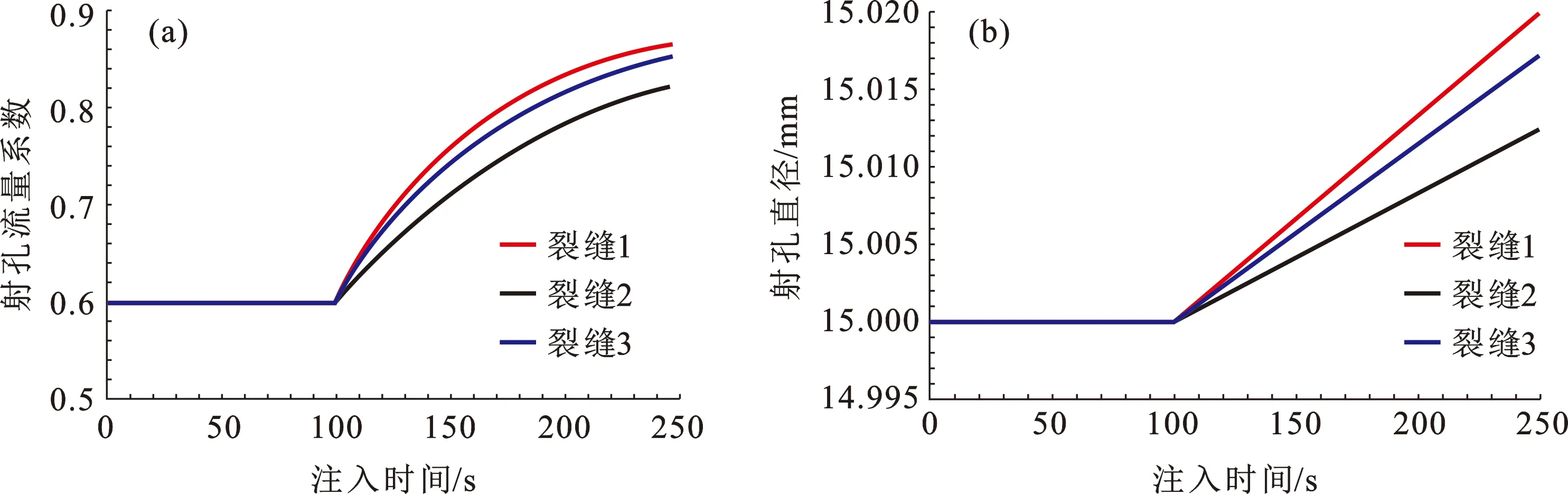
图7 冲蚀案例中的射孔参数结果
图8为考虑冲蚀与未考虑冲蚀案例的裂缝进液曲线。这两种场景下3簇裂缝都得到了有效进液,这表明限流法促进了3簇裂缝的均衡进液。然而,当注入流体为砂浆时(大于100 s),由于射孔冲蚀作用,裂缝进液差异将会进一步增大。例如,裂缝1与裂缝3的进液排量将会逐渐高于未考虑射孔冲蚀案例,而裂缝2的进液排量将会逐渐低于未考虑射孔冲蚀案例。这是由于裂缝1与裂缝3的射孔冲蚀速度要高于裂缝2,造成裂缝1与裂缝3会进一步降低射孔摩阻,增大裂缝的进液量(图8)。进一步统计各簇裂缝的累积进液比例,未考虑冲蚀的裂缝进液比例分别为37.21%、34.75%和28.04%,而考虑冲蚀的裂缝进液比例分别为38.48%、26.40%和35.12%,射孔冲蚀将进一步增大裂缝进液差距。
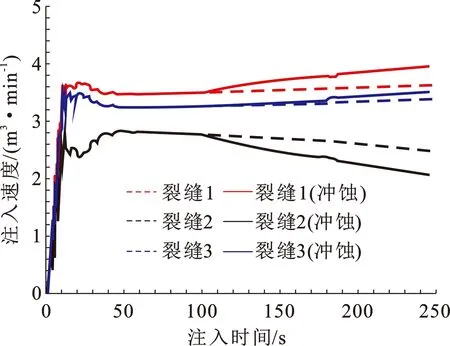
图8 未考虑射孔冲蚀与考虑射孔冲蚀案例的流量分配结果
4 结 论
(1)投球封堵后原本不进液的中间裂缝得到有效进液,原本进液优势的裂缝进液速度得到适当抑制,单段内多簇裂缝可以获得有效的均衡进液,但均衡结果受暂堵时机影响较大。
(2)当携砂液注入后,靠近根部的裂缝更易受到射孔冲蚀,其射孔直径和射孔流量系数都会不断增大,从而进一步降低限流法限流效果,各裂缝的进液差异进一步增大,3簇裂缝中裂缝受射孔冲蚀影响程度由大到小的顺序为根部边缝、趾部边缝、中间裂缝。
