基于改进启发式搜索算法的智能电网电能质量监控

龙蔷

(凯里学院， 建筑工程学院, 贵州， 凯里 556000)

0 引言

智能电网是一种随着计算机、嵌入式、通信等技术发展而兴起的新型系统。其核心思想是将电力传输与分布式网络通过传感器、计算单元以及通信网络相连接，提供了更加灵活、高效的电能管理方式。智能电网的概念一经提出，就备受学者的广泛关注。

智能电网最重要的一个特征就是自愈能力。然而，要实现自愈能力的关键就是要提高电能质量监控(Power quality monitor，PQM)效率。一种解决思路是对电网各节点添加电能监控模块，从而提高电能质量监控能力。考虑到成本以及效率问题，不能简单地对电网无限制添加或减少质量监控模块，因此探索智能电网中监控模块数量以及安装位置的优化问题成为制约智能电网质量监控发展的重要因素，这也是困扰众多学者的难点。

目前，已有众多国内外学者对智能电网电能质量监控进行研究，并取得了一定成果。陈实[1]提出了一种改进的电能质量分析建立电能质量监控系统。该系统能够便捷地分析和检测各类电能质量干扰，如基频偏差、谐波、相间谐波、电压波动以及电能质量事件等。杜俊杰等[2]提出了一种能够对谐波超标进行联动预警与控制的软件逻辑算法。该算法在保障用户设备安全的前提下实现对用户谐波的有效监控，保证了电网母线谐波控制在国标范围之内。上述方法在对电能质量监控时未考虑最优解，而仅仅是找到了一个可行解。C. Ammer等[3]提出了一个基于回归分析的节点检测算法，能够对各节点的相似行为进行评估，从而找出冗余电能质量监控支路。该方法在一定程度上能够减少电能质量监控的数量，但是由于算法是基于大量数据进行分析得到，结果的准确度有待进一步验证。Kaushal J等[4]提出一种利用MATLAB-Simulink软件对单相交流微电网电能质量相关的电参数包括电压、频率、功率因数和总谐波失真等进行评估的决策方法。为了量化电能质量随机变化的模糊性，利用256个基于规则的模糊推理系统对单相微电网模型提出了电能质量监测指标(PQMI)。该方法引入了模糊规则从而进一步精细化电能质量监控指标，然而模糊指标选取合理与否将对结果产生重要影响。选取精度过低造成准确度无法达到实用要求；选取进度过大将对系统造成重大负担。Kamyabi L等[5]提出了一种新的电力系统电能质量监测仪(PQMs)在不同的不可观测深度下的定位方法。在该方法中，考虑到这些器件测量通道数目的限制，将放置问题分为两个层次进行求解。在该方法的第一级，选择不同的连接线组合，而第二级确定在不同的不可观测深度处每个组合的监视器的最佳位置。此外，第二级还识别关键总线，并考虑它们对监控器数量和位置的影响。该方法以不可观测母线上的电压相量估计误差最小以及装置的成本最低为主要目标。因此，该方法将找到安装监控器的最佳位置和这些设备所需的最少通道数，以使所有电能质量参数(即电压和电流相量)可观测。

目前大部分方法的研究重心都在可观测性方面，偶尔会有兼顾定位及考虑安装代价等，因此在实际应用时缺乏一定实用性。为解决上述问题，本文对智能电网中电能质量监控进行了研究，以可观测、定位及安装代价为目标函数，提出了一种改进启发式搜索算法对优化模型进行求解。

1 电能质量监控模型

1.1 电能质量监控可观测模型

电能质量监控的定位问题可抽象为经典数学中组合优化问题。具体描述为

s.t.DX≥b

(1)

其中，C为1×Nb的矩阵，表示在网络节点中安装质量监控设备的代价矩阵，Nb表示系统中节点的数量。X为一个1×Nb的0-1矩阵，元素0表示该节点不需要安装电能质量监控设备，1表示该节点需要安装电能质量监控设备。约束条件中，b为一个1×Nb常数矩阵，表示各电能质量监控设备安装代价要求。D为电能质量监控设备的密度函数，可通过一个m×Nb的观测矩阵A获取，其中m表示观测中的状态变量。观测矩阵的计算公式为

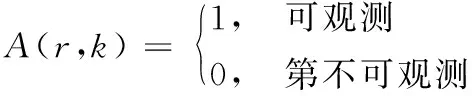
(2)

其中，r为观测变量，k为电能质量监控设备个数。

值得注意的是，当一个智能电网网络节点安装电能质量监控设备后，与其相连接的邻接网络节点也可被观测。接下来引入线路可观测概念。

定义1 当网络拓扑中一条边的两个节点都被安装电能质量监控设备后，那么这条线路被称为可观测。

结合定义1，观测矩阵可被进一步划分为两个部分：观测节点与观测线路，形式化描述为

(3)

其中，Av为NB×NB的观测节点。Ai为NL×NB的观测线路，且NL为线路个数。

因此，观测节点矩阵形式化描述为

(4)

与之类似，观测线路矩阵可描述为

(5)

1.2 电能质量监控定位模型

对于已观测节点，即已安装电能质量监控设备的节点很容易进行定位。然而对于未定位节点，需要进行快速定位，从而保证电能质量监控的效率。

为了优化系统中电能质量监控设备数量以及定位模型，观测节点矩阵Av进一步计算为

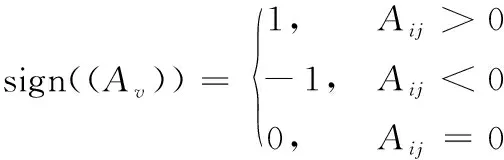
(6)

1.3 电能质量监控安装代价模型

令dij表示智能电网节点i与节点j之间的距离矩阵。同理，距离矩阵也可用来描述电能质量监控设备节点i与节点j之间的电压异常距离。

令dmin表示智能电网中距离矩阵dij最小距离。因此，随着dmin的增大，系统安装代价将快速增加。因此，系统安装代价函数描述为

dmin≤C

(7)

其中，dmin为一常数值，C表示系统代价阈值。

2 解决方法

由于定位模型的基础为可观测，故可得知定位模型条件下的解一定为可观测的。因此，为简化计算，将可观测模型与定位模型进行合并，同时结合安装代价模型，本文提出了一种启发式搜索算法用来求解电能质量监控面临的定位以及安装代价问题。启发式算法将模型求解过程分为两个部分，利用粒子群优化算法(PSO)分别找寻安装代价以及定位问题的最优解。具体过程描述如下。

2.1 代价求解方法

本节将致力于寻求一个最小的安装代价方法。首先，根据前述相关概念，电能质量监控设备的安装代价模型为

costi=(NPQM×PPQM)+(Nch×Pch)+

(Nuch×Puch),i=1,2,…,NPop

(8)

其中，NPQM为安装电能质量监控设备的数量，Nch为电能质量监控设备测量节点电压的通道总数，Nuch为电能质量监控设备未使用的通道总数。同理，PPQM、Pch、Puch为电能监控设备、已使用通道和未使用通道的费用。

(9)

2.2 定位模型求解方法

令模型中总线数量为NBZ，通道数量为ch，则整体计算过程中系统变量尺度为NBZ×ch。根据前述规则可知，系统中评估误差来源都来自未观测到的网络节点。令系统中未观测到节点的数量为NPQM，则评估方程定义为

cost=[cost1,cost2,…,costNPQM]

(10)

同理，PSO算法更新规则方法为

c2r2[g(t)-xi(t)]

xi(t+1)=xi(t)+vi(t+1)

(11)

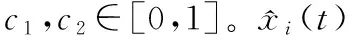
2.3 模型求解过程

结合2.1和2.2节内容，使用带有启发式搜索策略的PSO算法求解电能质量监控模型的具体过程如图1所示。

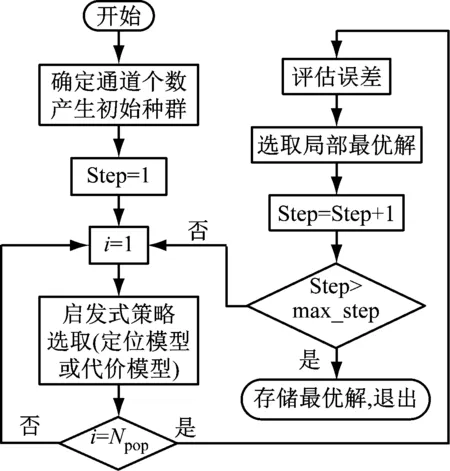
图1 利用PSO算法求解安装代价过程

算法过程可简化步骤如下：

步骤1 初始化；

步骤2 迭代步长step=1，粒子i=1；

步骤3 启发式搜索策略，分别带入定位模型或代价模型；

步骤4 计算评估误差；

步骤5 选取局部最优解，并更新方程；

步骤6 判断是否达到退出条件。

3 仿真与分析

本节设计了一个仿真场景验证本文所提方法的有效性。基础场景参考了文献[6]中IEEE 14总线模型。令仿真场景中节点分支个数为20个，电能质量监控设备为1个，设备安装的位置为7号节点，且与之直接相连的节点有4、8和9号。电力仿真系统所中所设计的一些参数如表1所示。

表1 电力仿真系统参数信息

图2为电力仿真场景中不同通道个数与安装位置代价结果图。

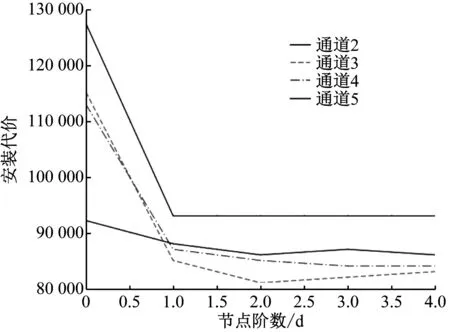
图2 通道个数与安装位置代价结果图

由图2可以看出，随着通道个数增加，安装代价呈现负相关关系。同时，当通道个数为3时，系统整体代价最优。

图3为电力仿真场景中不同通道个数与定位模型代价结果图。同理，当通道个数为3时，系统整体代价最优。

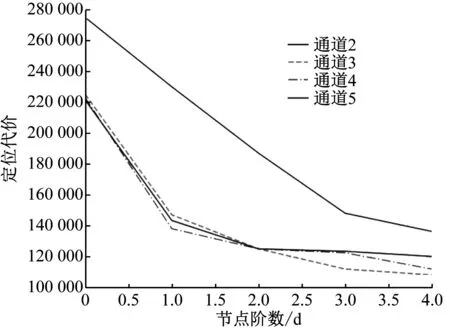
图3 通道个数与定位模型代价结果图

4 总结

为了应对智能电网中电能质量的监控问题，本文提出了一种改进的启发式搜索电能质量监控优化系统，并对系统中PQM定位与代价寻优过程进行了详细阐述。通过仿真分析，结果表明本文提出的方法能够有效维护电力系统的正常运行。该结构为智能电网中电能质量监控的发展提供了一定借鉴和思路。