货运飞船柔性货包装载及建模技术研究
2022-07-26贾东永,雷剑宇*,孙维,白明生,韩彬,于晓洲
贾 东 永, 雷 剑 宇*, 孙 维, 白 明 生, 韩 彬, 于 晓 洲
( 1.中国空间技术研究院 飞行器总体设计部, 北京 100094;2.大连理工大学 工业装备结构分析国家重点实验室, 辽宁 大连 116024 )
0 引 言
在我国空间站建造运营过程中,货运飞船是空间站的一个重要组成部分,每年需通过货运飞船上行运送大量物资[1].当前,国际空间站货物主要依靠进步号[2]、H-II转移飞行船[3-5]、龙飞船[6]和天鹅座飞船[7]运输,货物运输方式与航天器结构形式和整器力学特性紧密相关,有过盈约束、绑扎约束、货柜运输等形式,其中货包类货物多通过舱板和不同数量形式的束缚带纵横交叉紧固限制,在自动转移飞行船、HTV、龙飞船与天鹅座飞船中,货包类货物均采用束缚带绑扎方式[8-9],但是其均在框架式结构上进行束缚安装,不适用于货运飞船蜂窝夹层板结构环境下的安装.
在货运飞船内部,通过特制的柔性货包来装载上行荷载、单机备份件和生活物资等.这种货包装载方式与通常的刚性连接不同,货物先被包裹在货包内部的泡沫缓冲材料里,再通过货包整体固定在蜂窝夹层板结构货架上.特制的柔性货包为上行物资提供了一个缓冲减振的荷载环境,也为货物上行运输提供了更好的适应性和便利性.以天舟一号货运飞船[10]为例,整船装载约100个特制货包,其中货包质量达到5.5 t,约占整船发射质量的40%.货包的质量占比大、阻尼大、刚度低等特点对航天器结构的整体刚度影响较大,在我国航天器结构设计过程中尚未有过相关研究.如何解决通过柔性货包特性仿真建模来开展航天器结构设计成为航天领域一个新的难题.通常的建模思路是将货包描述成刚性单元或均布质量,通过建模仿真计算获得整船的一阶基频,试验后通过参数敏感性分析确定相应的结构修正参数,再通过神经网络模型[11]、模拟退火算法或遗传算法[12]将模型频率设为目标函数,进行全局寻优,获得修正后的模型参数.根据这种方法确定的结构参数与工程实际情况有较大差别,并且每艘货运飞船装载货物均会根据规划和在轨需求调整,各艘货运飞船上行货包的数量和质量也是动态变化的,计算模型必然出现误差.因此,将货包简单视为刚性单元进行仿真计算就不太适应工程实际情况,应将其作为一个货包系统来综合考虑,研究合适的数学模型将货包的物理模型反映到有限元模型中,获得准确的有限元模型,实现货运飞船结构的可验证性设计.
本文针对大量柔性货包对整船基频影响的问题,首先对货包绑扎方式和货包减振形式进行阻尼设计,提出基于BUSH元法的适应货运飞船平台的货包系统建模方法,并在整船振动试验和天舟货运飞船任务中进行验证,以解决动态柔性货包对整船基频影响的问题.
1 货包装载设计
本文主要通过货包内减振材料和货包绑扎方式优化来实现阻尼设计,减小结构在振动过程中的响应,来满足可验证性.为适应宇航货物、仪器设备等在地面运输和上行进入太空过程中经历的复杂力学环境条件,本文研发了图1所示的特种聚氨酯泡沫,采用低毒原料、物理膨胀阻燃、全水发泡技术,克服了现有聚氨酯泡沫气味大、极易燃烧、燃烧产物毒性大等缺点,使泡沫同时具有低气味(1级)、高阻燃、燃烧产物低毒、抗菌防霉(≥99%,0级)及优良的力学性能,满足货运飞船复杂力学环境下货包内部货物的缓冲减振要求.

图1 特种聚氨酯泡沫Fig.1 Special polyurethane foam
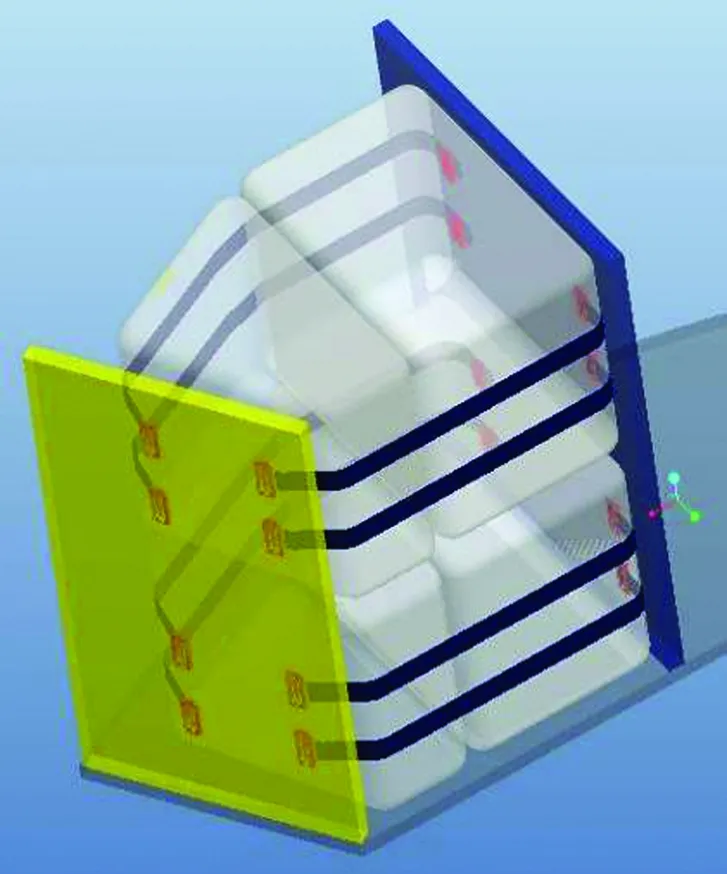
通过分析仿真和对比试验,设计了基于蜂窝夹层板货架结构的货包规格和绑扎方式.货包组合绑扎方式是通过横向和纵向的束缚带以及水平板和立板限制货包X、Y和Z向自由度.典型货包绑扎方案如图2所示.

(a) 通道侧视角
图3为货运飞船内部货包安装的整体情况,货架每个单元格中可组合安装1倍方包、2倍方包、4倍方包、楔形包和梯形包,每个单元格装载上下两层货包,上层货包整体吊在上层仪器板下表面,下层货包整体压在下层仪器板上表面.

图3 货运飞船内部货包安装图Fig.3 Setup diagram of packages in cargo spacecraft
2 货包建模与仿真
2.1 理论模型
Mottershead等[13]把理论模型的不精确主要归结为3个方面.其中之一是模型的参数误差.这种误差主要由对初始模型不精确的简化、近似以及环境变化和生产制造等原因造成材料和几何参数的不确定引起的.对于模型误差,一般先通过参数敏感性分析确定结构的敏感参数,再修正相关模型参数.以货运飞船为例,应用该方法,调整了对刚度较为敏感的蒙皮、连接环节、弹性模量.虽然其频率一致,但实际是一种数学算法上的修正,并不能反映真实情况,对货运飞船模型修正更应着眼于对货包模型不精确简化造成的误差.
在缓冲包装设计中,多采用单自由度线性振动模型[14]或双自由度模型[15]来进行分析计算.参考美军标[16]对货包的简化,本文将试验台-航天器-货包系统简化为一个双自由度的线性系统即图4所示的质量-弹簧-阻尼系统,试验台质量为m1、航天器结构质量为m2、软货包内产品质量为m3,整个货运飞船系统刚度为k1、阻尼为c1.货包与货架的连接刚度为k2、阻尼为c2,其中刚度和阻尼主要由束缚带和泡沫材料提供.整个系统为串联系统,因而忽略货包的刚度k2必然会造成模型修正方法带来的系统误差.
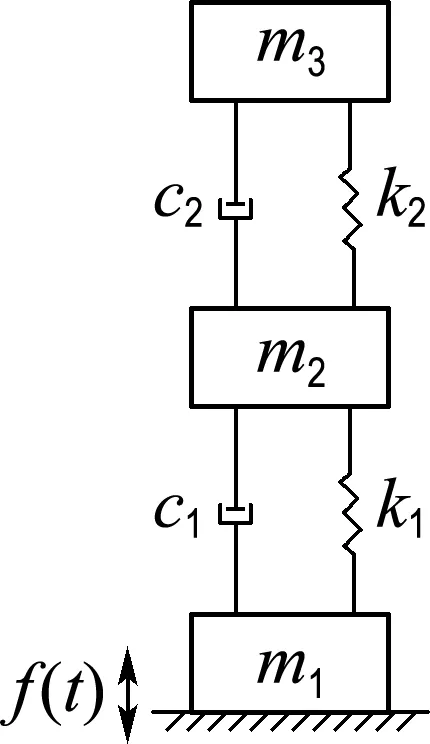
图4 试验台-航天器-货包系统动力学模型Fig.4 Dynamic model of test table-spacecraft-package system
在外力f(t)作用下,系统为受惯性力激励的振动系统,则动力学方程可写作:
(1)
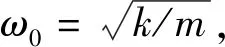
由于m3和m2一起构成货船系统,选取m2、c2、k2和m3作为系统受控对象,在整船系统计算时,k=k1,m=m2+m3,c=c1(根据经验c1可忽略不计).
系统阻尼比ζ计算公式为
(2)
系统共振频率ωm计算公式为
(3)
结构阻尼和刚度都是影响系统基频的重要因素,根据经验货包系统阻尼c2取0.08,依据式(3)计算可得,不考虑阻尼比引起的频率误差仅为0.6%,因此,以整船系统一阶基频为建模修正目标时,可以忽略c2对其的影响,仅需设计局部试验获取k2,再利用k2构造货包有限元模型,进而构造整船有限元模型.
2.2 局部联合振动试验
从整船模型选取局部货架作为子结构,模拟其在整船模型下的力边界和位移边界,设计局部试验并建立对应的仿真有限元模型.将局部试验中基础激励下频响峰值所在频率映射到有限元模型上,由该频率识别货包与结构连接各方向的刚度,将原有根据刚度计算基频的正问题演化为根据基频识别刚度的反问题.
由于货舱内部4个象限的货架结构形式相同且相互独立,局部子结构只选取两层货架结构以及相连接部位的壁板结构.为了保持货架水平方向的刚度,使其更接近整船环境下壁板的刚度,在试验件周围增加了拉杆.底部平板通过螺钉与试验台连接,拉杆与底部平板一起构成了试验的固定工装,局部试验件见图5.传感器安装在货包内的货物上面,用来测试在局部系统下内部货物的频率,传感器位置见图6.局部货架结构和货包联合振动试验如图7所示.
图5 局部试验件Fig.5 Partial test instrument

图6 货包内部结构及传感器位置Fig.6 Internal structure and sensor location inside package

图7 货架与货包局部振动试验图Fig.7 Local vibration test picture of goods shelf and package
2.2.1 货包绑扎方案验证试验 为防止货包产生冲击荷载,货包在蜂窝夹层板结构货架内安装的关键在于对货包进行限位,防止发生大的位移窜动.主要通过绑扎方式设计和货包内减振材料变化降低货包响应的同时提升货包的阻尼效应.
为保证束缚带对软质货包产品3个方向位移进行约束,每个方向上根据限制自由度使用的束缚带根数的不同,分为4种不同的设计方案进行试验对比,如表1所示.

表1 货包束缚安装方案Tab.1 Package belt solutions
表2为4种绑扎方案试验结果对比,如图8所示,图8(a)采用过盈配合加横向束缚带的绑扎方式,操作简单易行;为了增大阻尼效应,减小货包响应,图8(b)将货包采用右端改进型的绑扎方式.通过试验对货包与货架的局部改进绑扎方式效果进行了验证,降低响应效果如表3所示,与原方式相比,新方式X、Y、Z放大倍数分别减少了24%、40%、62%,实现了预期的设计目的.
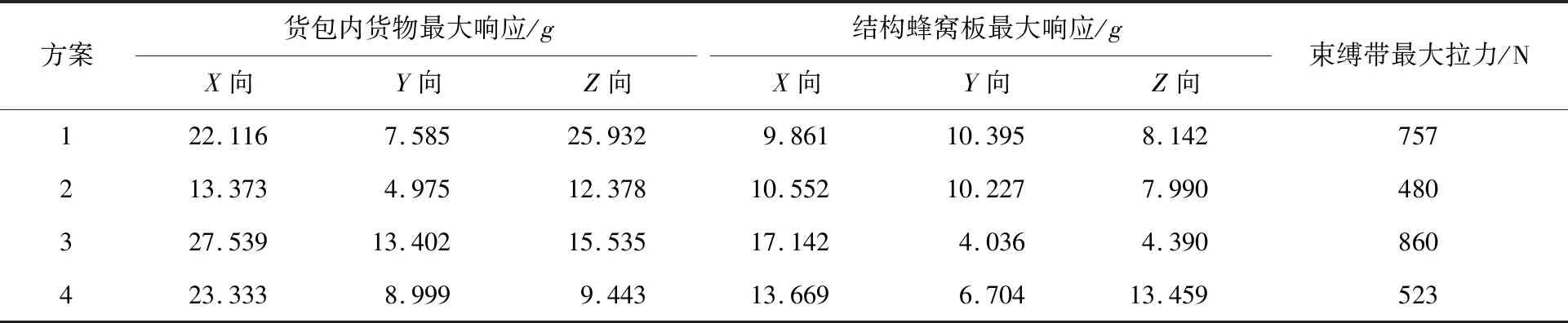
表2 不同货包束缚安装方案试验结果比较Tab.2 Test results comparison of different package belt solutions
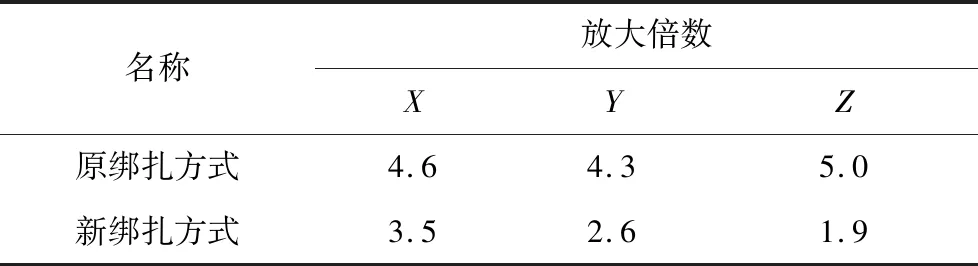
表3 绑扎方式试验结果比较Tab.3 Results comparison of package belt scheme test
(a) 原绑扎方式
2.2.2 货包刚度获取试验 货包内货物的频率与束缚带的松紧程度关系密切,而货包结构经高量级试验后,束缚带的预紧力相对初始状态会有松动.为了模拟货船鉴定级试验时货包束缚带的松紧状态,局部试验鉴定级试验量级选取结构形式类似的天宫一号连接框上的响应,作为局部试验条件.
基于BUSH元的货包建模方式主要有两种.方法一为将货包简化为体单元,每条束缚带与结构的连接点均用一个BUSH元模拟.这种货包建模的好处在于可以针对不同类型货包进行建模,而且可以模拟货包内部刚度的不均衡性.但是这种建模方式如果货包较多,模型规模较大,不适宜在整船模型下使用.方法二为将每格多个货包简化为其质心处的一个质量点,通过一个BUSH元与结构连接,优势在于建模后自由度较少,适于在整船下进行建模.由上文试验可知,每格货包的基频和响应相近,不均衡差异较小,因此选取方法二的方式,图9为基于方法二建立的局部货包有限元模型.在建立图9所示的有限元模型时,按照振动试验状态选取边界条件,取根部固支,按照实际舱体状态依据壳单元模拟进行网格划分,并进行网格无关性检验.
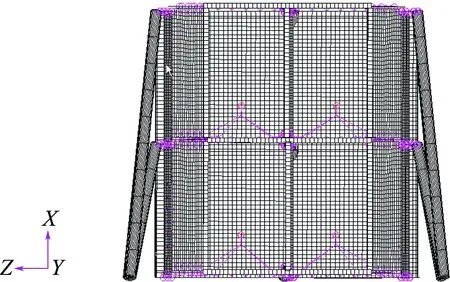
图9 质量点表征货包有限元模型Fig.9 Finite element model using mass point of package
典型货包在基础激励下响应峰值如图10和图11所示,由于重点关注横向频率,因此假设货包的纵向刚度对横向频率不构成影响,取横向即Y向和Z向鉴定级和验收级加速度峰值所在频率点平均值,其中,鉴定级试验相对验收级试验有一定的试验余量,通过取平均值,解决鉴定级试验频率漂移的误差,提高了可靠性;映射到有限元模型中频率分别为7.14 Hz和6.65 Hz,得到BUSH元的Y向和Z向单元刚度如表4所示.在PATRAN中,BUSH元共有6个方向的刚度,在货包局部模型中3个扭转方向和纵向的刚度均设置为无限大.
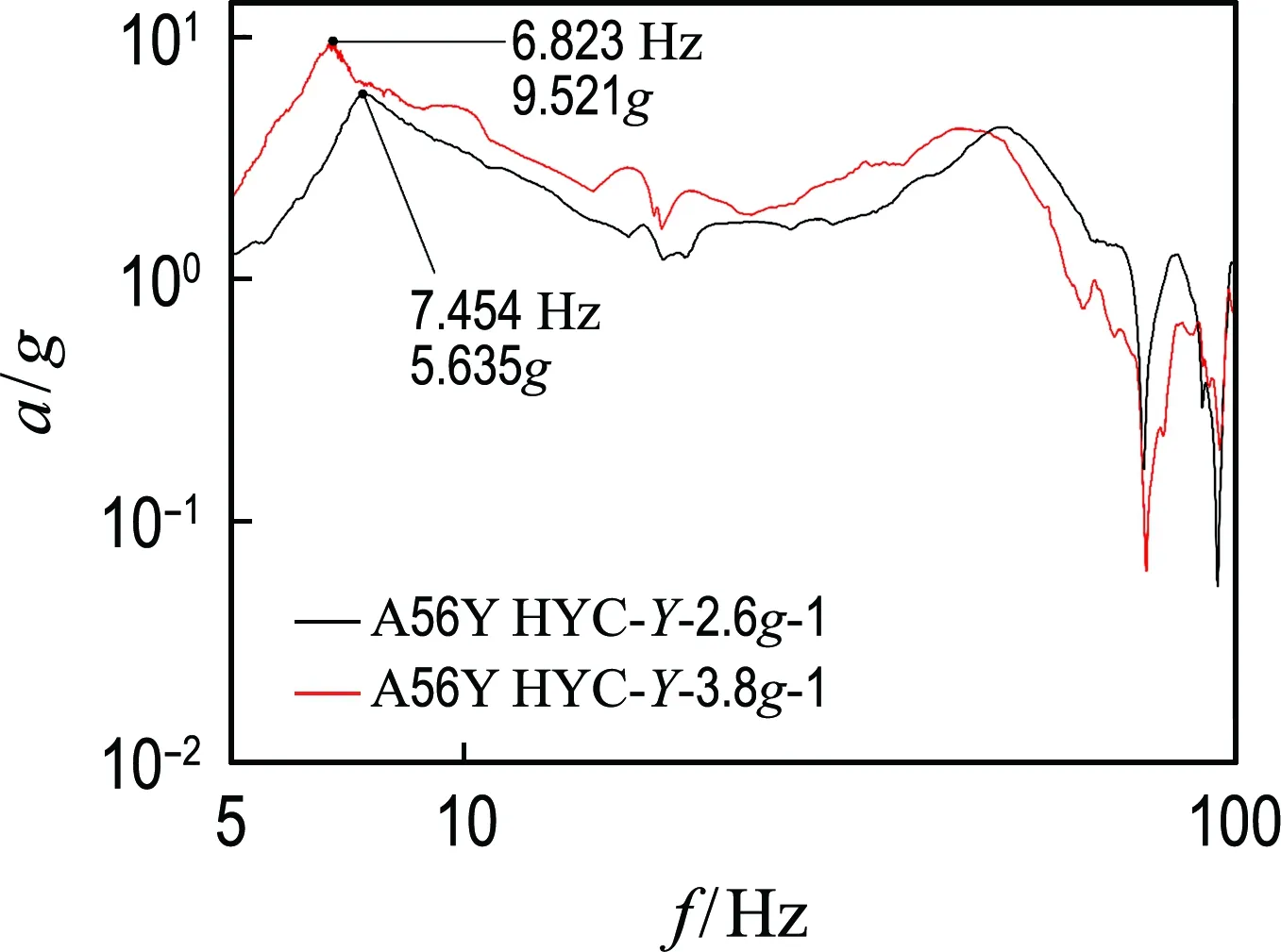
图10 典型测点Y向鉴定级和验收级曲线Fig.10 Authentication and acceptance test curves of typical measure point in Y direction
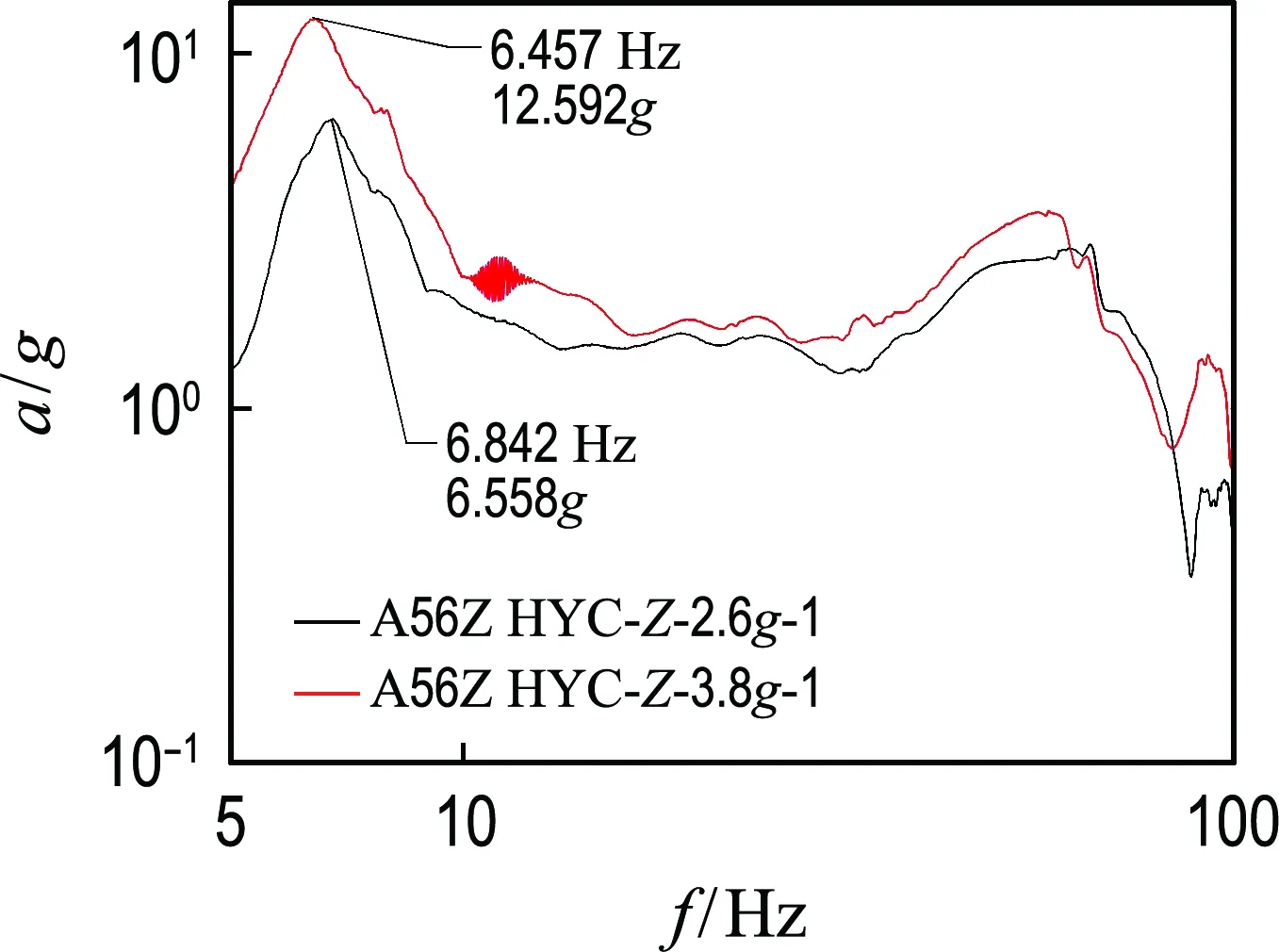
图11 典型测点Z向鉴定级和验收级曲线Fig.11 Authentication and acceptance test curves of typical measure point in Z direction

表4 货包基频及货包连接刚度Tab.4 Fundamental frequency and connection stiffness of packages
2.3 模型建立
为了验证通过质量点和BUSH元模拟货包及货包货架连接刚度的有效性,首先必须排除舱段连接刚度、结构参数等可能误差因素对整船基频的影响.在货包建模前,先根据结构形式类似的天宫一号振动试验获得的基频结果对连接环节和结构参数进行了修正,获得相对准确的结构模型.本文根据货包的质心建立质量点,然后建立BUSH元,通过刚性多点约束MPC(multipoint constraint)单元分别将BUSH元与质量点和货架水平板相连,构成了货包的局部模型,再将由局部试验获取的刚度附在BUSH元上,完成货包模型的建立.货运飞船整船有限元模型共有180 554个节点,191 048个单元.在建立如图12所示的有限元模型时,按照振动试验状态选取边界条件,取根部固支,按照实际舱体状态依据壳单元模拟进行网格划分,并进行网格无关性检验.
图12 BUSH元法货架有限元模型Fig.12 Finite element model of goods shelf using BUSH element method
3 整船试验验证
通过在基础激励下货运飞船整船振动试验响应峰值识别出的基频与仿真结果进行比较来验证本文方法的有效性.货运飞船振动试验就位图见图13,为了保证验证的充分性,选取货包4.4 t和5.5 t两种状态下试验结果进行验证.在识别基频时将根部应变峰值出现的频点作为整船的基频(选取第四次特征级,货包刚度状态与局部试验接近),不同装载下根部应变曲线见图14和图15,不同方法仿真误差比较见表5.根据试验结果,两种状态整船横向一阶基频分别为4.79 Hz和 5.34 Hz,计算值为4.75 Hz和5.30 Hz.两种状态下横向基频误差均由传统方法的10%左右降低至1%,计算结果更接近试验状态,计算精度相比以前有了较大改进.应用该方法,在不同货船上行货包数量或质量调整时,也可以相应调整有限元模型中质量点和BUSH元进行货包的建模.

图13 货运飞船振动试验就位图Fig.13 Vibration test view of cargo spacecraft
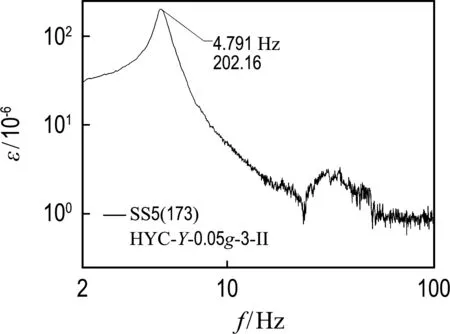
图14 货包5.5 t Y向根部应变曲线Fig.14 Strain curve of 5.5 t package in Y direction base
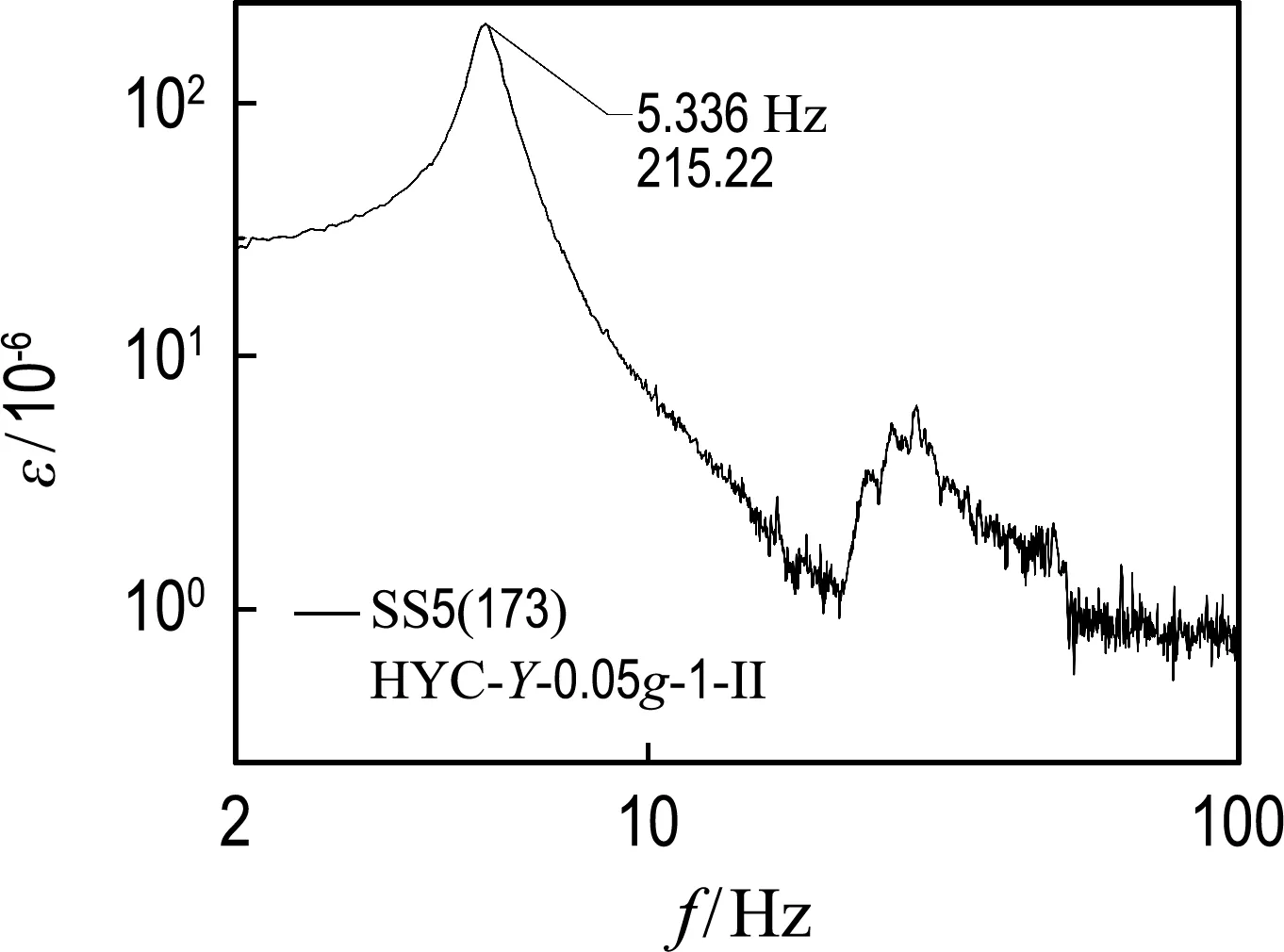
图15 货包4.4 t Y向根部应变曲线Fig.15 Strain curve of 4.4 t package in Y direction base
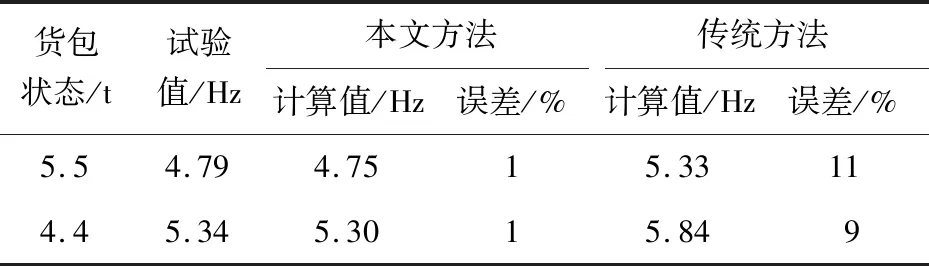
表5 不同方法仿真误差比较Tab.5 Simulation error comparison of different solutions
货包5.5 t状态横向一阶振型图如图16所示.

图16 货包5.5 t状态横向一阶振型图Fig.16 First-order lateral vibration model shapes of 5.5 t package
4 结 论
(1)设计的货包绑扎方案实现了天舟货运飞船5.5 t量级货物的可靠装载固定.
(2)设计了子结构法局部联合振动试验,获取了货包与货架连接刚度关键参数,并使用该参数通过BUSH元和质量点对货包进行了成功模拟.
(3)提出了基于BUSH元的货包建模方法,提高了仿真预测的计算精度,建立的整船有限元模型准确模拟了货运飞船实际状态,并在整船不同货包装载状态下的振动试验中验证了方法和模型的有效性及准确性.
(4)本文提出的方法成功解决了货运飞船面临的大量柔性货包装载影响整船刚度仿真预测的难题,可应用于上行运输大量货包类货物的各种航天器的研制.
