张衡及其数学成就

吴文俊

张衡（78年-139年），字平子，河南南阳人，是中国历史上著名的科学家.张衡青少年时期在京师洛阳游学，写了一些文学作品.24岁时为南阳郡主簿;34岁成为京官郎中;38岁升为太史令，这是当时国家天文历法机构的最高官职;44岁为公车司马令，6年后又复为太史令，最后升为尚书.

在两度担任太史令期间，张衡的科学研究卓有成效，他做过浑仪和浑象等天文仪器，制造过指南车，而他制造的候风地动仪则是我国科学史上的杰作.浑仪和浑象等天文仪器在中国影响深远，可以说后来有关天文的仪器都是在张衡制作的基础上改进和发展起来的.他著有《灵宪》《浑仪图注》《漏水转浑天仪注》《算罔论》等科学著作.其中的《算罔论》被认为是数学著作，但早已失传，其内容无法确知.

张衡研究过《九章算术》则是肯定的.《九章算术》卷四“少广”第24题是：已知球的体积，求其直径.但其求解的步骤（公式）很不精确，竞有大于1/6的误差.张衡是首先注意到这个问题并试图将其解决的人.刘徽在对该题作注时，引了张衡的一段话，并对张衡进行了批评：“张衡算又谓立方为质，立圆为浑.衡言质之与中外之浑：六百七十五尺之面开方除之，不足一，谓外浑积二十六也，内浑二十五之面，谓积五尺也，今徽令质言中浑，浑又言质，则二质相与之率，犹衡二浑相与之率也.衡盖亦先二质之率推以言浑之率也.衡又言质六十四之面，浑二十五之面.质复言浑，谓居质八分之五也.又云：方八之面，圆五之面.圆浑相推，知其复以圆困为方率，浑为圆率也，失之远矣.衡说之自然，欲协其阴阳奇偶之说而不顾疏密矣.虽有文辞，斯乱道破义，病也，”

张衡为了叙述简便，把立方叫做“质”、立圆叫做“浑”.“张衡算”有可能是对张衡《算罔论》的简称.

参考白尚恕的今译，对上面的大段文字作如下解释：

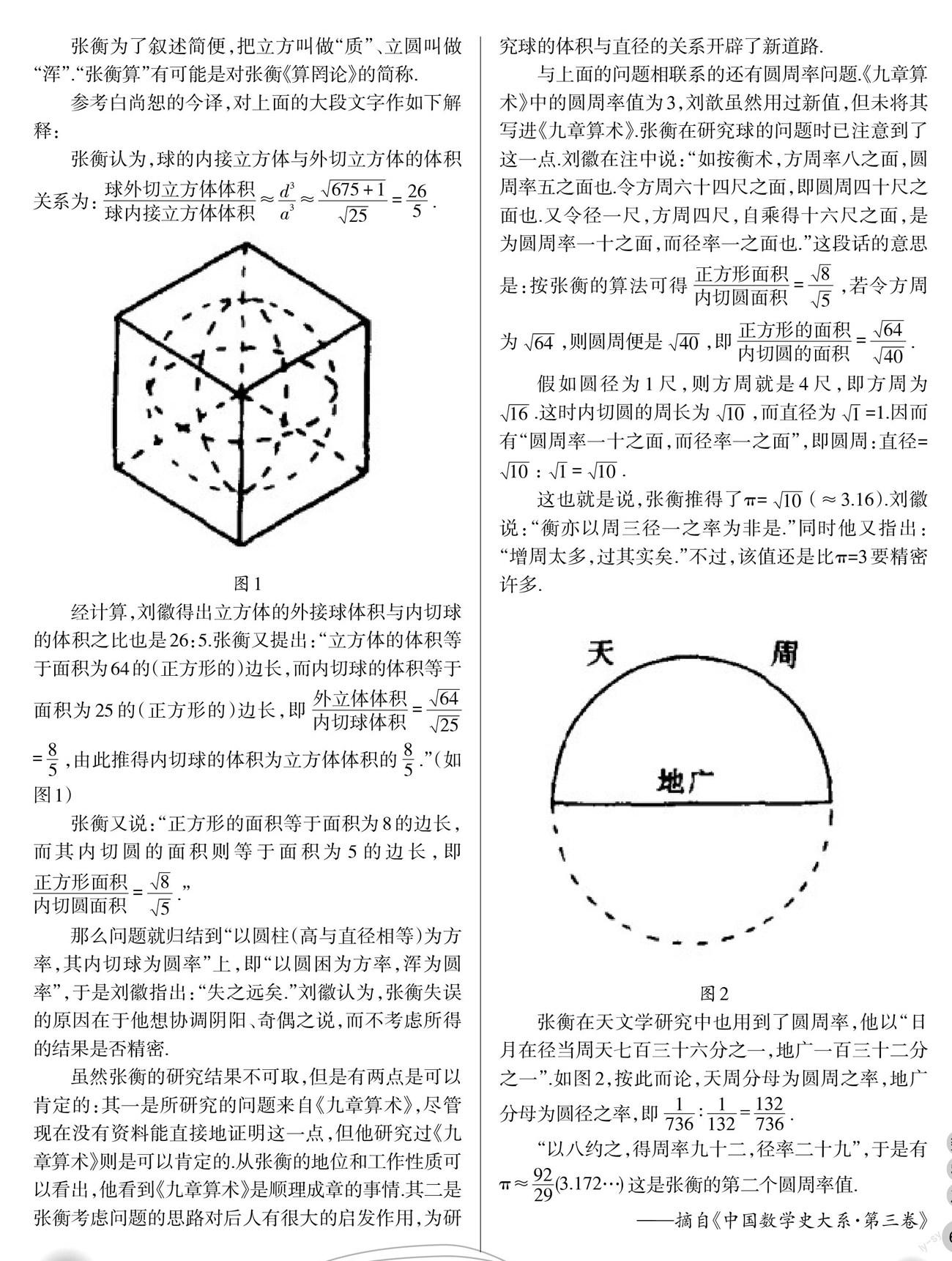
那么问题就归结到“以圆柱（高与直径相等）为方率，其内切球为圆率”上，即“以圆困为方率，浑为圆率”，于是刘徽指出：“失之远矣.”刘徽认为，张衡失误的原因在于他想协调阴阳、奇偶之说，而不考虑所得的结果是否精密，

虽然张衡的研究结果不可取，但是有两点是可以肯定的：其一是所研究的问题来自《九章算术》，尽管现在没有资料能直接地证明这一点，但他研究过《九章算术》则是可以肯定的，从张衡的地位和工作性质可以看出，他看到《九章算术》是顺理成章的事情.其二是张衡考虑问题的思路对后人有很大的启发作用，为研究球的体积与直径的关系开辟了新道路，

与上面的问题相联系的还有圆周率问题.《九章算术》中的圆周率值为3，刘歆虽然用过新值，但未将其写进《九章算术》.张衡在研究球的问题时已注意到了这一点.刘徽在注中说：“如按衡术，方周率八之面，圆周率五之面也.令方周六十四尺之面，即圓周四十尺之面也.又令径一尺，方周四尺，自乘得十六尺之面，是为圆周率一十之面，而径率一之面也.”