临近隧道盾构施工对地表沉降的影响

严 明,匡星晨

(1.太湖县建设安全和人防工程维护管理站，安徽 太湖 246400；2.安徽水利水电职业技术学院 建筑工程学院，安徽 合肥 231603)

0 前 言

近年来，地下工程中关于盾构施工对周边地表影响的分析研究非常多，但是对于临近隧道盾构开挖对地表的影响研究分析还是较少的，本文通过有限差分软件FLAC3D参考实际工况进行了建模和数值模拟，研究在隧道左线和右线分别循环进尺的开挖过程中，对地层产生的扰动，并且这种影响还将随着开挖过程不断地发生变化[1]。

1 工程概况

1.1 工程周边环境

本文以合肥地铁5号线下穿1号线盾构施工段为工程背景，基于盾构施工对周边地表的影响进行模拟分析。1号线为既有的双线隧道，隧道外径为6 m，两线之间的距离设置为11 m，5号线为盾构开挖段，外径也为6 m，两线距离为3 m，1号线和5号线垂直距离为3 m，此时研究5号线盾构施时与1号线的平行段。

1.2 模型参数

根据实际的工程概况，可以将土体分为5层，土层参数按照勘察报告中取值，按照摩尔库伦准则[2-4]进行赋值，土层参数如表1所示。

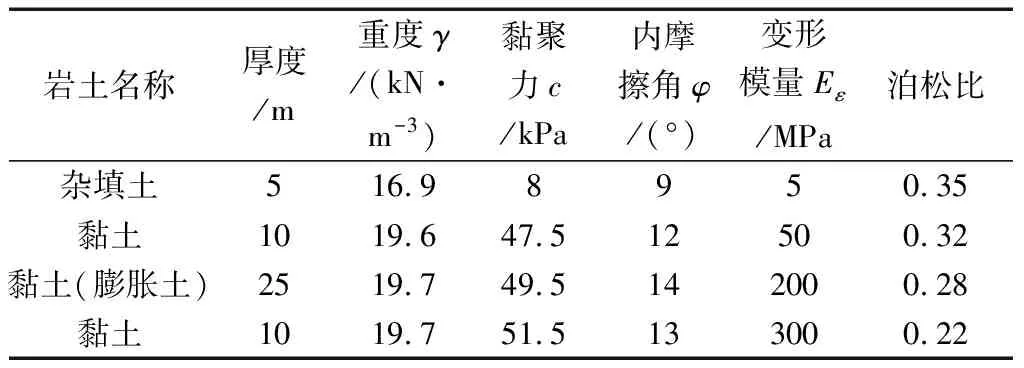
表1 地层物理力学参数

2 数值计算模型

2.1 模型的建立

本文使用有限差分软件FLAC3D进行模拟分析。根据研究内容选取模型整体尺寸为91 m×120 m×50.5 m的长方体，土层根据地质条件分为5层。模型边界条件为：盾构隧道在弹性力学中为平面应变问题，所以对于为盾构隧道掘进的方向，前后面(Y=0，Y=120)约束其Y方向的法向位移；在构建模型时已经考虑了3～5倍洞径范围内应力释放，所以左右面(X=-40.5，X=40.5)不考虑模型的X方向的位移，所以约束其X方向的方向位移；底面为主要持力层，且已经考虑了对竖向方向的影响范围，所以对底面(Z=0)约束其Z方向的位移；上表面为自由地表，不考虑其约束条件，对其不进行约束。模型图如图1所示。

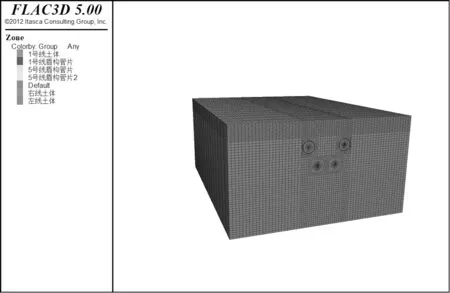
图1 模型整体

2.2 计算基本假定

为了使三维模型计算具有可行性，设定如下[5]：①混凝土接缝、衬砌结构均为线弹性材料；②地表面和土层均为均质水平层状分布；③未考虑水压力和土体加固因素的影响；④只考虑盾构推进为空间位移变化，不考虑时间效应。

2.3 工况设计

本文从左右线分别盾构开挖以及控制开挖掘进距离两个方面来研究盾构开挖对周边地表的影响规律，对其计算结果进行分析。

3 计算结果分析

3.1 1号线双线开挖完成后地表沉降的规律

1号线双线开挖完成后对周围地表沉降的影响如位移云图2所示。

图2 1号线双线开挖完成后位移云图

1)由图2可知，隧道在开挖掘进的过程中会不可避免地对周围的土体造成扰动，这主要是由于开挖后地层损失和土体的应力释放导致的，因而产生了地表的沉降。在5号线未开挖，1号线双线贯通后，由于1号线为双线隧道，地表沉降呈现“W型槽”的趋势，地表最大沉降位置分别在两线的轴线处，而两线的中心线的沉降并不是地表最大沉降位置所在。

2)由隧道的竖向位移云图2可以看出，1号线贯通后，隧道上方土体产生明显的沉降，而隧道底部土体由于地层应力的瞬间释放而产生回弹导致土体向上位移隆起。在远离隧道拱顶的地表沉降最大，越靠近隧道拱顶沉降值越小。

3.2 5号线右线循环进尺开挖后地表沉降的规律

1)由图3可知，在5号线右线开挖过程中，地表沉降发育靠近5号线右线并随着掘进方向同时发育，5号线右线贯穿后，地表沉降呈现“V型槽”的趋势，沉降最大位置偏离五号线中心线靠右，这是由于右线的开挖导致土层的应力释放，土层将会向应力释放的位置发生移动并达到二次平衡状态。

图3 5号线右线开挖60 m时地表沉降与5号线中心距离关系

2)由图3可以看出，在5号线右线开挖过程中，地表沉降的最大值在离5号线中心距离12 m处左右，最大沉降值为3.74 mm。在开挖过程中，当5号线右线掘进到67.5 m处时，沉降基本发育完全。

3.3 5号线左线循环进尺开挖后地表沉降的规律

1)由图4可以看出，5号线左线掘进时，地表沉降继续发育，左线贯通后其最大沉降位置较只开挖右线相比靠近中心线，这是由于在开挖5号线右线后土层中产生较大的塑性破坏，导致在后期开挖5号线左线时，土体的应力释放不再敏感，所以左线开挖完毕后，最大沉降的位置仍然靠近5号线的右线，而不是对称分布。

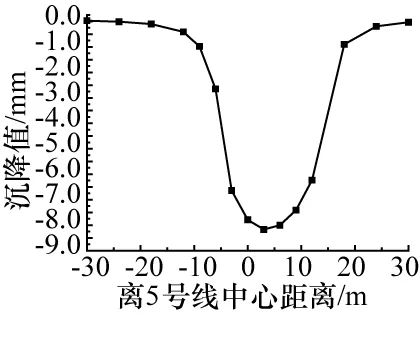
图4 5号线左线开挖60 m时地表沉降与5号线中心距离关系

2)在5号线左线开挖过程中，地表沉降的最大值在离5号线中心距离4 m处左右，最大沉降值为8.19 mm,当左线掘进到60 m处时，沉降基本发育完全。地表沉降发育是一个缓慢的过程，主要是由于应力释放及土层损失所导致，由于在盾构工程中，衬砌施作迅速能有效地抵抗应力的快速释放，所以地表沉降不是马上达到最大值，而是缓慢发育的过程，其随着盾构的推进缓慢发育，一般在10～14倍洞径的范围以后不再发育，此时应力完全释放，由衬砌管片和原有土层共同承担，地层损失在原有范围内也不再发生，此时地表沉降将达到最大值，且不会再发育。

3.4 5号线双线开挖完成后地表沉降的规律

1)由图5可知，最大沉降的位置仍然靠近5号线的右线，并不是对称分布，这是由于施工顺序的先后所决定的，在近距离的施工条件下，其应力释放及塑性区发展范围决定于先开挖的一侧。

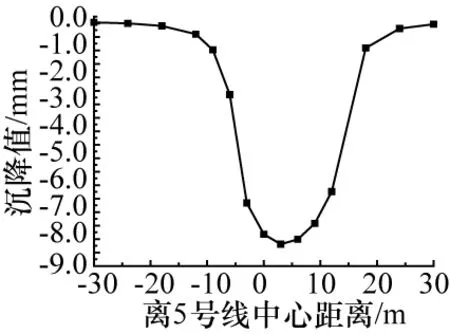
图5 5号线左线开挖120 m时地表沉降与5号线中心距离关系

2)从图5可以看出，5号线左右线贯通后，地表沉降最大位置在距离5号线中心4 m处左右，沿着这个位置基本呈对称趋势向两边延伸，沉降值逐渐减小，在距离5号线中心位置左侧26 m处沉降量基本为零，在左侧26～30 m时，地表向上微微隆起，可以忽略不计。这也说明了模型构建的正确性，两侧约为4倍洞径时，隧道开挖所引起的沉降已经很小，几乎可以忽略不计；在隧道周边约为1～3倍洞径时，是隧道开挖引起的主要影响范围，地表沉降在这个范围里面也发育迅速。隧道开挖实际上是一个土体卸载的过程，上部土体挖出后自重的应力释放，肯定会导致隧道下部土体的膨胀变形，使下部土体回弹。因此，从地表沉降曲线图可以看出，隧道开挖后，由于土体卸荷导致应力释放，速调上部周边地表表现出轻微的隆起状态，而隧道所在位置的上部表现为明显的沉降状态。

3)“PECK”公式在预测双线隧道的地表位移时，考虑两线之间的距离将地表沉降模式分为了两种情况。情况一：当两线之间的距离小于1倍洞径时，其地表沉降发育呈“V型槽”的发育；情况二：当两条隧道间的距离大于1倍小于3倍洞径时其地表沉降曲线呈“W型槽”的发育。从曲线图可以看出，数值模拟出的地表沉降数据完全符合PECK槽的规律，由于5号线左右区间的距离小于1倍洞径，所以地表沉降符合情况一的条件。“V型槽”的开口也随着开挖的推进不断变大，最后稳定在一定的大小。

4 结 论

1)下部线路的开挖对地表沉降的分布也有较大的影响，未开挖下部线路时，地表沉降呈“W型槽”，而随着下部线路的开挖，地表沉降慢慢变为“V型槽”的沉降模式，这是由于下部线路位于既有线中间，开挖导致既有线中间地层的损失和应力释放，引起了地层的沉降；由于叠加的作用，地表的沉降也比未开挖下部线路时的沉降更大，因此，在实际工程中，应该关注地表沉降位置的改变和数值的变化，当周边环境对地表沉降的要求较高时应该采取一定的加固措施，控制地表的沉降；地表的沉降发育与开挖的位置有很大的关系，在开挖一定范围内地表沉降会随着开挖的进行而发育，在距离开挖面1～3倍洞径时是地表沉降的主要发育时间段，而距离开挖面10倍洞径左右的距离后，地表的沉降不会继续发育，会稳定在一定的数值，不再随着开挖的推进而继续发育。

2)预测隧道开挖地表的沉降，应当考虑隧道之间的距离，距离不同出现的地表沉降模式不同，两隧道之间的距离小于1倍洞径时，地表沉降呈现“V型槽”的形式，当两隧道距离超过1倍洞径小于3倍洞径时，其地表沉降模式呈现“W型槽”的形式，两隧道之间的距离超过3倍洞径时，地表的沉降模式更趋近一个“V型槽”的形式，而且在原有线路下方开挖新的线路时，地表的沉降会趋近一个“V型槽”的形式。

[ID:013433]