一类长记忆时间序列趋势项变点的Wilcoxon秩检验

成守尧，陈占寿*，娘毛措，汪肖阳

（1.青海师范大学数学与统计学院，青海 西宁 810008；2.藏语智能信息处理及应用国家重点实验室，青海 西宁 810008）

变点是指随机序列或过程中的某个位置或时刻，变点前、后的观测值或数据服从不同的模型。变点问题早期应用于工业质量控制，后在其他领域中有所发展，如金融、经济、计算机、气象学、流行病学等，引起广泛关注。近年来，各种统计模型中的变点问题得到了较为深入的研究，主要变点类型有均值变点、方差变点、趋势项变点等。本文主要研究时间序列模型趋势项变点的检验问题，其早期研究可参见文献[1]。HUŠKOVÁ等[2]基于极大似然方法构造了检验趋势项变点的统计量，并采用Bootstrap方法近似计算了统计量的临界值。秦瑞兵等[3]基于最小二乘估计残差构造了累积和（cumulative sum，CUSUM）型统计量检验趋势项变点。JIANG等[4]提出了同时检验和估计趋势项变点的SN-NOT方法，将自正则化方法与NOT算法[5]相结合，不仅显著提升了检验效率和估计精度，而且将其成功应用于多个国家新冠病毒感染确诊人数趋势变化分析。TAN等[6]提出了一种基于加权经验特征函数的方法，将其用于估计分布函数变点，并提出了一种参数自适应驱动选择方法，以选取合适的参数。上述均在独立或短记忆模型的假设下研究变点，而有关长记忆时间序列模型变点的研究较少。

分数布朗运动[7]具有长记忆性，其长记忆性由Hurst指数刻画。分数布朗运动可近似拟合具有长记忆性的数据，如水文数据、金融数据等，故其在水文[8]、金融[9-10]等领域应用广泛。WENGER 等[11]提出了固定带宽的CUSUM检验并将其用于长记忆时间序列均值变点。长记忆时间序列模型变点检验方法与最新研究成果可参见文献[12]。基于Wilcoxon 秩检验方法的稳健性，WANG[13]研究了长记忆时间序列模型分布函数变点的检验问题，DEHLING等[14]提出了检验长记忆时间序列均值变点的 Wilcoxon秩方法，BETKEN[15]进一步提出了自正则化的Wilcoxon秩方法检验长记忆时间序列均值变点，由于自正则化方法避免了长期方差估计，在使用时更简便。WENGER等[16]通过改进长期方差的估计提出了一种修正的Wilcoxon秩检验方法。

本文先对观测序列做一阶差分，再基于差分序列构造Wilcoxon秩统计量，以检验分数布朗运动趋势项变点，在原假设下推导检验统计量的极限分布，并用数值模拟方法得到检验统计量的临界值。模拟结果表明，除Hurst指数较大情况外，给出的临界值均能很好地控制经验水平，且经验势随样本量的增大逐渐趋近于1，说明本文提出的检验分数布朗运动趋势项变点的统计量是一致统计量。此外，模拟研究发现，当样本量较大时，本文方法对截距项变点和方差变点是稳健的，即当趋势项不存在变点时，截距项变点和方差变点对检验几乎无影响，经验水平仍接近检验水平；当趋势项存在变点时，截距项变点对经验势的影响很小，而当样本量较小时，经验势随方差变点的增加而降低，但随样本量的增多，经验势仍可趋于1。这意味着用本文方法做趋势项变点检验时，当数据中不存在趋势项变点但存在截距项或方差变点时，不会拒绝不存在趋势项变点的原假设，而当数据中存在趋势项变点时，不论是否存在截距项或方差变点，只要样本量足够大均能检测到趋势项变点。在实例分析中，对1854—1989年北半球经季节调整后的1632个月均气温数据进行了分析，检验结果表明，数据中不存在趋势项变点，这进一步验证了已有研究结论。

1 模型与主要结果

2 数值模拟

表1 极限分布的上α分位数Table 1 Upper α quantile of the limit distribution

然后，研究统计量W n的有限样本性质。在式（1）中，由于假设截距项β0t是不变的，不失一般性，假设β0t=0，β1=1，即在无变点原假设下考虑数据：

的生成过程。在备择假设下，数据生成过程为

取样本容量n=50，100，300，500，趋势项跳跃度Δ=0.05，0.10，考虑变点出现在靠前位置、中间位置、靠后位置3种情况，即取趋势项变点位置参数λ=0.25，0.50，0.75。表2和表3分别为经验水平值和经验势的模拟结果，所有模拟结果均在α=0.05检验水平下经1000次循环得到。

表2 统计量Wn的经验水平值Table 2 The empirical size of statisticWn

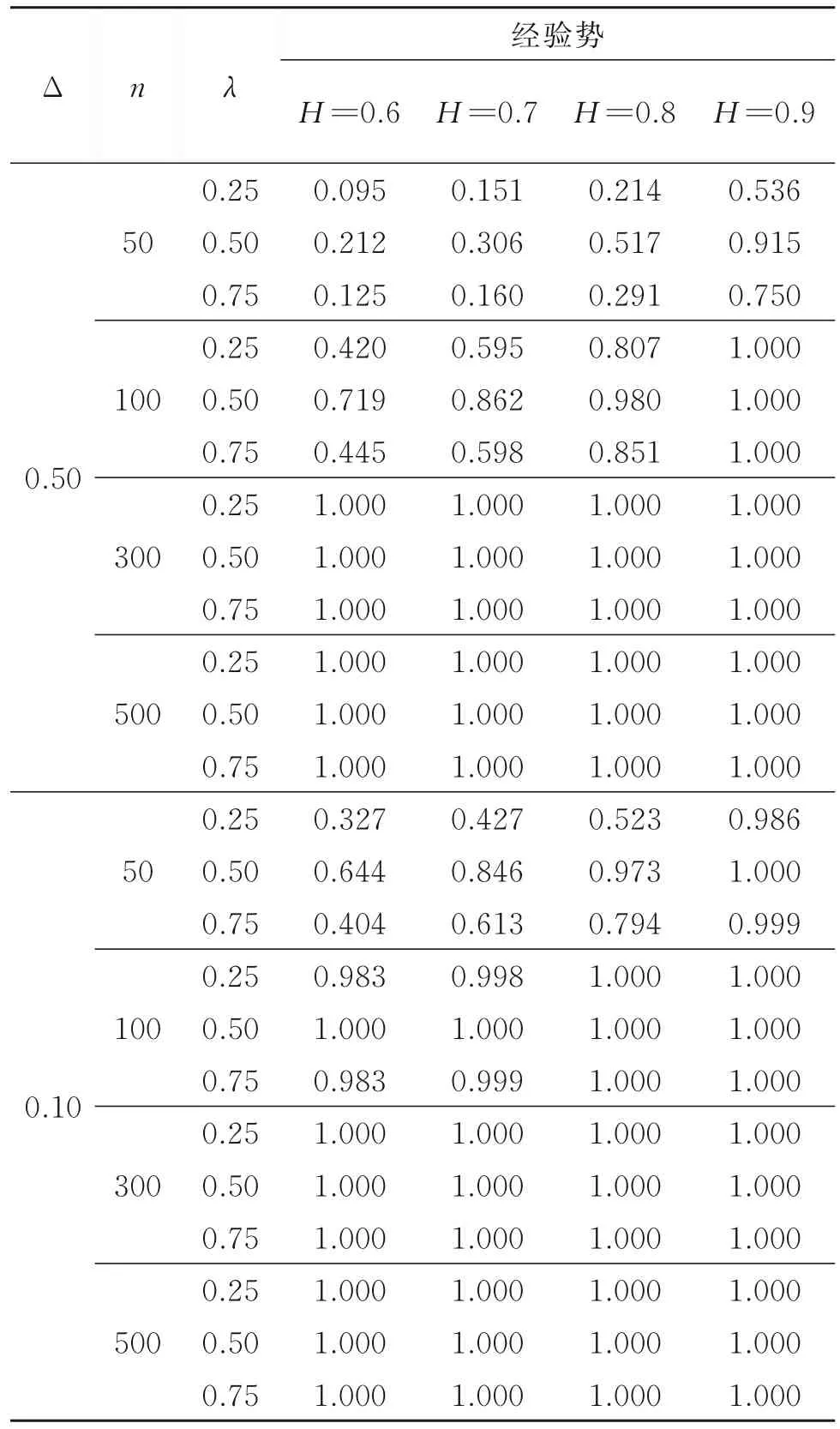
表3 统计量Wn的经验势Table 3 The empirical power of statisticWn

由表2知，当Hurst指数较小时，经验水平值能被较好地控制，且样本量越大，经验水平值越接近于0.05，这是因为随着样本量的增加，检验统计量Wn的经验分布越接近于其极限分布。然而，当H=0.9时，经验水平值出现了较明显的失真，几乎达α的2倍，这是因为此时数据有很强的长记忆性，需要更大的样本量才能较好地控制经验水平。

由表3知，随着样本量的增加，经验势增大，且除了样本量较少的情况外，经验势几乎能达到1。这说明统计量Wn是检验趋势项变点的一致统计量。随着Hurst指数增加，经验势也增大。变点出现在中间位置λ=0.50的经验势较变点出现在靠前位置λ=0.25或靠后位置λ=0.75的经验势大，即变点越靠近中间位置越容易被检验到，这符合大部分后验检验统计量的特点。随着趋势项跳跃度Δ的增加，经验势也随之增大，这符合直观逻辑，因为趋势项跳跃度越大，两组数据的差异越明显，越容易检验出趋势项变点。

上述模拟均假设截距项β0t与误差项的方差是固定不变的，但在实际问题中可能存在截距项变点和误差项方差变点，此时可通过数值模拟分析截距项变点或误差项方差变点对检验统计量的影响。考虑数据：

的生成过程。假设截距项β0t在改变前、后的值分别为 0和β0，取β0=0.5，2.0；误差项的方差变化由σ控制，σ在改变前、后的值分别为1和σ′，取σ′=0.5，2.0。同样，模拟结果均在α=0.05检验水平下经1000次循环得到，进一步假设变点出现在[0.5n]处，讨论以下4种情况。

情况1在无趋势项变点原假设下，β0t在[0.5n]处由 0变为β0；

情况2在无趋势项变点原假设下，σ在[0.5n]处由 1变为σ′；

情况3在有趋势项变点备择假设下，β0t在[0.5n]处由 0变为β0；

情况4在有趋势项变点备择假设下，σ在[0.5n]处由 1变为σ′。

由于情况3和情况4假设存在趋势项变点，因此考虑取趋势项变点位置参数λ=0.50，趋势项跳跃度Δ=0.10。

情况1的模拟结果见表4，由表4知，该结果与表2中的模拟结果很接近，说明截距项β0t变点对经验水平值基本无影响。由于统计量Wn是基于一阶差分数据构造的，而截距项变点对一阶差分数据的影响仅体现在变点上，因此统计量Wn对截距项变点稳健是预期结果。

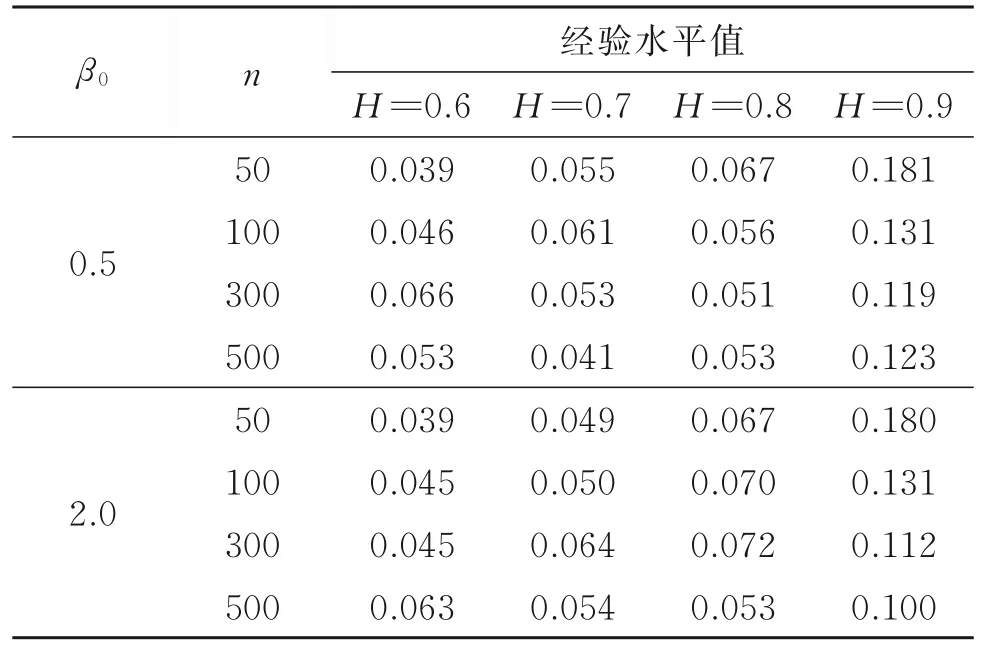
表4 情况1统计量Wn的经验水平值Table 4 The empirical size of statistic Wnin case 1

情况2的模拟结果见表5，由表5知，当样本量较大时，σ的改变对经验水平值的影响较小；当H较大时，σ的改变会使得经验水平值略微增加，但除了H=0.9的情况外，基本上在可接受范围内。因此可以认为，在样本量较大时，本文方法对方差变点也是稳健的。

表5 情况2统计量Wn的经验水平值Table 5 The empirical size of statistic Wnin case 2

由表6知，情况3的模拟结果与表3中Δ=0.10，λ=0.50的模拟结果很接近，表明截距项β0t变点对经验势基本无影响。这亦是因为统计量Wn是基于一阶差分数据所构造的，而截距项变点对一阶差分数据的影响只体现在变点上，所以统计量Wn对截距项变点是稳健的。情况4的模拟结果见表7，由表3中 Δ=0.10，λ=0.50的模拟结果知，当样本量较小时，随着方差的增加，经验势明显减小。这是因为方差增加，使得误差项在数据中的占比增加，导致趋势项的改变对数据的影响降低。在样本量足够大时，经验势仍趋于1，因此可以认为，在较大样本量下，本文方法对方差变点同样是稳健的。

表6 情况3统计量Wn的经验势Table 6 The empirical power of statistic Wnin case 3

表7 情况4统计量Wn的经验势Table 7 The empirical power of statistic Wnin case 4

3 实例分析

将本文方法用于分析1854—1989年北半球经季节调整的月均气温，共1632个观测值，结果如图1所示。

图1 1854—1989年北半球经季节调整的月均气温Fig.1 Seasonally adjusted monthly deviations of the northern hemisphere temperature from 1854 to 1989

首先，对原始序列Yt使用局部whittle估计法，得到其Hurst指数的估计值=0.6939，接近于0.7，此时在α=0.05处的临界值约为0.247。然后，对原始数据Yt做一阶差分得到序列Xt，基于序列Xt计算得到的检验统计量为0.0374，小于临界值0.247，因此认为该组数据中不存在趋势项变点。

此前已有不少研究对该数据集进行了分析，并得到不同结论，如DEO等[23]认为数据存在趋势项变点，WANG[24]则认为没有足够的证据证明序列中存在趋势项变点，SHAO[25]通过检验认为序列存在均值变点。

4 结 论

关于趋势项变点的检验问题，在独立或短记忆模型假设下的研究较多，而在长记忆模型下的研究较少。本文研究了分数布朗运动趋势项变点的检验问题，提出了一种Wilcoxon秩检验方法，基于观测数据的一阶差分序列构造了Wilcoxon秩统计量。在原假设下推导了检验统计量的极限分布。数值模拟结果验证了本文方法在有限样本下的有效性，且在样本量足够大的情况下对截距项变点和方差变点稳健。