建筑工程结构设计值法的应用研究

韩冰

（烟台东源电力设计有限公司，山东 烟台 264000）

现代建筑结构中使用了大量不同物理力学性质的材料进行建造，混凝土、石材、钢材、木材、玻璃等[1]。在结构设计中既要发挥材料本身的工作特性，保证结构的稳定性、强度和变形指标、耐久性指标等要求，也要保证结构材料的选取满足经济合理的要求，以提高工程建设的经济效益[2]。建筑结构的设计方法与力学理论的发展息息相关，以往的按几何学设计或容许应力法设计的理念逐步被实践所摒弃，并逐步发展出了基于概率统计的目标可靠度指标设计方法，在工程建筑结构的设计中体现了材料使用周期内的工作状态，也考虑了结构在建设和运维过程中的不确定性，因此将概率统计的可靠度理论设计方法应用于工程设计更具有科学性[3]。

1 建筑工程可靠度基本计算理论和计算方法

在建筑结构工程建设与使用的全生命周期内，不仅需要承载自身的重力，也会承受各种各样的外荷载，这些外荷载具有恒定的荷载，也有活荷载，比如高大建筑物设计时，需要考虑风荷载，在冬季降雪条件下还应考虑雪荷载。这些荷载的变化不具有确定性，在设计计算阶段的取值实现不了精确计算，因此，为了解决建筑结构的可靠性难题，基于概率统计学理论的设计方法是一个有效的解决途径，让各种不确定的荷载服从某种概率分布形式，衡量不同概率条件下建筑结构是否失效的可能。在建筑结构可靠度理论设计中，设计的主要目的是将建筑结构材料与目标可靠度指标达成一致，以实现最大化地使用结构的材料性能[4]。

在工程结构可靠性的研究中，需要涉及结构状态的的分析方法为极限状态方程，这是描述结构在承受荷载时，整体或者局部超过材料的可承受状态，比如结构的强度超过极限值、结构失去稳定性、发生大变形不适宜进一步承载等，导致结构失去效用，不能够满足设计的预期功能要求。一般而言，涉及到的极限状态有承载能力极限状态和正常使用极限状态。描述结构是否达到极限状态的功能函数如方程（1）所示：

式中，fX（x1，x2,…，xn）为概率密度。

如果结构抗力R 和荷载效应S 均服从正态分布，那么方程（2）可以表达为：

2 基于可靠度指标的建筑工程设计值法

结构可靠度指标与目标可靠度指标之间不可避免地产生偏差，这主要原因是由于在确定设计分项系数时，不同的设计方法存在不同程度的局限性，优化设计方法和设计值法对于确定分项系数的原则有所不一[6]。在优化设计方法中，总体上保持了结构构件计算可靠度与目标可靠度的相互一致，但其前提条件是需要经过荷载和抗力的统计来进行校准，而设计值法则建立荷载组合S、结构抗力R 与目标可靠度值见的相互关系，以更为准确地预估各个荷载分项系数[7]。对于荷载分项系数与结构抗力分项系数的计算如方程（8）、方程（9）所示[8]。

当δR大于0.2 时，可以求得

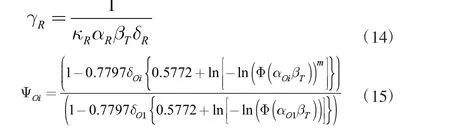
3 设计值法在工程建筑结构计算中的应用

山东省烟台市某房地产建设工程一期位于2018-CH-52 地块，位于城区东北角区域核心商圈范围，附近已有配套公用设施，交通便利。项目总投资95000 万元，项目建设用地约93.6 亩，总建筑面积约241353.70m2，其中地上约174487.20m2，地下约66866.49m2，主要建设14栋24-27 层单元高层住宅建筑、一栋三层幼儿园及四栋低商，居民户数1372 户，容积率2.8，建筑密度19%，绿地率30%，车位配比1:1.1，涵盖高层、复式、第四代住宅、九班制幼儿园、商业等多种业态。在设计取值中，钢筋混凝土等级为C30 混凝土，钢筋材质为HRB335，楼板承受的人群活荷载为4.0kN/m3，楼板的容重取25.0kN/m3，楼板的跨度和板厚分别为3.60m、10cm。

基于建筑工程结构设计法对结构构件的可靠度指标计算，得到荷载效应和结构抗力的分项系数，分别为恒定荷载分项系数γG为1.124，办公楼的活荷载分项系数γQ1为1.295，住宅楼的活荷载分项系数γQ2为1.453，按照风险确定的风荷载γQ3为1.572。建筑钢筋混凝土结构在轴心受压和受弯条件下的可靠度指标计算结果如表1、图1 所示。

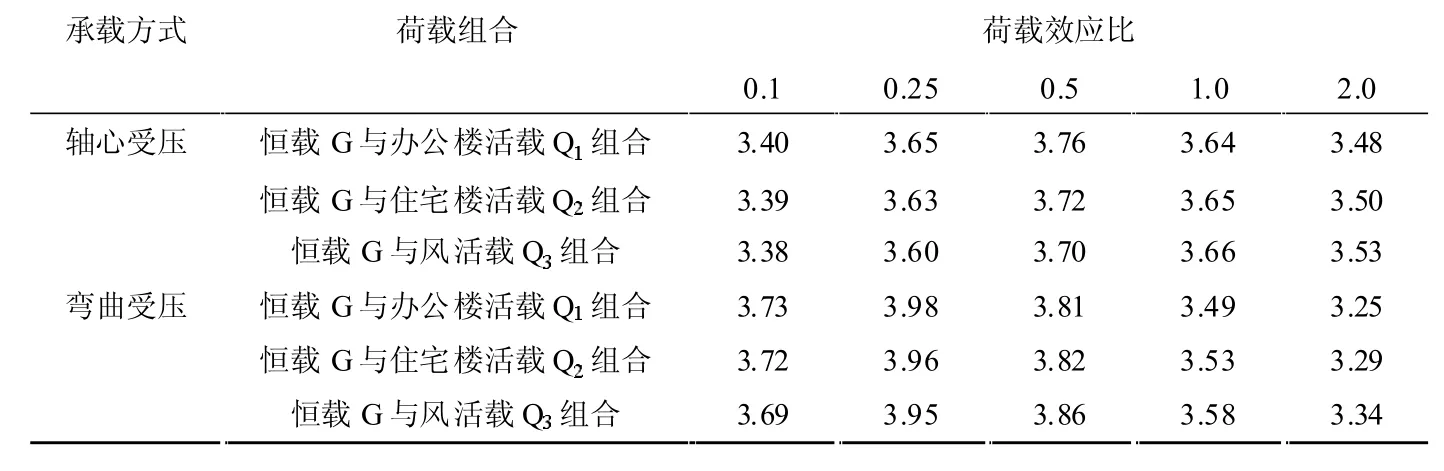
表1 钢筋混凝土结构在轴心受压和受弯条件下的可靠度指标

从图1 中可以看出，随着荷载效应比的增加，钢筋混凝土结构在轴心受压和受弯条件下的可靠度指标曲线均呈现先增加后减小的趋势；不同荷载组合条件下，钢筋混凝土结构在弯曲受压时的可靠度指标峰值均大于钢筋混凝土结构在受轴向应力时的可靠度指标峰值，且可靠度的下降幅度，前者比后者大，因此弯曲受压时的可靠度指标的极小值也比受轴向应力时的可靠度指标极小值小；在同一荷载组合条件下，钢筋混凝土结构的可靠度指标呈现先增加后减小的趋势。

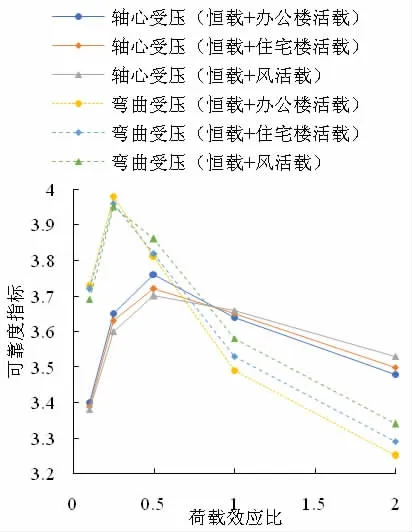
图1 钢混结构在轴心受压和受弯条件下的可靠度指标曲线

图2 为不同荷载组合条件下，钢筋混凝土结构分别受轴心荷载和弯曲荷载的目标可靠度与计算可靠度的计算结果。从图中可以看出，随着计算可靠度的增加，目标可靠度呈现非线性增加，但增加幅度明显减小，呈现逐步收敛的趋势；在相同计算目标可靠度下，轴心受压的目标可靠度大于弯曲受压可靠度；在同受力条件下，相同计算目标可靠度的钢筋混凝土结构，其目标可靠度按照恒载与办公楼活载组合、恒载与住宅楼活载组合、恒载与风荷载组合的顺序依次减小。

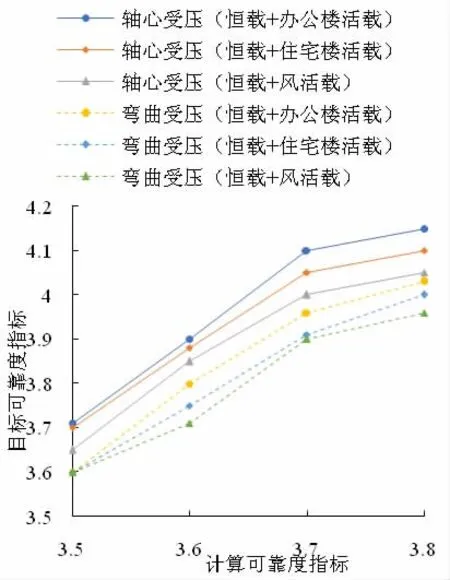
图2 钢混结构的目标可靠度与计算可靠度指标的关系曲线

图3 为基于设计值法对目标可靠度指标的校准，目标可靠度与荷载比的计算结果如图3 所示。从图中可以看出，随着荷载效应比的增加，目标可靠度指标呈现先增加后减小的趋势，目标可靠度指标在荷载效应荷载比为0.4 时达到峰值，峰值大小为4.0。在峰值过后目标可靠度指标的降低没有下限。

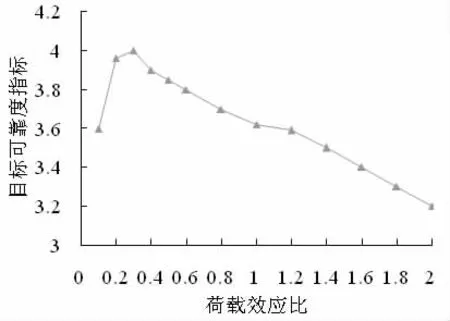
图3 钢混结构的目标可靠度随荷载效应比的变化曲线

4 结论

以山东省烟台市某房地产建设工程一期为研究对象，在介绍建筑工程可靠度基本计算理论和计算方法的基础上，研究钢筋混凝土结构在轴心受压和受弯条件下的可靠度指标变化情况，得到以下几个结论：

4.1 研究表明，随着荷载效应比的增加，钢筋混凝土结构在轴心受压和受弯条件下的可靠度指标曲线均呈现先增加后减小的趋势；在同一荷载组合条件下，钢筋混凝土结构的可靠度指标呈现先增加后减小的趋势。

4.2 随着计算可靠度的增加，目标可靠度呈现非线性增加，呈现逐步收敛的趋势；在相同计算目标可靠度下，轴心受压的目标可靠度大于弯曲受压可靠度。

4.3 随着荷载效应比的增加，目标可靠度指标呈现先增加后减小的趋势，目标可靠度指标在荷载效应荷载比为0.4 时达到峰值，峰值大小为4.0。