相关系数法在岩体结构均质区划分中的运用

乔秀武，张文春

吉林建筑大学 测绘与勘查工程学院,长春 130118

0 引言

在岩体结构的研究中,统计均质区的划分是一项重要内容.其目的就是将相似岩体结构划分到同一区域,岩体在产生和演变的过程中会受到不同的环境作用,导致了岩体的非均匀性,各向异性[1].不同地质单元体在受到荷载时其破坏方式和强度特征不同[2],因此需要将岩体划分为若干个独立区域,将岩体参数相似的地质单元体划归到同一区域.通常在对结构面进行大量野外调查的基础上,运用统计学中随机数学的方法对其进行均质区的划分,一般选择结构面产状为依据进行划分,虽然划分时利用多个参数更加精确,但在具体划分时仍存在诸多困难,因此要根据实际工程需求,通常选择单因素作为划分依据[3-5].

岩体结构均质区的划分在我国起步相对较晚.上世纪80年代,Miller[6]最先提出对均质区的研究,其以迹长为要素并利用列联表结合Schmidt投影网的方法对均质区进行了划分;Kulatilake[7]通过对三峡工程某隧道的研究分析后,运用修正后Miller的方法对其进行了岩体结构均质区的划分;肖尚斌等[8]人通过对某抽水蓄能电站的资料收集整理,然后以产状和密度作为划分参数对其进行了结构均质区的划分;范留明等[9]人以密度作为划分参数对西南某大型水电站侧裂结构面进行了结构均质区的划分;高敬等[10]人通过对甘肃北山岩体高放废物地质处置预选区的资料收集整理,选择最具影响性的要素产状作为划分指标对其进行了均质区的划分,并证明了该方法的可行性.

在对岩体结构进行均质区划分时,多数都以密度、产状为参数对其进行划分,而利用迹长为参数划分的却很少,故本文在前人研究的基础上,运用统计学中的“相关系数法”并以迹长为要素对辽宁某抽水蓄能电站地下厂房主变洞岩体进行均质区的划分.

1 方法介绍

相关系数法是用以反映变量之间相关关系密切程度的统计指标,是按积差法计算的,并以两变量与各自平均值的离差为基础,通过两个离差相乘反映两变量间联系的紧密程度[11],其公式如下：

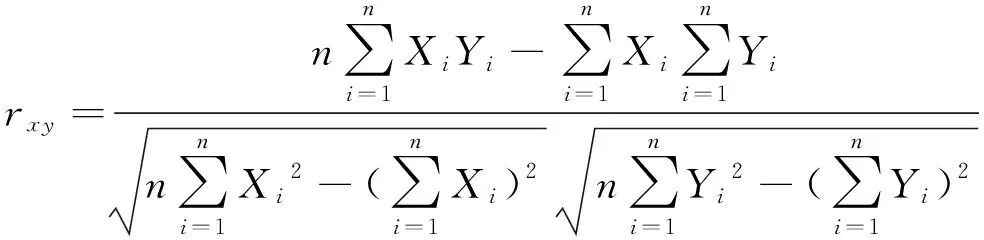
式中,n表示样本数;Xi和Yi表示两个变量间观测值;r表示相关系数,当|r|>0.5时表示两个变量间基本一致,说明两区间的迹长结构分布一致;当0.3<|r|<0.5时表示两个变量间中度相关,说明两区间的迹长结构分布相关不太紧密;当0.1<|r|<0.3时表示两个变量间低度相关,说明两区间的迹长结构分布基本无关;当|r|<0.1时表示两变量间毫无关联,说明两区间的迹长结构分布完全无关,在进行|r|的计算时,其大小基本不受样本数量的影响.

2 工程概括

拟建的抽水蓄能电站位于辽宁省境内,工程等级为一等,其建筑物主要分为永久性主要建筑物、永久性次要建筑物和临时性建筑物.该库区林木茂盛,植被发育良好,少见基岩露头,地表多被残坡积物覆盖,无耕地和房屋,其基岩主要为太古代的变质岩和元古代的侵入岩,现场的地形地貌如图1所示.

图1 地形地貌Fig.1 Topographic map

由于每个工程部位的物理地质性质不同,本文研究的主要区域为平行布置在地下厂房下游侧的主变洞洞室,该区域的岩石类型主要以角闪石花岗岩为主,岩体内裂隙主要以陡倾角为主，穿插有少部分的缓倾角,岩体整体结构较为完整.以往的工程试验表明,该区域岩体的变形模量和抗剪强度均较高,岩体抗变形能力较强.洞室围岩牢固,断层附近两侧岩体受裂隙切割会对周围岩体的局部稳定产生影响,为了更准确地掌握周围岩体的稳定性,需要查清周围岩体的力学特性,故需对其进行结构均质区的划分,本文采用矩形窗口测线法获取6 150 m的局部裂隙迹线图,如图2所示.

图2 二维迹线Fig.2 Two-dimensional trace

3 统计均质区划分

本文以裂隙迹长为参数,利用相关系数法对辽宁某抽水蓄能电站地下厂房主变洞裂隙进行均质区的划分.首先对2个待比样本进行相关密切程度判断,判别原则是利用2个样本间相关系数的大小与0.5做对比,若其大于或者等于0.5,则说明2个对比样本关联紧密,在统计上是一致的,故可以将这2个区间划分为同一个均质区.统计均质区的计算过程如下:

(1) 比较的样本确定. 为了使每个样本内样本数量更加合理,文本选取样本间隔为15 m,建立(0 m～15 m),(15 m～30 m)……(135 m～150 m)共10个待对比样本.

(2) 确定整个区间内所有裂隙迹长的分布. 为了使每个样本内不同长度区间裂隙数合理,将每个区间内裂隙的迹长划分为0 m～1.5 m,1.5 m～3.0 m,3.0 m～4.5 m,4.5 m～6.0 m,>6.0 m共5个区间.

(3) 利用相关系数法的计算公式以及区间(0 m～15 m)和(15 m～30 m)内不同长度区间裂隙的实际频数计算2个区间的相关系数,然后将其与0.5的大小做对比,判别2个对比区间是否属于同一均质区.

(4) 重复步骤(3)依次确定(15 m～30 m)和(30 m～45 m),(30 m～45 m)和(45 m～60 m),……,(120 m～135 m)和(135 m～150 m)能否划分到同一均质区.

通过以上步骤可知,不同待对比样本间裂隙迹长的实际频数及其相关系数见表1.

表1 相关系数法计算结果Table 1 Calculation result of correlation coefficient method

由表1可知,(15 m～30 m)与(30 m～45 m),(75 m～90 m)与(90 m～105 m)的相关系数|r|≥0.5,表明其高度相关,故可将(15 m～30 m)与(30 m～45 m),(75 m～90 m)与(90 m～105 m)划分为同一统计均质区,划分结果如图3所示.

图3 统计均质区划分结果Fig.3 Statistical homogenization division results

4 结论

实际工程中,产状并不是岩体结构划分的唯一标准,划分时一定要选择对实际工程影响最大的要素作为划分依据.本文通过采用相关系数法并以迹长为划分依据对某抽水蓄能电站地下厂房主变洞洞室围岩进行均质区划分,得出如下结论:

(1) 岩体内不同的裂隙迹长可以反映岩体不同的空间分布特征及性质,故本文选择迹长为要素对其进行均质区的划分.

(2) 通过计算两两相邻区间相关系数的大小可知,区间(15 m～30 m)与(30 m～45m),(7 m～90 m)与(90 m～105 m)的相关系数绝对值均大于0.5,故可分别将其划分为同一均质区.

(3) 岩体结构均质区的划分方法有多种,但在利用相关系数法对其进行均质区划分时操作简单易实现,能够合理、便捷地解决类似此场地条件下岩体结构的分区困难问题.