基于批量销售的分布式库存管理研究
2022-07-22王倩楠葛玉辉
王倩楠葛玉辉*孔 飞
(1.上海理工大学 管理学院,上海 200093;2.浙江泰信物产有限公司,浙江 杭州 310002)
0 引言
随着互联网技术进步与消费升级换代,互联网销售和新零售市场的探索和角逐日趋激烈。国家统计局数据显示,2019 年全国实物商品网上零售额8.52 万亿元,比上年增长19.5%,占社会消费品零售总额的比重为20.7%。消费市场对吃、穿、用等日常消费品的品质和购买体验提出了更高的要求,互联网和新零售市场供应链能力成为行业竞争与企业制胜的关键。
传统电商的集中式仓配模式中间环节多、损耗高,是制约供应链总体性能的关键问题。新零售企业不断尝试整合下游需求和上游产地直采,持续优化供应链,在单点库存控制基础上形成的多级库存系统是对供应链资源进行全局优化配置的一种库存管理模式[1],多层级的供应链模型可以灵活应对各种丰富的新零售场景。随着互联网销售和新零售的快速发展,分布式库存系统在实践中的应用越来越广泛,各类企业积极布局中心仓、前置仓、移动支付、云计算等线上、线下领域的协同营销。如京东一直致力于打造多级分仓,不断提高订单响应速度和物流时效,已建立以北京、上海、广州、沈阳、武汉、西安、成都、德州等八大物流中心为基础覆盖全国的销售网络,全国运营超过730 个仓库,物流大件和中小件网络已几乎实现大陆行政区县100%覆盖。凭借其强大的库存管理优势,90%以上的京东自营订单可以在24小时内送达,超160 座城市可实现1 小时极速达。与京东库存管理模式不同,天猫超市原来采用的是集中式库存管理,商品进入菜鸟仓后根据消费者订单从就近仓库发货,在时效性上具有一定的劣势。为抢占市场客流,天猫超市2019 年宣布战略升级,通过大数据锁定消费者高需求高密度区域,在线下联合生态合作伙伴建立近端履约中心提升服务能力,力争低成本、高效率地实现对“最后一公里”商超消费的全面覆盖。对大多数电商来说,通常会在各大区域(如华东地区)设立区域仓(中心仓),而在各城市设立前置仓。图1 展示了电商的库存管理模式。前置仓的设立能够使得顾客在较短时间内取得产品,满足消费者个性化需求,在订单响应速度和配送成本方面都有明显优势。但由于订单的不确定性,电商运营前置仓也面临着货物配置不合理、损耗相对较高等难题。分布式库存管理策略不要求所有仓库的库存均在安全库存以上,只要总库存量保存在系统的安全库存以上,允许个别仓库的库存量降至订货点,从而有效降低整个库存系统的管理成本,并且各仓库之间可在中心仓的协调控制下进行调拨,能降低供应商与生产商之间的协调及配送成本。

图1 电商库存管理模式Figure 1 The inventory management model of E-commerce
对于电商而言,分布式库存管理主要问题之一是如何通过前置仓的需求信息,制定合理、高效的库存策略。具体地说,如何制定中心仓向外部供应商的补货策略;如何制定前置仓向中心仓的补货策略;在中心仓缺货时,如何制定中心仓向前置仓的库存分配策略。同时,批量销售在实际中尤为常见。为了运输的方便或者规模经济的原因,订货量通常有批量的要求,例如酒、水、饮料等通常是以箱为订货单位。因此,研究基于批量销售的分布式库存系统具有重要的现实意义。
多级供应链库存管理研究一直以来都是库存管理研究方向的重要分支。从上世纪50 年代至今,已经引起了众多学者的关注。多级供应链库存管理问题按照供应链的结构可以分为:链式、集成式、分布式以及混合式库存问题。相对而言分布式库存管理系统的研究难度颇大。除了一些相对简单的系统外(例如需求是确定情形下),大部分分布式库存系统的最优策略要么很难完全刻画出来,要么太过于复杂以至于很难在现实中应用。因此,大部分的研究都聚焦在启发式策略的设计。本文首次研究了基于批量销售的分布式库存系统,证明了在平衡假设下系统具有可分性,即原问题可以分解成若干单级库存管理系统。同时,证明可分系统的目标函数具有强Q-跳凸性,从而刻画了在平衡假设下的系统最优策略服从(r,Q)策略。尽管系统可分性大大降低了问题求解的计算量,但是对于大规模问题仍然面临求解困难。因此,本文进一步提出了基于可分性的近视策略,并且证明了该策略的最优条件。
1 相关研究回顾
1.1 分布式库存系统
目前学术界对具有随机需求的分布式库存系统进行了广泛的研究。Simchi-Levi 和Zhao 的综合调查研究比较了多种启发式方法和评估方法的优劣、区别和联系[2]。周期盘点系统的研究可参考Eppen 和Schrage[3]、Graves[4]以及Axsäter[5]等人的文献,连续盘点库存策略可参考Lee 和Moinzadeh[6]、Axsäter[7]的文献。
对于具有一对一补货策略(或等效的订货上限策略)的连续性盘点分布式库存管理研究,Sherbrooke[8]提出了可修复备件多级供应技术(METRIC),用于近似评估全系统成本。这种方法将零售商的提前期近似为运输时间加上由于可能的短缺而导致的仓库平均延迟。此后,Graves[9]开发了改进的启发式方法,Axsäter[10]提出了一种计算全系统成本的精确方法。对于批量订货策略,Duermeyer 和Schwarz[11]对批量订货零售商使用METRIC 类型的方法。Chen 和Zheng[12]检验了梯级库存(r,Q)策略,并提出了一种基于泊松过程需求的对总库存持有量和短缺成本(不包括固定成本)的精确成本评估方法。
一些文献还考察了优于传统(r,Q)策略的优化批量订货策略。Moinzadeh[13]、Axsäter 和Marklund[14]研究了分布式库存系统中的仓库订货问题,在该系统中,多个零售商对同一批量Q 使用(r,Q)策略。Özer[15]检验了具有提前需求信息的分销系统,提出了一种基于从下界问题的解决方案中获得状态依赖的基本库存水平来计算总订单量的启发式策略。然而,上述研究的标准或采用(r,Q)的策略都基于在任何层级均没有明确固定成本的关键假设。
对于分布式库存系统,只有少数文献考虑了固定成本。一部分研究旨在为全系统最优成本提供下界,如Clark 和Scarf[16]、Federgruen 和Zipkin[17]以及Chen 和Zheng[18]。另一部分研究旨在为具有固定成本的分销系统制定启发式策略,特别是收取固定成本的两种不同计费方案:第一种基于每个订单,第二种基于每次运输。前者通常用于生产系统,其中机器安置成本占据大部分的固定成本;而后者在库存分销系统中较为普遍,在该系统中,固定成本通常在物流中产生,如卡车装载运输、拣选和接收。Hu 和Yang[19]考虑了具有固定成本的多级链式库存管理,提出了新的策略改进的多级(r,Q)策略,并证明了其理论效率。Yang 等[20]考虑了具有现货市场的多级集成式库存管理系统,刻画了最优策略。Zhu 等[21]研究了具有固定成本的多级分布式库存系统,证明了改进的多级(r,Q)策略的渐进最优性。
1.2 基于批量订货的库存模型
现有文献已对批量订货模型进行了广泛的研究。Veinott[22]证明了批量订货(r,nQ)策略对于解决单阶段周期性库存盘点问题的最优性。Chen[23]将Veinott 的研究结论扩展至长期平均标准下的多级模型。在此基础上,Chao 和Zhou[24]将Chen 的研究结果拓展到探索可能包含多盘点周期批量订货和固定补货间隔的串行系统的结构特性。以上所有研究均要求系统平稳。Huh 和Janakiraman[25]提出了强Q-跳凸性,将Chen[23]的研究扩展到非平稳环境。强Q-跳凸性的概念也有助于我们分析短视策略的最优条件。Yang等[26]进一步研究了批量订货中的库存定价问题。此外,Yang 等[27]考虑了具有批量订货的多级链式库存系统,证明了若干近视策略的最优性。
从已有研究成果来看,学术界对于分布式的库存管理系统虽进行了深入的探讨,但是还没有文献考虑过基于批量订货的分布式库存系统。本文首次研究了该系统,证明了在平衡假设下系统具有可分性,即原问题可以分解成若干单级库存管理系统。同时,本文证明可分系统的目标函数具有强Q-跳凸性,从而刻画了在平衡假设下的系统最优策略服从(r,Q)策略。尽管系统可分性大大降低了问题求解的计算量,但是对于大规模问题仍然面临求解困难。因此,本文进一步提出了基于可分性的近视策略,并且证明了该策略的最优条件。
2 模型描述
2.1 动态规划模型
多级分布式库存管理系统由一个中心仓库(链级0)和多个前置仓(链级i,i=1,…,N)构成(见图2)。前置仓从中心仓库补充库存,中心仓库可以从外部的供应商订货。假设外部供应商无产能限制。定义c0为中心仓库的单位订购成本,并在不失一般性的情况下将前置仓的单位订购成本设置为零。前置仓的需求是随机的且在各个期间之间独立,但不一定服从同一分布。前置仓之间的需求可能有一定的相关性。每个级的库存补给需要固定的交付时间。假设从外部供应商到中心仓库的订单交货时间为L0,从中心仓库到前置仓i的订单交货时间为Li。前置仓i在每个时期的订单数量都必须是特定批量大小Qi的整数倍,而中心仓在每个时期的订单数量都必须是特定批量大小Q0的整数倍。每级订货不允许分批装运。假设前置仓的批量大小相等,并且中心仓库中的批量大小是零售商批量大小的整数倍,也就是说,存在一个整数m,使得Q0=mQi。需求满足后,剩余库存将结转至下一期,前置仓i的未满足需求(缺货) 也将延期到下期满足,且每个时期内每个缺货订单的实际缺货成本。用和分别表示在中心仓库i和前置仓i处的单位单级库存持有成本。企业的目标是在T时期内将预期的全系统范围总成本降至最低。

图2 分布式库存管理系统Figure 2 Distribution inventory system
每个时期的事件发生顺序如下:每个时期开始时,(1)每级i向其上级i+1 下订单;(2) 每个第i级都将收到从第i+1级在Li期前发出的订单;(3)当期的随机需求实现;(4)各级用手头的库存满足需求并支付相应的库存费用。
参考以往文献,首先介绍以下关键概念。第i级的级库存水平(echelon inventory)是指第i级的现有库存加上其下游所有级或正在转移到其所有下游级的库存减去第1 级的缺货总额。第i级的级库存位置(echelon inventory position)是该级库存的总和加上运输到第i级的库存。第i级的级库存(echelon inventory stock)是第i级的级库存位置与第i级的当前订单数量之和。
该模型采用以下成本核算方案:在时间t,收取在时间t+Li发生的第i级的库存持有/补货成本。该成本会计方案仅在各个时间点之间转移成本,不会影响整个期限范围内的总库存持有量和缺货成本。它的直观解释为:在时间t+Li之前,级i在时间t下的订单不会影响该级i的库存/补货成本。
对于不同时期t=1,2,…,T和不同级i=0,1,2,…,N,定义以下变量:
zi,t=事件(2)中级i的订货数量;
qi,t=,事件(1) 之后阶段i的在途库存,其中是需要在τ时间内达到的库存,τ=1,2,…,Li-1;
定义ΩQ={z|z=mQ,m∈Z+}。由于每个级i的订单大小必须是Qi的非负整数倍,因此表示订单决策zi,t的可行域,即zi,t∈。

公式(1)~(3)刻画出库存动态变化方程。
首先考虑库存决策的约束。可以运到前置仓的总库存值应小于或等于中心仓库的现有库存,即。定义zt=(z1,t,…,zN,t)。因此,周期t中的可行决策集可以表示为:



其中,

在此模型中,对于级i,时段t中的库存订单直到到达该级时才会影响该级的库存水平。因此,可以使用级库存变换的思想来简化建模。将xi,t定义为第i级的库存位置。对于周期t=1,2,…,T,则有

因此,定义以下级变量(echelon variables):

其中yi,t表示在i级的订购后的级库存位置。
在级库存变量下,系统状态的动态方程为:

定义ΩQ(x)={y|y=x+mQ,m∈Z+}。由于每个级i的订单大小必须是Qi的非负整数倍,因此补货后级库存位置决策变量yi,t的可行区域可以用来表示,即yi,t∈。定义xt=(x1,t,x2,t,…,x3,t),及yt=(y1,t,y2,t,…,y3,t)。可行的决策集变为:

用h0表示中心仓库的级库存持有成本率,用hi和bi表示级i处的级库存持有率和缺货成本率。定义。定义与每个级相关的级持有/补货成本如下:

定义Dt=(D1,t,D2,t,…,DN,t),在级库存位置的定义下,原问题的动态规划方程可以写成以下形式:
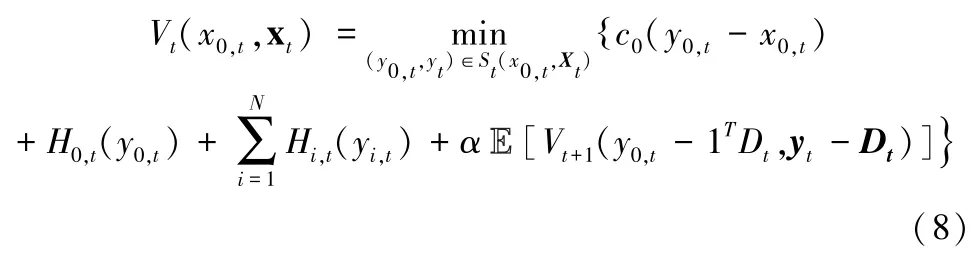
其中相应的终止条件公式为:VT+1(x0,T+1,xT+1)=0。
将(8)称为简化模型的级库存建模公式。针对问题(8),仍然很难获得该问题的最优策略,因为它是一个多维动态规划问题,会面临维数灾难。为了易于处理,需要以下假设。
平衡假设:在每个时期,假设可以将任意两个前置仓持有的库存彼此之间即时地、免费地转运。在平衡假设下,原始问题(4)等价于问题(8)。由于第i级在t期订的货在Li期后到达第i级,也就是说第i级在t期订的货不会影响第i级的库存费用。那么,可以在t期收取第i级的t+Li期的库存费用。如此的计费方式不会影响第i级的库存决策。因此,通过简单的数学变化,可以证明原始问题(4)等价于问题(8)。
2.2 强Q-跳凸性
为了下面的最优策略分析和启发式策略分析,需要下面的函数定义以及相应的性质(参阅Huh 和Janakiraman[25]以及Yang 等[20])。
定义1强Q-跳凸函数。如果对于任何z1∈ℝ,z2∈ℝ,且z1≥z2,函数f(x):ℝ→ℝ,是强Q-跳凸函数,如果满足
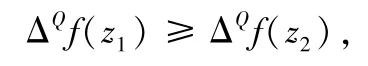
其中ΔQf(x)=f(x+Q)-f(x),以下引理概括了强Q-跳凸函数的一些性质。
引理1强Q-跳凸函数的性质。
(a) 对于某个m∈ℤ+满足Q2=mQ1,如果f(x) 强Q1-跳凸函数,则f(x) 也是强Q2-跳凸函数。
(b) 如果f(x) 是强Q-跳凸函数且α是正标量,则αf(x)也是跳变凸函数。
(c) 任意两个强Q-跳凸函数之和也是强Q 跳变凸函数。
(d) 如果v(x) 是强Q-跳凸函数且W 是非负随机变量,则G(y)=Ew{v(y-W)} 也是强Q-跳凸函数。
(e) 假设fi(x),i=1,….,N是强Q-跳凸函数,则
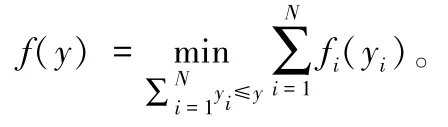
对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,方程f(x):ℤ→ℝ是强Q-跳凸函数,
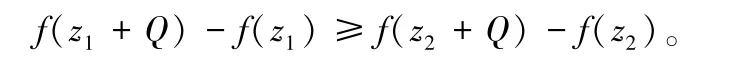
引理1 的证明:
(a) 当f(x) 是强Q1-跳凸函数,满足以下特性:对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,
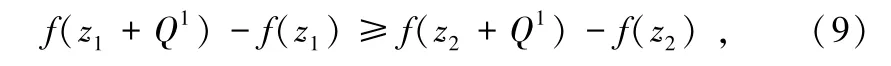
对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,我们有

其中第二个不等式来自(9)。因此,根据强Q-跳凸性的定义,f(x) 是Q2-跳凸函数。
(b) 当f(x) 是强Q-跳凸函数,它满足(9)的特性。可以直接得出对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,

其中第二个不等式来自(9)。因此,αf(x) 也是强Q-跳凸函数。
(c) 假设f(x) 和g(x) 是强Q-跳凸函数,即f(x) 和g(x) 都满足(1)的特性。对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,则有

其中第二个不等式来自(9),因此f(x)+g(x) 也是强Q-跳凸函数。
(d)在不失一般性的前提下,假设W 的分布可以描述为P(w=i)=λi,i=0,1,2,…W,其中W是上限,且=1,则G(y)=。对于任何给定的i,都可以很容易检验出v(y-i) 是强Q-跳凸函数方程。根据(b)和(c),可以认为G(y) 也是强Q-跳凸函数。
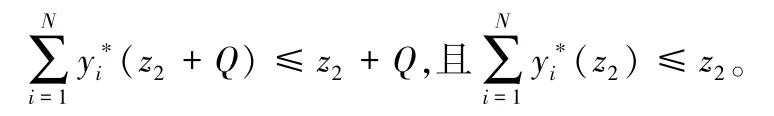
进一步通过两个例子证明以上结果。

梳理以上两个例子得出,对于任意z1∈ℤ,z2∈ℤ,且z1≥z2,

这表明f(x) 也是强Q-跳凸函数,证明完毕。
3 最优策略和启发式策略
本文首先证明在平衡假设下系统具有可分性,即原问题可以分解成若干单级库存管理系统;同时证明可分系统的目标函数具有强Q-跳凸性,从而刻画了在平衡假设下的系统最优策略服从(r,Q)策略;其次,进一步提出了基于可分性的近视策略,并且证明了该策略的最优条件。
3.1 最优策略分析
接下来,本文将在平衡假设下对问题(8)进行后续分析,并简要介绍如何将原始系统分解为N+1 个单级系统的思路。在进一步介绍之前,首先介绍以下级(r,Q) 库存策略:当库存水平降到临界值r以下,则生产/订购足够的产品,以使总库存进入或尽可能接近区间[r,r+Q);否则,无需订货。
对于第i级,i=1,2,…,N,采用以下成本核算方案:在时间t,收取在时间t+Li发生的第i级的库存持有/缺货成本。该成本核算方案仅跨时间点转移成本,因此不会影响整个计划范围内的总库存持有量和缺货成本。它具有直观的解释:在时间t之前,级i在时间t下的订单不会影响级i的库存持有和缺货成本。根据定义,第i级在时期t+Li处的级库存水平为yi,t-,因此,相应的预期持有和缺货成本为Hi,t(yi,t)。
假设中心仓(即级0)的库存充足。在此假设下,级i的问题变为单级库存管理问题,可以建立以下动态规划问题:

定义:

稍后本文将证明目标函数Vi,t(xi,t) 是强Q-跳凸。因此,在时期t,级(ri,t,Qi) 策略对于级i 是最优的。但是,第i级(i=1,2,…,N)可能无法从第0 级获得足够的供货,即第i级的级库存位置受到了第0 级的级库存水平的限制。第0 级无法将第i级的库存位置提高到[ri,t,ri,t+Qi]区间,则以下诱导惩罚成本Γi,t(x) 将计入第0 级:

在时期t,收取在时间t+L0发生的库存持有成本和级0的诱导惩罚成本。然后,级0 的最优成本函数V0,t可以表示为:

可以将周期t中级0 的最大安全库存水平定义为:
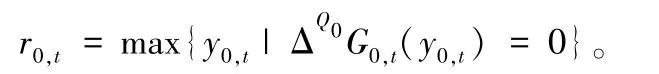
下面的定理表明,目标函数V0,t(x0,t) 具有强Q0-跳凸并且级(r0,t,Q0) 策略是最优的。
定理1对于任意周期t=1,2,…,T 及阶段i=1,2,…,N来说,
(a)目标函数Vi,t(xi,t) 和Γi,t(x) 是强Qi-跳凸;
(b)级(ri,t,Qi) 策略对阶段i来说是最优的。
定理1 证明了一个重要的结果,即可以通过顺序求解N个内嵌函数来获得最优的复购点ri,t,i=1,2,…,N。与原始问题相比,计算复杂度显著地降低了。
定理1 的证明:
首先考虑前置仓的问题。回忆一下前置仓i 面临的动态问题:

通过归纳法证明结果。假设Vi,t+1(xi,t+1)是强Qi-跳凸。从引理1(d)可以得出,αE[Vi,t+1(yi,t-Di,t)]也是强Qi-跳凸。由于Hi,t(yi,t) 具有凸性,引理1(a)表明它是强Qi-跳凸。从引理1(c)可以立即得出,Hi,t(yi,t)+αE[Vi,t+1(yi,t-Di,t)]是强Qi-跳凸。利用引理1(e),可以得出结论Vi,t(xi,t) 也是强Qi-跳凸的,由此完成归纳。
定义:

根据强Qi-跳凸的定义,最优策略遵从(ri,t,Qi) 策略:如果库存水平低于临界值ri,t,则订购足够的产品以使总库存水平进入区间[ri,t,ri,t+Qi) 或尽可能接近;否则,不进行订购。
现在转到级0。级0 面临以下的动态问题:

再次通过归纳法证明结果。假设V0,t+1(x0,t+1)是强Q0-跳凸。从引理1(d)得出,也是强Q0-跳凸。同样地,可以证明G0,t(y0,t) 是强Q0-跳凸。利用引理1,可以得出结论,V0,t(x0,t) 是强Q0-跳凸,由此完成归纳。
可以将周期t中阶段0 的最大再次订购点定义为
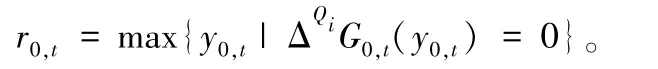
根据强Q0-跳凸的定义,最优策略遵循(r0,t,Q0) 策略:如果安全库存水平为r0,t,则订购足够的产品以使总库存水平进入区间[r0,t,r0,t+Q0) 或尽可能接近它;否则,不进行订购。
3.2 近视策略分析
尽管平衡假设下的最优策略可以将原始问题分解为解决一系列N+1 个一维动态规划问题而大大简化了计算,但是此过程并不透明并仍需解决N+1 个动态问题。接下来,本文介绍计算量较少的近视策略,并描述了近视策略的最优条件。
再次假设中心仓(即级0)的库存充足。级i=1,2,…,N 面临以下短视问题:
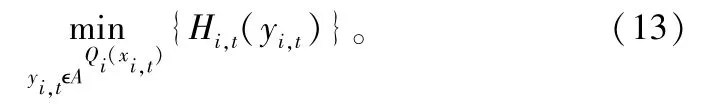
由于Hi,t(yi,t) 是一个凸函数,它也是强Qi-跳凸的。
定义:

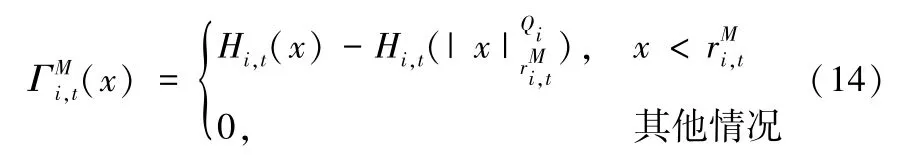
在周期t,对级0 收取库存持有成本,并且在时间 t+L0时实现对级0 收取的罚价。级0 需要解决以下短视问题:

同样地,可以证明KM(y) 和都是强Q0-跳凸。定义:
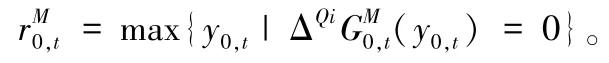
定理2如果需求关于期数是随机递增的,则近视策略是最佳的。
定理2 的证明:
首先证明当需求平稳的,对于阶段i=1,2,…,N,近视策略是最优的。类似的证明可以应用于级0。首先,回顾前置仓i面临的以下动态问题:

定义:

根据包络定理,则有:
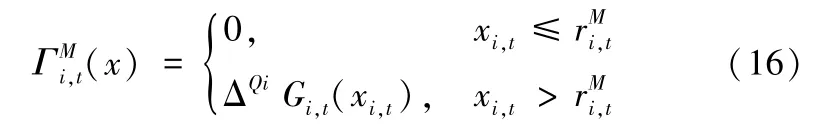
此外,对于任意xi,t>ri,t,ΔQi Gi,t(xi,t)>0。
通过归纳法证明ri,t=,对于t=T,则有:
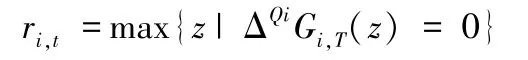
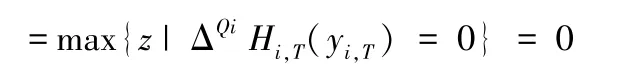
假设结果在周期t+1 成立,即ri,t+1=。接下来,证明它在周期t内也成立,即ri,t=。注意由于ri,t-Di,t≤ri,t+1=,因而根据(16),对于任意已实现的Di,t来说,=0。因此:

第二个等式来自ri,t的定义。
对于任意x>ri,t根据ri,t的定义,ΔQi Hi,t(x)>0。因此,可以得到:

其中不等式来自(16)。
注意到(17)和 (18)表示ri,t=max{z|ΔQiGi,T(z)=0}=,因此归纳完成,级(ri,t,Qi) 策略在t期是最佳的。
目前为止,已经证明该条件是充分条件,但仍然有必要表明这也是必要条件,下面将通过反证法加以证明。
假设对于某个t,P(ri,t-Di,t >ri,t+1)>0,并且对于任意t=1,2,…,T,ri,τ=。否则,结果显然成立。此后可有P(ri,t-Di,t>)>0,并且根据(16),得到

因此,以下结果成立:

这与rt=的事实相矛盾。因此,该条件也是必要条件。
当需求关于期数是随机递增的,可以证明ri,t关于时间t是单调递增的,那么可以通过以上类似的证明过程,证明近视策略也是最优的,证明完毕。
4 总结
本文研究了基于批量销售的分布式库存管理系统,通过建立相应的动态规划模型,证明了在平衡假设下系统具有可分性,即原问题可以分解成若干单级库存管理系统。同时,本文证明可分系统的目标函数具有强Q-跳凸性,从而刻画了在平衡假设下的系统最优策略服从(r,Q)策略。尽管系统可分性大大降低了问题求解的计算量,但是对于大规模问题仍然面临求解困难。因此,进一步提出了基于可分性的近视策略,并且证明了该策略的最优条件。
本文的理论结果是基于平衡假设的前提。实际中,前置仓之间的调货并不一定是即时、免费的。因此,如果研究更常规的分布式管理系统非常具有实际和理论意义。其次,考虑多渠道的需求问题,即前置仓可以同时满足线上线下的需求,同时中心仓也可以同时满足线上线下的需求。但消费者对于两者的体验有所不同。受新冠疫情影响,电商新用户数量大幅增加,线上消费人群和消费习惯发生变化,促使销售额出现井喷。长远来看,消费市场供应链持续优化,传统渠道持续向现代化渠道转移,高效触达差异化消费者,形成规模优势,精细化降低成本,各类业态调整仍有较大空间。如何根据不同、类似的顾客需求以及及时的库存水平来制定合理的库存策略也是未来研究的一个方向。
