树枝形专用线非直达车流取送的三阶段综合协调优化
2022-07-22李明向
李 冰 李明向 轩 华
(郑州大学 管理工程学院,河南 郑州 450001)
0 引言
铁路枢纽是庞大而复杂的系统,在列流、车流和货流相互交汇的铁路端点、工业中心和大都市区往往会形成铁路枢纽。枢纽内集中配置有数量众多的专用车站(编组站和装卸站)和铁路线路,通过对这些设备的合理运用,来完成列流、车流和货流集散与中转任务。
铁路枢纽利用编组站解体到达列车、编组始发列车,实现“列流”向“车流”转变。除此之外,枢纽内分布有大量为城市、居民和仓库区服务的公共货运站,为工矿企业或工矿区服务的工业站,主要承担货物装卸功能,故称为装卸站。公共货运站或工业站等装卸站主要负责货物的装车和卸车工作,完成“车流”和“货流”的转换。
铁路枢纽的货流由通过流和本地流组成,其中通过流仅需办理有调和无调中转作业,而本地流则除此之外还要办理面向装卸站的作业车取送。据我国几大枢纽所在铁路局的货流统计数据,本地流作业量占到货流总量的比例均达到一半以上。
小运转作业系统是枢纽内本地货物运转的主要运输动力,承担着枢纽编组站与装卸站之间的“列流-车流-货流”转变过程中发挥着桥梁和纽带作用。其任务核心是安排枢纽小运转列车,将编组站解体后的本地作业车送往装卸站,并将完成装卸工作的本地作业车取回编组站。小运转货物作业系统在枢纽货车集结和疏散过程中发挥着不可替代的作用,直接影响枢纽运送货物的时效性。
铁路货物运输组织的相关研究较多聚焦在服务通过流的路网干线大运转列车,而服务本地流的枢纽小运转列车因为等级低、服务性强等原因,造成相关研究工作开展不足。面向铁路枢纽地方货物流的小运转作业系统受多种因素影响,最显著的特点是到达车流随机性大、可控性小,列车编组和机车运用灵活,货车在枢纽内作业次数多、停留时间长,加上小运转列车等级低、为其它列车的服务性强,从而给小运转作业系统的组织工作造成不利影响。同时,这也为小运转作业系统研究工作开展的迫切性提出了更为紧迫的要求。
针对货物作业车取送优化,Guo 等[1]以调车机车的运行和等待时间最小化为目标,研究了货物作业点取送车作业优化问题,设计了模拟退火算法进行求解。Li 等[2]利用Arena平台构仿真模拟了不同铁路专用线作业车取送-调移策略,并进行了对比分析。Yan 等[3]研究了海铁联运模式下的集装箱取送问题。Hu 等[4]研究了铁路枢纽内的货物取送径路优化问题,设计了一种动态滚动平面算法进行求解。Otto等[5]研究了技术站列车分配站场时的列车运行优化问题,以不同站场作业调车数量最少为目标构建线性混合整数规划模型。Lubbecke 等[6]研究了工厂内铁路专用线取送车调度优化问题,以取送车作业时间总和最少为目标构建混合整数规划模型,并采用分支定价算法对模型进行求解。王旭坪等[7]研究了多行程带补货时间窗的成品油配送问题,引入行程池的概念,设计了包含内外两层循环的启发式算法。葛显龙等[8]研究了跨区域多配送中心多车型开放式动态联合送货问题,建立考虑车载率的开放式车辆路径模型,给出“初始优化+实时优化”的两阶段求解策略。Bettinelli 等[9]研究了城市物流系统中带客户和中间设施时间窗要求的多程分离式货物取送问题,并提出了分支-切割-价格算法。Alyasiry等[10]研究了带时间窗和后进先出装载要求的货物取送问题,并构建了一个松弛网络流模型,并设计了一个精确求解算法。Sun 等[11]研究了以碳排量最小化为目标函数的多车型车队货物取送问题,提出了基于集划分模型的精确求解算法。Gyorgyi 等[12]研究了动态随机货物取送问题,分析了不同客户间货物取送作业发生的概率,并提出了一种基于概率分析的启发式求解算法。Zhang 等[13]等研究了面向快时尚零售商的多品种货物同步取送问题,构建了问题模型,并提出了一种元启发式算法。Boysen 等[14]研究了一类转运场铁路专用线取送车调度问题,提出一种启发式算法和分支定界算法。Chen 等[15]建立了一种基于Petri 网络的仿真网络模型,分析了多场站间铁路专用线的不同列车取送作业环节。Adlbrecht 等[16]针对调车场专用线取送车径路选择问题,建立了一种自动化决策系统,并通过仿真过程进行了效果验证。唐春林等[17]研究了一类树枝形铁路专用线直达货物列车动态取送问题,以取送车走行时间和等待时间之和最小为目标建立数学模型。程磊等[18]针对铁路树枝型专用线取送车问题,以调车取送作业总走行时间最小为目标构建0-1 规划模型,并提出一种基于元胞自动机的改进蚁群算法。李冰等[19,20]以调机作业成本和货车运营成本最小化为目标,研究了不同环境下铁路枢纽树枝形铁路专用线取送车问题,并设计了启发式求解算法。
现有研究工作主要集中在基于汽车运输的货物取送问题。面向铁路枢纽地方货物流的小运转列车取送研究相对较少,且多为单调机作业、先送后取模式。本文研究一类多调机、同步取送环境下的树枝形铁路专用线网络非直达车流取送车优化问题。以调机运营、货车运营和货车待送待取总费用最小化为目标,构建数学模型,并设计一种三阶段融合求解策略(Integrated approach with three stage,简称IA-TS)。第一阶段,首先随机生成初始取送作业顺序集合,进而利用模型起作用约束组进行更新;第二阶段,提出IBH-GA 启发式迭代寻优过程,完成对取送作业顺序集合的进一步优化;第三阶段,给出利用基于走行时长-批次时间窗的调机自适应分配策略,实现取送作业批次划分与调机分配。最后设计多组实验场景进行方法测试和结果分析。
1 问题建模
1.1 问题描述
本文研究一类小运转列车在树枝形铁路专用线网络中进行货物取送的问题。以调机运营成本、货车运营成本、货车编组站待送成本和货车装卸站待取空费成本等各项费用最小化为目标,考虑取送顺序、装卸能力、调机牵引定数、车组取回-挂运列车匹配、调机走行、取送作业时间间隔、调机-作业匹配、作业-批次匹配等限制条件,确定合理的取送批次、顺序与调机分配方案。本地货物作业车取送作业如图1所示。

图1 本地货物作业车取送过程Figure 1 Process of taking-out and placing-in local wagons
结合铁路枢纽小运转货物作业工作实际,对问题进行如下约定:多台调机并行作业,各调机的牵引定数均相同;每个取送批次既包含取车作业也包含送车作业;枢纽内专用线和装卸站分布、装卸站间调机走行时间和各车组的装卸时间均已知。
1.2 符号变量
为构建模型,研究引入以下参量与变量:
(1)集合
I:铁路枢纽内装卸站集合,记为I=,i=0 时表示编组站,时表示装卸站,为铁路枢纽内装卸站总数。
G:陆续到达编组站的车组编号集合,记为G={g∣g=1,2,…,},表示车组总数。
M:陆续到达编组站的车组的货车数,记为M={m(g)∣g=1,2,…,}。
K:调机编号集合,记为K={k∣k=1,2,…,},为调机总数。
U:取送批次编号集合,记为U={u∣u=1,2,…,},为取送批次总数。
R:陆续到达编组站的列车编号集合,记为R={r∣r=1,2,…,},其中为货物列车的总数;
H:取送作业性质集合,记为H={h∣h=1,2},h=2 表示送车,h=1 表示取车。
W:取送作业集合。用自然码标记G中各车组的送车和取车作业,记为W={w∣w=1,2,…,},为取送作业总数。
ζ(w):作业w的属性标记集合,记为ζ(w)={wI,wG,wM,wK,wU,wR,wH}。wI为作业w的目的装卸站i,wG为作业w对应车组的编号g,wM为作业w对应车组g的货车数m,wK为作业w分派的调机编号k,wU为作业w所处的批次编号u,wR为作业w对应车组到达编组站所跟随的货物列车r,wH为作业w的取送性质h。
(2)参数
hcl:调机牵引定数。
Tk:调机k的最长走行时间。
psti:装卸站i的装卸能力。
c1:单位时间调机使用成本。
c2:单位时间货车运行成本。
c3:单位时间货车等待成本。
tij:装卸站i到装卸站j的走行时间。
tw:车组wG在目的装卸站完成装卸作业所需时间。
(3)状态变量
qu:第u批次的货车总数量。显然qu=。
τu:第u批作业的取送总时间。
(4)决策变量
yuk:批次-调机匹配变量。yuk=1 表示第u批次由调机k服务,否则yuk=0。
zuw:批次-作业匹配变量。zuw=1 表示作业w属于第u批次,否则zuw=0。
(5)取送顺序表述
S(W):取送位次集合,记为S(W)={s(w)∣s(1),s(2),…,},s(w)表示作业w的取送位次。
X(W):取送顺序集合。根据取送位次S(W)的先后顺序重新排列作业W形成取送顺序集合,记为X(W)={w∣w∈W}。
1.3 模型构建
以调机运营成本、货车运营成本、货车待送待取成本最小化为目标函数,考虑取送顺序、装卸能力、调机牵引能力、车组取回-挂运列车匹配、调机走行、取送作业时间间隔、调机-作业匹配、作业-批次匹配等实际约束,建立数学模型:
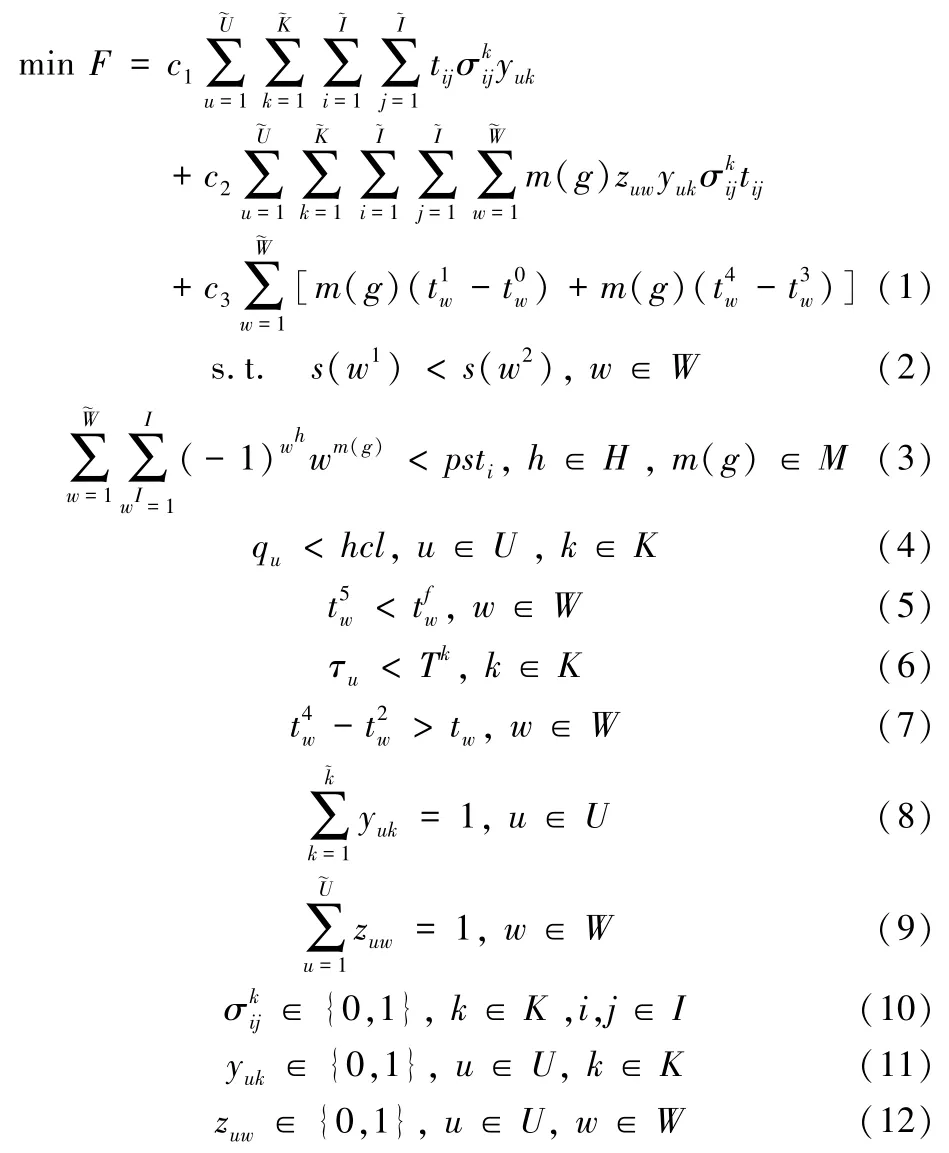
式(1)表示在站停留车小时费用和调机取送费用之和最小;式(2)表示同一组货车要先送后取;式(3)表示一个装卸站内同时作业的货车数量不能超过装卸站的容车能力;式(4)表示同批次货车数不能高于调机牵引定数;式(5)表示车组取回时间时刻必须在挂运列车最晚编组时刻前;式(6)同批次总作业时间不能高于调机最大作业时间;式(7)表示车组送车时刻和取车时刻的时间差要大于车组装卸时间;式(8)表示每批作业只能由一台调机来完成;式(9)表示每项作业不能分割,仅能划归同一批次;式(10)~(12)为变量取值约束。
2 优化求解策略
该模型为混合整数规模模型(Mixed integer programming model,简称MIP 模型),直接求解较为困难,设计取送顺序集合生成-取送顺序集合优化-调机自适应分配三阶段融合求解策略(Integrated approach with three stage,简称IA-TS)。具体步骤如下。
2.1 基于起作用约束组的初始取送作业顺序生成
首先将编组站中某一时间段内到达的车组依次用自然码进行编排,进而选取模型中制约取送作业顺序式(2)~(6)组建起作用约束组,并按照先顺序、后批次的更新策略对取送顺序进行更新,从而形成初始取送作业顺序集合。基于可行约束的初始取送作业顺序集合生成过程如图2 所示。
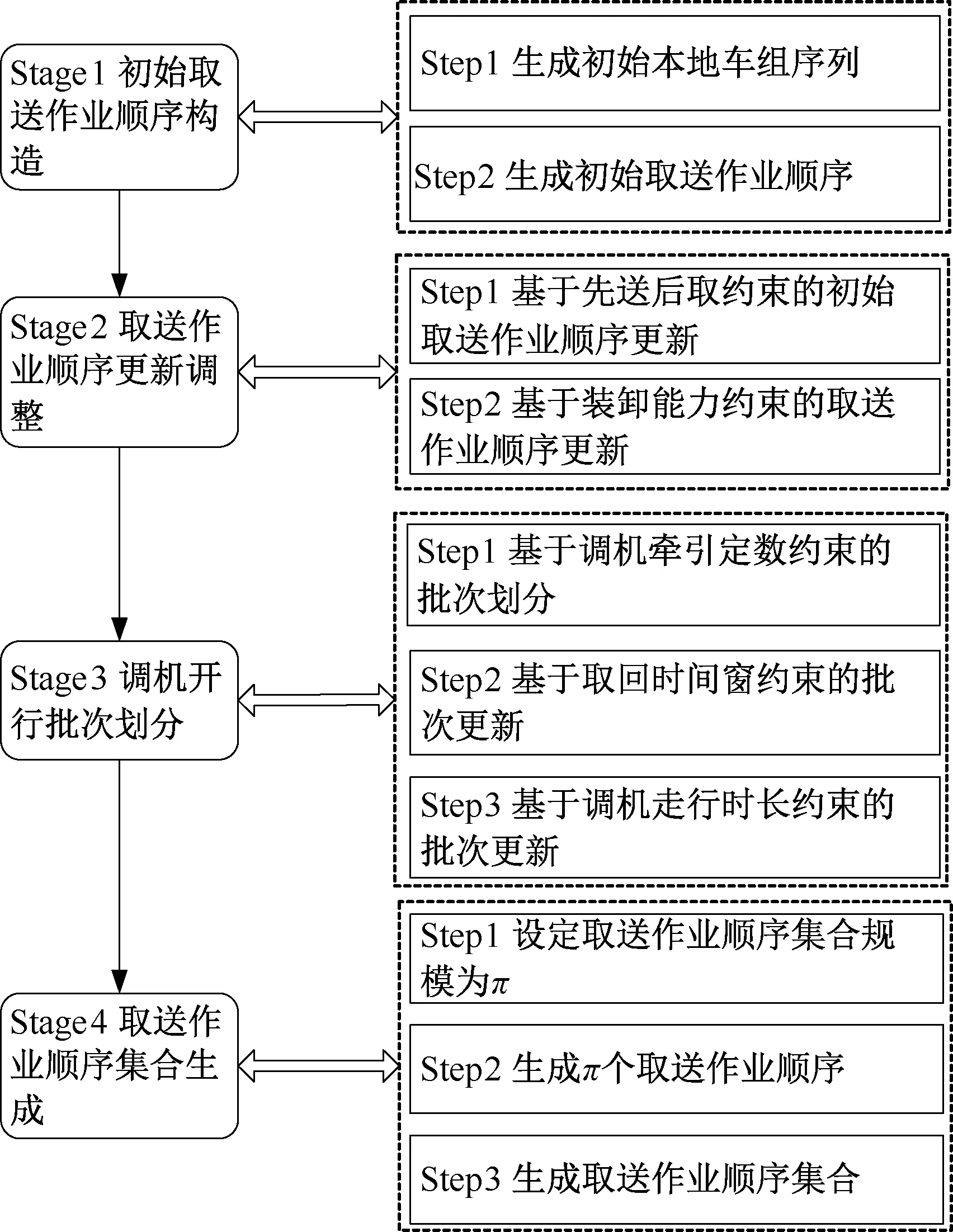
图2 基于起作用约束组的初始取送作业顺序集合生成Figure 2 Generating initial placing-in and taking out wagons sequence set using active constraint group
Stage1初始取送作业顺序构造
Step1.1生成初始本地车组序列。将编组站中某一时间段内到达的车组依次用自然码进行编排,记为G={1,2,…,},表示车组总数。
Step1.2生成初始取送作业顺序。由于各个车组在装卸站内的作业分为取车和送车两种,故用自然码对其进行编号,记为W={w∣w=1,2,…,},为取送作业总数。利用车组的初始编号生成初始取送位次集合S(W),进而得到初始取送作业顺序X(W)。初始取送顺序如图3 所示。
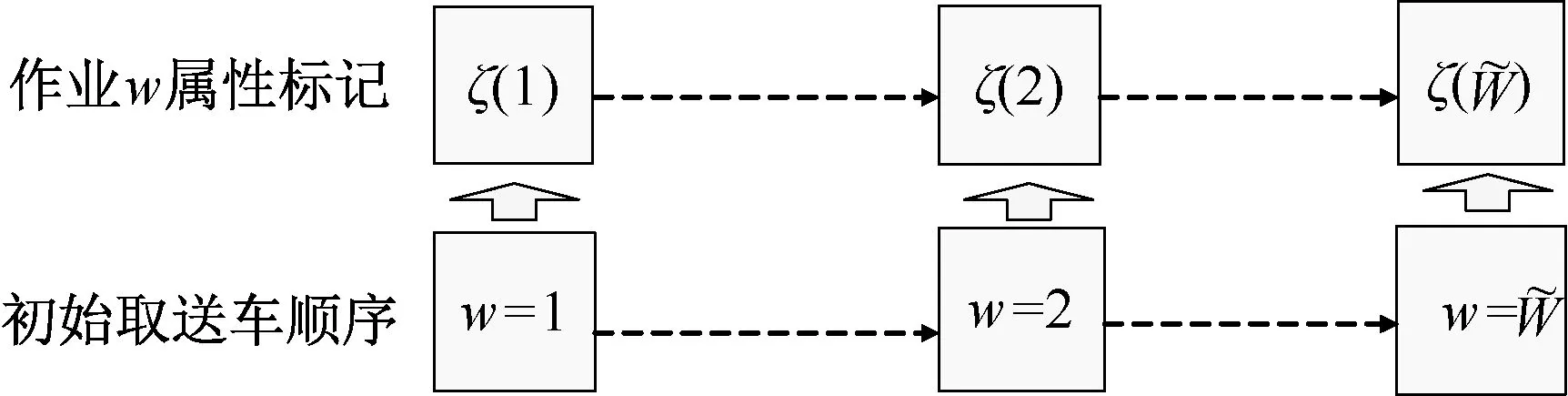
图3 初始取送作业顺序的构造Figure 3 Setting up initial placing-in and taking out wagons sequence
Stage2取送作业顺序更新调整
对初始取送顺序依据先送后取顺序限制-装卸能力限制再进行更新调整。
Step2.1基于先送后取约束的初始取送作业顺序更新
依据同一车组的不同作业先送后取的顺序限制对取送顺序进行更新,对同一车组不同取送作业w1和w2,要求取送位次s(w1)<s(w2),进而保证同一车组的送车作业一定在取车作业前面。
Step2.2基于装卸能力约束的取送作业顺序更新
利用式(3)对取送作业进行顺序调整。首先依次对各个装卸站的装卸能力psti进行检验,锁定不满足装卸能力约束的两项作业,分为两种情况:
情况一:若某一车组的送车作业与另一车组的取车作业相连,则将该车组的送车作业和该车组送取车作业顺序进行互换。
情况二:若为相邻两项送车作业,则将前一车组的取车作业与后一车组的送车作业顺序互换,得到局部调整方案。
Stage3调机开行批次划分
通过对初始取送作业顺序的调整,尚不能保证满足调机牵引定数、货车取回时刻和调机走行时长的限制,需要按照要求再进行批次更新,形成可行的取送作业顺序方案。
Step3.1基于调机牵引定数约束的批次划分
利用式(4)进行批次的划分,首先将作业按照顺序进行编排,若到某个作业顺序编号,牵引量达到调机的牵引定数,则在此位置后面插入0 进行标记,形成批次。依次对所有取送作业顺序的标记,完成批次划分。
Step3.2基于取回时间窗约束的批次更新
根据急用先送先取得原则,利用式(5)对取送作业顺序进行更新,根据批次的发车时间以及走行时间进行计算,对于不满足取回时间窗约束取车作业,往前提一个位置,再进行判断,直至满足取回时间窗的约束,依次完成批次更新。
Step3.3基于调机走行时长约束的批次更新
利用式(6)对批次进行再更新。首先统计第u批次的任务总的运行时间,若第u批次任务的总运行时间大于调机的走行时间,则此方案不满足条件,返回step3.1 再次进行批次的划分。反之,接受此方案,完成一个取送作业顺序的批次划分。
Stage4取送作业顺序集合生成
Step4.1设定取送作业顺序集合中的取送作业顺序数为π。
Step4.2重复上述步骤,产生π个取送作业顺序。
Step4.3对重复得到的取送作业顺序进行基于作业编号的调整,从而生成初始取送作业顺序集合X,表示为X=[x1,…,xπ]T,xi为一个取送作业顺序解。
2.2 基于IBH-GA 的取送作业顺序集合优化
设计嵌入遗传机制的改进蝙蝠启发式迭代寻优过程(Improved bat heuristic with genetic algorithm,简称IBH-GA)。该过程在每次迭代中,先基于蝙蝠算法更新机制对初始取送作业顺序进行改进。为防止陷入局部最优,引入遗传算法中的精英交叉机制,以提高算法全局搜索能力,最后利用终止规则完成循环迭代,得到最佳取送作业顺序,IBH-GA 算法过程如图4 所示。具体步骤如下:
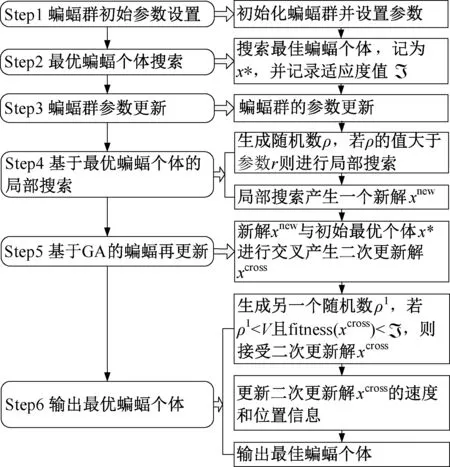
图4 IBH-GA 算法流程图Figure 4 Flowchart of IBH-GA algorithm
Step1蝙蝠群初始参数设置
将初始取送作业顺序集合中π个取送作业顺序作为蝙蝠个体,形成初始种群xbat,并设置参数初始蝙蝠脉冲发射响度Vti、蝙蝠脉冲速率ri、蝙蝠脉冲搜索范围[fmin,fmax],最大迭代次数nc_max。
Step2最优蝙蝠个体搜索
根据适应度值函数计算出初始蝙蝠群中所有个体的适应度值,选择最小的适应度值作为初始种群中最优蝙蝠个体记为x*,其适应度值为。
Step3蝙蝠群参数更新
蝙蝠脉冲频率、速度以及位置的更新公式分别为:
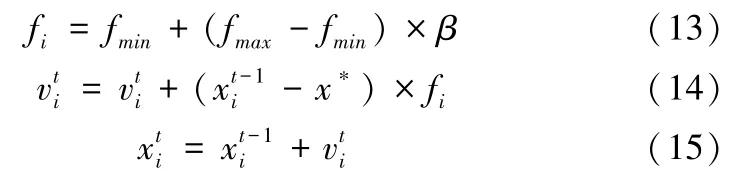
式(13)中的fi为蝙蝠个体i的搜索脉冲频率,fmax和fmin分别为其最大和最小取值,β为脉冲频度增强系数,其取值区间为[0,1];别表示第t次和t-1 次迭代过程中,第i个蝙蝠个体的速度信息;分别表示第t次和t-1次迭代过程中,第i个蝙蝠个体的位置信息。
Step4基于最优蝙蝠个体的局部搜索
生成一个均匀分布随机数ρ,若ρ>ri,则利用式(16)对最优解x*的进行局部搜索,产生新解记为xnew。
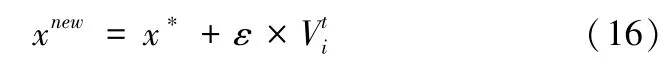
其中,ε为随机数且ε∈[-1,1]。根据蝙蝠种群更新特点,若fitness(xnew)<fitness(x*),则更新最优解xbest=xnew。
Step5基于GA 的蝙蝠群再更新
蝙蝠群的更新机制使得其易陷入局部最优陷阱,为改善此种情况,引入遗传算法的交叉机制,丰富种群的多样性。交叉方式如下:
随机取出最优蝙蝠个体xbest中一段基因,并将初始蝙蝠群中所有个体做基因冲突检测,并把这段基因插入蝙蝠群中每一个个体后面,完成交叉操作,形成新的蝙蝠群xbat1。
计算新的蝙蝠群xbat1的适应度值,找出最优的解,记为xcross。
Step6输出最佳蝙蝠个体
生成一个随机数,记为ρ1,若ρ1<Vi且fitness(xbest)<fitness(xcross),接受新解xcross为最优解,再根据式(17)和式(18)对xcross更新频率ri和响度的信息:
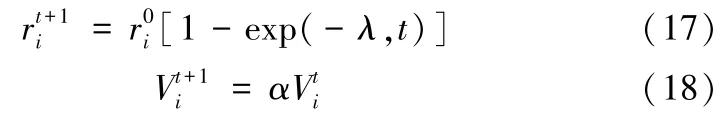
式(16)中α和λ分别为脉冲音强衰减系数和脉冲频率增强系数,α、λ∈[0,1]。
Step7迭代终止条件
返回Step3,重复迭代。若迭代次数达到nc_max,则停止迭代,输出最优解及对应最佳取送作业顺序,并记录随迭代次数的变化曲线。
2.3 基于批次时间窗-走行时长的调机自适应分配
铁路枢纽内的取送作业往往需要多台调机共同完成,从而给出调机自适应配置过程(Engine Adaptive allocation procedure,简称EAAP)。该过程以取送时间窗限制及最小化调机数为基本原则,对IBH-GA 得到的最佳取送作业顺序,计算每批次的时间窗,为每批次取送任务配置一台调机。当前调机无法满足取送批次时间窗要求或达到调机最长走行时间限制时增加新调机,从而实现枢纽内的调机对取送作业的动态配置。基于批次时间窗-走行时长的调机自适应分配流程如图5 所示。
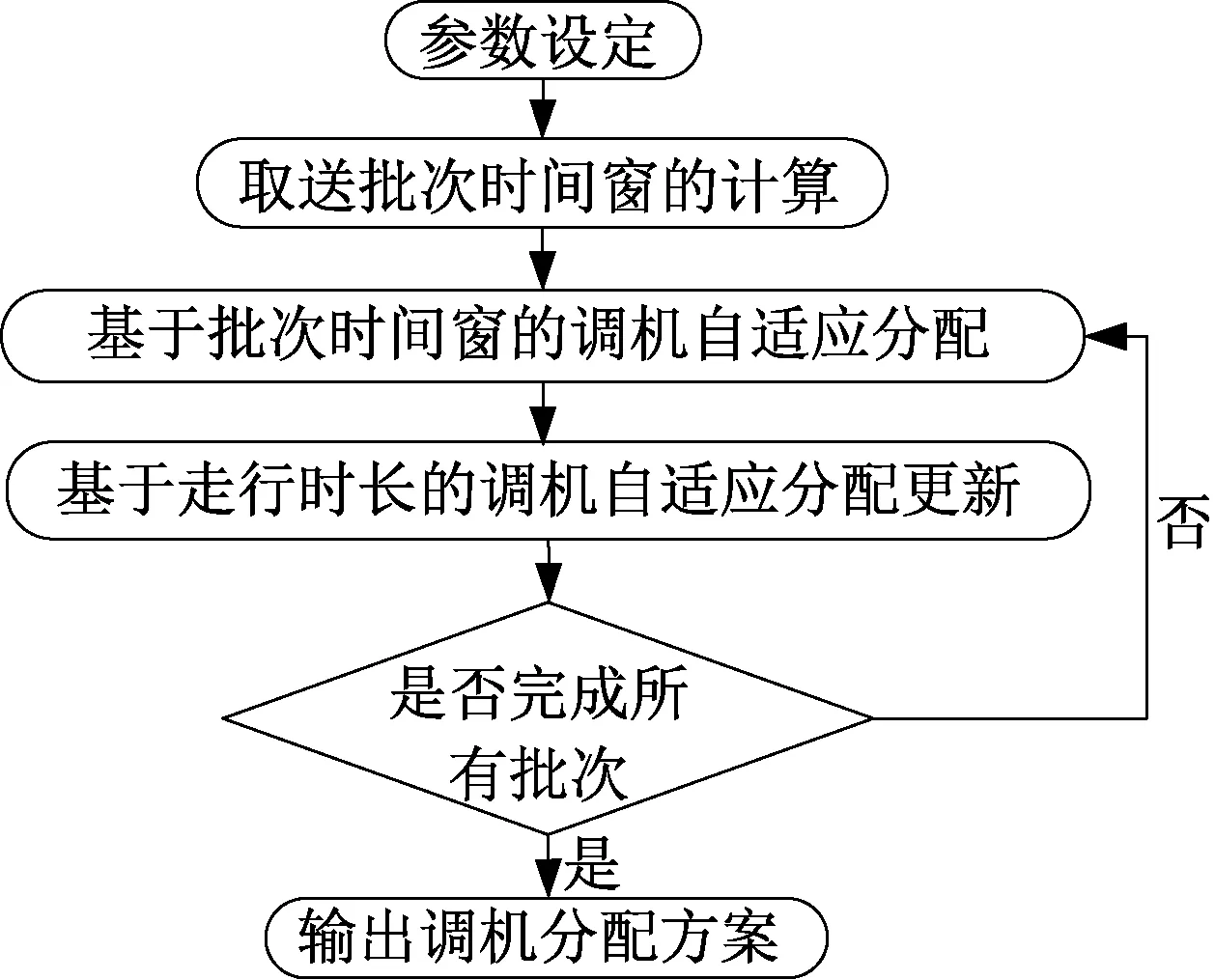
图5 基于批次时间窗-走行时长的调机自适应分配Figure 5 Flowchart of engine adaptive allocation procedure considering batch time windows and engine running time
Step1参数设定。
调机最长走行时间为Tk,调机编号集合K={k∣k=1,2,…,},其中为调机总数,取送作业批次编号集合U={u∣u=1,2,…,},其中为取送作业批次总数。
Step2取送批次时间窗计算
根据IBH-GA 优化得到取送顺序批次方案的发车时间、返回编组站时间,并设立时间窗。其中表示第u批次取送作业的发车时刻,表示第u批次取送作业返回编组站时刻。
Step3基于批次时间窗的调机自适应分配
依据批次分配方案进行调机分配,调机分配策略:首先对批次u=1 的任务分配编号为k=1 的调机,再对批次u=2的任务进行调机的分配,此时要判断调机k=1 是否已经回到编组站,若调机k=1 没有回到编组站则启用调机k=2。依次对所有批次进行调机的分配,直至完成所有的批次任务。
Step4基于走行时长的调机自适应分配更新
对满足时间窗约束的调机k再基于调机走行限制进行更新。τu表示第u批次完成取送所需要的时间,τu=。若k=1 满足时间窗,但(τ1+τ2)>T1,那么启用调机k=2 完成下一批次的取送任务;若k=1 满足时间窗,但(τ1+τ2)<T1,分配调机k=1 完成下一批次的取送任务。
Step5输出调机分配方案
依次完成所有批次的取送任务,得到调机分配方案,完成调机自适应分配。
3 实验验证及结果分析
3.1 实验场景
(1)树枝形铁路专用线网络
设计一个树枝形铁路专用线网络,其中0 表示编组站,1~12 表示装卸站,如图6 所示。各装卸站间的调机走行时间如表1 所示。
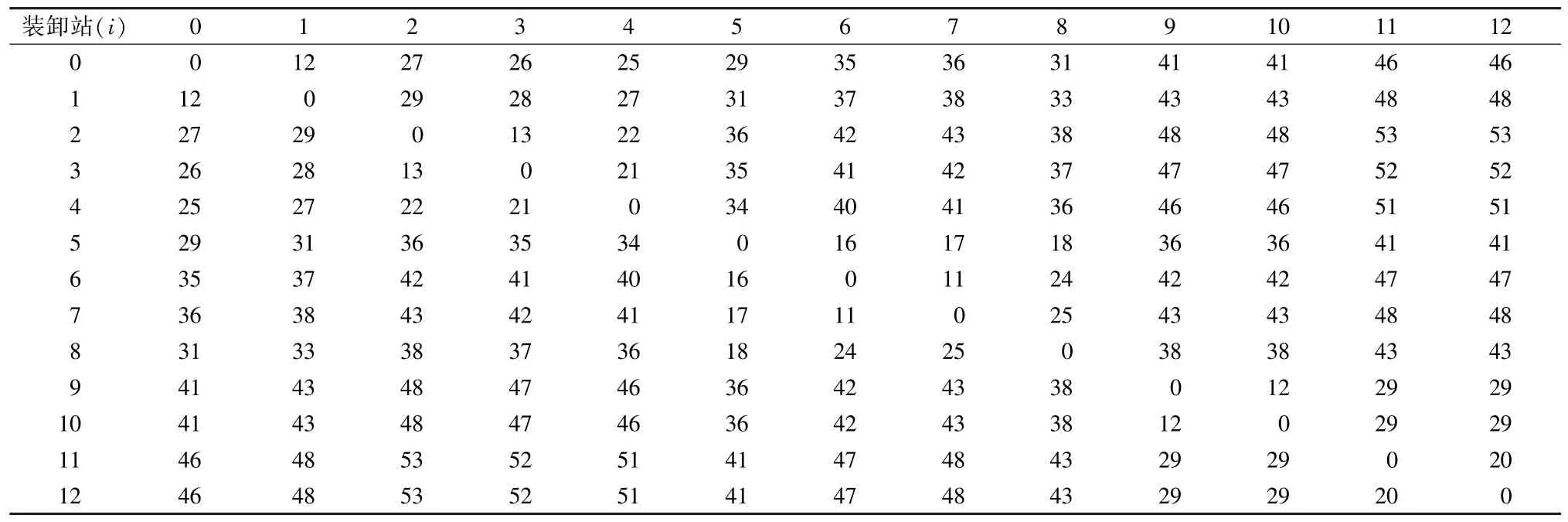
表1 各装卸站之间的调机走行时间(单位:分钟)Table 1 Running time of shunting engine between handling stations in railway terminal (Unit:min)
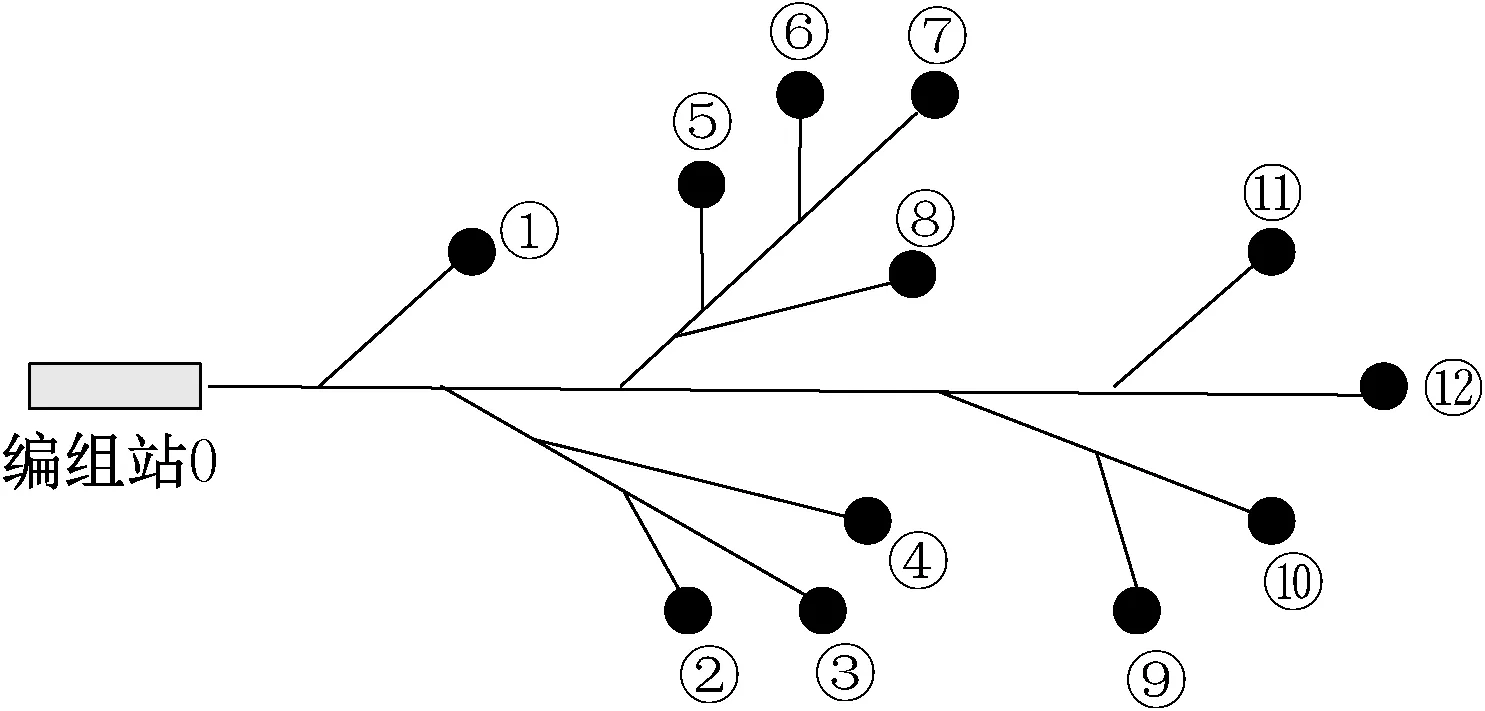
图6 铁路枢纽树枝形专用线Figure 6 Branch-shaped siding in railway terminal
(2)枢纽内车流到达信息
在编组站内,陆续有4 列货物列车到达,根据货车的目的地不同将货车分为16 个车组,由于各车组在装卸站中作业方式包含取车作业和送车作业,将16 个车组分为32 个取送作业并用自然码进行编号,记为W={w∣w=1,2,…,32}。车流数据如表2 所示。
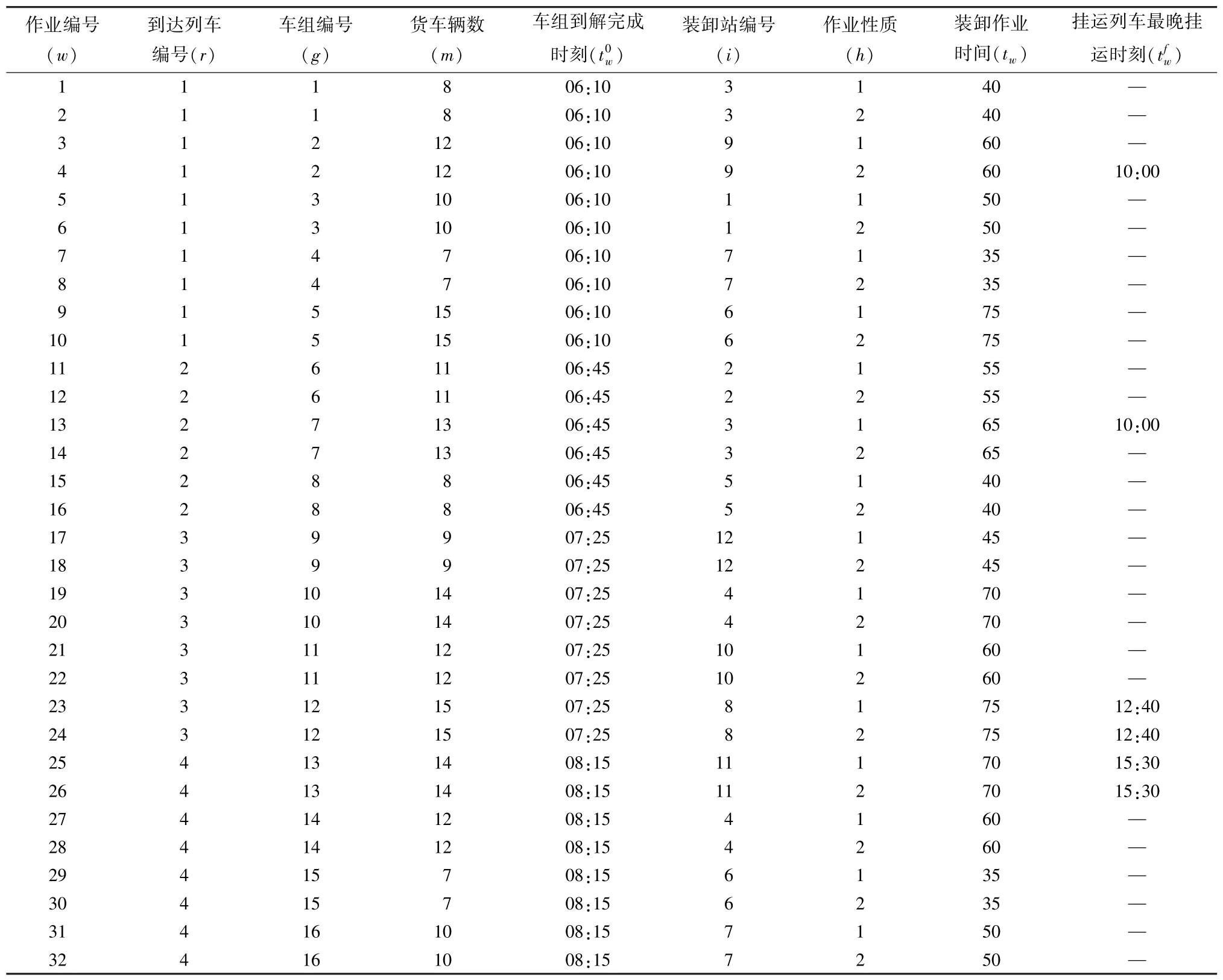
表2 作业车取送信息表Table 2 Data of arrival train and wagon flow in railway terminal
(3)装卸站的装卸能力信息
12 个装卸站由于货物线长度限制,每个装卸站都有最大装卸能力,网络内所有的装卸站以及装卸能力信息如表3所示。

表3 装卸站装卸能力Table 3 Handling station capacity
3.2 IA-TS 主要参数的调试
IA-TS 采用试算法来确定主要参数值。利用Matlab R2014a 对 IA-TS 求解算法进行编程,在Windows 7 作为系统,处理器为Intel(R) Core(TM) i5-4200 M CPU @ 2.50 GHz 微机上运行,选取IA-TS 中对结果影响较大的蝙蝠脉冲发射响度V和蝙蝠脉冲频率r两个参数进行测试。测试方法为固定其中一个参数,调整另一个参数,基于多种参数组合进行尝试,找出最优参数组合。
根据以往参考文献数据,设定调机单位分钟运营成本c1=16、货车单位分钟运营成本c2=1.2、货车单位分钟待取待送成本c3=8、调机最大牵引定数hcl=40、调机最大行驶时间Tk=300 min。设定IA-TS 算法中的固定频率f_min=0、f_max=1、α=0.9、λ=0.9,蝙蝠群数量π为10,交叉概率取0.9,最大迭代次数nc_max=300,给出蝙蝠脉冲发射响度V和蝙蝠脉冲频率r参数取值如表4 所示。

表4 IA-TS 求解算法的参数设置Table 4 Parameter setting for IATS approach
根据参数设置,生成25 组参数,分别测试每组参数对运营成本及CPU 运行时间的影响,每组参数测试十次并将结果取平均值,不同参数组合下求得运营成本和CPU 运行时间如表5 所示。
从表5 中可以看出:蝙蝠脉冲发射响度V对于营运成本和CPU 运行时间的影响没有呈现出一定的规律性,这说明蝙蝠脉冲发射响度V对解的影响具有随机性。蝙蝠脉冲频率r的增大会减少CPU 运行时间,但对解的质量影响没有呈现规律性。通过结果的对比,选取V=0.95、r=0.3 为最优参数组合。

表5 不同参数组合下IA-TS 求解算法运行结果对比Table 5 Comparing results for IA-TS under different parameters setting
3.3 算法比对方案设计
在解决排序问题上,遗传算法GA 和蝙蝠算法BA 相较传统算法表现出更为突出的性能优势。故引入此两种算法作为比对,以验证本文所提出的IA-TS 方法的计算性能。
又因GA 和BA 仅能优化取送作业顺序,无法进一步完成调机指派,从而引入文本提出的调机自适应配置过程(EAAP)来实现。故将此两种比对算法简写为GA-EAAP 和BA-EAAP。
3.4 过程验证
按照3.2 节得到的最优参数组合对IA-TS 算法进行配置:固定频率f_min=0,f_max=1,α=0.9,λ=0.9,蝙蝠群数量π为10,交叉概率取0.9,最大迭代次数nc_max=300,蝙蝠脉冲发射响度V=0.95,蝙蝠脉冲频度r=0.3;BA-EAAP 算法的参数与IA-TS 求解算法的保持一致;GA-EAAP 算法交叉概率取0.9,变异概率取0.05。算法运行结果如表6 所示。
利用表6 中取送位次s(w)的顺序,我们可以得到取送作业顺序。例如表6 中GA-EAAP 算法中作业w的取送位次:s(w)={s(1)=1,s(7)=2,s(5)=3,…,s(6)=32},可以得到取送顺序x={1,7,5,…,6},再根据得到的取送顺序以及表6 中的批次信息、表1 的装卸站间的调机走行时长和表2 的取送车组作业信息表可以得到作业所属批次、批次的发车时刻和各个批次取送作业的总时长,以批次的发车时刻和完成时刻设置时间窗,并基于批次时间窗和调机走行时长进行调机的自适应分配,得到调机的分配方案。
对表6 的实验仿真对比结果进行分析,分析结果如下:
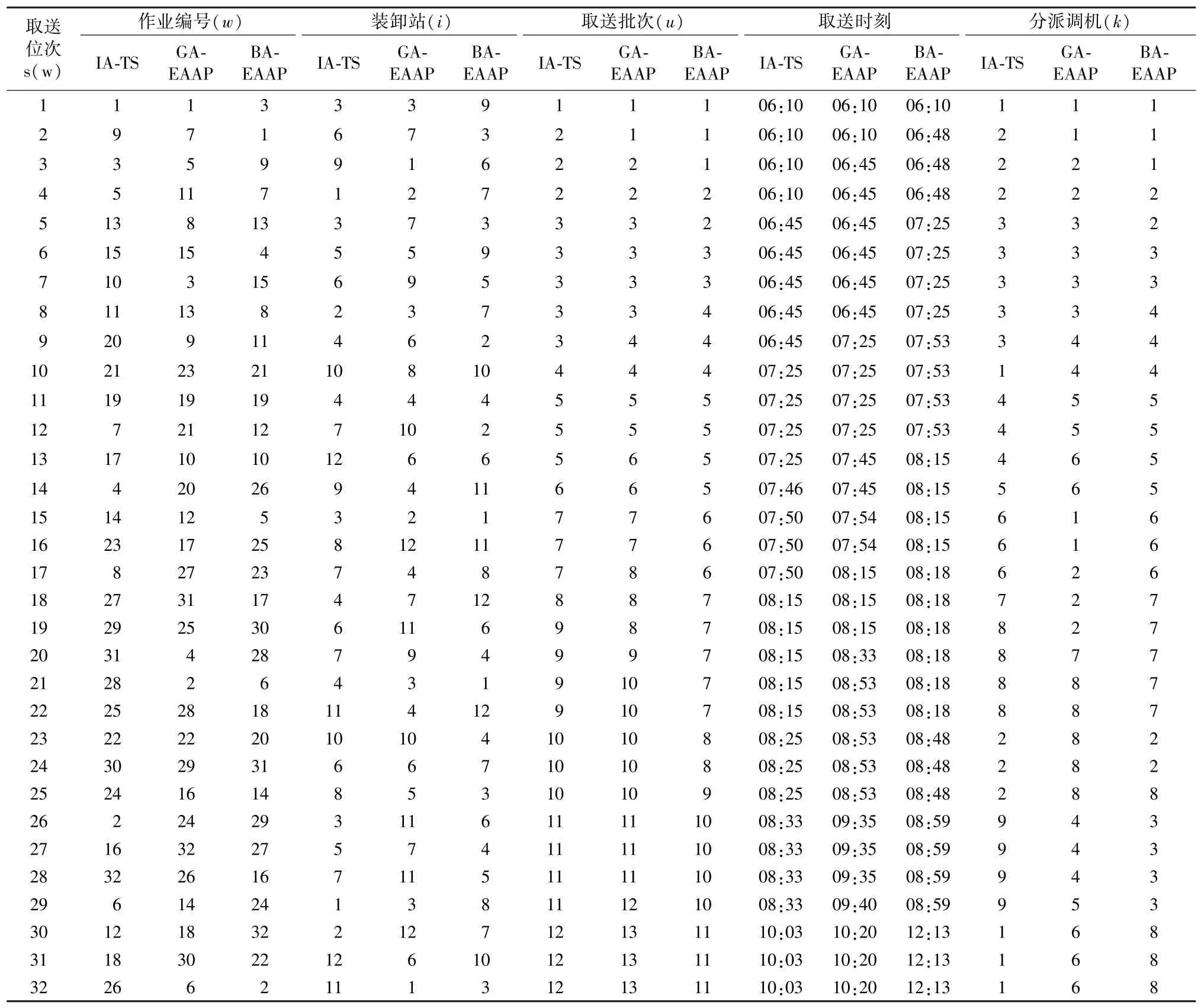
表6 IA-TS、GA-EAAP 和BA-EAAP 的运行计算结果Table 6 Results for IA-TS,GA-EAAP and BA-EAAP applied to the test
IA-TS 求解结果为0-1-0-9-3-5-0-13-15-10-11-20-0-21-0-19-7-17-0-4-0-14-23-8-0-27-0-29-31-28-25-0-22-30-24-0-2-16-32-6-0-12-18-26-0,调机走行时间为 1314 min,总营运成本为50091.2 元,调机分配方案[{u=1,k=1},{u=2,k=2},{u=3,k=3},{u=4,k=1},{u=5,k=4},{u=6,k=5},{u=7,k=6},{u=8,k=7},{u=9,k=8},{u=10,k=2},{u=11,k=9},{u=12,k=1}]。
GA-EAAP 求解结果为0-1-7-0-5-11-0-8-15-3-13-0-9-23-0-19-21-0-10-20-0-12-17-0-27-31-25-0-4-0-2-28-22-29-16-0-24-32-26-0-14-0-18-30-6-0,调机走行时间为1477 min,总营运成本为61496 元,调机分配方案[{u=1,k=1},{u=2,k=2},{u=3,k=3},{u=4,k=4},{u=5,k=5},{u=6,k=6},{u=7,k=1},{u=8,k=2},{u=9,k=7},{u=10,k=8},{u=11,k=4},{u=12,k=5},{u=13,k=6}]。
BA-EAAP 求解结果为0-3-1-9-0-7-13-0-4-15-0-8-11-21-0-19-12-10-26-0-5-25-23-0-17-30-28-6-18-0-20-31-0-14-0-29-27-16-24-0-32-22-2-0,调机走行时间为1442 min,总营运成本为91182.4 元,调机分配方案[{u=1,k=1},{u=2,k=2},{u=3,k=3},{u=4,k=5},{u=5,k=5},{u=6,k=6},{u=7,k=7},{u=8,k=2},{u=9,k=8},{u=10,k=3},{u=11,k=8}]。
三种算法调运成本随迭代次数的收敛曲线对比如图7所示。从图中也可以明显的看出:IA-TS 算法比GA-EAAP 和BA-EAAP 算法得到的解的质量更好,运营成本比较结果为IA-TS<GA-EAAP<BA-EAAP。
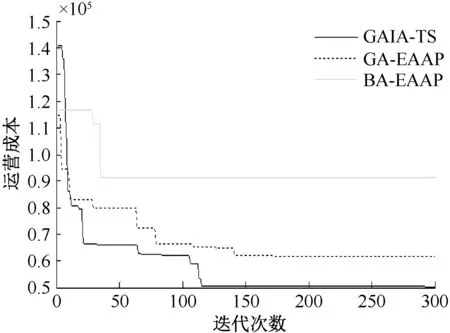
图7 三种算法调运成本随迭代次数收敛曲线对比图Figure 7 Comparison for shunting cost with iteration number for three algorithms
3.5 实验测试对比与性能评估
为了对IA-TS 算法进行性能测试和评估,本文利用图6 的树枝形专用线网络和表2 的车流信息表数据,分别设计12项取送作业、32 项取送作业和64 项取送作业等三组不同取送作业数量的实验,测试IA-TS、GA-EAAP 和BA-EAAP 算法的性能。三种被测算法的参数设置如表7 所示。

表7 三种算法的参数设置Table 7 Parameter setting for the three algorithms
本文设置迭代次数nc_max为300 次,将其作为IA-TS、GA-EAAP 和BA-EAAP 算法测试的停止条件。对每组参数{π,hcl}测试10 次,取平均目标函数值Fava、平均计算机运行时间和算法改进率RAC 作为比对参考指标。RAC 为比对算法的平均Fava之差与IA-TS 算法平均Fava的比值。RAC1为IA-TS 相对于GA-EAAP 的改进率,RAC2为IA-TS 相对于BA-EAAP 的改进率,即
RAC1=(GA -EAAPC-(IA-TSC))/IA-TSC×100%
RAC2=(BA -EAAPC-(IA-TSC))/IA-TSC×100%
测试结果如表8、表9 和表10 所示。

表8 三种算法在10 项取送作业问题中的性能测试比对Table 8 Performance for IA-TS、GA-EAAP and BA-EAAP applied to the problem with 10 placing-in and taking-out wagons

表9 三种算法在32 项取送作业问题中的性能测试比对Table 9 Performance for IA-TS、GA-EAAP and BA-EAAP applied to the problem with 32 placing-in and taking-out wagons

表10 三种算法在64 项取送作业问题中的性能测试比对Table 10 Performance for IA-TS、GA-EAAP and BA-EAAP applied to the problem with 64 placing-in and taking-out wagons
可得到如下结论:
(1)对于不同规模问题,三种算法在解的表现上有所差异,其中BA-EAAP 算法CPU 运行时间较短,求解质量较差;IA-TS 算法的CPU 运行时间较长,但求解质量最好。
在10 项取送作业问题中,IA-TS 算法的解的质量分别平均高于GA-EAAP 算法14%和BA-EAAP 算法19%;在32 项取送作业问题中,IA-TS 算法的解的质量分别平均高于GAEAAP 算法17%和BA-EAAP 算法51%;在64 项取送作业问题中,IA-TS 算法的解的质量分别平均高于GA-EAAP 算法24%和BA-EAAP 算法69%。IA-TS 相较与BA-EAPP 和GAEAAP 的改进率如表11 所示。

表11 IA-TS 算法相较于BA-EAAP 和GA-EAAP 的改进率Table 11 Improvement rate of IA-TS comparing with BA-EAAP and GA-EAAP
根据不同取送作业数量下改进率RAC1和 RAC2的平均值结果对比,随着取送作业数量的增加,改进率RAC1和RAC2是呈上升的趋势,说明作业数量增加的情况下,IA-TS算法相对于GA-EAAP 算法和BA-EAAP 算法优势更加明显。
(2)对于不同参数,可以看到在不同种群数量下,种群数量π=20 时的计算机运行时间要明显高于π=10 时候,但求解质量并没有得到明显改善,有的更是没有改善,说明增加种群数量会增加计算机运行时间,并不能提高解的质量。
3.6 求解质量与算法迭代次数的相关性
选用3.5 节的三组实验,选取3.2 节中参数调试结果中的较优参数组合{V=0.95,r=0.3}。测试算法求解质量与迭代次数的相关性,如图8 所示。由此可以看出,随着迭代次数的增加,IA-TS 算法的优势更为明显。

图8 求解质量与算法迭代次数的演进关系Figure 8 Comparison for solution quality with iteration number of algorithms under different size problems
4 结论
铁路枢纽小运转作业系统承担着本地货流运转的重要任务,其核心工作就是编排小运转列车完成枢纽内编组站与装卸站间的本地作业车取送。本文以调机运营成本、货车运营成本、货车待送待取成本最小化为目标函数,考虑取送顺序、装卸能力、调机牵引能力、车组取回-挂运列车匹配、调机走行、取送作业时间间隔、调机-作业匹配、作业-批次匹配等实际约束,建立树枝形专用线非直达车流取数学模型。鉴于直接求解较为困难,本文故设计取送顺序集合生成-取送顺序集合优化-调机自适应分配的三阶段融合求解策略。该策略在第一阶段,随机生成初始取送作业顺序集合并利用模型起作用约束组进行更新;第二阶段,利用IBH-GA 启发式完成装卸站间货车取送作业顺序优化;第三阶段,利用基于批次时间窗-走行时长的EAAP 过程实现取送作业批次划分与调机分配。最后,设计多组实验场景进行方法测试和结果分析。
铁路枢纽专用线网络主要有放射形、树枝形和混合形三种形式,本文研究了树枝形铁路专用线取送车优化问题,作业车均为单重作业车,没有考虑作业车在枢纽内不同装卸站间的调移问题。未来研究工作将聚焦更为复杂的混合形铁路专用线取送车优化,并考虑带调移的双重作业车取送问题。
