刮板输送机圆环链拓扑与响应面优化研究
2022-07-21王子升高宇杰李嘉浩王学文
梁 超,李 博,王子升,高宇杰,李嘉浩,王学文
(1.太原理工大学 机械与运载工程学院,山西 太原 030024; 2.煤矿综采装备山西省重点实验室,山西 太原 030024)
刮板输送机是综采工作面机械化生产过程中主要的运输设备,动力传动方式以链传动为主,主要部件包括链轮和链环,动力通过“链轮—链环—其他部件”的方式传递。在传动过程中,链环承担着至关重要的媒介作用。在实际工作过程中,整条圆环链是由数量庞大的链环环环相扣组合而成的,只要其中一个链环发生断裂,整个刮板输送机就必须被迫停止运行并进行维修,而巨大的链环个数使得整条圆环链发生断链的可能性大增。因此,提高圆环链的设计质量对于提高刮板输送机的生产效率和使用寿命以及减少断链事故具有重要意义。
在刮板输送机圆环链力学特性方面,何柏岩等[1,2]建立了刮板输送机圆环链传动系统的动力学模型,利用ABAQUS对圆环链进行了弹塑性接触分析,得到链环的应力场及链条的伸长率;张东升等[3]和王学文等[4]研究了启动、制动和卡链等工况下链传动系统的力学特性。在圆环链力学特性研究的基础上,诸多学者对圆环链的性能及其影响因素进行了研究。王维喜等[5]发现圆环链的链环尺寸和形状对其力学性能有显著影响;张强等[6]发现重载启动时圆环与直圆柱间的过渡部位腐蚀的链环更容易发生腐蚀断裂失效。根据李惟慷等[7]和刘治翔等[8]对刮板输送机运行阻力的分析可知,圆环链的重量直接影响到刮板输送机运行阻力的大小。这些研究为圆环链的性能和优化研究提供了理论依据和试验参考。
拓扑优化和响应面优化是设计领域中两种比较实用的优化方法。张志飞等[9]和廖莺等[10]通过拓扑优化方法实现了汽车座椅和后副车架的轻量优化设计;赵保林等[11]利用响应面法对刮板输送机中板进行了仿生耐磨优化;ISMAIL等[12]利用拓扑优化和响应面优化相结合的方法对自行车曲柄进行了优化设计。拓扑优化多用于目标结构的轻量化设计,而在结构的形状尺寸优化方面则是响应面优化方法更有优势,两者结合可以进行优势互补。
本文基于圆环链的有限元接触分析结果,应用拓扑优化结合响应面优化方法对圆环链进行优化,从而降低链环自重、减小最大等效应力和等效应变以改善圆环链接触状态。
1 有限元模型构建
1.1 建立三维模型
本文以某型号的刮板输送机为研究对象,其所用的刮板链型号为:圆环链公称尺寸∅34mm×126mm[13],中双链形式,为对称结构,故取其一侧进行分析。
本文使用NX(版本10.0)软件建立链环三维几何模型[4]。在整个运行过程中,每个链环大多数的工作时间都处于直行状态,只有少部分时间与链轮进行啮合,所以选取直行区域的链环进行分析和优化设计。为提高计算效率,从直行段选取3个链环进行三维建模,并对焊缝处进行了简化,从左到右链环依次命名为:链环1、链环2和链环3。
1.2 构建有限元模型
本文的有限元模型生成方法如下:
1)定义材料。将圆环链三维模型导入ANSYS Workbench(版本19.2),定义链环材料为23MnNiCrMo,材料的弹性模量E=210GPa,泊松比μ=0.3,密度ρ=7.8×10-6kg/mm3[14]。
2)定义接触。根据链环间的实际接触情况,定义链环间接触为“面-面”摩擦接触,摩擦系数为0.15,接触行为选择对称接触;算法选定拉格朗日算法。
3)对计算模型进行网格划分。有限元网格选择四面体网格,网格大小设置为5mm,共划分为50104个单元,共74841个节点,网格划分及其接触区域如图1所示。

图1 圆环链网格划分及其接触区域
4)施加约束载荷。在圆环链的左半环断面上施加固定约束,限制其位移,在右半环断面上施加位移约束,沿Y方向施加大小始终为200000N的拉力,设置计算时间为1s,子步数为5。
2 接触模型验证及分析
2.1 模型验证
为保证圆环链有限元模型的准确性,通过圆环链静拉伸试验对该模型进行验证。静拉伸试验参考《矿用高强度圆环链》(GB/T 12718—2009)[13]规定的C级试验条件进行,试验设备采用500t的微机控制电液伺服万能试验机,根据试验测得的链条变形量和式(1)可以得到试验载荷下链条伸长率,试验重复3次,并在Workbench中进行载荷相同的仿真。
式中,η为圆环链的伸长率,%;l0为初始长度,mm;l为试验负荷下的长度,mm。
真实试验与仿真的结果见表1,真实试验测得的链条伸长率均值为1.36%,仿真的伸长率为1.27%,真实试验与仿真的伸长率较为吻合,表明该有限元模型具有较高的可行性和准确性。
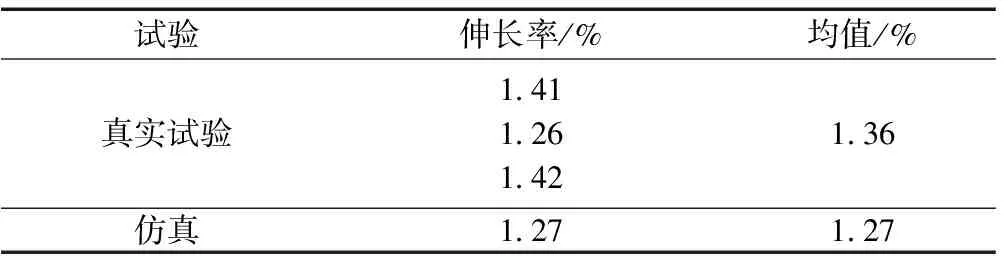
表1 真实试验与仿真的伸长率
2.2 接触结果分析
经过有限元计算,得到圆环链的链环间接触计算结果。本文的目的是以对圆环链的接触分析为基础,对圆环链进行优化设计,因此选择将完整的链环2作为研究重点,其质量为2.841kg,接触等效应力和等效应变如图2所示。
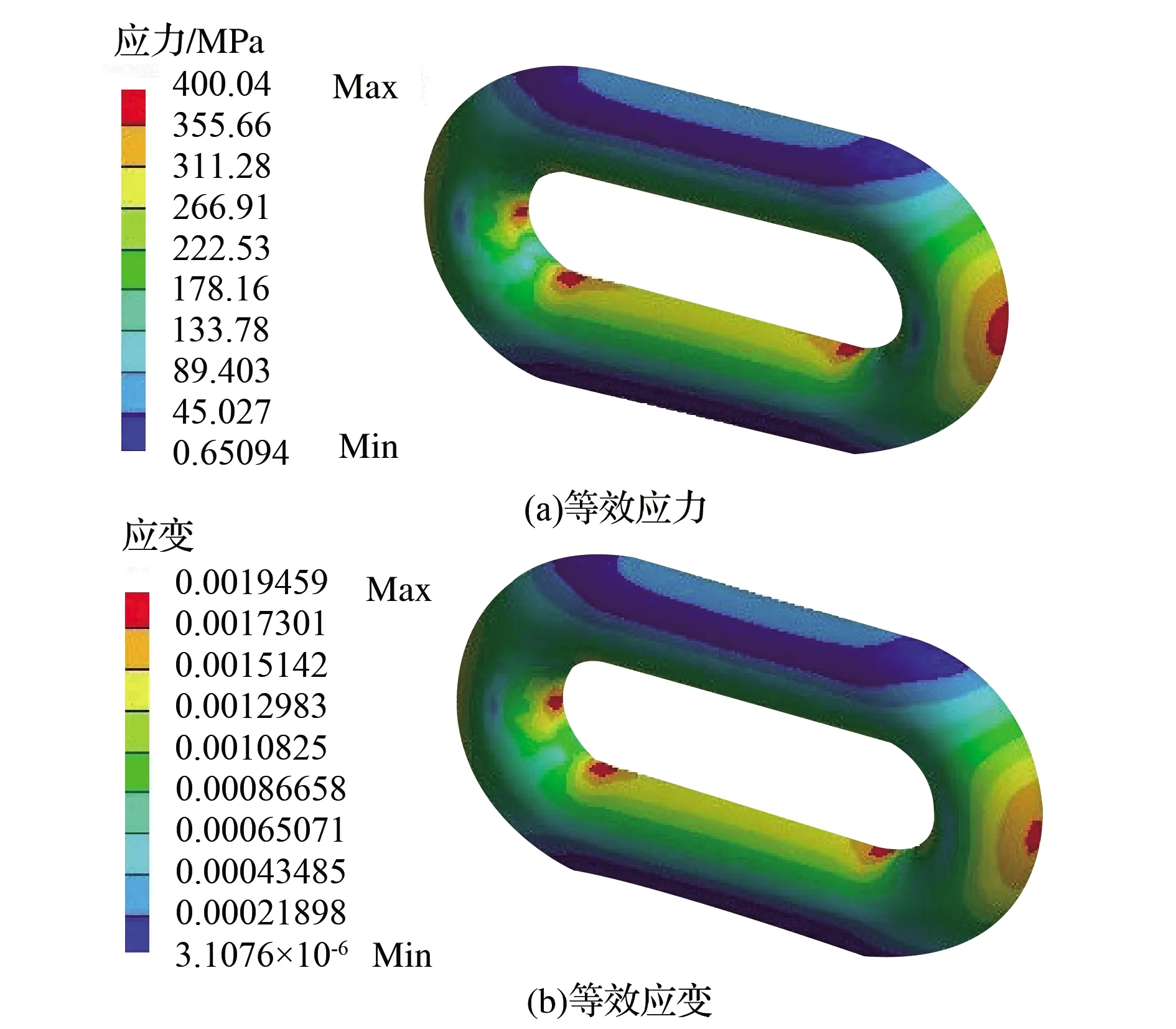
图2 链环2的接触效应力应变
由图2可以看出,链环2的等效应力和等效应变分布都呈明显的对称分布状态,等效应力和等效应变的最大值都出现在两链环的圆环内侧接触部位,最大值分别为400.04MPa和0.00195,同时在圆环链的圆环部位和直圆柱部位的连接过渡区间也存在有明显的等效应力集中现象。等效应力和等效应变从内侧到外侧呈现明显的梯度分布:内侧等效应力和应变最大,向外侧逐渐减小,到最外侧后又突然增大,最小等效应力和等效应变分别为0.651MPa和3.108×10-6,出现在链环直圆柱的中间位置。
3 链环优化设计
基于上述的圆环链接触特性分析,本文通过拓扑优化结合响应面优化对链环结构进行优化研究,优化数学模型为[15]:
式中,x=[x1,x2,…,xn]为设计变量,n为设计变量个数;fn(x)为目标函数;gp(x)为不等式约束条件,共m个;hq(x)为等式约束条件,共k个;xiu和xiv分别为设计变量xi的上边界和下边界。
3.1 拓扑优化
拓扑优化可以在不损害结构原有刚度的前提下对原机构实现轻量化设计,尽可能保留其原有的性能。在Workbench中选定优化目标为链环2的质量,边界约束沿用前文接触分析时的约束和载荷,设置链环质量分别保留85%、80%和75%,求解结果如图3所示。

图3 圆环链拓扑优化求解结果
链环直圆柱段外侧有部分被去除,删减部分质量分别为0.419kg、0.566kg和0.706kg,结合2.2节的分析可知,被删减的部分正是链环直圆柱段承受压应力作用层以及应力最小层部位。根据链环拓扑优化的求解结果,结合链环的加工难度,对链环直圆柱段外侧进行了水平削减,被削除部分的厚度为4mm。将改进的模型导入Workbench重新做静力学分析,对比改造前后链环2的接触效应,见表2。改造后链环2的质量降为2.733kg,减少了3.80%;最大等效应力为402.92MPa,增大了0.72%;最大等效应变为0.00193,降低了1.03%。
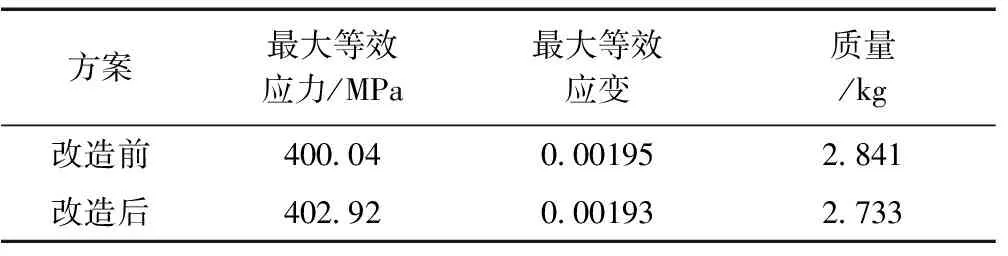
表2 改造前后链环2的接触效应
3.2 响应面优化
3.2.1 模型参数化及试验设计
为改善链环接触状态,在拓扑优化的基础上,在拓扑优化结果的基础上,对链环进行了如图4的改造:对链环直圆柱部分的外侧进行削平,以改变链环外宽半径(即削平截面距离中间对称面的距离);对链环内侧进行削减,以改变链环内宽直径(即红色圆弧直径)。然后对改造后的圆环链模型进行参数化并将参数化模型导入Workbench,按照前文所述进行前处理设置,并进行有限元求解。

图4 改造的圆环链三维模型
选择链环外宽半径和内宽直径作为设计变量,选择最大等效应力、最大等效应变作为响应面优化的目标变量。边界条件依旧沿用优化前接触分析时的约束和载荷设置。本文的试验设计选用拉丁超立方体采样设计方法,该方法的采样点均匀且不聚集,采样值在设计空间中具有较高的整体覆盖程度,提高了采样精度和效率[16,17]。样本点数设置为40个,并对设计输入参数范围进行合理的设置,见表3。设置完成后ANSYS DesignXplorer软件自动生成预试验设计点,对所有的试验设计点进行更新求解,试验结果见表4。

表3 设计变量范围设置
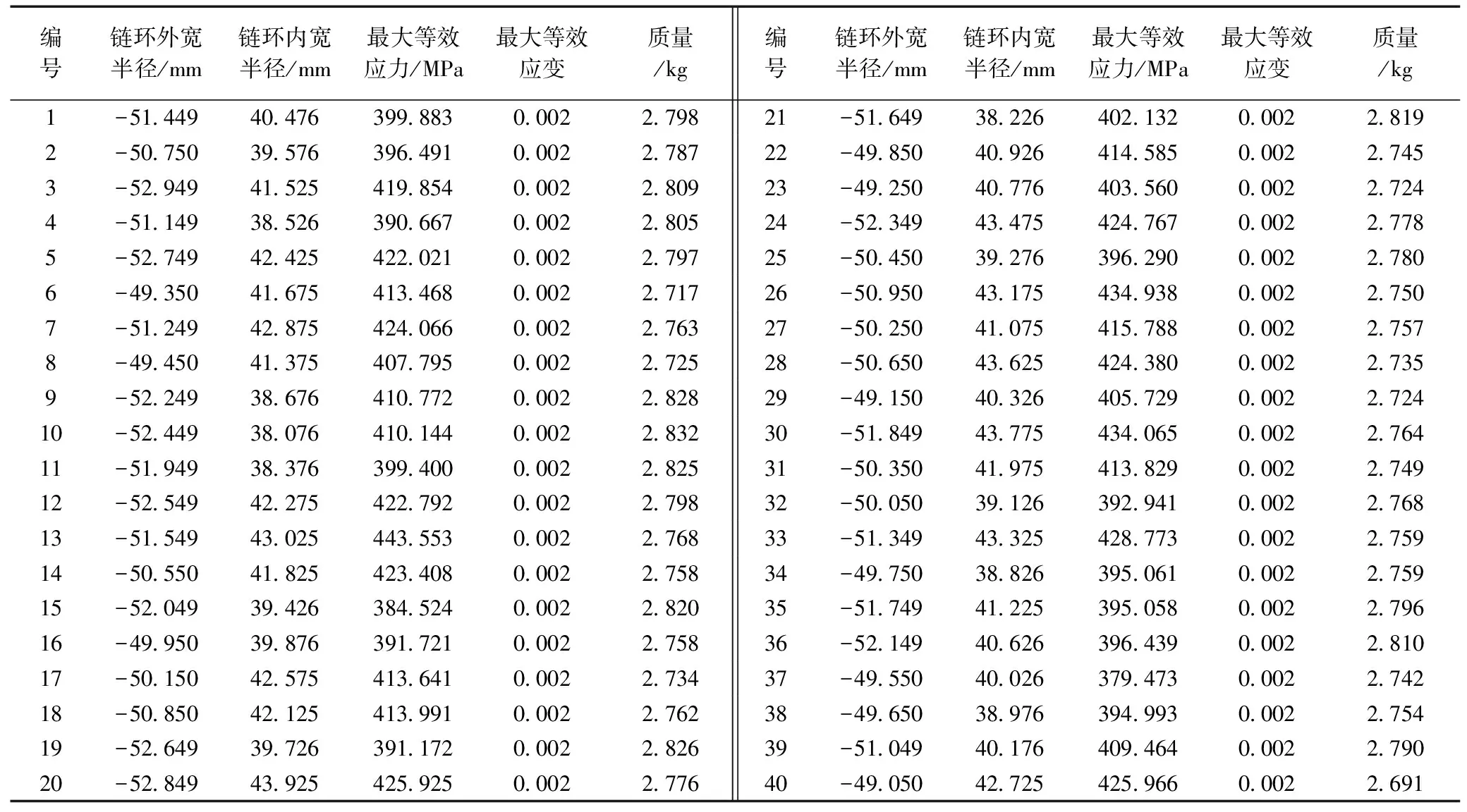
表4 试验结果
3.2.2 响应面及敏感度
根据表4的设计点试验数据,在Workbench中选用Kriging响应面进行响应面拟合。Kriging响应面是一种同时从局部和全局角度考虑影响因素的多维插值技术,所有的试验设计点都坐落在响应面上,对于非线性的工程优化问题具有较高的适应性[15,18]。KAYMAZ[19]和黄章俊等[20]的研究说明了Kriging响应面具备较好的非线性效果,证明了Kriging方法应用于优化设计的可行性和优越性。设计变量对目标参数的Kriging响应面如图5所示,在设计变量范围内,链环最大等效应力存在极小值,即可以找到一个最优方案使得等效接触应力最小。
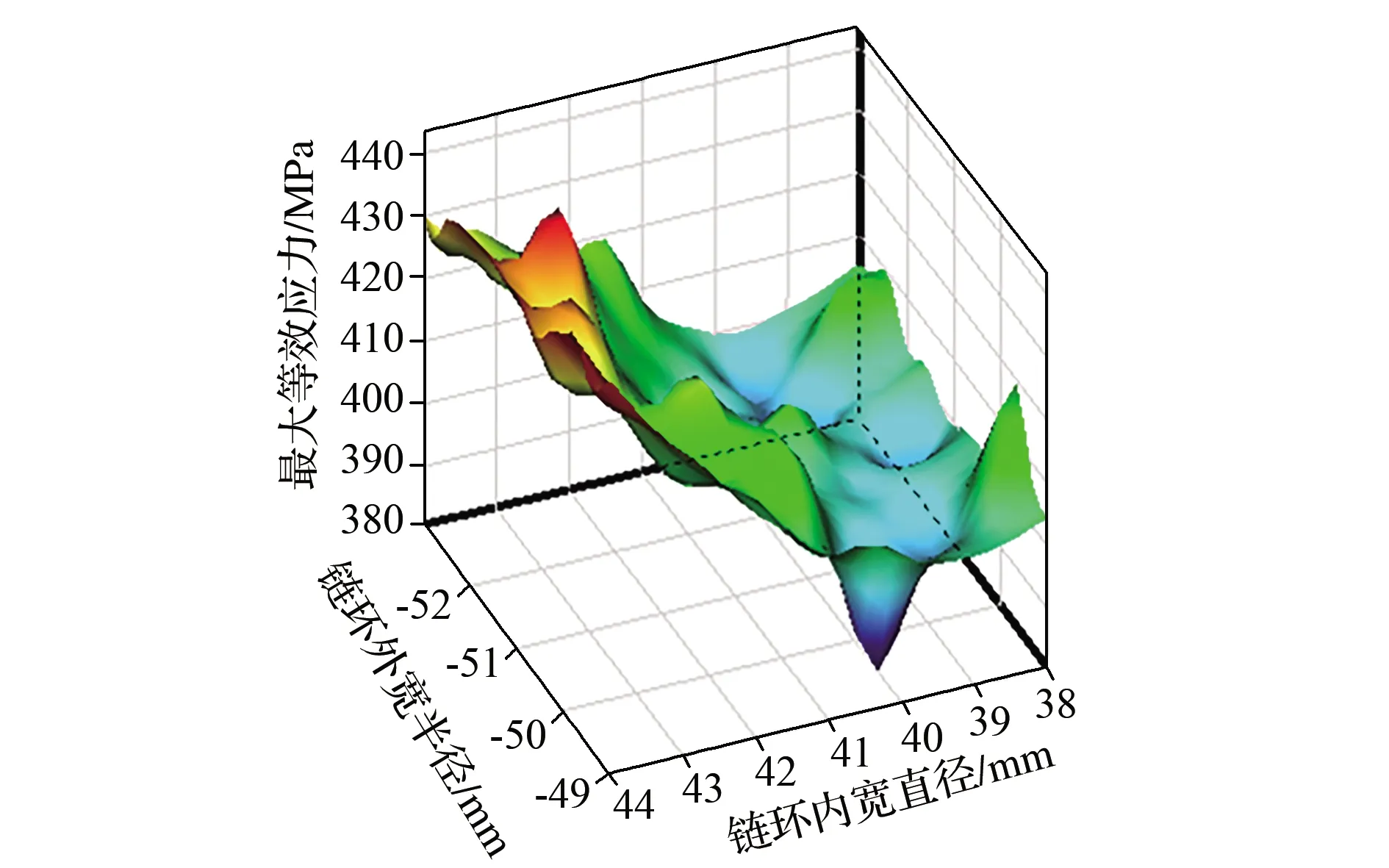
图5 设计变量对最大等效应力的Kriging响应面
敏感度是输出响应值对设计输入变量的偏导数,用于表征设计输入参数变化对于目标输出参数的影响程度。从Workbench中导出的设计变量对输出参数的敏感度如图6所示。
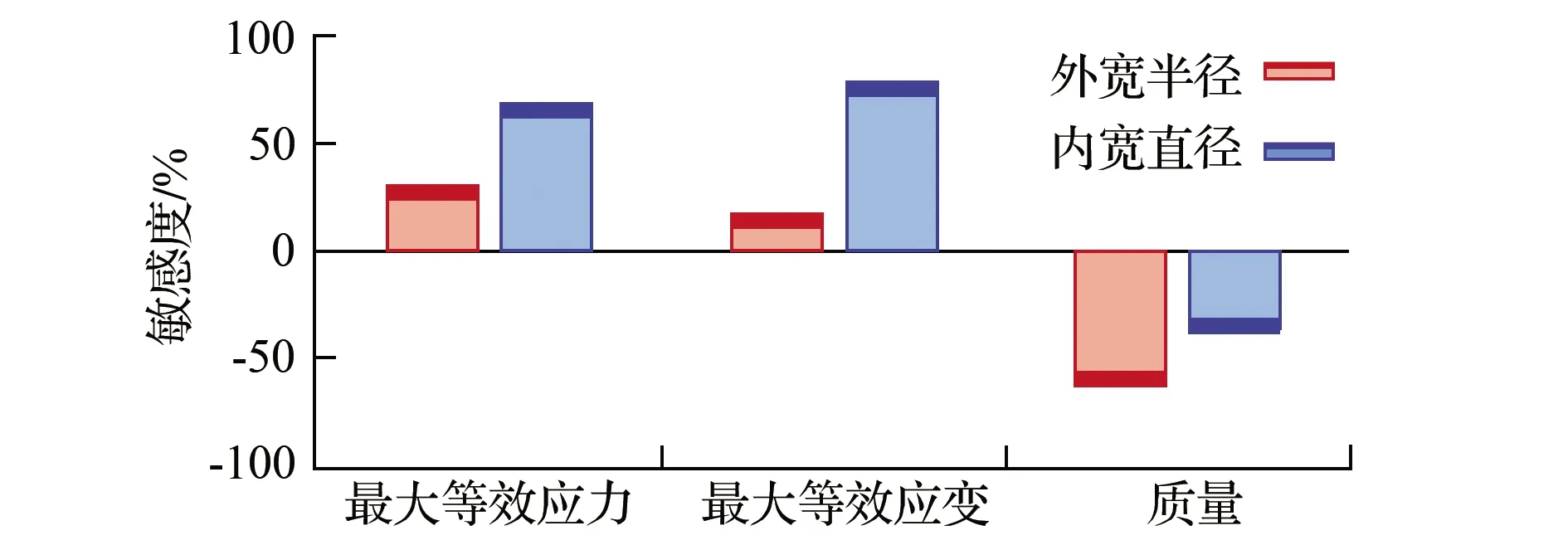
图6 设计参数对目标参数的敏感度
由图6可知,对于链环最大等效应力和最大等效应变而言,内宽直径的相关性程度(69.195%和79.350%)比外宽半径(30.194%和17.282%)更大;而对于链环质量,链环外宽半径(-63.076%)比内宽直径(-37.876%)具有更大的影响程度。
3.2.3 优化方案求解及验证
响应面生成以后,本文选用多目标遗传算法[21]进行寻优求解。设置初始样本点数为1000,每次迭代样本点数为100,候选设计点数为5,设置目标函数为最大等效应力和最大等效应变最小,迭代求解后得到5个候选设计方案及其理论求解结果。然后将各候选设计点代入静力学分析模块进行验证,其理论值与验证结果见表5。所有候选方案中理论值与验证值间的最大相对误差仅为1.00%,表明迭代结果具有较高的可信度。

表5 优化方案候选表
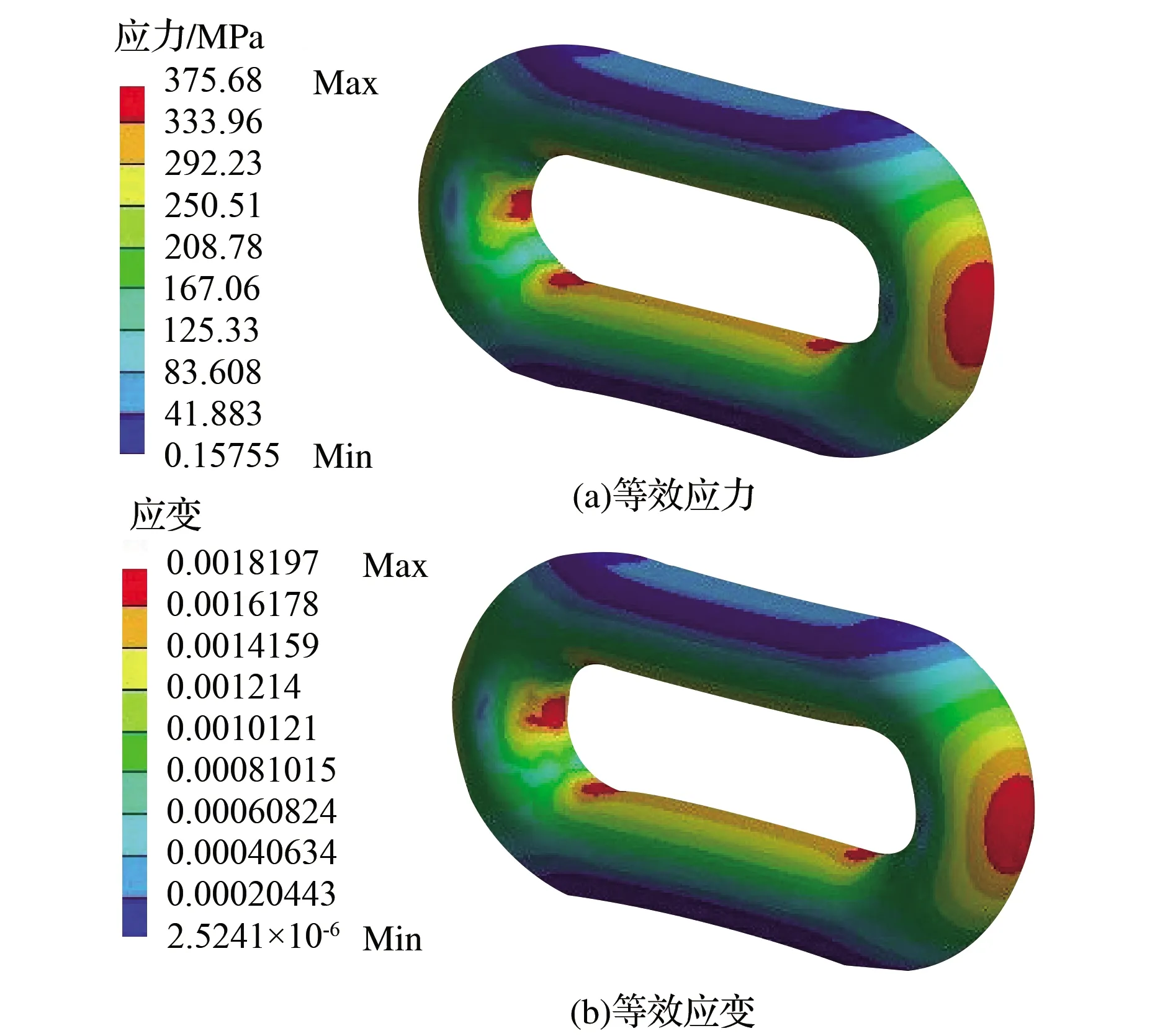
图7 响应面优化后链环2的等效应力应变
由表5可知,在相同的载荷及约束作用下,方案4中的链环2的最大等效应力、最大等效应变和质量最小,说明方案4(链环外宽半径为-49.598mm、内宽直径为40.02mm)是最优的设计方案。方案4的链环2的等效应力和等效应变分布如图7所示,与优化前的对比情况见表6。与拓扑优化相比,响应面优化后的链环虽然在质量上增长了0.37%,但在最大等效应力和最大等效应变分别降低了6.61%和5.70%。与未优化的标准圆环链相比,经过响应面优化的链环的质量由2.841kg降为2.743kg,降低了3.45%;在接触效应方面虽然依旧存在应力集中现象,但链环直圆柱和圆环部位间过渡区间的应力和应变分布较优化前更加均匀,其最大等效应力已由400.04 MPa降低到375.68 MPa,减小了6.09%,最大等效应变由0.00195降低到0.00182,减小了6.67%。
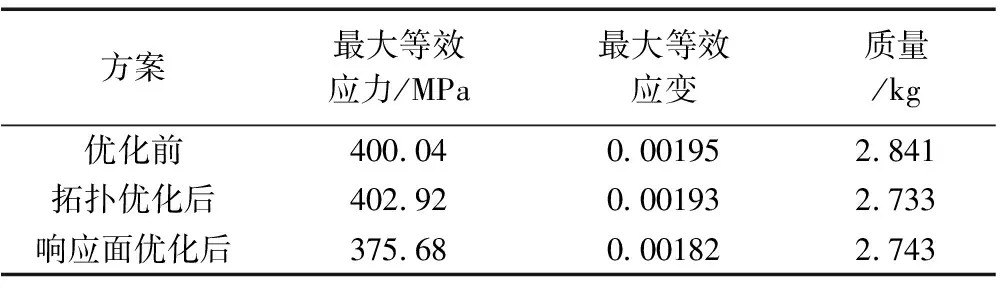
表6 圆环链优化前后结果对比
4 结 论
1)圆环链在拉力载荷作用下,链环的等效应力和等效应变呈现明显的对称分布,在链环与链环间的接触部位以及链环直圆柱和圆环过渡弯曲部位存在着明显的应力和应变集中现象,最大等效应力和等效应变分别为400.04MPa和0.00195。
2)经过拓扑优化,对链环直圆柱部分的外侧进行削平处理,链环自重降低了3.80%,实现了链环轻量化的目的,但最大等效应力增大了0.72%。
3)在拓扑优化的基础上对链环进行响应面优化设计,其中链环内宽直径对链环最大等效应力和最大等效应变的相关程度比链环外宽半径更大,而在链环质量方面链环外宽半径比内宽直径具有更显著的影响。
4)响应面优化后,链环自重减小了3.45%,链环最大等效应力和最大等效应变各自降低了6.08%和6.67%,改善了接触状态。
