磁休克治疗对重度抑郁症患者脑功能网络的影响*

田树香 徐桂芝** 王龙龙 刘向向 FITZGERALD B Paul

（1）河北工业大学电气工程学院，省部共建电工装备可靠性与智能化国家重点实验室，天津 310130；2）河北工业大学电气工程学院，河北省生物电磁与神经工程重点实验室，天津 310130；3）Epworth Centre for Innovation in Mental Health,Epworth Healthcare and Monash Alfred Psychiatry Research Centre,Monash University,Melbourne 3004,Australia)

随着生活节奏日益加快，竞争压力不断增大，越来越多的人罹患抑郁症。根据2021年权威数据显示，全球大约有2.8 亿人患有抑郁症，仅中国就有高达5 400 万抑郁症患者［1］。重度抑郁症（major depressive disorder，MDD）是一种多相性障碍疾病，包括情感、认知、行为和躯体调节功能等多方面，严重威胁人们工作和生活［2］。电休克治疗（electroconvulsive therapy，ECT）是目前治疗抗药性抑郁症最有效的疗法，但对认知有一定的副作用［3‑4］；磁休克治疗（magnetic seizure therapy，MST）是通过高强度和高频率的重复经颅磁刺激（transcranial magnetic stimulation，rTMS）诱导癫痫信号发作的治疗方法，在MDD的治疗中具有与ECT相似的疗效［5‑8］，然而目前对MST的抗抑郁机制研究仍不完善。

目前，无论是在临床诊疗中还是在药物临床试验中，抑郁症严重程度和治疗后疗效的评估尚缺乏可靠的客观指标。使用经过验证且具有良好信效度的量表是目前通行的评估方法，主要包括汉密尔顿抑郁 量 表（Hamilton depression scale，HDRS）［9］和蒙哥马利‑艾斯伯格抑郁量表（Montgomery‑Asperger depression scale，MADRS）［10］等。近年的研究发现MST 治疗MDD 的有效率在20%～70%［11‑13］。

大脑是一个非常复杂的系统，由多个神经元、神经元集群或者多个脑区相互连接组成庞杂的结构网络，高级的大脑功能除了局部活动参与外，还依赖不同脑区之间的协同作用［14］。功能连接是指空间上分离的神经单元的神经活动在时间上的关联性或统计依赖关系［15］，通过全脑功能网络连接分析，可以了解大脑网络组织和连接模式的异常。图论的方法定义了基于节点及其对应边缘的大脑网络［16］，提供了一系列量化复杂网络组织的指标，可用于分析来自神经影像数据（包括脑电图（EEG）信号）的网络拓扑结构［6，17］。研究不同时空尺度上脑网络拓扑结构、动力学属性等内容，可以更好地探究神经精神疾病的病理［18］。

功能性神经影像学研究的结果表明，抑郁症状与静息状态下大脑网络的连通性异常有关［19‑21］，抑郁症患者中与执行功能和认知控制有关的前额‑顶叶脑区存在一定程度的低连通性［12］。近年来多项研究发现，MDD患者在MST后网络连接和拓扑结构发生变化，并且在治疗有效组和无效组的对比分析中也体现出巨大差异［17，22‑23］。Hill 等［17］研究结果表明，MDD 患者在MST 后伴随θ 频段和β 频段连通性的改变。Bailey 等［24］对rTMS 治疗前后MDD患者的静息态EEG进行研究，发现治疗有效组表现出更高的θ 网络连通性。Gold 等［25］比较了TMS 后治疗有效组和无效组之间的EEG 微观状态特征，发现临床治疗反应与微状态MS‑2 特征的增加以及MS‑3 特征的降低有关，且治疗无效组在任何微观状态下都没有显著变化。Deng 等［26］对MST 后记录的静息态脑电信号，使用去偏加权相位滞后指数评估功能连通性，发现MDD 患者β 频段的功能连通性下降，并且与治疗无效组相比，治疗有效组的Delta频段网络连接密度也有显著增加；同时对几种基于图论的指标（包括节点度、聚类系数、网络连接密度和特征路径长度等）进行连通性分析，发现MST 有可能调节大脑中的隔离（聚类系数）和整合（特征路径长度）。

以上研究表明，磁休克治疗可能对MDD 患者的静息态脑功能具有一定的调控作用。较低的治疗有效率限制了分析结果的准确性，多数研究集中在对所有MDD患者进行整体评估，较少根据疗效进行二次分析。本文利用17 项汉密尔顿抑郁量表（HDRS‑17）评分作为主要疗效指标评估工具，并根据抑郁症状的改善程度，进一步区分治疗有效组和治疗无效组，在全部MDD患者组、治疗有效组和治疗无效组中展开对比分析；然后利用静息状态脑电信号，构建基于皮尔逊相关的脑功能网络，并从复杂网络的角度分析网络拓扑结构的变化，以探究MST 对MDD 患者的静息态脑功能改变的作用机理。

1 信号采集与数据预处理

1.1 实验对象

本文依托河北工业大学和莫纳什大学科研平台展开相关研究，实验数据采集对象为澳大利亚Alfred 医院的18 名MDD 患者（男10 名，女8 名），平均年龄为（44.76±14.93）岁。所有MDD 患者在实验前签署知情同意书，且均符合美国精神障碍诊断与统计手册第4 版（DSM‑IV）重度抑郁诊断标准，HDRS‑17 评分＞18。本研究获得了澳大利亚Alfred健康人类研究伦理委员会和莫纳什大学人类研究伦理委员会批准，并符合世界医学协会的伦理守则（赫尔辛基宣言），该试验已在澳大利亚‑新西兰临床试验注册处注册 （ANZCTR：ANZCTRN12611000054910）。

1.2 实验设备及方案

脑电记录设备：EEG 数据采集设备为美国NeuroScan 公司生产的脑电采集以及同步分析系统，记录系统由64 导Quick‑cap 电极帽、SynAmps第二代放大器和记录分析处理计算机组成，其电极安放标准遵循国际通用标准10‑10 系统放置方法。接地电极为头顶GND，参考电极为REF。导联的采样率为10 kHz。所有电极的阻抗均保持在5 kΩ以下。

脑电数据预处理：使用Matlab （R2020a）EEGLAB 工具箱进行预处理。去除眼电和双侧乳突等电极，保留60个导联，参考电极选择头顶Cz。EEG数据首先被降频到1 kHz；使用零相四阶巴特沃斯滤波器进行滤波（0.2～45 Hz）；使用算法检测并去除不良通道，并对去除的通道进行插值；使用独立成分分析（ICA算法）来消除伪影；全脑平均作重参考。

磁休克治疗设备：本研究使用具有双线圈的刺激仪（MagPro MST；MagVenture，Denmark）在全身麻醉状态下进行MST。根据国际10‑10 系统，将双线圈对称地放置在Fz 电极，确保两个线圈的中心覆盖F3 和F4。使用异丙酚（Propofol，又名“丙泊酚”）作为麻醉剂，氯化琥珀胆碱用作神经肌肉阻滞剂。所有患者最初都进行阈值剂量滴定，以确定诱发癫痫发作所需的刺激强度［13，17］。以100 Hz 的脉冲波进行刺激，滴定将从2 s 的刺激开始，以2 s 的增量增加，直到确定癫痫发作。然后以患者发作阈值+4 s时长的强度用于治疗（如果发作阈值为2 s，则进行6 s 的治疗）。每周在周一、周三和周五进行3 次刺激治疗，治疗时长为3～4周，直到满足抑郁症状的缓解标准（两次连续评分，HDRS‑17 得分≤10 且抑郁症状降低≥50%）［27］，或总共进行12次治疗。

1.3 实验方案设计

所有MDD患者的静息态EEG实验数据采集工作均在安静、适宜的环境，采集过程中，要求MDD 患者安静、放松但要保持头脑清醒。实验方案具体流程为：在MST 过程开始之前的48 h 内先进行一次静息态EEG 信号记录（5 min）和HDRS‑17 量表评估（pre‑MST）；然后进行3～4 周的MST治疗；最后，在MST 疗程结束后48 h 内再进行一次静息态EEG信号记录（5 min）和HDRS‑17量表评估（post‑ MST）。实验方案设计流程如图1所示。

Fig.1 The process of experimental program

脑电数据分析是通过记录MDD患者在MST作用前后的静息态EEG 信号，并对EEG 信号进行分析和处理，提取神经生理学特征，并与抑郁量表评分相结合，从而探究MST对MDD患者大脑的调控作用影响。

1.4 统计学分析

本实验所得数据采用t 检验进行统计学分析，以P值大小为参考对不同组间数据差异是否有统计学意义进行判断，认为当P＜0.05时数据具有显著性差异并记为“#”，P＜0.01 时记为“##”，P＜0.001 时记为“###”。其中，实验前后对照组数据采用配对样本t检验，其他组间数据采用不假定等方差的独立样本t检验。

2 脑电数据处理

2.1 脑功能网络构建

本研究选取皮尔逊相关［28‑29］网络连接模型，基于皮尔逊相关系数（Pearson correlation coefficient）rij构建相关系数矩阵。任意两个通道的EEG信号序列用xi和xj随机变量表示，在时域上的皮尔逊相关系数rij定义如式（1）所示。皮尔逊相关系数rij的大小反映了不同通道之间EEG 信号相关程度的高低，取值在0～1 之间，数值越接近1，表示相关程度越高；数值越接近0，表示相关程度越低。

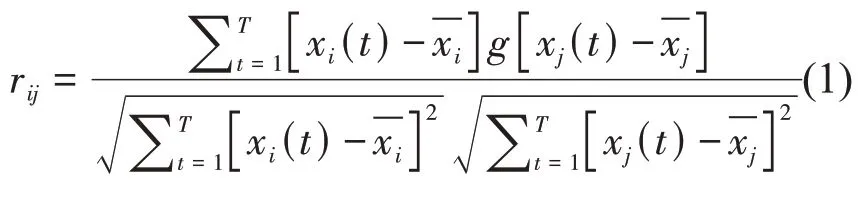
其中：t 为时间，T 为时间序列总长度；xi、xj分别表示导联i 和导联j 的时间序列；表示时间序列的均值。

计算每位MDD 患者在MST 作用前后60 个导联之间的正相关系数，并对所有MDD患者的皮尔逊相关系数矩阵求均值，得到平均皮尔逊相关系数关联矩阵。阈值的选取同时满足每个MDD患者脑功能网络和平均脑功能网络没有孤立节点或孤立部分，且具有小世界属性。本研究中阈值选取为（0.53～0.8）。每个通道的EEG信号与其自身的皮尔逊相关系数为0，也就是皮尔逊相关系数矩阵的对角元素为0，以避免网络中有自连接的边存在。根据事先设定好的阈值将平均关联矩阵转换成二值矩阵，即当rij大于该阈值时对应二值矩阵的对应元素为1，否则为0，由此得到一个60×60 的时间序列相关矩阵。

最后构建平均脑功能网络，当皮尔逊相关系数大于阈值时，两个导联之间存在连接，否则没有连接，可以得到MDD患者在MST作用前后的平均脑功能网络。在构建脑功能网络的基础上，求取网络的平均节点度、平均聚类系数、平均最短特征路径长度、平均全局效率和小世界属性等5 个特征参数，通过对比分析网络参数的不同，来定量分析评价脑功能网络在治疗前后的差异。

2.2 复杂网络分析

2.2.1 节点度

度是复杂网络节点的属性中最简单但也是最重要的性质。一个节点i的度表示与它相连的节点数目，一个节点的度越大就意味着和它相连接的节点越多，这个节点在网络中的影响也越大［30］。网络的平均节点度以符号K 表示，其计算如式（2）所示：

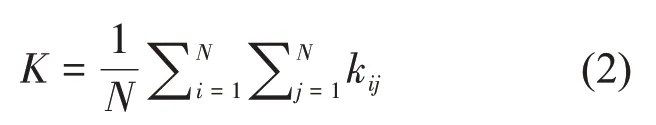
其中，N表示网络的总节点数，kij表示在二值网络中第i个节点与第j个节点之间的连接数。

2.2.2 聚类系数

聚类系数常用来描述网络的集成度或节点的密集程度，节点i的聚类系数表示它的所有邻近节点之间当前存在的边数与所有邻近节点之间能够存在的最多边数之比。聚类系数越大，表示网络中该节点局部连接越紧密［30］。所有节点的平均聚类系数C定义为网络的聚类系数。网络的平均聚类系数定义如式（3）所示：

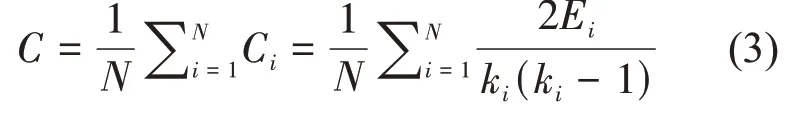
其中，N表示网络的总节点数，ki为节点i的度，Ei为节点i的相邻节点间存在的边数，Ci为节点i的聚类系数（若ki＜2，则Ei＝0）。

2.2.3 特征路径长度

特征路径长度是衡量网络信息传输快慢的重要参数。在脑功能网络中，连接节点i 和j 所经过的最少边数就是这两个节点的最短路径长度。网络中所有节点的最短路径长度求平均就是特征路径长度，最短路径长度和全局效率度量了网络的全局传输能力。特征路径长度越短，网路的连通性越好，表明网络信息传输速度越快。所有节点的平均特征路径长度L计算如式（4）所示：

其中，N表示网络的总节点数，dij为节点i和节点j之间的最短路长度。

2.2.4 全局效率

全局效率是衡量网络中信息传输效率的重要参数。网络中所有节点的最短路径长度倒数的平均值就是网络的全局效率，全局效率越高说明信息传输效率越高。所有节点的平均特征路径长度Eglob计算如式（5）所示：

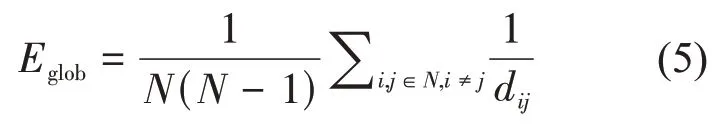
其中，N表示网络的总节点数，dij为节点i和节点j之间的最短路径长度。

2.2.5 小世界属性

1998年Watts 等［31］提出了具有较大聚类系数和较短特征路径长度的网络为小世界网络，用参数σ 来衡量。当σ 值大于1 时，说明网络具有小世界属性，且σ值越大，小世界属性越强，网络信息在全局和局部的传输效率越高。小世界属性σ的计算如式（6）所示：

其中，C和L表示所构建网络的平均聚类系数和平均最短特征路径长度，Cr和Lr表示随机网络的平均聚类系数和特征路径长度，随机网络的节点数目和连接边数与所构建网络相同。

2.2.6 网络连接密度

网络连接密度可以表征网络通道节点之间连接数目的多少，用CD表示，定义如式（7）所示：

其中，N表示通道数量，K表示矩阵网络中所有非零元素的数量。

3 结 果

3.1 抑郁量表评估

为研究MDD 患者在MST 作用前后的疗效改变，本文分别对所有MDD患者在MST作用前后的HDRS‑17 量表分值进行均值化。治疗有效（response，简称res），也称为“有反应”，是指治疗后抑郁症状明显减轻，本文以HDRS‑17 量表评分变化率≥50%来定义，反之为治疗无效（non‑response，简称non），也称为“无反应”［27］。

全部MDD患者在MST治疗前后的平均HDRS‑17 量 表评 分 为（27.1±4.6），在MST 后的 平均HDRS‑17 量表评分为（22.2±5.6），评分变化率为18.1%，说明MST 改善了MDD 患者的抑郁症状。其中4 人的HDRS‑17 评分变化率≥50%，达到治疗有效标准，为res组；另外14人的HDRS‑17评分在MST 后有所降低，但没有达到治疗有效标准，为non组；全部MDD患者组为all组。

3.2 脑功能网络连通性分析

本文对所有MDD 患者在MST 作用前后各5 min 时间段内的静息态EEG 数据进行相关性分析。利用皮尔逊相关系数公式，计算可得60×60的关联矩阵，并将所有MDD 患者的关联矩阵均值化，可得到MST 作用前（图2a）后（图2b）的皮尔逊相关系数矩阵（图2）。矩阵图中颜色越接近蓝色，表示两个通道的皮尔逊相关系数越小；颜色越接近红色，表示两个通道的相关系数越大。颜色棒表示皮尔逊相关系数r值的大小，颜色越接近红色表示对应通道间的相关系数越大，连接性越强；反之，颜色越接近蓝色表示对应通道间的相关系数越小，连接性越弱。

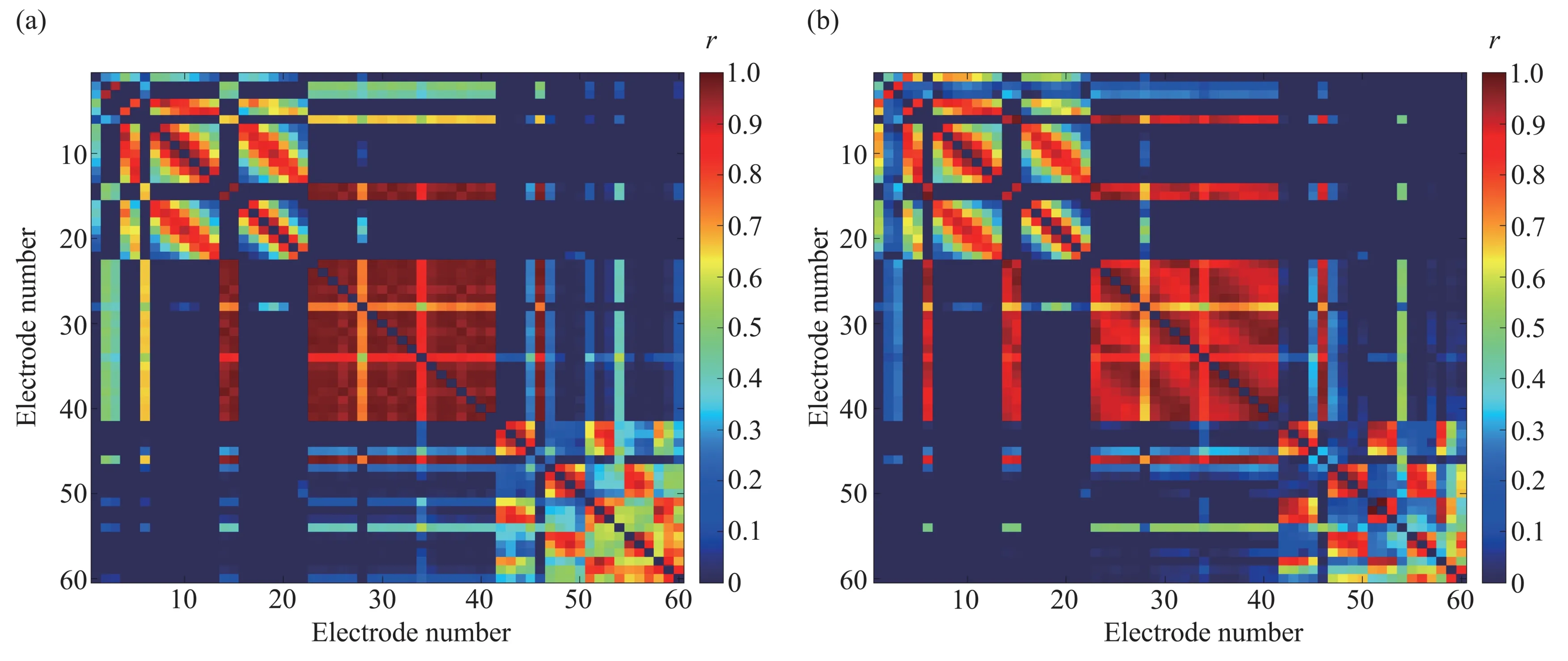
Fig.2 The Pearson correlation coefficient matrix pre-and post-MST treatment(a)The matrix pre‑MST treatment.(b)The matrix post‑MST treatment.

根据选取的阈值（0.53～0.8），在皮尔逊相关系数矩阵基础上，可以得到MST 作用前（图3a）后（图3b）所有MDD 患者的平均二值矩阵（图3）。在皮尔逊相关二值矩阵图中只包含有0和1两种元素，其中蓝色表示二值矩阵中元素为0，即两个通道之间没有相关性；红色表示二值矩阵中元素为1，即两个通道之间有相关性。

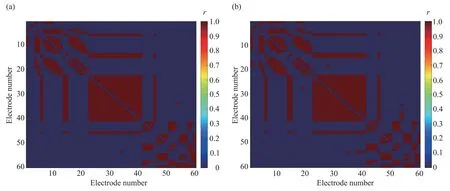
Fig.3 The Pearson correlation binary matrix pre-and post-MST treatment(a)The matrix pre‑MST treatment.(b)The matrix post‑MST treatment.

皮尔逊相关系数值反映了不同电极通道之间神经信号时域相关性的强度大小。当二值矩阵中的元素为1时，将该元素对应两个通道的电极位置相连接，把相关系数矩阵中对应位置的元素作为权重，从而得到网络的一条连接边；当皮尔逊相关二值矩阵中的元素为0时，则该元素对应的两个通道的电极之间无连接边。由此可得MST 作用前（图4a）后（图4b）所有MDD患者的加权脑功能网络连接图（图4）。图4c为MST作用前后连接密度变化对比图，图4d 为MST 作用前后连接强度变化对比图。MST 后左侧前额网络连接减少，左侧中额及颞叶上部网络连接增加（图4a，b）。全脑功能网络连接密度在MST后明显增加（图4c），脑功能网络连接变密集。经配对样本t检验，MST作用前后的连接密度存在统计学差异（t=-1.521，df=17，P=0.012）。全脑功能网络连接连接强度在MST 后明显增加（图4d），脑功能网络连接增强。经配对样本t检验，MST作用前后的连接强度存在统计学差异（t=-1.059，df=17，P=0.048）。结果表明，MST改变了MDD患者脑功能网络连接，在全脑平均水平上，功能连通性得到改善。

3.3 脑功能网络参数

为研究MST 对MDD 患者网络拓扑结构的改变，本文在构建的皮尔逊相关网络的基础上，对比分析MDD患者在MST前、后两种状态下脑功能网络的平均度、平均聚类系数、平均路径长度、平均全局效率和小世界属性等5 个特征参数，再利用t检验进行统计学分析，来定量描述分析脑功能网络特征。

平均节点度可表征网络的连接强弱，平均度值越大，表明网络的连接越强。平均聚类系数度量网络的集团化程度和局部信息的传输能力，也在一定程度上反映了网络防御随机攻击的能力。平均聚类系数越大，表明网络的集团化程度越高，局部信息传递能力越强。MST 作用前后脑功能网络的平均节点度和聚类系数对比结果如图5所示。图5a为各组平均节点度在MST 作用前后变化对比图，图5b为平均最短特征路径长度在MST 作用前后变化对比图。

由图5a可以看出，全部MDD患者组的平均节点度在MST 作用前后无显著差异（配对样本t 检验，P＞0.05）。治疗有效组的平均节点度在MST后明显增加，经配对样本t检验，治疗有效组MST作用前后的平均节点度存在统计学差异（t=-2.402，df=3.197，P=0.007）。治疗无效组的平均节点度在MST 后无显著变化（配对样本t 检验，P＞0.05）。结果表明，治疗有效组的MDD患者的平均节点度在MST 后显著增加，表现为网络连接增强；治疗无效组的平均节点度在MST后变化不显著。

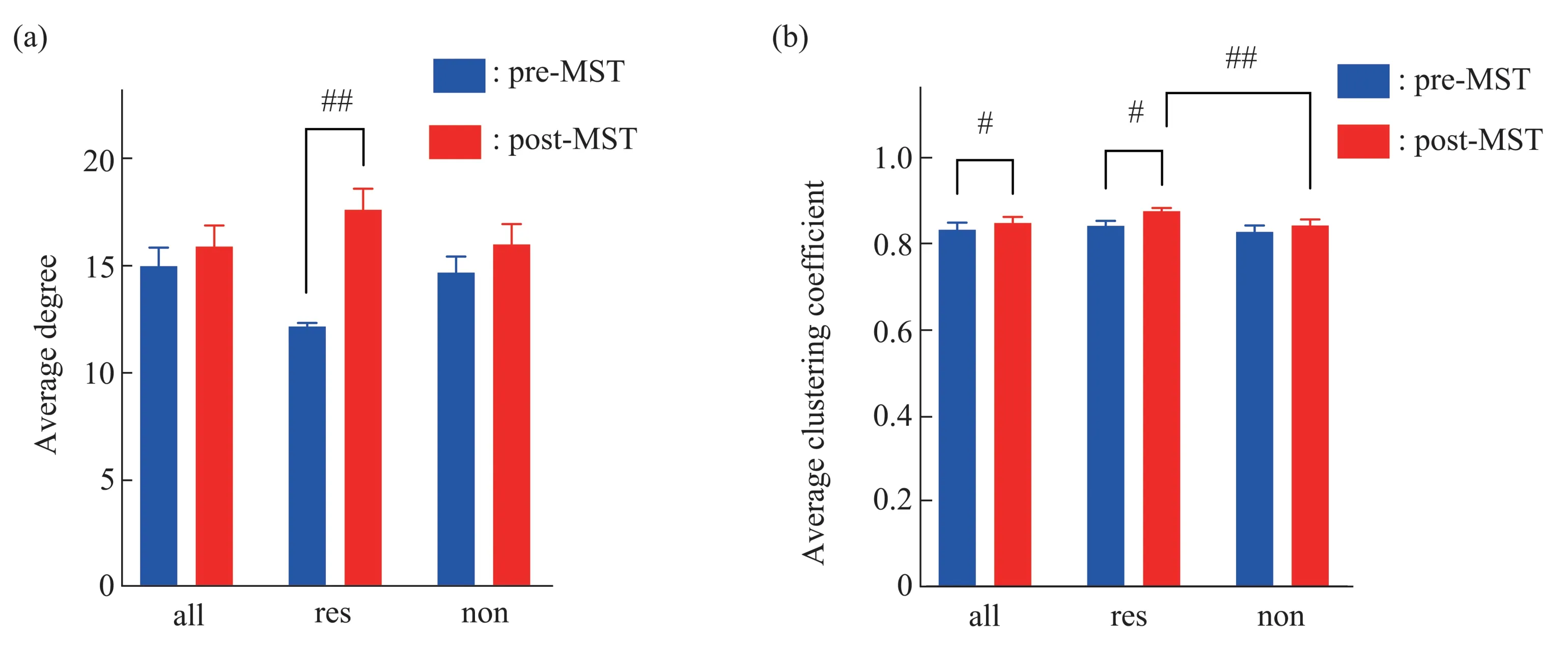
Fig.5 The comparison of average degree and average clustering coefficient in brain network pre-and post-MST treatment(a)The comparison chart of the average node degree of each group pre‑and post‑MST.(b)The comparison chart of the average clustering coefficient of each group pre‑ and post‑MST. “all” is the group of all MDD patients, “res” is responders, “non” is non‑responders. #P＜0.05, ##P＜0.01, ##P＜0.01.

由图5b可以看出，全部MDD患者组和治疗有效组的平均聚类系数均在MST 后明显增加，各组在MST 作用前后的平均聚类系数均存在统计学差异（res 组：t=-0.997，df=5.325，P=0.026；all 组：t=-0.314，df=4.113，P=0.042）。治疗有效组和治疗无效组的平均聚类系数在MST 前无显著差异。治疗有效组的平均聚类系数在MST 后大于治疗无效组，经独立样本t检验，两组的平均全局效率存在统计学差异（t=1.635，df=7.860，P=0.009）。结果表明，MST增大了MDD患者脑功能网络的聚类系数，网络的集团化程度和局部信息传递能力显著增强，并且治疗有效组网络的改善优于治疗无效组。

平均最短路径长度和全局效率均反映网络的信息传递效率。平均最短路径长度越小，表明网络的信息传递效率越高，相反，全局效率越大，网络的信息传递效率越高。MST 作用前后脑功能网络的平均最短路径长度和全局效率对比结果如图6 所示。图6a 为各组平均最短路径长度在MST 作用前后变化对比图，图6b 为各组平均全局效率在MST作用前后变化对比图。

Fig.6 The comparison of average path length and global efficiency in brain network pre-and post-MST treatment(a)The comparison chart of the average path length of each group pre‑ and post‑MST. (b)The comparison chart of the average global efficiency of each group pre‑and post‑MST(#P＜0.05).“all”is the group of all MDD patients,“res”is responders,“non”is non‑responders.

由图6a 可以看出，治疗有效组的平均最短路径长度在MST 后明显降低，治疗有效组的平均最短路径长度大于治疗无效组，经配对样本t 检验，治疗有效组MST 作用前后的小世界属性存在统计学差异（t=2.581，df=5.800，P=0.043）。而在治疗无效组和全部MDD患者组的平均最短路径长度在MST 作用前后无显著变化（配对样本t 检验，P＞0.05）。结果表明，MST 仅仅降低了治疗有效组MDD 患者的平均最短路径长度，治疗有效组脑功能网络的信息传递效率得到提升，MST 改善了MDD患者网络的信息传递效率。

由图6b可以看出，全部MDD患者组、治疗有效组和治疗无效组的平均全局效率均在MST 后明显增加，经配对样本t检验，各组在MST作用前后的全局效率均存在统计学差异（res 组：t=-0.848，df=4.316，P=0.041；non 组：t=-0.221，df=3.964，P=0.035；all 组：t=-0.558，df=3.624，P=0.039）。治疗有效组和治疗无效组的平均全局效率在MST前无显著差异。治疗有效组的平均全局效率在MST后大于治疗无效组，经独立样本t检验，两组的平均全局效率存在统计学差异（t=0.848，df=5.990，P=0.029）。结果表明，MST 增大了抑郁症患者的平均全局效率，网络的信息传递效率显著增强；MST 作用后，治疗有效组信息传递效率的改善优于治疗无效组。

小世界属性量化了复杂网络特性，是衡量所构建的网络是否为小世界网络的基准。小世界属性大于1，表明网络具有小世界网络特征，且值越大，网络的小世界特征越强。进一步对网络的小世界属性进行对比分析（图7）可以看出，全部MDD 患者组、治疗有效组和治疗无效组的平均小世界属性在MST 后均大于MST 前。经配对样本t 检验，治疗有效组的小世界属性在MST 作用前后存在统计学差异（t=-2.482，df=3.783，P=0.007）。治疗无效组和全部MDD组的平均小世界属性在MST作用前后无显著差异。治疗有效组的平均小世界属性在MST后大于治疗无效组，经独立样本t检验，两组的小世界属性存在统计学差异（t=3.677，df=13.233，P=0.033）。结果表明，MST 增大了MDD患者脑功能网络的小世界属性；且MST 作用后，治疗有效组的小世界属性显著大于治疗无效组。

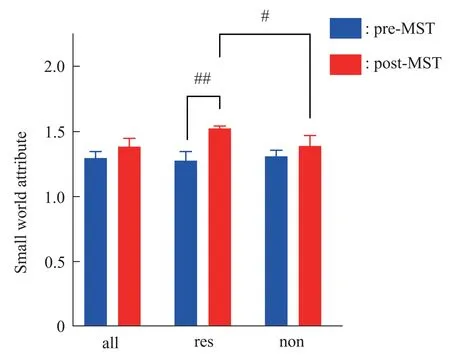
Fig.7 The comparison of small world attribute of each group pre-and post-MST treatment“all” is the group of all MDD patients, “res” is responders, “non” is non‑responders.#P＜0.05,##P＜0.01.

4 讨 论

本文基于皮尔逊相关算法，构建了MST 作用前后的EEG 脑功能网络，并引入平均节点度、最短路径长度、聚类系数、全局效率、小世界属性、网络连接密度以及连接强度等特征参数，通过对比MST 作用前后的网络拓扑属性差异，讨论分析了MST对MDD患者脑功能网络的作用影响。

汉密尔顿抑郁量表评估结果表明，所有MDD患者在MST后，平均HDRS‑17评分显著低于MST前，说明抑郁症状有了显著改善。根据抑郁症的疗效评估标准进一步区分治疗有效组和治疗无效组。在MST 前，治疗有效组和治疗无效组的HDRS‑17评分无显著差异；在MST 后，治疗有效组和治疗无效组的HDRS‑17 评分也没有显著差异，但是治疗有效组抑郁症状的改善优于治疗无效组。

脑功能网络是将大脑看作复杂的统一整体，研究不同时空尺度上脑网络拓扑结构、动力学属性等内容，为理解脑的信息加工过程及脑的高级功能提供了全新的视角［16］。本文利用皮尔逊相关方法构建了MST 作用前后的EEG 脑功能网络。网络连接分析结果表明，MST 改变了大脑不同区域的脑功能连通性，全脑平均水平上的脑功能连接密度显著增加，连接强度显著增加，脑功能网络变密集，复杂程度变大。复杂网络分析结果表明，MDD 患者脑功能网络的平均度、平均聚类系数、平均全局效率值和小世界等属性在MST 后显著增加，平均最短特征路径长度显著减小；且相比治疗无效组，治疗有效组脑功能网络的平均度值、平均聚类系数、平均全局效率和小世界属性增加更多；同时脑功能网络的平均路径长度值减小更多。

以往的研究发现，MST在MDD的治疗中发挥着重要作用，并对患者的脑功能网络具有一定的调制作用［12‑13］。Hill 等［17］对MST 作用前后的功能连通性、网络拓扑等进行研究，发现θ频段的功能子网连通性增大；聚类系数在MST 后显著增加，而特征路径长度显著下降。功能性神经影像学研究的结果表明，额叶顶区域内的低连通性程度与MDD的执行功能和认知控制有关［32］。Atluri 等［33］通过脑电图微观状态分析发现，MST 后治疗有显著变化的区域通常位于额叶、顶叶和枕叶脑等，治疗有效组微观状态的持续时间显著增加、频率显著降低。本文研究结果基本与前人研究结论［6，17，20］一致，表明MST 作用会改变MDD 患者的脑网络结构，使不同的神经元或脑区之间的交互增加，网络连通性增强，信息交流传递能力得到优化，从而表现为抑郁症状的改善，即HDRS‑17 评分的降低。同时，治疗有效组MDD患者的脑功能网络特征参数变化量更大，推测脑功能网络特征参数的变化与HDRS‑17评分的改变相关。

脑电特征参数也被用来预测MST 的抗抑郁治疗反应。Hoy 等［11］研究表明，MDD 患者在接受100 Hz 的MST 作用后，治疗有效组和无效组之间的大脑激活区域存在差异。MST 治疗前α2 频段的脑功能连通性对MST 治疗的疗效有预测价值［34］；脑电微状态中状态C和D持续时间的相对变化被证明是MST疗效的强有力预测因素［33］。Bailey等［24］研究表明，从治疗前到治疗1周期间，治疗有效组在额顶叶和顶枕区域表现出更高的θ网络连通性变化，显示出预测rTMS治疗重度抑郁症的潜力；使用交叉验证的机器学习分类法，结合所有EEG 和情绪测量，可以将治疗有效组和无效组区分开来，平均灵敏度为0.84（P=0.001），特异性为0.89。本文结合HDRS‑17 量表评分和脑功能网络特征进行研究，发现相比于治疗无效组，治疗有效组具有更高的HDRS‑17 评分变化率、更显著的网络连通性以及网络拓扑属性变化。基于EEG 的网络特征显示出一定的预测潜力，因此MDD的MST作用客观电生理指标分析和疗效预测也将是今后研究的重点。通过简单的EEG 测量，进行疗效预测，可以大大减少患者和临床负担。

5 结 论

为了研究MST 治疗对MDD 脑功能网络的影响，本文对MST作用前后MDD患者的静息态脑电信号进行采集，根据治疗前后的HDRS‑17 评分变化，区分治疗有效组和治疗无效组；基于皮尔逊相关方法构建脑功能网络，并从复杂网络的角度，对比分析MST治疗前后的网络特征参数。结果表明，MST改变了MDD患者脑功能网络连通性和网络拓扑结构，且对治疗有效的MDD患者网络改变更为显著。本文研究结果有助于对磁休克治疗抗抑郁机制的理解，同时对MDD的临床治疗和评估具有重要意义。