改进最小二乘法在永磁同步电机参数辨识中的应用
2022-07-21李祥功朱立军
李祥功,朱立军,2,陈 猛
(1.沈阳化工大学 计算机科学与技术学院,辽宁 沈阳 110142;2.沈阳化工大学 辽宁省化工过程工业智能化技术重点实验室,辽宁 沈阳 110142;3.中国科学院大学,北京 100049;4.中国科学院大学沈阳计算技术研究所,辽宁 沈阳 110142)
0 引 言
永磁同步电机(PMSM)因其结构简单、功率密度大、效率高等优点,近年来一直被广泛应用于工业领域,特别是一些需要精密控制的场合,比如数控机床、航空航天、电动汽车等。永磁同步电机通常采用基于矢量控制的闭环控制方法,在这种控制方法中准确了解电机的参数对电机的高性能所起的作用至关重要。然而永磁同步电机在运行过程中,其参数可能会随着温度、机器老化和环境条件而变化,从而导致机器性能下降甚至系统失稳。因此,精确地辨识永磁同步电机的参数成为了一项亟需解决的问题。
目前,国内外已有许多学者对永磁同步电机参数辨识问题展开了广泛而深入的研究。参数辨识的方法主要分为两种:离线辨识和在线辨识。离线辨识主要有DC电流延迟、AC静态方法和矢量控制方法等,但是这类辨识方法需要在电机保持稳定状态时进行,不适用于电机实际运行的场合,因此离线辨识电机参数的意义不大。在线辨识主要有最小二乘法及其拓展算法、模型参考自适应方法、遗传算法以及群体智能优化算法、基于人工神经网络的参数辨识方法、扩展卡尔曼滤波法等。文献[4]提出了一种基于模型参考自适应控制理论的多参数识别方法,采用逐步参数辨识的方法以解决电压方程秩缺陷问题。文献[5]利用遗传算法设计了一种电机多参数估计方法,然而该算法计算量大且需要较多的时间资源。文献[6]将混沌人工鱼群算法与BP神经网络相结合,克服了BP神经网络收敛过早的问题,具有一定的指导意义。
随着数据的增长,递推最小二乘法会出现“数据饱和”现象,使得新采集的数据对参数的估计值更新作用不大,当参数发生变化时,递推最小二乘法就会无法跟踪这种变化,从而导致在线辨识参数失败。加入遗忘因子后的递推最小二乘法实现了对数据的时变加权操作,削弱了过去观测数据的作用,增强了新采集数据对参数辨识的更新作用,从而使算法的跟踪能力进一步增强。然而,目前的研究大多采用固定遗忘因子的方式进行参数辨识,当遗忘因子设置过大时算法的跟踪能力下降,趋近于1时退化为普通的递推最小二乘法,当遗忘因子设置过小时算法的跟踪能力得到提高,但是参数辨识结果又会出现较大的波动。
针对传统辨识方法的不足,本文提出了一种可变遗忘因子的递推最小二乘法的永磁同步电机参数辨识方法,该辨识方法在递推最小二乘法的基础上,加入可以动态变化的遗忘因子,提高了算法的跟踪能力和稳态性,从而达到精确快速辨识的目的。
1 永磁同步电机模型
PMSM通常采用矢量控制的闭环控制方法,该方法通过坐标变换,将三相定子电流解耦为励磁的直轴电流和产生转矩的交轴电流,从而直接控制励磁和转矩。在-同步坐标系下,电压方程可以表示为:

式中:u、u分别为、轴电压;为定子电阻;i和i分别为、轴电流;L、L分别为、轴电感;ω为电机电角速度;ψ为永磁体磁链。
对于表贴式永磁同步电机,轴电感和轴电感相同,即L=L=L,所以可以将式(1)改写为:

以、轴电流为状态变量,式(2)可写为:

假设系统的采样周期足够小,可以将式(3)进行离散化处理,则有:
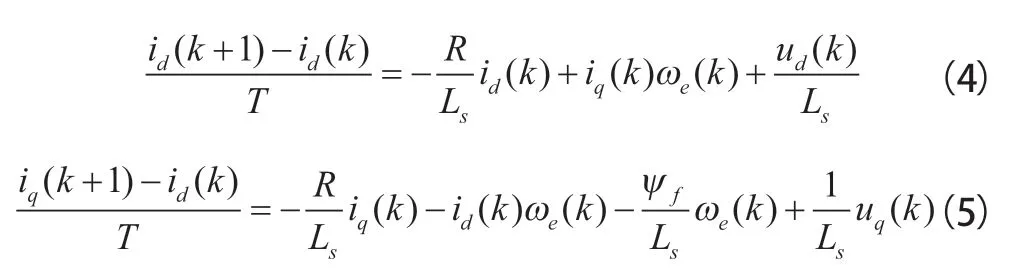
式中:表示系统运行时的第个时刻;为系统的采样周期。为了同时辨识电机的、L、Ψ,选用式(5)进行算法的设计和计算,将式(5)简化为最小二乘形式,则有:
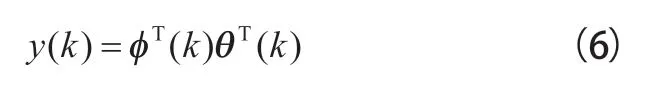
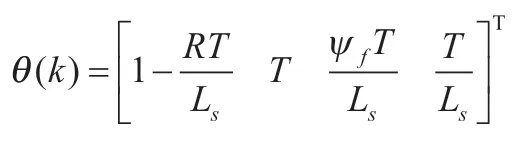
由上式可知,通过采用带遗忘因子的递推最小二乘法,对待辨识矩阵实时在线辨识,即可求出永磁同步电机的定子电阻、电感、永磁体磁链。
2 最小二乘法理论
最小二乘法自1975年由高斯在形体运动轨道预报研究工作中提出,因其简单易于理解的优点,得到了许多专家学者的支持和研究,被广泛应用于系统参数估计中。随着理论知识的不断更新,又涌现出很多基于最小二乘法的扩展算法,例如递推最小二乘法、遗忘因子递推最小二乘法、递推增广法、偏差补偿法等,这些方法都可以应用于线性定常系统以及包含时变参数的线性系统中。
2.1 遗忘因子递推最小二乘法
当被辨识的参数发生突变时,传统的递推最小二乘法可以通过周期性地重置协方差矩阵来进行参数跟踪。然而如果被辨识的参数变化缓慢,递推最小二乘法就有其局限性,随着数据量的增加,协方差矩阵和增益矩阵就会变得越来越小,对参数估计矩阵的修正能力下降,从而导致新采集的数据对参数估计的作用很小,最终导致实时参数辨识失败。为了防止数据饱和带来的参数迟滞问题,通常采用带遗忘因子的递推最小二乘法。取目标函数为:

式中:为参数估计的总次数;为参数估计的次数;为遗忘因子,一般取0.9~1。结合递推最小二乘法的推导过程,其算法的迭代公式如下:
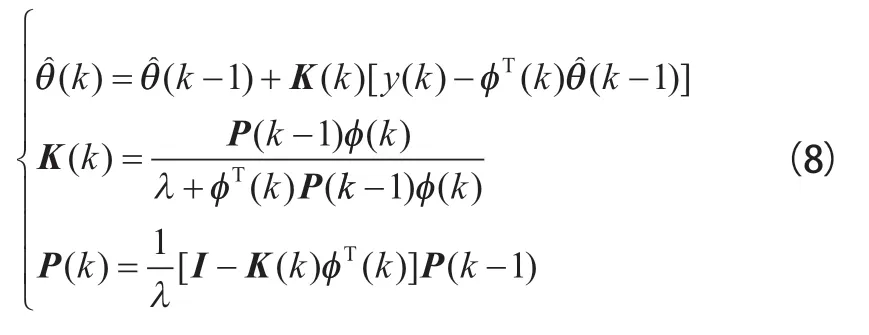
式中:(0)、 (0)一般需要提前确定。通常直接定义(0)=,为单位矩阵,为一个充分大的正实数,取值范围在10~10之间; (0)=,取充分小的正实向量或零向量。
2.2 可变遗忘因子递推最小二乘法
在固定遗忘因子的递推最小二乘法中,遗忘因子常常被设置为固定不变的值,也就意味着对数据进行了时变加权,最新采集的数据用1加权,以前个采样周期的数据用λ加权,不断削弱过去采集数据的作用,增强当前新采集数据的作用。但是无论如何选择遗忘因子的初值,算法的跟踪能力和稳态性都无法保证是最优的,总是会牺牲一部分算法的能力。为了解决此问题,将遗忘因子动态函数化,则有:
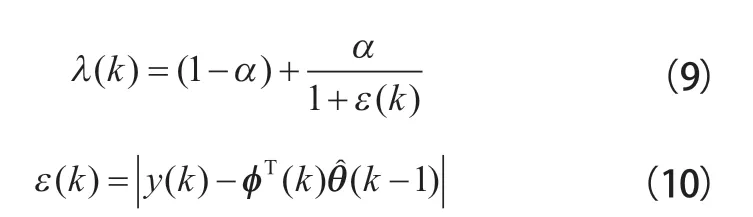
式中:为可调参数,其取值范围为0.9≤<1;()为当前时刻实际模型和理论模型的差值,其大小与可变遗忘因子()直接相关,代表了参数辨识的性能好坏。当()=0时,()=1,算法退化为普通的递推最小二乘法;当()较大时,()的值变小,参数辨识的跟踪能力增强,使算法快速收敛,达到快速跟踪参数变化的目的;当()的取值较小时,()的值增大甚至趋近于1,算法的跟踪能力下降,同时稳定性得到提高。结合固定遗忘因子的递推最小二乘法的递推公式,该算法的迭代公式可以表示为:
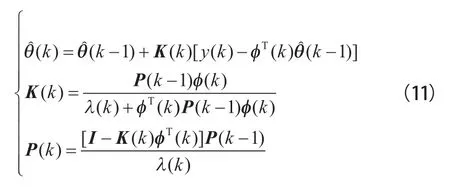
3 仿真验证
3.1 定参数仿真
对于永磁同步电机而言,经常采用矢量控制的方式建立闭环系统,加上参数辨识模块就构成了如图1所示的系统参数辨识框图。其中位置和速度测量模块用来获取电机的转速ω和转子电角速度θ,转速ω用于转速环的反馈,转子电角速度θ用于坐标变换。

图1 永磁同步电机参数辨识总体框架
为了测试永磁同步电机在恒定电机参数条件下参数辨识的效果,建立如图1所示的仿真模型,其中PMSM模块为Simulink集成的模块,只能通过仿真运行前的静态框进行离线设置,一旦仿真运行时,参数不可改变。PMSM的转动惯量为0.003 kg•m,极对数为4,定子电阻为0.958 Ω,交直轴电感L和L均为8.5 mH,转子磁链ψ为0.1 827 Wb,仿真时间为0.5 s,仿真步长为0.005 s。通过对算法和系统的仿真调试选取=0.96。首先电机以额定转速启动,0.2 s时突然施加2 N的负载,观察变遗忘因子最小二乘法的辨识效果,如图2所示。
由图2可知,采用变遗忘因子递推最小二乘法对PMSM的电阻、电感、磁链进行在线辨识,最终都能够得到比较准确的结果。由于电感的估计值较小,在参数辨识的前期会出现较大的波动,在50步的时候收敛到稳定值。电阻和永磁体磁链辨识的结果几乎接近预先设置的固定值,能满足参数辨识的要求。

图2 电机固定参数辨识结果
3.2 变参数辨识
根据文献[10]提出的PMSM改进模型,采用自定义模型的方法建立电机的仿真模型,由电机的电压方程和电磁转矩方程,将PMSM模型用S-Function函数的方式来实现,采用i=0的矢量控制方法建立的仿真模型如图3所示。

图3 矢量控制方法仿真模型
在仿真实验中,通过外部接入定子电阻、交直轴电感和永磁体磁链来设置PMSM的真实参数,实现参数可调化;通过仿真将运行时得到的电压、电流等数据,保存到MATLAB的工作区间;然后经过编写的参数辨识函数完成对电机参数的估计。其中遗忘因子动态函数中的取值要根据算法的跟踪能力和抗噪声的干扰能力进行考虑,通过对算法和仿真调试,最终选取遗忘因子动态函数中的为0.96。在仿真初始时刻,电机的各种参数设置为:=0.5 Ω,L=8.5 mH,ψ=0.17 Wb。
假设每次仿真过程中只改变一个参数值,在500步时参数值变化为=0.7 Ω,L=8.25 mH,ψ=0.19 Wb。
仿真设置RLS算法的协方差(0)为106,参数(0)为(10)[1, 1, 1],在仿真过程中加入均值为0、方差为0.5的正态分布信号,仿真时间为0.5 s,仿真步长为0.005 s,转动惯量为0.001 kg•m,极对数为4。观察RLS各种辨识算法的参数辨识效果,如图4所示。其中RLS表示普通递推最小二乘法,FFRLS表示遗忘因子固定不变的递推最小二乘法,VFFRLS表示遗忘因子可变的递推最小二乘法。
由图4可知,当电机的参数在500步的时候发生变化,普通的RLS算法由于受到数据饱和的影响,随着步数的增大,新采集的数据对参数估计值()的更新作用不大,从而导致RLS算法无法及时地跟踪参数变化后的值,最终实时估计参数失败。而VFFRLS算法和FFRLS算法都能快速跟踪参数的变化,经过800步的递推,参数的估计值都非常接近真实值,在递推的过程中可以明显地观察到VFFRLS算法的收敛速度比FFRLS算法更快,可见通过对遗忘因子的动态调整能够有效地提高算法的收敛速度,稳态精度也满足系统的要求,进一步提高了算法的跟踪能力和稳定性。
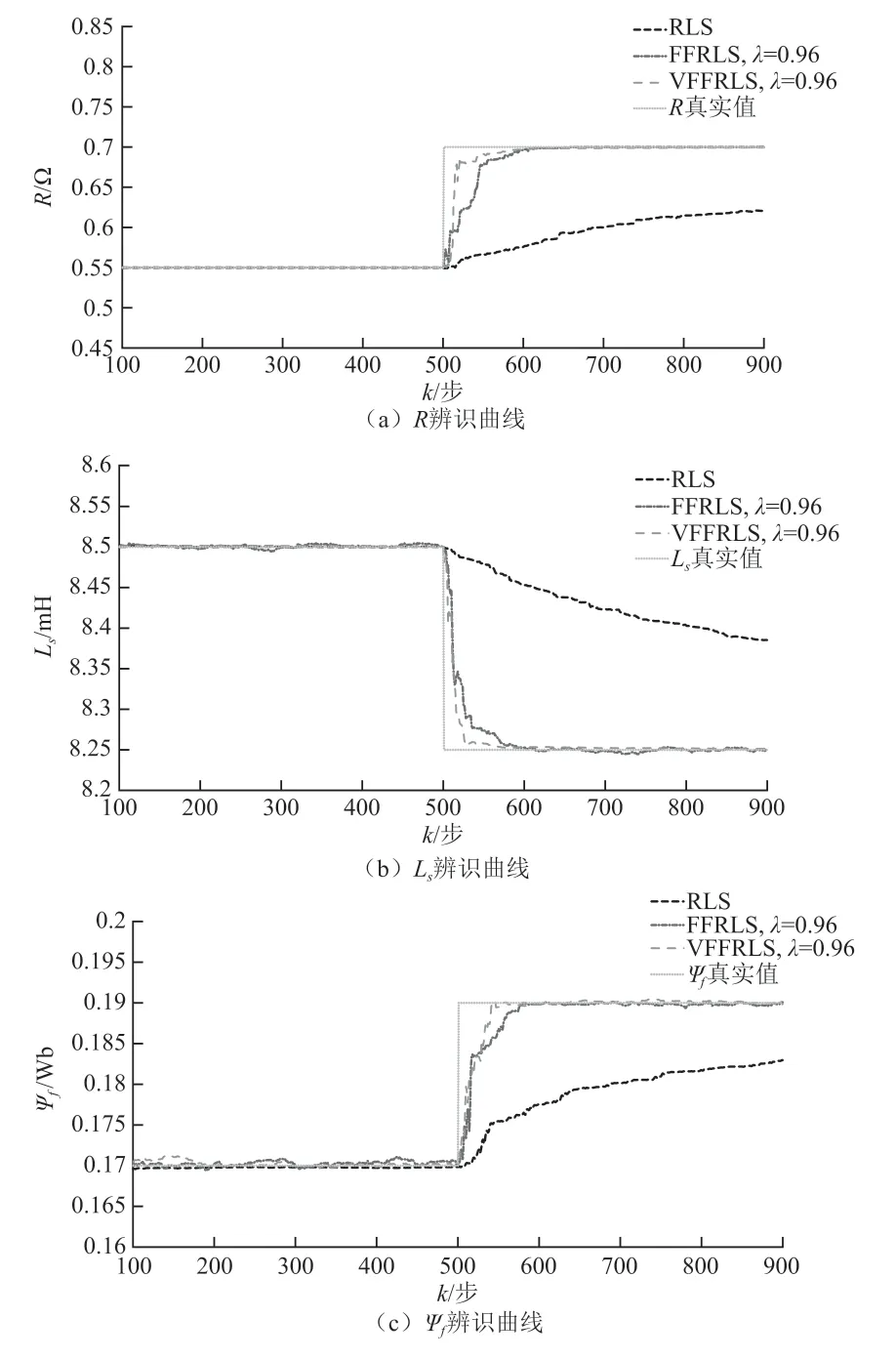
图4 电机参数可变辨识结果
4 结 语
本文在传统的递推最小二乘法的基础上,提出了可变遗忘因子递推最小二乘法辨识算法,实现了对永磁同步电机定子电阻、电感和永磁体磁链的在线估计。根据实际的模型和理论模型的差值,建立动态变化的函数,实时调整()的取值,有效地解决了传统RLS算法出现的数据饱和问题。仿真结果表明,改进的RLS算法与传统的最小二乘法和带遗忘因子的递推最小二乘法相比,收敛速度更快,具有较好的动态跟踪性能,兼顾了算法的收敛速度和辨识精度,进一步提高了算法的综合性能。
注:本文通讯作者为朱立军。
