交换BCK-代数的新型软（素）理想

黄 昱，廖祖华

1.无锡太湖学院 基础课教学部，江苏 无锡214064

2.江南大学 理学院，江苏 无锡214122

非经典逻辑及相关代数结构是人工智能的数学基础之一，其中的BCK/BCI-代数自Imai等提出以来，不断得到学者们的广泛研究。Xi把模糊集应用于BCK-代数,并给出BCK-代数的模糊理想、模糊关联理想等概念。彭家寅把扰动模糊集应用于BCI-代数中，研究了BCI-代数的扰动模糊-理想。软集的理论是处理不确定性问题的重要数学工具之一。Jun 等把软集应用于BCK/BCI-代数，提出软BCK/BCI-代数及其软子代数和软理想等概念。Khademan等在超BCK-代数中研究了模糊软正关联超BCK-理想。

交换BCK-代数是BCK-代数的重要子类，它可以构成一个下半格。Iseki给出了交换BCK-代数的素理想的概念。素理想在交换BCK-代数结构的研究中起重要作用。Jun等研究了交换BCK-代数的模糊素理想和可逆模糊理想。本文利用文献[11]将参数集赋予代数结构的思想方法，提出了交换BCK-代数的新型软素理想的新概念，这与通常的交换BCK-代数的软素理想不一样，通常的软集代数中，参数集可以没有代数结构，但初始集合必须有代数结构，且参数的像必须是初始集合的子代数（理想等）。而本文定义的新型的软集代数，是参数集必须有代数结构，但初始集合可以没有代数结构，而且这种新型软集代数比通常的软集代数结果更深刻。

在已有的亚BCI-代数的新型软理想的研究基础上，进一步研究了交换BCK-代数的新型软理想的若干性质。

1 预备知识

本章给出交换BCK-代数、软集等下面要用的相关定义和定理。

一个（2,0）型代数(,*,0)是交换BCK-代数当且仅当下列等式成立：

（1）*=0

（2）*0=

（3）(*)*=(*)*

（4）*(*)=*(*)

设是交换BCK-代数，在中定义关系：*=0 ⇔≤，则(;≤)是一个偏序集。

是交换BCK-代数当且仅当(;≤)是一个下半格且对∀,∈，有∧=*(*)。

（亚BCI-代数）一个(2,0)型代数(,*,0)如果满足条件∀,,∈，有：

（1）*0=

（2）*=0

（3）(*)*=(*)*

则称为一个亚BCI-代数。

（软集）设是一个初始集合，是参数集，⊆，()是的幂集，设:→()为一个映射，则称(,)是上的软集，也称为的软集。

（新型软理想）设是一个亚BCI-代数，:→()是一个软集，若∀,∈，满足：

（1）(0)⊇()

（2）()⊇(*)⋂()

则称是的一个新型软理想，记为(,)。

（有界BCK-代数）若BCK-代数中的一个元素满足∀∈,有≤，则称是有界BCK-代数。在有界BCK-代数中，把*记作N。

（两个软集的合成）设是亚BCI-代数，(,) 和(,) 分别为的两个软集。定义(◦,)：

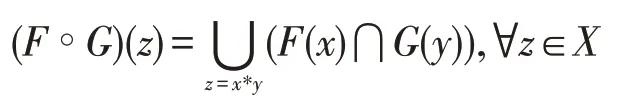
则(◦,)是的软集，并称◦为两个软集的合成。

（软集的限制并）设(,)和(,)为上的软集，若软集(,⋂)满足：

（1）⋂≠∅；

（2）∀∈⋂，有()=()⋃()。

则称(,⋂)是软集(,)和(,)的限制并，记作(,⋂)=(,)∪(,)。

（关联BCK-代数）设是BCK-代数，如果对∀,∈，有*(*)=，则称是关联BCK-代数。

（素理想）设是交换BCK-代数，是的理想且满足∀,∈，若∧∈有∈或∈，则称为的素理想。

（对偶软集）设:→()，↦()为一个软集，则称A:→()，↦A()={|∈()}为的对偶软集。设:→()，↦()为一个软集，则称H:→()，↦H()={|∈()}为的对偶软集。

设为亚BCI-代数，则下列结论成立：

（1）:→()为的新型软理想的充要条件是∀∈，A()≠∅为的理想。

（2）:→()是一个软集，则∀∈，()≠∅为的理想的充要条件是H为的新型软理想。

设为亚BCI-代数，:→()为一个软集，则是的新型软理想的充要条件是的-水平集H={|()⊇,∈()}≠∅为的理想。

设是交换BCK-代数的理想，则下列条件等价：

（1）是素理想；

（2）对于的任意理想和，若⋂⊆，则⊆或⊆；

（像与原像）设、为两个亚BCI-代数，是初始集合，()是的幂集，:→是一个映射，:→()，:→()均为软集，∀∈，∈，定义：

则()、()分别是和上的软集，称()为的像，()为的原像。

（同态与满同态）设、是两个亚BCI-代数，映射:→，若∀,∈，有(*)=()*()，则称为到的同态。当是满射时，则称为到的满同态。

设、为两个亚BCI-代数，是初始集合。:→为一个同态映射，:→()，:→()为两个软集，若为的新型软理想，有()为的新型软理想。

设、为两个亚BCI-代数，:→为一个满同态映射，:→()为软集，则为的新型软理想的充要条件是()为的新型软理想。

（-不变性）设、为两个集合，:→是到的映射，是上的软集，∀,∈，当()=()时，有()=()，则称是关于-不变的。

设、为两个亚BCI-代数，是初始集合。:→为一个同态映射，:→()为软集且是关于-不变的，若()为的新型软理想，则为的新型软理想。

设、为两个亚BCI-代数，是初始集合。:→为一个满同态映射，:→()为软集且是关于-不变的,则为的新型软理想的充要条件是()为的新型软理想。

2 交换BCK-代数的新型软理想

本章给出交换BCK-代数的新型软理想与偏序之间的关系以及它在软集运算下的性质。

设是亚BCI-代数，∀,∈，如果满足*(*)=*(*)，则称是一个交换亚BCI-代数。

注：由定理1 知，定义的交换亚BCI-代数就是交换BCK-代数。因此，下面主要讨论交换BCK-代数的新型软理想的性质。

是交换BCK-代数，是的新型软理想，若≤，则()⊇()。

若≤，则*=0，由是新型软理想，得()⊇(*)⋂()=(0)⋂()=()。

设是交换BCK-代数的新型软理想，且*≤，则()⊇()⋂() 。特别地，如果=0，则()⊇()。

因为*≤，由定理12 知，(*)⊇()。又是的新型软理想，得()⊇(*)⋂()⊇()⋂()。特别地，若=0，则()⊇()⋂()=()⋂(0)=()。

设是有界BCK-代数，且是的新型软理想，则()=()⋂(N)，∀∈。

设是有界BCK-代数，且是的新型软理想，则≤，有()⊇()；*≤，有(*)⊇()。因此()⊆()⋂(N)。又由是的新型软理想，得()⊇(*)⋂()。

因此，()=()⋂(N)。

设是交换BCK-代数，是的一个软集，如果∀,∈,有(*)⊇()⋂()，则称为的新型软代数。

定理15是交换BCK-代数的新型软理想，则是的新型软代数。

∀,∈，由是BCK-代数的新型软理想，有(0)⊇()，且(*)⊇((*)*)⋂()=((*)*)⋂()=(0*)⋂()=(0)⋂()=()⊇()⋂()。

设是交换BCK-代数，若是的新型软理想，则(,)=(,)。

综上所述，(,)=(,)。

（1）设H是的软集（=1,2），则(∪H)=()⋃()。

（2）设H是X的软集（=1,2），则(∪H)⊆()⋃()。

设是交换BCK-代数，(,)和(,)分别为的两个软集。定义(Δ,)：

则(Δ,)是的软集，并称Δ为两个软集的合成。

是的新型软理想的充要条件是Δ=且(0)=。

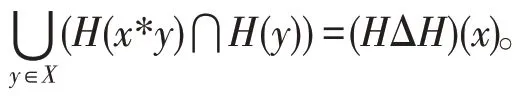
必要性：∀∈，(0)=⊇()。

因∀∈，有=∧，于是中的元素均有分解式=∧成立，所以上述定义是合理的。

设和是交换BCK-代数的两个子代数，(,)和(,)分别为的两个软集。则：

3 交换BCK-代数中软集的零化子

本章给出了交换BCK-代数中软集的零化子的新概念及相关性质。

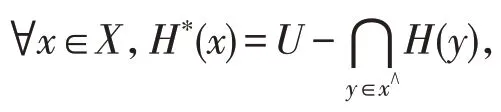
当参数集固定时，两个软集的限制交（并）与扩展交（并）重合，因此定理21就没有区分。

设和是交换BCK-代数的两个软集，则有：

（1）(0)⊇()，∀∈；

（2）如果≤，则()⊆()；

（3）如果⊆，则⊆；

（4）⊆，其中表示()；

（5）=；

（6）(⋃)⊆⋂；

（7）(⋂)=⋃；

（8）⋂⊆◦；

（5）在（4）中用替换得⊆，又⊆，由（3）得，⊆，因此=。

（6）因,⊆⋃，由（3）得，(⋃)⊆且(⋃)⊆，所以(⋃)⊆⋂。

（7）因⋂⊆,，由（3）得，,⊆(⋂)，所以⋃⊆(⋂)。又,⊆⋃，由（3）得，(⋃)⊆,(⋃)⊆，所以，(⋃)⊆⋂⊆⋂。由（3）和（4），得(⋂)⊆(⋃)⊆⋃。综上，(⋂)=⋃。

（8）和（9）由定理19可得。

设是交换BCK-代数的一个新型软理想，如果=，则称是的新型对合软理想。

有界交换和关联的BCK-代数的每个新型软理想都是新型对合软理想。

4 交换BCK-代数的新型软素理想

本章给出了交换BCK-代数新型软素理想的新概念和例子，研究了它在软集运算下的性质及等价刻画。

设交换BCK-代数，是的一个软集，如果满足下列条件：

（1）是的新型软理想；

（2）∀,∈，有()⋃()⊇(∧)，则称为的新型软素理想。

是交换BCK-代数的新型软素理想，则下列条件等价:

（1）∀,∈，有()⋃()⊇(∧)；

（2）∀,∈，有()⋃()=(∧)。

（1）⇒（2）由定理3，知∧≤,。由定理12知，(∧)⊇()且(∧)⊇()，因此(∧)⊇()⋃()，再由定义22知，(∧)=()⋃()。

（2）⇒（1）显然成立。

由定理23知，下列定理成立。

是交换BCK-代数的新型软素理想的充要条件是：

（1）是的新型软理想；

（2）∀,∈，有()⋃()=(∧)。

设有初始集合={,,,,}，参数集={0,1,2,3}，在上*运算定义如表1。

表1 运算“*”Table 1 Operator“*”

可验证(,*,0)是一个交换BCK-代数。令:→()，(0)={,,,}，(1)={,}，(2)={,,}，(3)={,,}，由定义22 知，是的新型软素理想,但它显然不是通常的软素理想。

设=={0,1,2,3},在上*运算定义如例1，令:→()，(0)={0,1,2,3}，(1)={3}，(2)={0,3}，(3)={1,2,3}，由定义知，是的新型软素理想。因(1)={3}和(3)={1,2,3}不是的素理想，故它不是通常的交换BCK-代数的软素理想，因此是一个新的软代数结构。

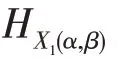
设是交换BCK-代数，则下列结论成立：

（1）:→()为的新型软素理想的充要条件是∀∈，A()≠∅为的素理想。

（2）设:→()为一个软集，则∀∈，A≠∅为的素理想的充要条件是H为的新型软素理想。

（1）必要性：由定义11和定理5得，A()≠∅为的理想。∀,∈，若∧∈A()，则∈(∧)。由是的新型软素理想，得(∧)⊆()⋃()，因此∈()或∈()，有∈A()或∈A()。因此，A()为的素理想。

充分性：由定义9 和定理5 得，是的新型软理想。∀,∈，若(∧)=∅，则显然有(∧)⊆()⋃()；若(∧)≠∅，则∀∈(∧)，有∧∈A()，由A()为的素理想，得∈A()或∈A()，有∈()或∈()，因此∈()⋃()，故(∧)⊆()⋃()。因此，是的新型软素理想。

（2）类似可证得。

设是一个交换BCK-代数，:→()为一个软集，如果对∀∈()，的-水平集H={|()⊇}≠∅是的素理想，则是的新型软素理想。

由定义9 和定理6 知，是的新型软理想。∀,∈，若(∧)=∅，则显然有(∧)⊆()⋃()；若(∧)≠∅，令(∧)=，则∧∈H，由H≠∅是的素理想，得∈H或∈H，因此()⊇或()⊇，有()⋃()⊇=(∧)。因此，是的新型软素理想。

定理28的逆命题不成立，见例3。

可换BCK-代数(,*,0)和它的一个新型软素理想同例2，取={0,1}，则有H={0}，而{0}不是的素理想，因为2×(2×3)=0，但2,3 ∉{0}。

说明通常的模糊代数与软集代数是有本质区别的。

设是交换BCK-代数，是的一个软集，下列条件等价：

（1）是的新型软素理想；

（2）∀∈，A()≠∅是的理想，且对的任意理想和，由⋂⊆A() 得⊆A() 或⊆A()；

（1）⇒（2）由定理5 知当A()≠∅时，A()是的素理想，由定理7 知，⊆A()或⊆A()。（2）⇒（3）由定理7 知显然成立。（3）⇒（1）由定理7 知A()≠∅是的素理想，再由定理5 知是的新型软素理想。

交换BCK-代数的一个新型软理想称为可逆的，如果它的软零化子也是的新型软理想。

交换BCK-代数的每个新型软素理想是可逆的。

5 交换BCK-代数的新型软素理想的像与原像

本章给出了交换BCK-代数的新型软素理想的像与原像的性质。

设、是两个交换BCK-代数，是初始集合，:→()，:→()是两个软集，:→是到的映射。

（1）当为一个同态映射时，为的新型软素理想的必要条件是()为的新型软素理想。

（2）当为一个满同态映射时，为的新型软素理想的充要条件是()为的新型软素理想。

（1）由定义22及定理8知，()为的新型软理想。∀,∈，令()=，()=∈，有()(∧)=((∧))=(()∧())=(∧)⊆()⋃()=(())⋃(())=()()⋃()()。因此，()为的新型软素理想。

（2）必要性：由定理31（1）可知结论成立。充分性：由定义22 及定理9 知，为的新型软理想。∀,∈，由是满同态映射，故∃,∈，使得()=，()=，有(∧)=(()∧())=((∧))=()(∧)⊆()⋃()=()()⋃()()。因此，为的新型软素理想。

设、是两个交换BCK-代数，是初始集合，:→是到的映射，:→()为软集且是关于-不变的。

（1）当为一个同态映射时，()为的新型软素理想的必要条件是为的新型软素理想。

（2）当为一个满同态映射时，()为的新型软素理想的充要条件是为的新型软素理想。

6 结束语

本文提出并研究了交换BCK-代数的新型软（素）理想，获得了一系列的结果。其中，引进软集的新的运算及偏序关系对交换BCK-代数的新型软（素）理想进行刻画，是本文的特色。今后将进一步利用本文的思想和方法研究亚BCI-代数的其他理想。