小样本负载序列的结构化预测方法

刘春红，张志华，焦 洁，程 渤

1.河南师范大学 计算机与信息工程学院，河南 新乡453007

2.智慧商务与物联网技术河南省工程实验室，河南 新乡453007

3.北京邮电大学 网络与交换技术国家重点实验室，北京100876

云计算是一种按需付费的计算范式，对提高云平台资源利用率、降低用户成本具有重要的作用。弹性资源管理是云平台实现按需服务的关键，基于负载预测的自动伸缩技术被经常用于弹性资源管理中，以实现资源的动态提供和释放。因负载预测的结果为系统提供决策依据，故如何构建准确性高、时效性强的负载预测模型，成为当前云平台弹性资源管理需要解决的关键问题。

目前，负载预测方法成为云计算研究的热点，取得了一些研究成果。常见的有采用传统的时间序列预测模型和当前流行的机器学习模型等，这些方法利用单个负载序列的历史信息构建预测模型，或者建立多元负载序列预测模型，并取得了较好预测效果。然而大规模云平台许多任务的运行周期都相对较短，本文将任务的运行时长较短的视为小样本负载序列，由于其具有历史数值少的特点，这使得任务负载序列提供建模的先验信息较少，导致现有负载预测方法的性能受到影响，因此如何从短负载序列中获取更多有价值的信息，成为提高预测模型性能的挑战。

由于云平台中每个虚拟机（virtual machine，VM）上运行着多种应用程序，每个应用程序在运行过程中需要同时消耗各种资源（如CPU、内存、磁盘、I/O），以保证程序的正常执行。图1 表明了消耗的多种负载序列之间存在内在的相关性。因此，为解决上述问题，本文从多维负载间关系出发，提出多变量负载序列结构化预测方法（structured prediction of multivariable workload sequences，SP-MWS）。该方法的核心在于利用多维负载类型之间的结构化信息，提高小样本数据的预测精度，并实现多种类型负载的同时预测。首先，采用MIC 和信息熵进行负载类型的度量，选择相关性强的负载类型；然后，将相关负载序列同时输入到TNR-MTL（trace-norm regularization multi-task learning）模型，实现结构化信息的挖掘，并完成多种负载的同步预测。同时从可解释性角度对预测模型的决策依据进行分析，得出每种变量对预测模型的贡献度。所提方法的创新性在于，将任务运行过程中使用的多维资源间的内在联系引入到预测模型中，实现信息共享，有效弥补了小样本数据信息不足的缺陷，提高了模型的预测性能。

图1 VM中的各种资源Fig. 1 Various resources in VM

1 相关工作

许多学者从时序角度建立基于时序的负载预测模型，分为单变量预测模型和多变量预测模型。

对于单变量预测模型，如Calheiros等利用经典的差分自回归移动平均模型（auto regressive integrated moving average，ARIMA）来预测未来工作量需求，实现对非平稳时间序列的有效预测。随着人工智能的兴起，大量的机器学习方法被用于负载预测中。Liu 等提出一种基于负载特征识别的预测方法，根据负载变化的速度自动分配线性回归（linear regression，LR）或支持向量回归（support vector regression，SVR）模型；Islam等提出基于人工神经网络（artificial neural network，ANN）和LR 的资源需求预测模型，并将这两种方法与滑动窗口相结合；Nguyen等利用长短时记忆神经网络（long short-term memory，LSTM）实现连续区间平均负载的多步预测。

根据文献调研，云平台中从多变量角度实现资源预测的工作相对较少。Hieu 等提出一种基于多资源预测的虚拟机整合算法，利用多元LR估计输入和输出数据间的映射，以提高云数据中心的性能。该资源预测的模型本质上属于线性模型，故不适应多个变量间存在非线性关系的场景。Tran 等利用模糊技术进行资源的预处理，然后选择相关变量作为LSTM 模型的输入，实现多变量时间序列的预测。由于深度学习模型需要大量的数据和时间，故当负载的历史信息较少时，模型的预测性能受到影响，且未达到资源的及时响应。

2 多变量负载序列结构化预测方法

为对云平台中运行周期较短应用程序的多种负载进行同时、有效的预测，提出了多变量负载序列结构化预测方法。流程图见图2 所示，包括四部分：数据收集、数据预处理、相关负载类型的获取、结构化预测模型的构建及预测输出。

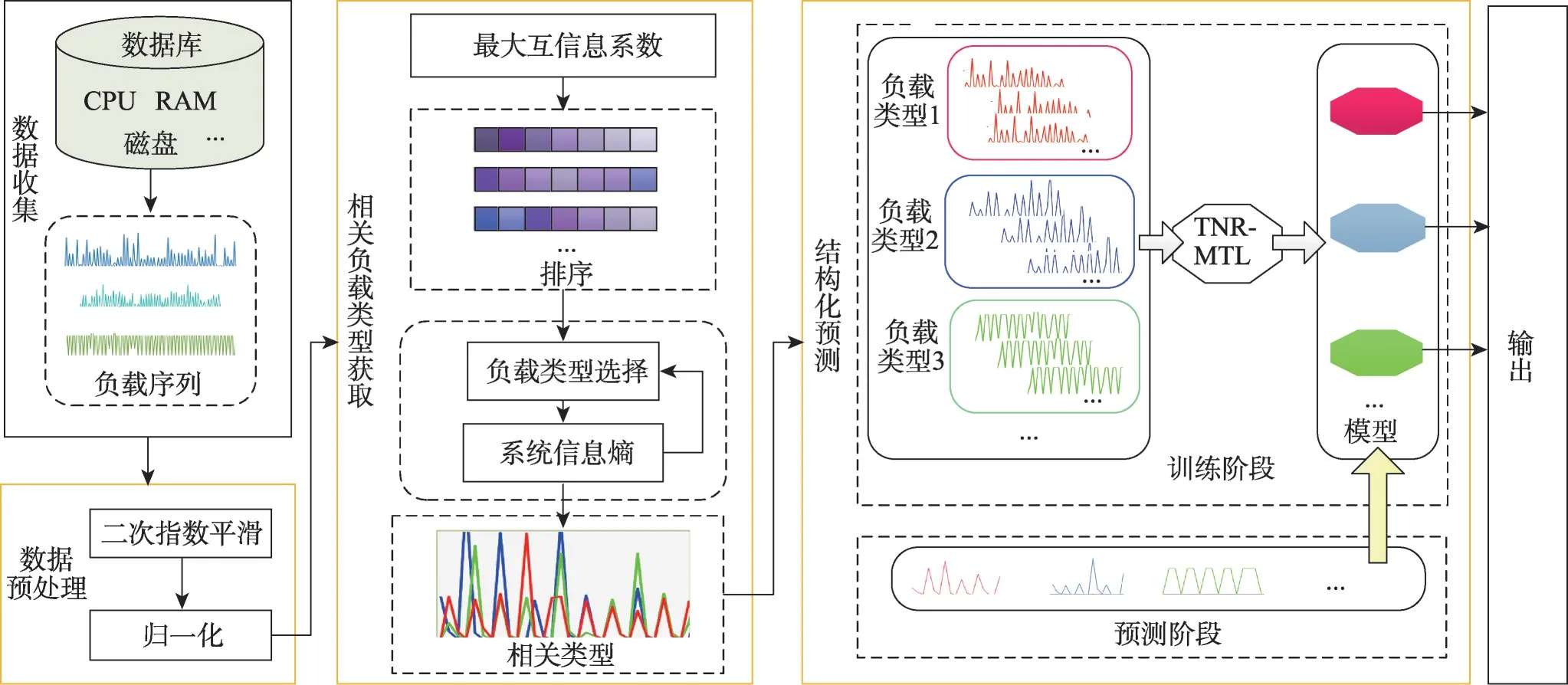
图2 SP-MWS流程图Fig. 2 Flowchart of SP-MWS

首先，数据收集主要指从数据库收集任务在运行过程中使用到的多种资源（CPU、内存和磁盘等）的历史信息以及其他信息。其次，在数据预处理阶段，采用二次指数平滑法和归一化对得到的负载进行预处理，去除噪声和序列间差异。然后，在相关负载类型获取阶段，采用最大互信息系数法，同时从线性和非线性角度计算资源间的相关性，引入信息熵判断模型信息量的增长情况，结合二者的结果实现相关负载类型的选择，这是在离线状态下进行的。最后，在线状态下，构建结构化预测模型，采用TNR-MTL模型作为预测模型，将上阶段获得的多种负载类型分别当作一个学习任务，利用训练数据完成模型的训练后，预测数据按照负载类型，输入到各自对应的学习任务中，从而完成运行周期较短任务多种资源的同时预测和输出。

2.1 数据预处理

2.2 相关负载类型获取

针对小样本负载序列预测过程中样本信息量不足而导致预测性能受限的问题，为了增加预测模型所需的先验信息，将任务的多维数据信息引入到负载预测模型中。由于负载序列之间的相关度越大，其蕴含的结构化信息越多，故不同类型负载序列间的相关程度，将直接影响预测模型的性能。目前有学者从信息论角度研究多变量时间序列间的相关性，但对于云负载的类似研究工作比较少。此外，对于不同类型的负载，它们各自选择的相关负载类型可能存在差异，比如与CPU 变化密切相关的负载类型不一定与内存的变化也密切相关，因此为实现多种资源类型的同时预测输出，必须保障预测模型所含的信息量能够满足、适合每一种待预测负载类型的建模，即应选择与CPU和内存都相关的负载类型。

为实现上述目标，本文将MIC 和信息熵结合使用。对于MIC，由于其能够衡量两个变量的线性函数关系和非线性函数关系，对数据分布没有严格要求和假设，同时具有计算复杂度低、鲁棒性高的特点，被用于衡量任务运行过程中所使用的各种负载之间的相关性；在信息论中，熵表示随机变量的不确定性，不确定性越大，熵越大。信息熵可理解为要消除或降低这种不确定性，仍需引入多少额外信息量的度量。信息熵越大，说明此时系统自身所提供的信息量较少，则需要引入更多的信息；相反，信息熵越小，说明此时系统自身所含的信息量多，需要引入的信息量少。因此，本文依据信息熵值的增减，判断添加的相关变量为预测模型提供信息量的情况。

首先分别计算其他负载与每个待预测负载的MIC值。根据MIC的大小进行排序，即MIC值越大，表明这两种负载类型间的关系越紧密；MIC值越小，表明二者越疏远；然后选择每种待预测负载的前位，从中将超过半数待预测负载共有的负载类型，依次添加到预测模型中，并计算此时模型的信息熵，信息熵最小时所对应的负载类型即为获取到的最终相关负载类型。设任务有种负载，种待预测负载，∈{1,}，详细计算过程如下：

计算MIC 值，然后分别对每种待预测负载和其他负载的MIC值从大到小进行排序。

归一化后得预测结果评价矩阵：

计算此时预测系统信息熵InE，见式（2）：

重复步骤3，直到=时终止。

求出InE最小时所对应的，即为最终获得相关负载类型。

以上过程全部在离线阶段完成。

2.3 结构化负载预测及输出

为充分利用具有相关性的负载序列间的结构化信息，对每个任务构建基于核范数正则化的多任务学习模型（TNR-MTL），用滑动窗口进行预测。针对上述得到的+种负载序列，将每一种负载序列分别作为TNR-MTL模型中的一个学习任务，其中在每一个学习任务内，包含该负载类型下的多个任务负载序列，每次将滑动窗口大小的采样点作为输入数据，相应下一时刻的值作为输出值。模型完成训练后，测试集数据根据各自的负载类型，选择训练好的预测模型，完成多个负载的结构化预测。TNR-MTL模型的目标函数见式（3）。

其中，=[,,…,w]表示权重矩阵，w是第个学习任务的权重向量；为模型中学习任务的个数，X和Y分别代表第个学习任务的输入和输出，表示超参数，控制权重矩阵的秩。因矩阵的秩可反映该矩阵中变量间的相关性，矩阵秩越低，表明变量相关性越强，故对权重矩阵进行核范数约束，使得矩阵呈现低秩状态，即将每个任务多种负载序列的信息投影到一个共享、合理、相关程度高的低维子空间。在该模型空间中，建模所需的通用领域知识被多个学习任务共享，提升了每个学习任务的学习性能，从而实现同一个任务中所有负载类型的联合学习，以及多种负载的同时预测。

3 实验及结果分析

3.1 实验数据与实验设计

本文采用大型通用云平台Google数据集进行实验验证。它是Google数据中心公开的2011年5月期间的监控日志，记录多个计算节点29天的运行情况，包括约672 074个作业，2 600万个任务。其中数据集中的task resource usage 表记录任务运行过程中消耗各种资源信息。实验数据如表1所示。

表1 实验数据对象Table 1 Experimental data objects

实验共分3 组：（1）相关负载类型的获取；（2）实验预测效果展示，包括所提方法预测性能的分阶段展示多种方法对比的实验结果和分析，其中对比实验中分别选择两个不同大小的滑动窗口，并从时间性能和预测性能两方面进行对比；（3）负载贡献度分析。

本实验中回归预测精度的评定指标采用均方根误差（root mean square error，RMSE）、平均绝对误差（mean absolute error，MAE）、平均相对误差（mean relative error，MRE）和对称平均绝对百分率（symmetric mean absolute percentage error，SMAPE）。

3.2 相关负载类型的获取

任务在运行过程中需要消耗多种资源，为提高多变量负载序列预测的准确性，对多种资源间的相关性进行分析，选择具有相关性的负载类型。首先分别计算CPU、内存和磁盘与除自身以外的其他剩余负载之间MIC 值。为得到公平的结果，实验时选择100 个任务进行相同的操作，然后对结果进行统计，得到大多数情况下每种待预测负载与其他负载的相关性，按从大到小的顺序排序，结果如表2 所示。可以看出每种待预测负载与其他负载类型之间的相关程度不完全相同。

在计算模型信息熵时，本次实验取每种待预测负载相关性排行榜中，除待预测负载外，MIC值排行前三的负载类型。由表2 可得，对于CPU 是mean-DiskIO、aMem、maxDiskIO；对于内存是meanDiskIO、aMem、maxMem；对于磁盘是aMem、meanDiskIO、maxDiskIO，如表2中粗体部分。

表2 待预测负载与其他负载类型的相关性统计结果Table 2 Statistical results of correlation between load to be predicted and other load types

因meanDiskIO 在CPU 和内存中MIC 值均处于第一位，MIC值越大，表明这两种负载类型间的关系越紧密。故将meanDiskIO首先添加到负载预测模型中，计算此时模型信息熵；依次类推，将aMem 和maxDiskIO分别添加到模型中，并计算每种情况下的模型信息熵，结果如图3 所示。为方便介绍，将负载添加过程分为几个阶段：变量个数为3 记V3（包括CPU、内存和磁盘），变量个数为4 记V4（包括CPU、内存、磁盘和meanDiskIO），变量个数为5记V5（包括CPU、内存、磁盘、meanDiskIO和aMem），以及变量个数为6 记为V6（包括CPU、内存、磁盘、meanDiskIO、aMem和maxDiskIO）。

图3 不同阶段信息熵Fig. 3 Information entropy at different stages

由图3 可得，随着负载序列变量个数增加，系统信息熵逐渐递减，信息熵越小，说明此时系统所含的信息量多，将多维信息添加到预测模型中，有助于信息间的交叉验证，提高预测的准确性。故将V6所对应的负载类型作为最终获得的相关负载类型。

3.3 预测结果及分析

为验证随着相关变量的添加，预测模型的准确度也不断提升，对不同阶段进行负载预测。以CPU的预测结果为例，结果见表3。

表3 不同阶段的预测结果Table 3 Forecast results at different stages

从表3中可以得出，对于所有评价指标，都在V6时取得了最低误差值；除了RMSE 指标存在V4 阶段的误差值高于V3阶段外，剩余其他指标中，误差下降的顺序均沿着V3、V4、V5的方向，故从整体上看各种误差呈现下降趋势。这说明了随着相关负载类型的引入，确实能够补充建模时所需要的有效信息，提高预测精度，而且表中预测精度提升的幅度与图3中信息熵值降低的幅度呈正比。

由于多数任务的运行周期较短，故设置大小不同的滑动窗口，模拟不同长度的时间序列，进行实验，其中滑动窗口的大小分别为60和30，即将待预测时刻的前60 个采样点作为已知数据，和将待预测时刻的前30个采样点作为已知数据。为验证所提方法的性能，将SP-MWS 与多元线性回归、SVR和LSTM进行对比。这里SVR方法指事先需要采用多变量相空间重构技术，然后利用SVR模型进行预测，为方便描述，将其记为P-SVR；LSTM 方法主要采用的是多变量LSTM模型（multivariate LSTM，M-LSTM）。在进行多变量重构过程中，6 种变量（CPU、内存、磁盘、meanDiskIO、aMem 和maxDiskIO）的时延分别为2、1、2、2、2、2，嵌入维分别为6、7、2、2、2、2；LSTM 模型的隐藏层神经元个数为50，迭代次数均为500次。

（1）滑动窗口为60

表4～表6是所提方法和其他方法在RMSE、MAE、MRE和SMAPE四种性能指标的对比结果。

表4 不同方法下CPU预测误差对比Table 4 Comparison of CPU prediction errors under different methods

表5 不同方法下内存预测误差对比Table 5 Comparison of memory prediction errors under different methods

表6 不同方法下磁盘预测误差对比Table 6 Comparison of disk prediction errors under different methods

虽然在表5的RMSE指标中，所提方法的预测误差略大于P-SVR，但是SP-MWS 在剩余其他评价指标，以及其他待预测负载类型的所有评价指标中，都取到了最小的预测误差，故从整体上看，SP-MWS 的预测结果是最优的，其次是多元线性方法或P-SVR方法，预测效果相对较差的是M-LSTM。分析可知，SP-MWS对各种资源建立预测模型时，将它们的模型参数信息用秩约束到共享特征子空间，从而使得建模信息之间具有高相关性，并实现信息的共享，弥补了各自样本信息不足的缺点，然后利用负载间的结构化信息进行预测，因此取得了较好的性能；多元线性方法本质上属于线性回归，而在实际的云平台中，负载序列之间普遍存在非线性关系，同时由于数据量较小，导致多元线性模型未能挖掘数据中隐藏的有用信息；对于P-SVR模型而言，虽然SVR适合小样本数据的预测，但是P-SVR仍属于单任务学习模型，预测过程中也只是利用了单个负载的信息，而且多变量重构时每个变量均需要确定对应的模型参数，而参数的选择和设定对于预测模型的效果具有直接的影响；M-LSTM模型属于深度学习模型，需要大量的训练数据，而当任务运行周期较短，所使用的历史数据信息相对较少时，该方法的预测误差较高。

表7 是滑动窗口等于60 时所提方法和其他方法在时间性能上的对比结果，将每种方法重复运行30次，取平均时间作为该方法的最终预测时间。

表7 不同方法下三种资源的预测时间（滑动窗口为60）Table 7 Forecasting time of three resources under different methods(sliding window is 60)

观察表7 发现，对三种资源同时预测时，多元线性方法消耗的时间是最短的，其次是SP-MWS、PSVR，时间最长的是M-LSTM。分析可知，多元线性模型的本质属于线性模型，结构比较简单，故运行速度较快；SP-MWS 利用负载间的关系，使得多种相关负载类型协作预测，达到并行输出的效果，从而用时短；而P-SVR 和M-LSTM 均需要耗费大量的时间寻找最优参数，导致模型的时间较长。虽然所提方法的时间性能不如多元线性方法，但是SP-MWS 的预测准确度优于多元线性方法。

（2）滑动窗口为30

为进一步表明所提方法在任务运行周期较短时，也能很好地进行负载预测，将滑动窗口缩小为30。图4是不同方法对三种资源进行预测时的误差情况，表8是所提方法在滑动窗口等于30 时，和其他方法在时间性能上的对比结果。

表8 不同方法下三种资源的预测时间（滑动窗口为30）Table 8 Forecasting time of three resources under different methods(sliding window is 30)

图4 不同方法对三种资源的预测效果（滑动窗口为30）Fig. 4 Prediction effects of different methods on three resources(sliding window is 30)

由图4 可得，对三种不同的资源类型，SP-MWS的预测误差在四种评价指标上均取得最小值；表8中，SP-MWS的时间性能仍位于第二。对比表7，表8中各种方法的预测时间均缩短，说明时间序列缩短时，消耗时间也缩短，所提方法缩短明显。由此验证了所提方法对小样本负载序列进行预测的可行性。

综上所述，本文方法的时间性能虽略差于多元线性方法，但预测性能优于多元线性方法；与其他方法相比，SP-MWS在时间性能和预测性能上都取得较好的预测效果。从整体上看，所提方法的性能更优，适合云平台多种短负载序列的预测。

3.4 贡献度分析

为进一步探索每个输入变量对所构建模型贡献度的大小，了解影响目标变化的原因，引入Shapley值实现各预测变量对模型预测效果贡献度的分析。它表示在实现最终目标利益的联盟中，每个局中人的相对贡献度。在多变量负载预测问题中，局中人对应了多种负载序列类型，联盟为预测模型，联盟利益则为预测模型的准确性。因此，Shapley 值可表示在实现预测模型的准确度达到较为满意的过程中，输入变量对模型预测结果贡献度的大小，Shapley 值越大，则贡献度越大。

为清晰表示各输入变量在每种待预测负载预测时的相对重要程度，将计算结果分开展示。图5是每种负载类型在预测过程中对CPU、内存和磁盘预测时的贡献度。横轴是每种负载类型的平均Shapley值，纵坐标为负载类型，按贡献度的大小进行排序。

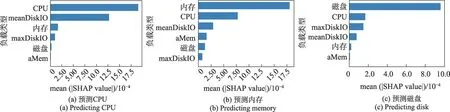
图5 各负载类型对最终预测结果的贡献度Fig. 5 Contribution of each load type to final prediction result

由图5 可知，在对待预测负载进行预测时，每种负载类型对不同待预测负载的贡献度不相同，但是都具有两个共同点：（1）所选择的负载类型，对预测模型中每种待预测负载的预测过程，都起到了不同程度的促进作用；（2）每种待预测负载历史信息的贡献度都是最大的，比如图5（a）中，在对CPU下一时刻进行预测时，CPU 负载历史信息对最终预测结果的贡献度居于首位，这也非常符合实际场景。对每个子图分别进行以下分析：

（1）图5（a）中，meanDiskIO 的贡献度排第二，然后是内存，说明除CPU历史信息外，与其他负载类型相比，影响CPU 预测结果好坏的主要因素是mean-DiskIO 和内存。虽然meanDiskIO 和内存都与CPU相关性较高，但对CPU预测来说，meanDiskIO对提高模型预测性能的促进作用相对较大。

（2）图5（b）中，贡献度排在第二位的是CPU，然后meanDiskIO，这说明除内存历史信息外，CPU 和meanDiskIO 是影响内存预测准确度的主要原因，但CPU的影响程度要大于meanDiskIO。

（3）图5（c）中，CPU 和maxDiskIO 贡献度相对较高，说明对磁盘预测而言，除其本身的历史信息外，相对重要的负载类型是CPU和maxDiskIO。

4 结束语

针对云平台中大量任务运行周期短，小样本负载序列所提供建模的先验信息少，且同一任务在运行中需消耗多种资源的情况，将任务的多维负载序列信息添加到预测模型中，有助于信息间的交叉验证。本文提出了多变量负载序列结构化预测方法。该方法采用最大互信息系数度量任务运行过程中消耗的多种资源之间的相关度，并联合信息熵完成相关负载类型的选择，使用TNR-MTL 构建预测模型，以捕捉和利用相关负载间的结构化信息。结果显示所提方法取得了较优的预测效果，同时分析了输入变量与最终预测结果之间的关系。

由于大规模云平台中负载之间的关系具有强复杂性，故下一步工作将研究多种复杂负载序列间的内在关系，并对其进行深层次的挖掘和探索，从而进一步提高预测模型的性能。