基于有限差分方法的矿区深基坑变形监测研究
2022-07-20薛广楠
薛广楠
(山东黄金集团蓬莱矿业有限公司,山东 烟台 265621)
0.引言
随着经济的不断发展和安全环保要求的不断提高,在矿区进行的各类基坑的施工规模也在不断扩大,且质量要求在提高[1]。而在很多矿产开发区,由于临近水系或降水量充足,近地表地层往往以淤泥或淤泥质黏土、粉质黏土等岩(土)层为主,这些地层的孔隙度大、含水率高,可压缩率及可塑性指数较高[2],因此其稳定性相比一般地层更差,在这些区域,基坑的施工难度更大,安全隐患也更多[3]。因此,对软土层深基坑在开挖过程中的变形情况进行精确的模拟预测,具有重要的现实意义[4]。
由于软土地层的特殊性质,为了提高预测的准确性,有学者先后提出了弹性法计算、基于HSS模型的数字模拟等方法,但是还存在着模拟参数无法动态变化(或可调整数据类别偏少)、计算数据量大等各类问题。本文针对以上问题,尤其是确定变形的初始和边界两个参数的难度较大的问题[5],提出了使用有限差分求解各向异性材料的应用方法,这是解决该难题的有效对策。对于使用有限差分方法进行数值模拟,在解决空间问题时,可将待求解的空间细分为六面体差分网格,再将六面体单位细分为常应变四面体单元。结合区域地质资料和工程要求,选取合理的模拟参数,进而开展数值模拟,再利用有限差分软件建立三维模型。通过建立的三维模型,就可以对软土层深基坑的施工过程、变形情况进行模拟与分析,进而全面掌握基坑开挖过程中的变形特征以及对支护结构稳定性的影响。
1.工程概况
拟施工区域位于某矿场开发地区,该施工区域又分为一区、二区、三区和四区4个施工区,本次选取其中施工规模最大的二号区为研究对象。该施工区的基坑计划开挖深度23.3m,宽度19.2m,基坑全长94.2m。需要说明的是,该施工区域的地表情况较为复杂,周边有进出矿区的主干道2条,且临近区域还分布有养殖池4处。因此,该深基坑施工的安全性显得特别重要,对其变形预测的精准性要求较高。
对施工区域的地层进行钻孔取样,并结合以往地质资料进行综合分析,确定了该区域的地层分布及岩性特征。该区域主要由淤泥或淤泥质黏土、粉质黏土等岩(土)层组成,属于典型的软土地层施工区域。其地层及岩性情况介绍如下:
(1)素填土(A-1):该层顶部零散覆盖一层0—0.1m的混凝土;下部0.1—6.7m为黄色黏性土层,其间夹杂约7.5%的砾石,其平均厚度为3.53m。由于该层压实作用较差,因此需要支护。
(2)淤泥或淤泥质黏土(B-1):分布深度为2.2—8.2m,平均厚度约3.12m,该层大部呈深灰色,富含有机质呈流塑状且有异味,同样为欠压实层且不能自稳。
(3)粉质黏土(B-2):分布深度4.4—27m,平均厚度约14.43m,该层为本次基坑施工的主要层位。大部分呈黄褐色,可塑性及黏性较好,同样为欠压实层且不能自稳。
(4)含砾粉质黏土(B-3):其分布较为零散,主要呈黄褐色或黑色,可塑性及黏性较好,含有约13.2%的砾石。
(5)砂岩(C-1):该岩性仅在14.2—27m的深度范围内有局部分布;整体呈褐色,实测饱和单轴抗压强度值为42—87MPa,该层硬度较大且能够自稳。
(6)砂砾岩(C-2):该岩性在21.9—27m的深度范围内有局部分布;整体呈深褐色,实测饱和单轴抗压强度值为43.2—88MPa,该层硬度较大且能够自稳。
(7)微风化/强风化灰岩(D-1):该岩性在17.2—27m的深度范围内大量分布,平均厚度约8.7m;大部分呈灰褐色,为隐晶质结构且发育有节理与裂隙,实测饱和单轴抗压强度值为33.2—95.3MPa,该层硬度较大且能够自稳。
2.软土层基坑变形特征及数值模拟
2.1 变形特征
综合分析施工区域的地层资料和岩性特征,可以得出该区软土地层的基本特点:(1)灵敏度高,即当外部受力条件改变时,其土体原有结构亦随之变化,从而导致土体强度降低,但是稳定一段时间后,其强度又会逐渐恢复,但所需恢复时间一般较长;(2)透水性差,此次开挖的主要地层为粉质黏土层,其天然空隙比大于1,说明其透水性较差,要重点考虑地下水对施工产生的影响并依据施工情况进行人工排水;(3)黏土层的可压缩率高,即强度较低,故而其承载能力较差,不能将其作为持力层,需要及时进行支护,同时还需要注意其产生的不均匀沉降。
对此类软土层深基坑进行数值模拟,其变形特征与按照初始模量计算得出的变形情况往往存在较大差异,这是由于常规的模拟实验得出的压缩模量要比软土层的卸荷模量小很多。所以随着基坑开挖的深度越来越大,基坑周边会出现不均匀沉降,而坑底也会出现塑性和弹性隆起,且其卸载和变化的特征受地质条件、设计方案和施工等多重因素的影响。一般来说,需要综合考虑安全和经济等条件,采用桩锚或内支撑等刚性支护结构,确保施工安全。
2.2 数值模拟
数值模拟的原始计算是从最终细分的四面体单元开始,可将四面体的四个顶点分别编号为a、b、c、d,而m代表与节点对应的面,设其内部某一点的速度大小为vi,mi为四面体外表面单位法向量分量,四面体的体积为V、表面积为S,通过高斯定理进行计算,如式(1)所示:

在常应变单元中,vi为线性分布,mj在各外表面上为常量,1和(1)分别为节点变量和面变量,如式(2)所示:

再对四个顶点分配质量以及受力,那么通过虚功原理可得出对应顶点的不平衡力,之后再通过中心差分进行计算,如式(3)和式(4)所示:

最后由运动速率求解某步时下单元应变增量,在这个过程中,对于应变增量的求解,可采用本构方程求解单元应变增量,再将各步时应力增量叠加,最终求出总应力,如式(5)所示:
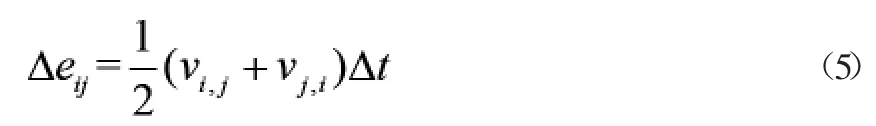
对于边界参数的确定,可采用摩尔库伦强度准则,设τn为某点的抗剪切强度,c为土体粘聚力,σn为土体颗粒受到的正应力,φ为土体内摩擦角,如式(6)所示:

3.模型建立
本次实验选取的二号施工区域,计划施工尺寸为94.2m×19.2m×23.3m,基于深基坑的固有特性,其在2—4倍开挖深度、3—5倍开挖范围的情况下,可能发生的变形情况最为严重,因此,在模型建立时,设定的深基坑尺寸为122m×72m×55m,所建立的模型共包括节点86875个、单元89734个。建立模型的主要土体的物理力学参数(如表1所示):

表1 模型中主要土体的物理力学参数
依据施工特点,对施工过程中的6个工况进行模拟,分别是开挖至3.0m、7.2m、13.4m、16.2m、19.3m、23.3m。由于工况3为挖掘规模最大的一次施工,且开挖层位为典型的软土层层位,而工况6为基坑施工完成时的状态,因此主要展示工况3和工况6的开挖情况。通过建立的三维模型,可以对施工过程中的基坑形态、地连墙位移、钢支撑轴力变化、地表沉降等诸多情况进行模拟,下面介绍典型模拟内容。
3.1 地连墙水平位移模拟
工况1至工况6的最大模拟位移结果分别是:1.92mm、2.58mm、5.32mm、6.32mm、7.79mm、8.31mm。其中工况3和工况6的模拟情况(如图1所示)。由此可见,地连墙的水平位移与开挖深度呈正相关关系,同时变形区域也逐步向基坑深部发展,因此,在开挖过程中,首先要及时进行支护,其次要尽可能进行分段及分层开挖,并严格控制基坑暴露时间,进而有效控制基坑变形。

图1 地连墙的水平位移模拟
3.2 地连墙垂直位移模拟
工况1至工况6的最大模拟位移结果分别是:2.32mm、4.88mm、7.62mm、7.99mm、8.23mm、8.86mm。工况3和工况6的垂直位移模拟情况(如图2所示)。模拟显示自工况4开始,位移增速变缓,这主要是随着开挖规模最大的工况3的结束以及支护结构的架设,基坑的稳定性逐渐趋好。

图2 地连墙的垂直位移模拟
3.3 地表沉降模拟
工况1至工况6的最大模拟位移结果分别是:3.52mm、4.88mm、8.13m、9.89mm、13.23mm、13.39mm。工况3和工况6的地表沉降模拟情况(如图3所示):

图3 地表沉降模拟
需要注意的是,在进行工况模拟的过程中,要检查最大不平衡力的变化趋势,因为该指标是判断模型是否达到平衡状态的重要依据:如果模拟数值趋近于0,则说明模型已恢复到平衡状态。本次模拟的6个工况的最大不平衡力情况(如图4所示),各个工况施工完成后的数值均趋近于0,说明均达到平衡状态。

图4 最大不平衡力模拟
4.实验对比分析
本次基坑施工的风险等级为二级,监测仪器主要采用数字水准仪、全站仪、测斜仪和轴力计等设备,依据《建筑基坑工程监测技术规范》等标准设定监测的项目如下:支护结构的水平和竖直位移监测,布设监测点72个。周边地表沉降情况监测,布设监测点80个,采取16×5的设置方式,即设置16排、每排5个监测点位。土体深层水平位移监测,布设监测点16个。此外还有地下水位监测点8个;支撑轴力、裂缝监测等点位12个。
监测周期设定为:在开挖过程中,开挖深度小于5m时每2天监测1次,开挖深度大于5m时每天监测1次;开挖完成后,第一周每天监测1次,第二周每2天监测1次,之后视情况逐渐延长。同时,不同的监测项目还根据实际情况设定了报警值,严防事故发生。
4.1 实测结果与仿真情况对比
将地连墙的水平及垂直位移的实测数据与仿真数据进行对比,两者均实现了较好拟合,对比情况(如图5所示):

图5 地连墙的水平与垂直位移的实测值与模拟值对比
对于基坑周边地表的沉降情况,选取其中变化幅度较大的4个点位(即代号为DQ的一排点位)与仿真情况进行对比。对比情况(如图6所示):

图6 地表沉降实测值与模拟值对比
4.2 对比结果分析
从图6中可以看出:工况1至工况3的位移变化幅度相对较大,而自工况4开始位移变化趋势放缓。这是因为工况1至工况3正在对软土层进行开挖,且开挖深度大、施工时间长;而自工况4开始,逐渐进入砂岩和灰岩等硬质地层施工,且支护结构逐步完善,因此变化幅度必然减小。
总体来说,通过实测结果与仿真情况的对比分析,不论是地连墙的水平及垂直位移,还是周边地表沉降情况,模拟值与实测值均保持相同的变化趋势,且实现了较好的拟合。地连墙的位移模拟值与实测值的平均绝对误差为0.44mm,均方根误差仅为0.48mm;而周边地表的沉降情况的模拟值与实测值的平均绝对误差为0.39mm,均方根误差仅为0.49mm。两者的均方根误差均小于0.5mm,说明数值模拟较为准确地反映了基坑的变化情况,预测模型是可靠的。
5.结束语
本文以某矿区软土层深基坑工程为背景,介绍了软土层深基坑的工程特点和施工难点,提出了基于数值模拟的方法,选取合理的土体参数并建立三维模型,对软土层深基坑的变形趋势进行预测,对支护结构的有效性进行验证,最后通过与实测数据对比,发现模拟数据与实测数据实现了较好地拟合,且预测误差控制在合理范围之内。因此,该方法具备较强的实用性和可靠性,对于软土层深基坑的施工提供了一种有效的预测和指导手段,对于工程建设具有重要的现实意义。
