分布式光伏与风电机组LVRT及电流限幅环节的等值建模
2022-07-20陈海东潘学萍孙晓荣和大壮雍成立
陈海东,潘学萍,黄 桦,孙晓荣,和大壮,雍成立
(1. 河海大学能源与电气学院,江苏南京 211100;2. 南京工程学院电力工程学院,江苏南京 211167)
0 引言
当前随着分布式新能源机组的持续并网,电力负荷的动态特性已发生了显著变化,传统负荷模型不再适用于新型电力系统仿真分析的需求,亟需构建含分布式新能源机组的综合负荷模型[1-2]。目前在研究主动配电网的等值模型时,一般将配电网中各类分布式新能源机组等值,将其与传统负荷模型并联作为主动配电网的等值模型结构[3-6]。然而由于主动配电网中分布式新能源机组类型不同、控制方式各异,且需满足主动配电网的动态无功支撑需求,接入主动配电网的分布式新能源机组通常被要求具备低电压穿越(LVRT)能力[7-8]。故建立含LVRT控制的多类型分布式新能源机组的通用模型为当前的研究热点。
由电力电子设备主导的分布式新能源机组,其控制器存在限幅、死区等环节;且正常情况下的PQ解耦控制与LVRT 控制之间存在切换等离散事件;文献[9]还指出双馈风电机组(DFIG)为混杂动态系统,具备非线性特征。故含多类型分布式新能源机组等值建模的难点在于对非线性环节进行等值建模。
目前针对诸如换流器等非线性系统的等值建模研究较少。文献[10]从逆变器为典型非线性仿射系统的角度出发,研究了逆变器降阶与微分流形的相似性关系,将微分同调应用于逆变器降阶中,提出了单变量微分同调判据。文献[11]针对含多状态变量的并网逆变器,提出了基于广义哈密顿作用量的同调判别标准,并依据能量守恒得到了实用化同调判据。在模型等值方面,文献[12]通过对每台换流器下垂控制中的状态变量进行等效变换,提出了计及多换流器动态交互作用的等值单机非线性模型,但在等值建模时仅对多台换流器的控制环节进行了等效变换,未涉及非线性环节的等值。文献[13-14]通过解析方法,对风电场/光伏(PV)场站内机组的LVRT动态全过程进行了解析等值,进一步将解析等值结果与其他环节的物理模型相结合,获得等值机的模型及参数。然而上述文献仅对LVRT 过程进行了等值处理,对于如限幅环节等非线性环节的等值未见研究。还有研究采用参数辨识方法获得非线性模型参数,如文献[15-16]基于模型参考自适应方法/扩展卡尔曼滤波法,对永磁同步发电机转子电阻等电气参数进行了辨识。然而文献[17]指出,非线性系统在离散切换瞬间,微小的参数变化可能导致较大动态差异,基于此刻响应数据进行参数辨识将产生较大的误差,即无法通过参数辨识获取准确的非线性模型参数。
针对上述问题,本文分析了分布式新能源机组受多激励影响的非线性环节响应特性,采用非机理建模方法获得非线性环节的等值模型。以主动配电网为例,建立多类型分布式新能源机组的通用模型。模型等值时将线性环节采用参数辨识的方法获取模型重点参数;非线性环节采用解析方法推导其在不同扰动程度下的解析结果,进一步采用拟合法获得非机理等值模型。最后对某实际配电网进行建模仿真,验证了所提方法的可行性。值得注意的是,本文基于PSCAD/EMTDC 平台推荐的分布式新能源机组模型及参数进行分析研究,但所提方法同样适用于不同新能源厂商提供的机组模型及参数。
1 多类型分布式新能源机组的通用模型及LVRT控制
1.1 多类型分布式新能源机组的通用模型结构
DFIG、直驱永磁风电机组(DDPMSG)和PV的详细模型[18-19]见附录A图A1。由于电网侧扰动下分布式新能源机组的动态特性受换流器及其控制环节影响,且各类分布式新能源机组的控制策略相近,为此文献[3]提出了构建逆变型并网的多类型分布式新能源机组的通用模型,但其构建的模型未计及分布式新能源机组LVRT的动态特性。
本文提出的可表达多类型分布式新能源机组LVRT 动态特性的通用模型如附录A 图A2所示。由于DFIG、DDPMSG 以及PV 的主要区别在于原动机侧,因此图A2所示通用模型中将原动机侧等效为恒功率源,其有功、无功功率参考值分别为Pgref、Qgref;经直流电容、逆变器、RLC 滤波电路后通过输电线路(电阻为RL和电抗为XL)并网。锁相环(PLL)用以获得机端电压相位;有功功率和无功功率均采用双环控制方式。下面对计及分布式新能源机组LVRT 动态过程的低电压有功、无功管理环节和电流限幅环节进行详细介绍。
1.2 低电压有功管理环节
低电压有功管理环节根据分布式新能源机组的端口电压对Pgref进行调整,调整后的有功功率参考值为λPgref(λ为分布式新能源机组的有功调整系数)。不同新能源厂商关于λ的设置方法不尽相同,本文选用PSCAD/EMTDC 平台中分布式新能源机组的有功调整系数λ进行分析,其波形如图1 所示。图中:U为分布式新能源机组的端口电压;Un为系统额定电压。

图1 分布式新能源机组的有功调整系数Fig.1 Active power adjustment coefficient of distributed new energy units
1)DFIG的λ为:
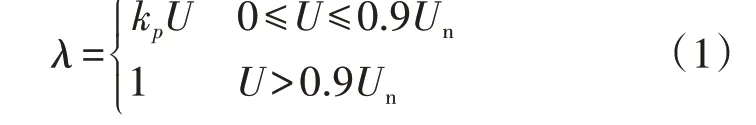
式中:kp为有功系数。
2)DDPMSG的λ为:
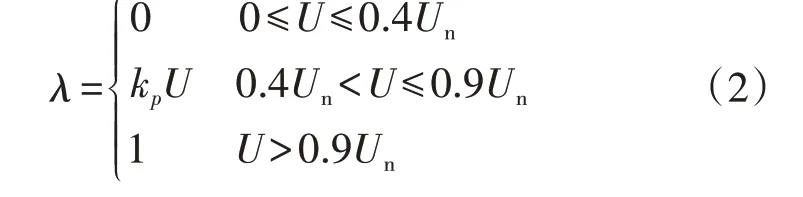
3)PV的λ=1。
电压跌落期间,分布式新能源机组的有功功率与其端口电压跌落深度相关;故障清除后分布式新能源机组的端口电压开始恢复,由图1 可知其有功功率也开始恢复,功率恢复速率与电压恢复速率一致。
1.3 低电压无功管理环节
低电压无功管理环节的目的是确定分布式新能源机组在LVRT 期间的无功附加电流iqLVRT。iqLVRT与换流器稳态控制下的无功电流指令值之和作为分布式新能源机组的总无功电流参考值iqref。选用PSCAD/EMTDC 平台中分布式新能源机组的无功附加电流模块进行分析。
1)DFIG未设置无功附加电流模块,即iqLVRT=0。
2)DDPMSG的iqLVRT为:
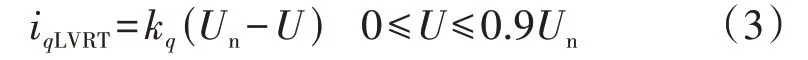
式中:kq为无功附加电流系数。
3)PV的iqLVRT为:

电压跌落期间,分布式新能源机组的无功功率与其端口电压的跌落深度相关;故障清除后分布式新能源机组的端口电压开始恢复,其无功功率也开始恢复,功率恢复速率与电压恢复速率一致。
1.4 电流限幅环节
分布式新能源机组受电力电子换流器最大电流限额Imax的影响。为保证电压跌落期间对系统的无功功率支撑,分布式新能源机组常采用无功优先控制策略,此时其最大有功电流idmax和最大无功电流iqmax满足:
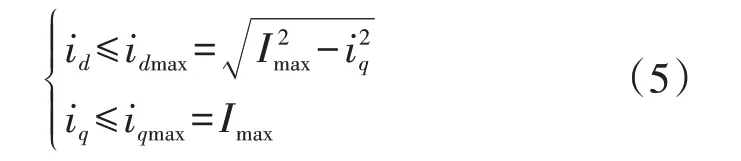
式中:id和iq分别为分布式新能源机组端口电流的d轴和q轴分量。在附录A 图A2 所示的通用模型中,电力电子换流器的低电压有功、无功管理环节及电流限幅环节都为非线性环节,其余为线性环节。
2 多类型分布式新能源机组非线性环节的等值建模
针对含多类型分布式新电源机组的主动配电网,建模时分布式新能源机组通常采用动态等值方法,即将配电网中多类型分布式新能源机组等值为1台或多台等值机组。根据图A2所示通用模型进行等值建模,线性环节中采用按容量加权平均或参数辨识等方法获取等值模型参数,而目前对于非线性环节的等值建模方法较少。本文提出受多激励影响的非线性环节等值建模方法。
2.1 低电压有功管理环节的模型聚合
由于主动配电网中各类型分布式新能源机组的并网点不同,电网侧扰动下其低电压有功管理环节的状态也不尽相同,等值建模时需计及各类型分布式新能源机组不同低电压有功管理环节状态的影响。
假设主动配电网中被等值的分布式新能源机组有n台,根据图1 可得等值机的有功功率参考值Peq.ref为:
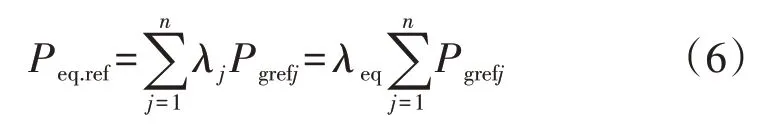
式中:λeq为等值机的有功调整系数;λj为分布式新能源机组j的有功调整系数;Pgrefj为分布式新能源机组j的有功参考值。由式(6)可以看出,λeq与各分布式新能源机组是否进入低电压有功管理环节有关。当所有被等值机组都未进入低电压有功管理环节时,各机组的λ皆为1,故λeq=1;当部分/全部机组进入低电压有功管理环节时,需根据式(6)求取λeq。


根据图2,当配电网中有n台被等值机组时,λeq可采用式(7)所示分段函数近似拟合。
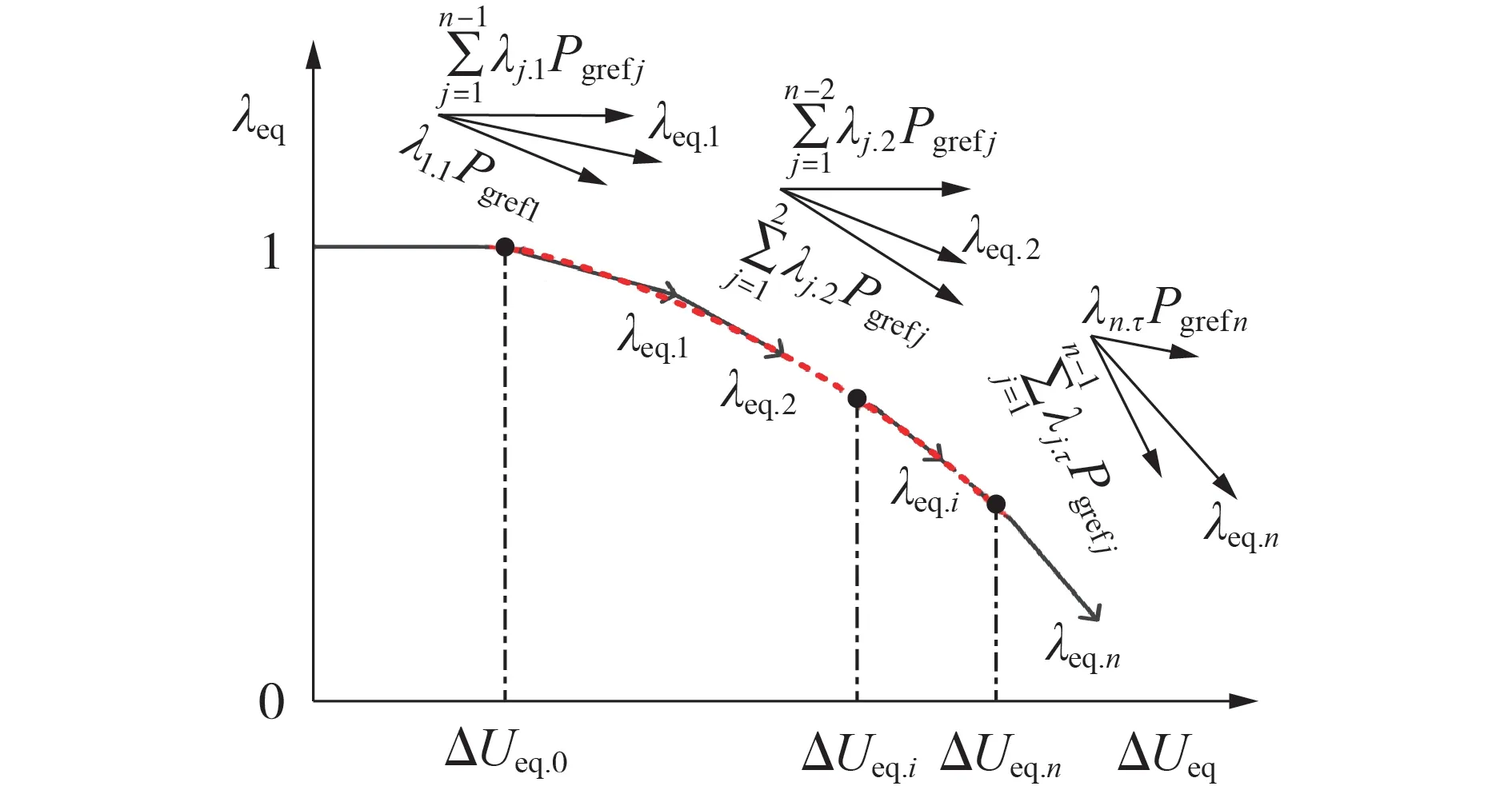
图2 低电压有功管理环节的模型聚合Fig.2 Model aggregation of low voltage active power management link

式中:ap、bp、cp、ap1、cp1为拟合系数。
当等值母线电压的变化量处于[ΔUeq.0,ΔUeq.n]区间时,从图2可以看出,可采用拟合系数为ap、bp、cp的二次函数(图中的虚线)拟合等值机的有功调整系数;当所有分布式新能源机组都进入低电压有功管理环节时,λeq为关于ΔUeq的一次函数,此时拟合系数ap1和cp1均为常数。
值得注意的是,若分布式新能源机组在进入低电压有功管理环节后,有功调整系数具有分段特性,如图1 所示的DDPMSG,在端口电压跌落到0.4Un及以下时,有功调整系数恒定为0。则λeq在式(7)所示一次函数对应的等值母线电压变化区间会多出1个二次函数和一次函数。这是因为存在一部分DDPMSG 的有功调整系数为0,一部分不为0 的情况。此时多出的分段函数在形式和确定方法方面与式(7)相同,这里不再赘述。
2.2 低电压无功管理环节的模型聚合
设有n台分布式新能源机组被等值,则由式(3)、(4)可得等值机的无功附加电流为:
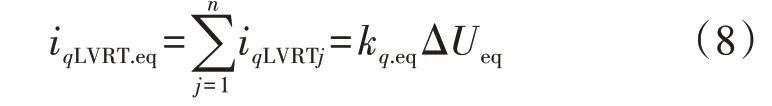
式中:iqLVRT.eq为等值机无功附加电流值;kq.eq为等值机无功附加电流系数。由式(3)、(4)可以看出:当所有分布式新能源机组都未进入低电压无功管理环节时,各机组的kq皆为0,因此kq.eq=0;当部分/全部机组进入低电压无功管理环节时,需根据式(8)求取kq.eq。
以2台分布式新能源机组为例,假设扰动1下机组1 进入低电压无功管理环节,其无功附加电流iqLVRT1=kq1ΔU1+ε1,ΔU1为机组1 端口电压的变化量,ε1为常数,kq1为机组1 的无功附加电流系数;机组2未进入低电压无功管理环节,其无功附加电流为0,此时等值机的无功附加电流为iqLVRT.eq.1=kq1ΔU1+ε1=kq.eq.1ΔUeq。随着电压跌落程度的加深,当2台分布式新能源机组都进入低电压无功管理环节时,机组1的无功附加电流仍为iqLVRT1=kq1ΔU1+ε1,机组2 的无功附加电流为iqLVRT2=kq2ΔU2+ε2(ε2为常数),则等值机的无功附加电流iqLVRT.eq.2=kq1ΔU1+ε1+kq2ΔU2+ε2=kq.eq.2ΔUeq。
根据上述结果,可得n台分布式新能源机组被等值时,iqLVRT.eq为斜率单调递增的连续折线,见附录A 图A3。由图可知,当配电网中有n台被等值时,iqLVRT.eq可采用式(9)所示分段函数近似拟合。
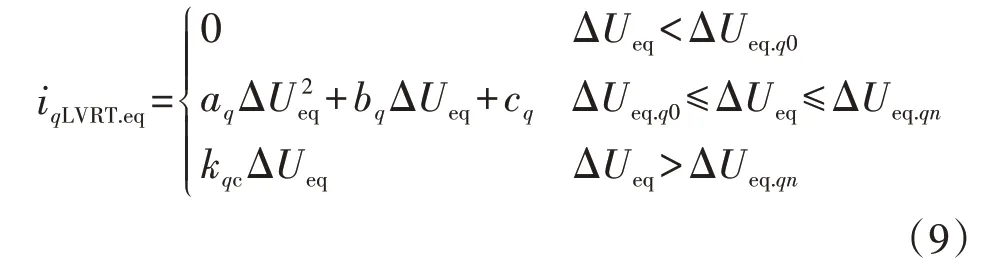
式中:ΔUeq.q0为所有分布式新能源机组都未进入低电压无功管理环节时等值母线电压变化量的门槛值;ΔUeq.qn为所有分布式新能源机组都进入低电压无功管理时等值母线电压变化量的门槛值;aq、bq、cq和kqc为拟合系数。
当等值母线电压的变化量处于[ΔUeq.q0,ΔUeq.qn]区间时,从图A3 可以看出,可采用系数为aq、bq和cq的二次函数(见图A3 中的红色虚线)拟合等值机的无功附加电流;当所有机组都进入低电压无功管理环节时,kqc为常数。
2.3 电流限幅环节的等值
当多台分布式新能源机组进行模型聚合时,需确定等值机组的电流限幅值。
1)当所有分布式新能源机组未进入电流限幅环节时,等值机的d轴和q轴电流为所有机组的对应电流之和,即:
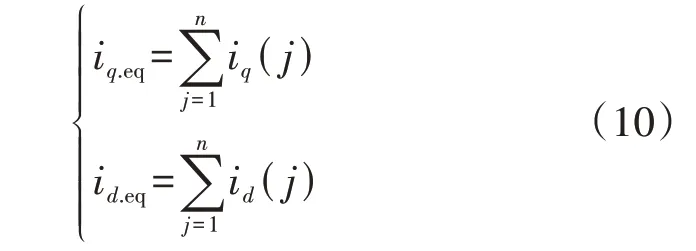
2)当部分机组进入电流限幅环节时,设有n1台机组进入电流限幅环节,n-n1台机组未进入电流限幅环节,由于采用无功优先控制,故等值机电流的d、q轴分量分别为:
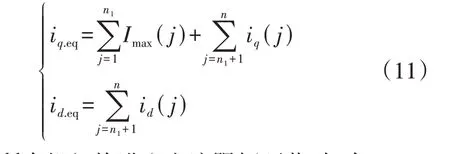
3)当所有机组均进入电流限幅环节时,有:
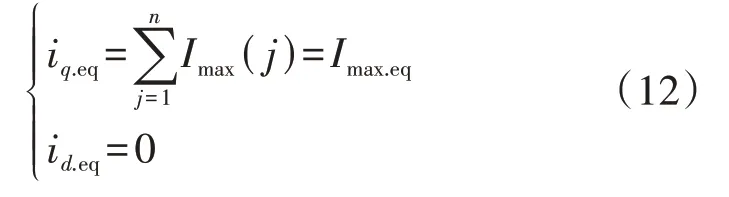
式中:Imax.eq为所有分布式新能源机组的电流限幅值之和。从式(10)—(12)可以看出:由于受被等值机组进入电流限幅环节状态的影响,等值机的d、q轴电流限幅值将不再是确定值,其会随着电压跌落深度的变化而变化。

根据图A4,可将等值机的d轴电流限幅值idmax.eq采用式(14)所示分段函数拟合。
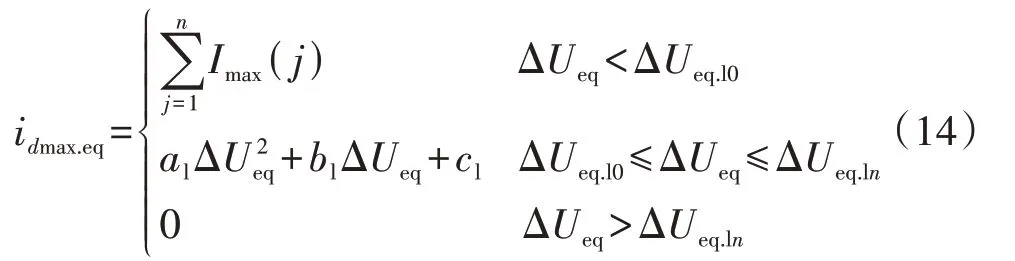
式中:al、bl和cl为二次函数拟合系数;ΔUeq.l0为所有分布式新能源机组都未进入电流限幅环节时等值母线电压变化量的门槛值;ΔUeq.ln为所有分布式新能源机组都进入电流限幅环节时等值母线电压变化量的门槛值。
3 多激励下多类型分布式新能源机组非线性环节的非机理等值建模
下面以3 类分布式新能源并网的简单算例为例,分别给出分布式新能源机组低电压有功管理、低电压无功管理以及电流限幅环节在多激励下的非机理等值建模流程。
3.1 非机理等值建模流程
以低电压有功管理环节为例,多类型分布式新能源机组低电压有功管理环节的非机理等值建模流程见图3。低电压无功管理环节以及电流限幅环节的非机理等值建模流程与图3 基本一致,这里不再赘述。
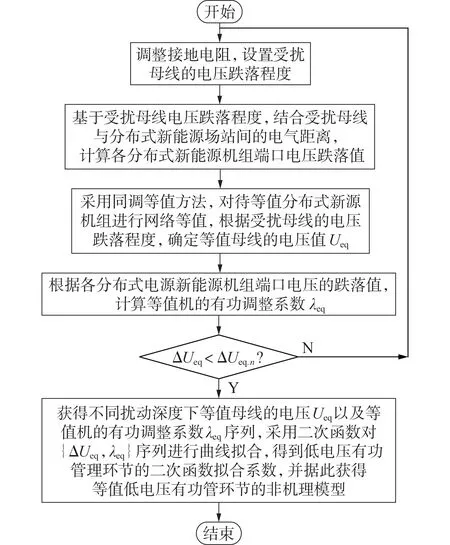
图3 低电压有功管理环节的非机理等值建模流程Fig.3 Non-mechanism equivalent modeling flowchart of low voltage active power management link
3.2 算例分析
多类型分布式新能源机组的并网接线图如图4 所示,2 台DFIG、2 台DDPMSG 以及1 台PV 接入母线B2,其额定功率均为1 MW,分布式新能源机组通过两级升压变压器接入220 kV 系统,其参数采用PSCAD/EMTDC平台推荐的典型参数。假设分布式新能源机组均采用定无功控制方式,即Qgref=0,低电压有功管理和无功管理环节分别见1.2 节和1.3 节,DFIG、DDPMSG 以及PV 的电流限幅值分别为1.1、1.1、1.5 p.u.。并网阻抗分别为Z1=0.22+j1.07 p.u.,Z2=0.58+j1.65 p.u.,Z3=2.12+j5.18 p.u.,Z4=4.71+j13.59 p.u.,Z5=6.81+j19.03 p.u.(基准容量为1 MV·A)。
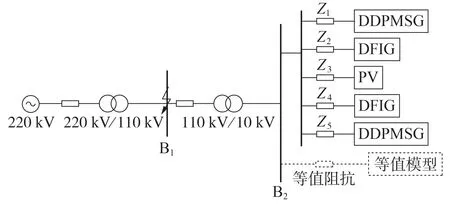
图4 多类型分布式新能源机组的并网接线图Fig.4 Grid-connected wiring diagram of multi-type distributed new energy units
进行等值建模时,首先将各分布式新能源机组采用图A2所示的通用模型结构表示,下面对各非线性环节的等值建模过程进行详细阐述。
3.2.1 低电压有功管理环节的非机理等值建模
根据图3 所示建模流程,设故障发生在母线B1处,根据各分布式新能源机组与母线B2的电气距离计算可得:当母线B2的电压跌落小于10.1%Un时,所有新能源机组都未进入低电压有功管理环节,即ΔUeq.0=10.1%Un;当母线B2的电压跌落大于等于11.8%Un时,所有分布式新能源机组都进入低电压有功管理环节,即ΔUeq.n=11.8%Un。
在母线B2处设置不同电压跌落扰动,其变化区间为[10.1%Un,11.8%Un],进而可得每种电压跌落程度下的{ΔUeq,λeq}序列,最后采用二次函数拟合该序列,二次函数的拟合结果如式(15)及图5(a)所示。
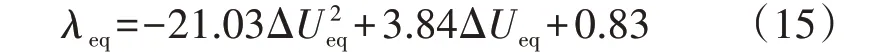
此外,由于DDPMSG 的有功调整系数存在分段特性,当母线B2的电压跌落小于60.1%Un时,所有DDPMSG 的有功调整系数都不为0;当母线B2的电压跌落大于等于61.8%Un时,所有DDPMSG 的有功调整系数都为0。因此,在母线B2设置不同电压跌落扰动,其变化区间为[60.1%Un,61.8%Un],进而可得每种电压跌落程度下的{ΔUeq,λeq}序列,采用二次函数拟合该序列,二次函数的拟合结果如式(16)及图5(b)所示。
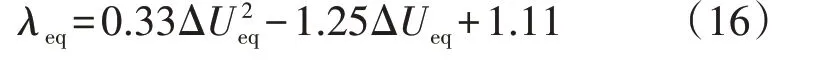
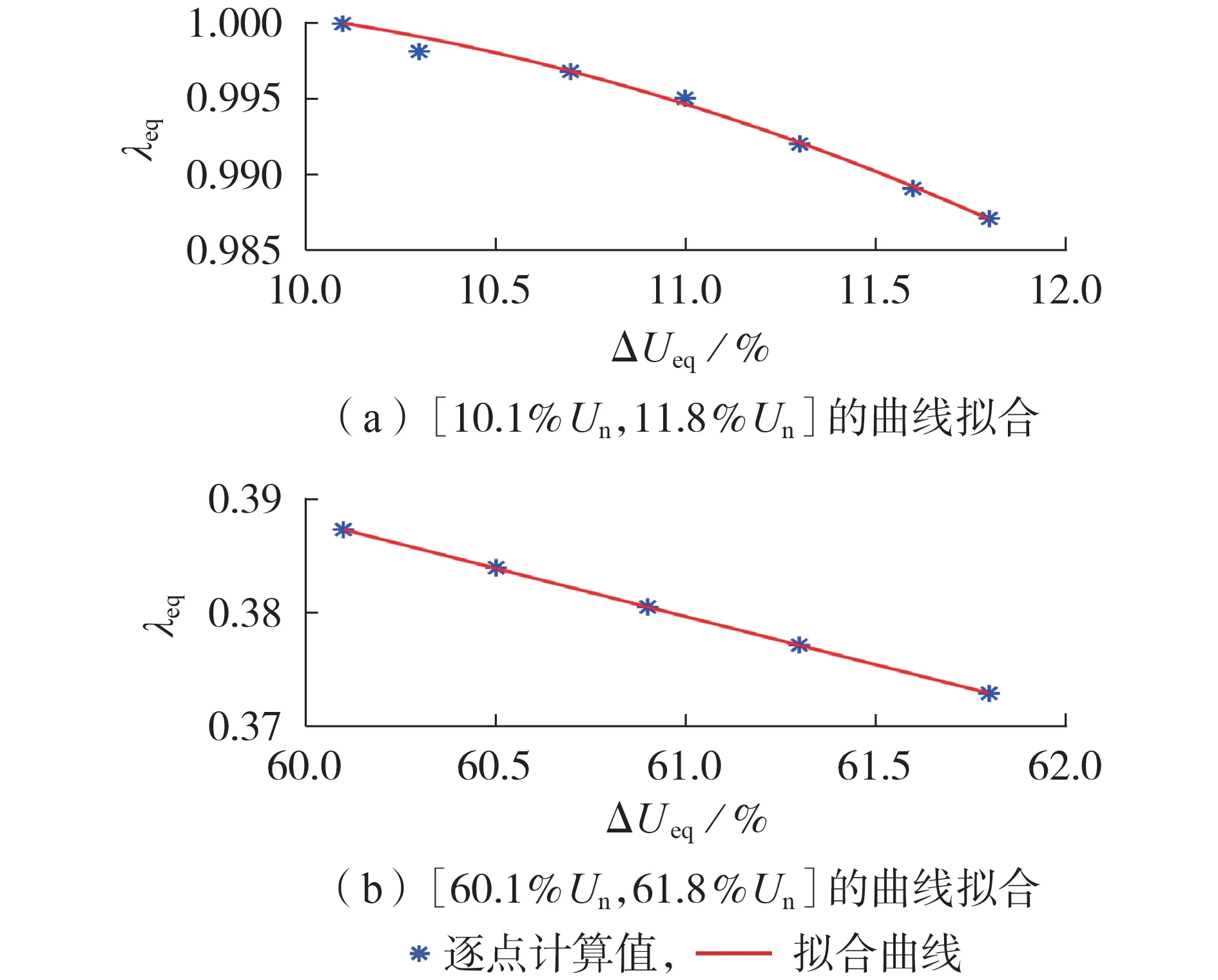
图5 有功管理环节的非机理等值建模Fig.5 Non-mechanism equivalent modeling of active power management link
3.2.2 低电压无功管理环节的非机理等值建模
采用与低电压有功管理环节等值相似的流程,可得母线B2处的电压跌落小于10.1%Un时,所有分布式新能源机组都未进入低电压无功管理环节,即ΔUeq.q0=10.1%Un;当母线B2处的电压跌落大于等于20.5%Un时,所有分布式新能源机组都进入低电压无功管理环节,即ΔUeq.qn=20.5%Un。
在母线B2设置不同电压跌落扰动,其变化区间为[10.1%Un,20.5%Un],进而可得每种电压跌落程度下的{ΔUeq,iqLVRT.eq}序列,最后采用二次函数拟合该序列,拟合结果见式(17)以及附录A图A5。

3.2.3 电流限幅环节的非机理等值建模
在母线B2处设置不同电压跌落程度的扰动,可得母线B2的电压跌落小于34.16%Un时,所有分布式新能源机组都未进入电流限幅环节,即ΔUeq.l0=34.16%Un;当母线B2的电压跌落大于等于39.41%Un时,所有分布式新能源机组都进入电流限幅环节,即ΔUeq.ln=39.41%Un。
在母线B2处设置不同的电压跌落扰动,其变化区间为[34.16%Un,39.41%Un],可得每种电压跌落程度下的{ΔUeq,idmax.eq}序列,采用二次函数拟合该序列,拟合结果见式(18)以及附录A 图A6。由图可知,idmax.eq可近似由式(18)拟合。
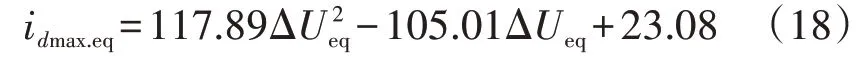
综合图5、图A5和图A6的曲线拟合结果可以看出,采用图3、图A3 和图A4 所示的二次曲线拟合方法可以较好地进行部分分布式新能源机组进入LVRT 或进入电流限幅环节时非线性环节的等值建模。
4 算例验证
将所提多类型分布式新能源机组非线性环节的非机理等值建模方法进一步应用于主动配电网中,进行机组等值建模,并将等值模型与传统负荷模型并联作为主动配电网的等值模型。
以附录A图A7所示的某实际10 kV主动配电网为例,基于PSCAD/EMTDC 平台搭建该仿真系统。设线路阻抗为0.116+j0.106 7 Ω/km,静态负荷的电阻RZ与电抗XZ的比值满足RZ/XZ=5,感应电动机负荷参数见附录A 表A1。图A7 中,分布式新能源的出力占总负荷比例的104.44%,其中DFIG、DDPMSG以及PV 的出力分别占新能源总出力的37.04%、37.04%和25.93%。
4.1 分布式新能源机组非线性环节的等值建模
首先采用图A2 所示的通用模型表示各分布式新能源机组,然后对各分布式新能源机组进行等值建模。等值时对其中的线性环节采用参数辨识方法获取重点参数,对其中的非线性环节采用本文所提等值建模方法。
在多扰动激励下,扰动设置为母线A1处发生三相短路故障,通过调整接地电阻使得母线A2的电压分别发生不同程度的跌落。根据各分布式新能源机组与扰动点的电气距离,可得等值机进入低电压有功管理环节的等值母线电压变化量门槛值分别为ΔUeq.0=10.2%Un和ΔUeq.n=11.8%Un。与此同时,可计算得到当等值母线电压的变化量处于区间[60.2%Un,61.4%Un]内时,部分DDPMSG 的有功调整系数为0。
因此,在母线A2处分别设置变化量处于区间[10.2%Un,11.8%Un]和[60.2%Un,61.4%Un]内的电压跌落扰动,得到相应的{ΔUeq,λeq}序列,采用二次函数拟合,结果见附录A 式(A1)。同理,进行低电压无功管理环节等值时,根据各分布式新能源与扰动点的电气距离,计算得到ΔUeq.q0=10.2%Un,ΔUeq.qn=21.1%Un。在此区间内根据所得{ΔUeq,iqLVRT.eq}序列,采用二次函数拟合,结果见附录A 式(A2)。进行电流限幅环节等值时,计算得到ΔUeq.l0=34.26%Un,ΔUeq.ln=40.1%Un。在此区间内根据所得{ΔUeq,idmax.eq}序列,采用二次函数拟合,结果见附录A 式(A3)。由式(A1)—(A3)可得不同电压跌落程度下非线性环节的等值参数。
4.2 主动配电网的等值建模验证
由文献[20]可知传统综合负荷模型的待辨识参数为并网等值阻抗(RCLM+jXCLM),感应电动机的定子电抗XS、初始转差率s0以及惯性时间常数H;此外还有感应电动机消耗有功占综合负荷消耗有功的比例KIM。而对于分布式新能源机组,由文献[4]可知,其重点参数为并网等值阻抗(RDG+jXDG),换流器有功控制环节、无功控制环节外环的比例积分参数Kpp、Kpi、Kqp和Kqi,以及锁相环的比例积分参数KPLLp和KPLLi,此外还有分布式新能源机组输出功率占综合负荷总消耗功率的比例KDG。由此确定15 个待辨识的参数,分别为{RDG,XDG,RCLM,XCLM,Kpp,Kpi,Kqp,Kqi,KPLLp,KPLLi,XS,s0,H,KDG,KIM},其余参数采用典型值。设t=5 s 时母线A1处发生三相短路故障,通过调整接地电阻使得母线A2电压跌落10.5%Un,故障持续0.2 s后消失,系统恢复至原状态。由式(A1)—(A3)可得此时的λeq=0.997 7,iqLVRT.eq=0.034 0 p.u.,idmax.eq=1.2037 p.u.。
仿真得到该故障下母线A2处的有功功率及无功功率受扰轨迹,以此为基准,采用曲线拟合方法辨识待辨识参数。曲线拟合采用综合粒子群优化算法,其中,初始粒子数和学习因子分别为10 和2,最大迭代次数为200。针对粒子群优化算法易进入局部极值点的问题,本文按Logistic 函数实现非线性动态递减惯性权重,以防止算法收敛到局部极值点。具体为:
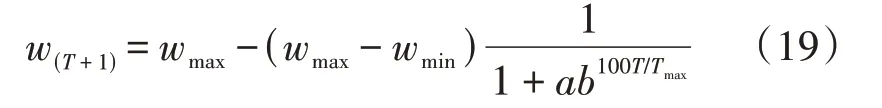
式中:w(T+1)为第T+1 次迭代的权重,T为迭代次数;Tmax为最大迭代次数;wmax、wmin分别为权重最大值、最小值;a和b为控制因子,当a=42 和b=0.77 时算法性能较好。当进行参数辨识时,等值模型中综合负荷和分布式新能源机组的初值为详细模型参数的加权平均值。
参数辨识的目标为:
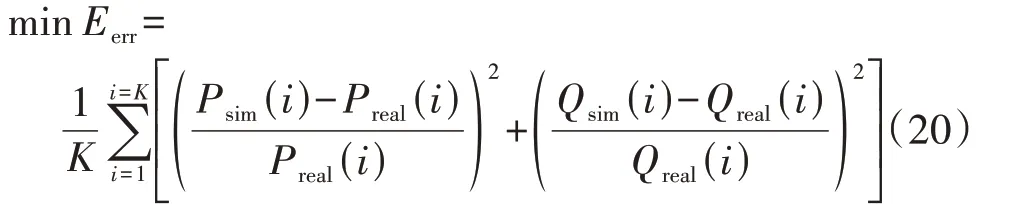
式中:Eerr为误差;P、Q分别为母线A2处的有功、无功功率,下标sim 和real分别表示基于等值模型的仿真结果以及基于详细模型的仿真结果;K为受扰轨线时间窗口内的总采样点数,采样步长为10-5s。参数辨识结果见表1,表中RDG、XDG、RCLM、XCLM、XS的辨识值为标幺值。
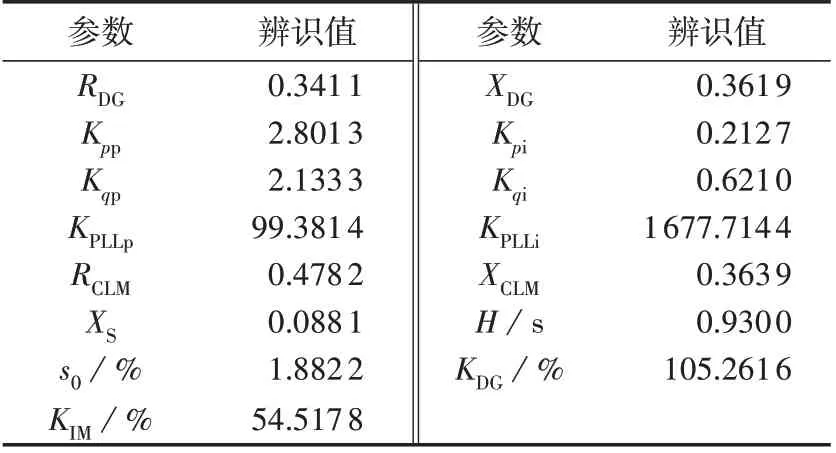
表1 参数辨识结果Table 1 Results of parameter identification
当母线A2电压跌落10.5%Un时,详细模型和基于表1 参数的等值模型在等值母线A2处有功功率P、无功功率Q、等值电压Ueq、a相瞬时电压ua和瞬时电流ia的受扰轨迹对比情况如图6所示,图中,Ueq、ua和ia均为标幺值,后同。此时,由式(20)可计算出详细模型和等值模型的误差为0.019 5。可以看出,等值模型具有较好的拟合精度。同时,针对现有研究等值时大多未考虑分布式新能源机组LVRT 的情况,图6 给出了未考虑LVRT 时等值模型的功率响应,模型参数设置与表1 相同,此时详细模型和未考虑LVRT 等值模型的误差为0.020 9。可以看出,考虑LVRT的等值模型具有更好的拟合精度。
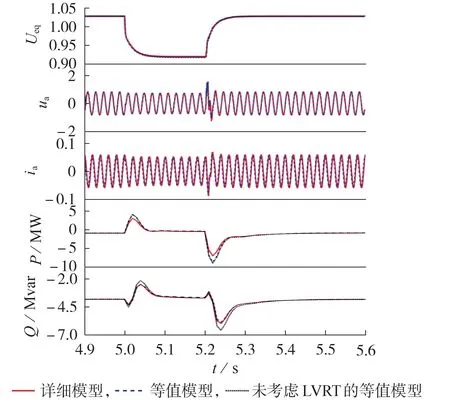
图6 电压跌落10.5%Un时详细模型和等值模型受扰轨迹Fig.6 Disturbed trajectories of equivalent model and detail model under 10.5%Un voltage dip
上述扰动下,只有部分分布式新能源机组进入LVRT,为进一步验证所有分布式新能源机组都进入LVRT 时的模型适应性,设置新的扰动为t=5 s 时母线A1处发生三相短路故障,通过调整接地电阻使得母线A2电压跌落了30%Un,故障持续0.2 s 后消失,系统恢复至原状态。
由式(A1)—(A3)求得此时非线性环节参数分别为λeq=0.775,iqLVRT.eq=0.174 p.u.,idmax.eq=1.203 7 p.u.。该扰动下,详细模型和基于表1 参数的等值模型在等值母线A2处有功功率P、无功功率Q、等值电压Ueq、a 相瞬时电压ua和瞬时电流ia的受扰轨迹对比情况如附录A 图A8所示。此时,详细模型与等值模型及不考虑LVRT 的等值模型的误差分别为0.028 2和0.057 7。由图可知,当所有分布式新能源机组都进入LVRT 状态后等值模型也具有较高的等值精度;当不考虑LVRT 等值时,其等值模型随着分布式新能源机组进入LVRT 状态的数目增多,LVRT 出力逐步增大,拟合误差逐渐增大。
4.3 不对称电压跌落时等值模型的适应性分析
上述仿真验证了网侧对称故障下等值模型的精度,下面进一步分析网侧不对称故障下等值方法的适应性。新的扰动设置为t=5 s 时母线A1处发生ab 两相短路故障,且其电压皆跌落50%Un,故障持续0.2 s 后消失,系统恢复至原状态。由式(A1)—(A3)可得此时非线性环节参数分别为λeq=0.809 5,iqLVRT.eq=0.159 3 p.u.,idmax.eq=1.203 7 p.u.。该扰动下,详细模型和基于表1参数的等值模型在等值母线A2处有功功率P、无功功率Q、等值电压Ueq、a相瞬时电压ua和瞬时电流ia的受扰轨迹对比情况如附录A图A9所示。此时2 个模型间的误差为0.167 2。由图可知,不对称故障下等值模型仍具有较好的等值精度,但是相比于对称故障,其等值误差有了一定程度的提高,该现象是由系统不对称故障下产生的谐波所造成的。
5 结论
本文基于PSCAD/EMTDC 平台推荐的分布式新能源机组的详细模型,研究了DFIG、DDPMSG 以及PV 非线性环节的等值建模方法。针对配电网中分布式新能源机组的地理位置不同、LVRT控制策略差异导致其非线性环节运行状态的差异,分析了等值模型中低电压有功调整系数、无功附加电流以及电流限幅值与等值母线电压跌落程度的关系,得到了近似表达各非线性环节的非机理模型。算例仿真表明所提模型具有较好的适应性。
将所建多类型分布式新能源机组通用模型与传统综合负荷并联作为主动配电网的等值模型。以某实际主动配电网为例,发现当网侧发生对称故障时,建立的模型能较好地描述计及LVRT 时,含多类型分布式新能源机组主动配电网的动态特性;当网侧发生不对称故障时,等值模型的拟合精度较好,但对不对称故障下谐波的拟合精度不高。
本文所采用的DFIG、DDPMSG 以及PV 模型基于PSCAD/EMTDC 平台的推荐模型结构及参数,但所提建模方法也适用于分布式新能源机组的其他模型结构或参数。
本文的创新点在于针对主动配电网中分布式新能源机组种类较多、位置较分散的问题,提出了多类型分布式新能源机组的等值建模方法,尤其是给出了非线性环节的等值建模方法。后续将针对主动配电网中电子电子化负荷,研究含高比例电力电子装备的主动配电网等值建模方法。
附录见本刊网络版(http://www.epae.cn)。
